一種基于高階梯度理論的微構件力學尺度效應模型*

，，，

(廣東工貿職業技術學院機械工程系，廣東廣州 510510)

一種基于高階梯度理論的微構件力學尺度效應模型*

原波，丘永亮，何顯運，徐勇軍

(廣東工貿職業技術學院機械工程系，廣東廣州 510510)

實驗發現微構件的力學性能存在尺度效應，傳統力學模型無法解釋這一現象。該論文基于高階應變梯度理論構建了一種針對微構件在三點彎曲實驗中的彈性性能的尺度效應模型，該模型包含一個與材料自身相關的一個參數，可以解釋微構件在實驗過程中彈性力學性能的尺度效應。通過對比該理論模型與已有模型之間的關系，分析了模型的適用性。

微構件，尺度效應，高階梯度理論

1 引言

許多針對微構件的力學實驗證實，其力學性能會隨著其特征尺寸的減小而發生顯著變化[1]。由于經典力學中不存在材料尺度參量，因此無法解釋微構件力學性能的尺度效應，在經典力學的基礎上進一步發展包含材料尺度參量的高階應變梯度理論，有望為微構件的力學研究提供新思路。有研究指出，微構件的尺度效應可能是由材料內部的非局部效應導致。該方面的開創性工作可以追溯到由Toupin 和 Mindlin 等人建立的非局部應變梯度理論模型[2]，Fleck 和 Hutchinson等人對該模型做了進一步完善，簡化了模型尺度參數[3]。Yang 等人進一步簡化了Fleck 和 Hutchinson 的理論模型，并建立了各向同性介質材料的應變梯度線彈性力學模型[4]。Lam 等人又提出了針對環氧樹脂懸臂梁彎曲變形的高階應變彈性理論模型[5]。本論文利用最小勢能原理，基于Toupin 和 Mindlin的高階應變梯度理論(High order strain gradient，HSGE)構建了一種新的非局部理論模型，該模型包含一個與材料自身相關的一個參數，可以解釋微構件在實驗過程中彈性力學性能的尺度效應。

2 理論模型

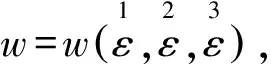
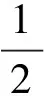
+b1φiijjφkkll+b2φijkkφijll+b3φiijkφjkll+b4φiijkφllkj+b5φiijkφlljk+b6φijklφijkl+b7φijklφjkli

+c1εiiφjjkk+c2εijφijkk+c3εijφkkjj+b0φiijj

(1)

其中：λ和μ為拉梅常數，an，bn和cn(n=1，2，3，…)為 HSGE 模型中的常數，詳見Toupin和 Mindlin的模型[2，6-7]。εij、ηijk和φijkl(i，j，k，l=x，y，z)分別表示一階、二階和三階變形梯度的分量。

在載荷q(x)的作用下，圖1所示的微結構纖維的位移分量可以表示為：

u≈-z?w(x)/?x，v=0，w=w(x)

(2)

其中：u、v和w分別表示位移矢量u在x、y和z方向的分量。可以計算出變形梯度一階、二階和三階分量中非零項為：

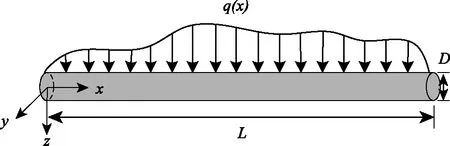
圖1 微結構纖維在外載荷作用下的彎曲示意圖Fig.1 Schematic for general bending test ofmicrofiber under external force

(3)

將式(3)代入式(1)中，對整個微結構纖維進行體積積分，可以得到應變能U的表達式為：

(4)

引入如下的關系式(5)：

(5)

其中E和v分別表示微結構材料的楊氏模量及泊松比，式(4)可以表示為：

(6)

其中I和A分別為材料的慣性矩和橫截面積。

如圖1所示，外載荷的外力功可以表示為：

(7)

受力微結構纖維的總勢能可以表示為：

∏ =U-W

(8)

根據最小勢能原理δ∏=0，通過變分計算可以得到如下的平衡方程：

(9)

研究如圖2所示的兩端固支微結構受力模型，對于直徑為D，長度為L的桿狀纖維結構，在中部集中載荷 的作用下，利用邊界條件，可以得到式(9)的解為：

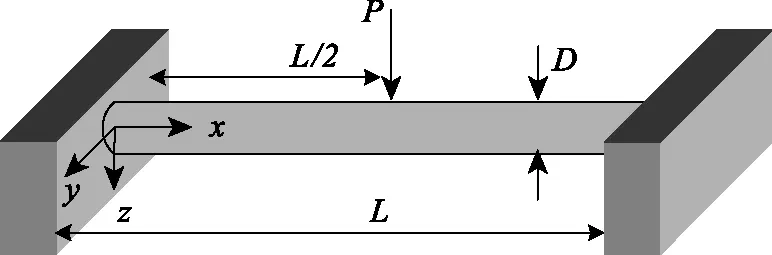
圖2 兩端固支單根微結構在集中載荷作用下的彎曲示意圖Fig.2 Coordinate system for a single-strandmicro-structure loaded in three-point bendingby external force

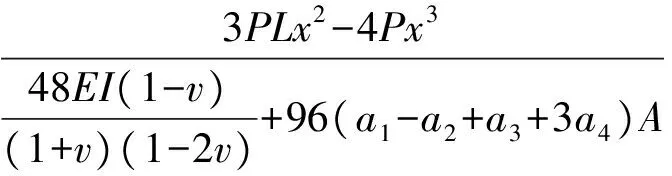
(10)

從表達式(10)中可以看出，纖維位移量的計算結果與材料參數an(n=1，2，3，4)有關，如果忽略材料內部非均勻效應的影響，則材料參數均為零，表達式回歸為：

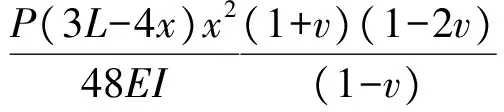
(11)

式(11)即為經典力學體系中歐拉-伯努利梁在三點彎曲變形條件下的理論解。材料的最大變形量發生在中部，即x=L/2處。忽略泊松效應，則材料的最大變形量表示為：

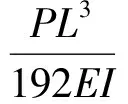
(12)

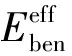
(13)

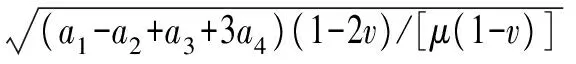
(14)

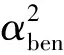
3 總結

為了解釋微結構在三點彎曲變形中所存在的尺度效應，基于HSGE理論建立了一種尺度效應模型。通過該模型可以計算出材料在彎曲變形中的尺度效應。

[1] Lim C T，Tan E P S，Ng S Y. Effects of crystalline morphology on the tensile properties of electrospun polymer nanofibers[J]. Applied Physics Letters. 2008，92(14)：141908.

[2] Mindlin R D. Second gradient of strain and surface tension in linear elasticity[J]. International Journal of Solids and Structures. 1965，1：417-438.

[3] Fleck N A，Hutchinson J W. A reformulation of strain gradient plasticity[J]. Journal of the Mechanics and Physics of Solids. 2001，49(10)：2245-2271.

[4] Yang F，Chong A C M，Lam D C C，et al. Couple stress based strain gradient theory for elasticity[J]. International Journal of Solids and Structures. 2002，39(10)：2731-2743.

[5] Lam D C C，Yang F，Chong A C M，et al. Experiments and Theory in Strain Gradient Elasticity[J]. Journal of the Mechanics and Physics of Solids. 2003，51(8)：1477-1508.

ASizeEffectModelforMicro-componentBasedonHighOrderStrainGradientTheory

YUAN Bo，QIU Yong-liang，HE Xian-yun，XU Yong-jun

(Department of Mechanical Engineering，Guangdong Polytechnic of Industry & Commerce，Guangzhou 510510，Guangdong，China)

Size effect has been observed from the mechanical testing of micro-components，classical mechanical model cannot be used to explain this phenomenon. In this paper，a model based on high order strain gradient (HSGE) theory is constructed to predict the bending size dependence of the elastic property of microfibers under three-point tests. The model contains a length scale material parameter and can be applied to explain the size dependency in bending test for micro-components. The applicability of the model was analyzed by comparing with published model.

micro-component，size effect，high order strain gradient

廣東省高等職業院校珠江學者崗位計劃資助項目(2016)；國家自然科學基金項目(No.51202069)

TQ 317.3