組合梁橋徐變分析的超級單元法

許德勝

（上海同豪土木工程咨詢有限公司，上海市 200092）

組合梁橋徐變分析的超級單元法

許德勝

（上海同豪土木工程咨詢有限公司，上海市 200092）

基于多軸應力狀態下的粘彈性本構關系，提出了鋼-混凝土組合梁橋徐變分析的超級元法。采用廣義Maxwell模型描述混凝土徐變行為，利用超級元法縮減分析規模，并通過Newton-Raphson迭代方法求解結構徐變響應。以兩跨鋼-混凝土連續梁橋為例分析了徐變對結構的影響，可供相關工程設計和實踐參考。

徐變；組合梁橋；粘彈性；超級單元；廣義Maxwell模型

0 引言

鋼-混凝土組合梁橋充分發揮了鋼、混凝土兩種材料的受力性能，已在橋梁工程中得到廣泛應用。混凝土徐變會使組合梁撓度隨時間不斷增大，并導致鋼梁與混凝土板間的應力重分布，對鋼-混凝土組合梁橋的徐變進行研究具有重要意義。

徐變效應的準確預測依賴于對徐變機理的準確描述。Ichinose等和Guedes等采用Kelvin粘彈性模型對軸壓狀態下混凝土徐變做了研究[1,2]。Diab等和Jo等分別基于廣義Maxwell粘彈性模型研究了混凝土的長期性能[3,4]。Kwak等基于應變協調條件，采用Dirichlet級數表達的徐變模型研究了組合梁橋的徐變響應[5]。程曉東等采用三參數粘彈性模型分析了鋼-混凝土組合梁橋的徐變效應[6]。需要指出，Kelvin模型不能考慮混凝土的瞬時變形，而Maxwell模型不能模擬其長期變形。可同時考慮混凝土瞬時和長期變形的最簡單模型為三參數模型和線性固體模型，但該類模型因采用單一松弛時間，在混凝土的整個徐變時間內與實驗數據吻合的能力并不好[7]。此外，多數研究[1-5]都基于單軸應力狀態下的粘彈性本構關系，無法考慮混凝土的三維應力狀態。基于廣義Maxwell粘彈性模型，采用實體單元分析可在理論上克服上述缺陷，但考慮到龐大的計算量，難以在實際工程中應用。

本文基于三維粘彈性理論，采用廣義Maxwell模型，構造了考慮混凝土徐變的超級元模型，并將該模型用于兩跨鋼-混凝土組合梁橋的徐變分析。

1 混凝土徐變的增量本構關系

本文采用廣義Maxwell模型模擬混凝土徐變，見圖1。其中，每個支路可采用長短不同的松弛時間，以準確模擬混凝土的徐變歷程。根據應力松弛試驗下的Laplace變換和Laplace逆變換可得單軸應力狀態下的松弛模量，

圖1 廣義Maxwell模型

式中：τi=ηi/ki為第i個支路的松弛時間。

利用Boltzmann疊加原理，由式（1）可得單軸應力狀態下混凝土的積分型本構關系：

考慮到Laplace變換只影響時間參數，可將上面的本構關系直接推廣到多軸應力狀態：

式中：Sij和eij為應力偏量和應變偏量；σm和εm為平均應力和平均應變；Gi和Ki為剪切模量和體積模量相關的材料常數，可根據試驗或規范給出的徐變系數確定。

將式（3）的時間變量進行離散，記時間分點為0=t0＜t1＜tn＜tn+1＜…，為求算由整個應變歷史所描述的積分項，可由前一時刻tn的解答遞推得到當前時刻tn+1的解答[8]。此時，需要將混凝土多軸應力狀態下的本構關系表達為增量形式，即

式中：時間步長Δtn=tn+1-tn。

2 考慮徐變的超級單元列式

為縮減組合梁橋徐變分析的空間離散規模，本文將述模型引入基于二次等參映射方法和非協調元理論構造的超級單元。

超級單元有八個節點，并可以含有多個積分子域，不同子域代表不同的材料或構件。單元子域的局部坐標系見圖2。

則局部坐標系和整體坐標系下的位移轉換矩陣可表達為：

式中：lx′，mx′，nx′分別為 x′軸與整體坐標軸x,y,z的夾角余弦，其余符號含義相似。

記單元內任意點的整體坐標為x={x,y,z}T，對應的自然坐標為ξ={ξ，n，ζ}T，在子域對應的母單元中的坐標為ξ′={ξ′，η′，ζ′}T，則 x 與ξ間的等參變換可定義為初次等參變換，ξ與ξ′間的變換為第二次等參變換，見圖3。

圖3 超級單元等參映射

則存在：

為改善超級元各子域的變形并采用完全三維的本構關系，為每個子域局部坐標系下的位移分量附加下述非協調位移[9]：

利用式（5）將式（7）中局部坐標系下的位移轉換到整體坐標系中，可得第k個子域的切線剛度矩陣：

式中：m為超級元所包含的子域數。

將式（9）中的單元剛度矩陣組集，可得整個離散系統的切線剛度矩陣KT，用Newton-Raphson法求解混凝土徐變這類非線性問題時可采用下述迭代格式：

式中：k=0，1，2，…，上標（k）表示第 k 個迭代步對應的物理量；F為外力等效節點力為第k個迭代步的內力等效節點力。式（10a）的右端代表殘差，表征迭代過程中的不平衡量，可作為迭代收斂的依據。

3 鋼-混凝土組合梁橋的徐變分析

本節將利用Kwak等的兩跨鋼-混凝土組合梁，闡述超級元法在鋼-混凝土組合梁橋徐變分析中的應用。

鋼-混凝土組合梁橋的幾何尺寸見圖4，荷載q由表1中各項荷載分量確定。

圖4 兩跨連續組合梁橋 (單位：cm)

表1 組合梁橋荷載條件 kN/m

組合梁橋的材料性質參數取值見表2，考慮到Kwak等分析時采用了ACI徐變模型，本文采用4個Maxwell支路對ACI模型的徐變系數進行非線性最小二乘擬合，確定的模型參數見表3。為便于分析，將鋼材視為各Maxwell支路的剪切模量和體積模量均為零的特殊粘彈性材料。

表2 組合梁橋材料性質參數

表3 廣義Maxwell模型材料參數

將圖4中的連續梁在縱向每2 m劃分1個單元，在橫向劃分2個單元，見圖5。其中，混凝土板采用僅含1個子域的超級元劃分；工字鋼梁采用含有5個子域的超級元劃分，但其中2個空子域不參與剛度矩陣計算。整個系統共劃分了40個單元和126個節點(含虛擬節點)。徐變分析中，取等時間步長1.0 d，計算開始加載后1 000 d內混凝土徐變效應。為考查本文方法的計算精度，還采用ABAQUS程序分析了該問題。需要指出，為能夠準確描述鋼-混凝土組合截面的幾何形狀，采用ABAQUS三維實體單元分析時至少需劃分504個節點和240個單元。

圖5 有限元網格

表4 跨中（x=10 m）測點A撓度 mm

表4給出了不同時間跨中位置測點A的撓度變化。不難看出，超級元法僅需1/4的系統自由度即可獲得與ABAQUS程序接近的解答（誤差3%以內），證實了本文方法的可靠性和有效性。

圖6給出了不同齡期沿梁軸線x方向的撓度變化；因未考慮混凝土的收縮變形，撓度計算值要比Kwak等的解答略小。圖7為混凝土徐變導致的跨中位置B、C測點的軸向應力變化。徐變引起鋼-混凝土間的應力重分布，導致鋼梁應力增長和混凝土板應力下降。

圖6 撓度隨時間的變化

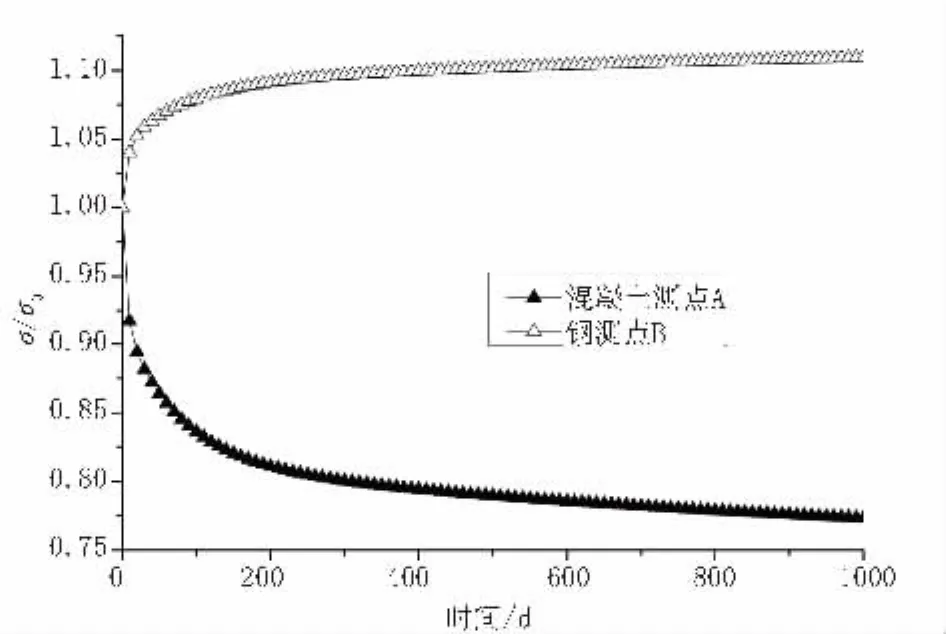
圖7 軸向應力隨時間的變化

4 結論

（1）本文基于三維粘彈性理論，采用廣義Maxwell模型考慮混凝土的徐變特性。相對于具有單一松弛時間的粘彈性模型，廣義Maxwell模型可以更好地反映混凝土的徐變規律。

（2）超級元法允許單個單元內含有不同的材料和構件，縮減了徐變分析中空間離散所需的計算量，提高了計算效率。

（3）類似于對ACI徐變模型的模擬，可采用廣義Maxwell模型對《預應力混凝土橋涵設計規范》(JTG D62-2004)給出的混凝土徐變系數進行非線性最小二乘擬合，使本文方法可直接按04規范要求分析混凝土橋梁的徐變效應。進一步研究表明，通常僅需3-4個Maxwell支路即可很好地擬合04規范給出的徐變系數。

[1]Ichinose L H,Watanabe E,Nakai H.An experimental study on creep of concrete filled steel pipes[J].Journal of Constructional Steel Research,2001,57(4):453-466.

[2]Guedes R M,Tavares C M L,Ferreira A J M.Experimental and theoretical study of the creep behavior of GFRP-reinforced polymer concrete [J].Composites Science and Technology,2004,64(9):1251-1259.

[3]Diab H,Wu Z.A linear viscoelastic model for interfacial long-term behavior of FRP-concrete interface[J].Composites,Part B:Engineering,2008,39(4):722-730.

[4]Jo B W,Tae G H,Kim C H.Uniaxial creep behavior and prediction of recycled-PET polymer concrete[J].Construction and Building Materials,2007,21(7):1552-1559.

[5]Kwak H G,Seo Y J.Long-term behavior of composite girder bridges[J].Computers&Structures,2000(74):583-599.

[6]Cheng X D,Cheng L S,Ye G R.Creep Analysis of steel-concrete compositegirderbridgesbythemethod 3D-VLE[J].Chinese Journal of Computational Mechanics,2006,23(4):470-475.

[7]Roylance D.Engineering viscoelasticity[M].Massachusetts Institute of Technology Cambridge,2001.

[8]Zenkiewicz O C,Taylor R L.The finite element method[M].McGraw-Hill,New York,2005.

[9]許德勝,凌道盛,肖汝誠,等.八節點非協調實體板單元[J].計算力學學報,2009,26(2):264-269.

U442

A

1009-7716（2017）12-0040-04

10.16799/j.cnki.csdqyfh.2017.12.012

2017-06-30

許德勝(1979-)，男，山東東營人，工程師，從事橋梁結構分析理論研究與結構分析軟件研發工作。