大壩監(jiān)測(cè)數(shù)據(jù)多重共線性問題處理方法的比較研究
丁立,錢強(qiáng)強(qiáng),趙俊,吳建曄
(湖州市測(cè)繪院,浙江 湖州 313000)
大壩監(jiān)測(cè)數(shù)據(jù)多重共線性問題處理方法的比較研究
丁立*,錢強(qiáng)強(qiáng),趙俊,吳建曄
(湖州市測(cè)繪院,浙江 湖州 313000)
多重共線性是大壩安全監(jiān)測(cè)中一種常見的病態(tài)數(shù)據(jù)問題,為了削弱其對(duì)參數(shù)估計(jì)的影響,本文綜合應(yīng)用了主成分回歸法、偏最小二乘回歸法、嶺回歸法和Lasso法等四種有偏估計(jì)方法對(duì)大壩實(shí)測(cè)數(shù)據(jù)進(jìn)行建模分析,并與多元線性回歸模型結(jié)果進(jìn)行比較。結(jié)果表明,多重共線性對(duì)模型的擬合及預(yù)報(bào)效果影響不大,但在模型的可解釋性以及模型系數(shù)的穩(wěn)定性方面,有偏估計(jì)方法更具優(yōu)越性,且四種有偏估計(jì)方法針對(duì)多重共線性數(shù)據(jù)建模各有其特點(diǎn)。
多重共線性;主成分回歸法;偏最小二乘回歸法;嶺回歸法;Lasso法
1 引 言
多重共線性是指在自變量之間存在線性相關(guān)關(guān)系的現(xiàn)象,它的存在會(huì)影響最小二乘回歸模型的參數(shù)估計(jì),降低回歸模型的可靠性,導(dǎo)致模型不能反映大壩的真實(shí)狀態(tài)。為了削弱多重共線性對(duì)參數(shù)估計(jì)的影響,研究人員分別從子集選擇、系數(shù)壓縮以及變量重組等角度對(duì)參數(shù)估計(jì)方法進(jìn)行了改進(jìn)研究。其中子集選擇法的代表方法主要是逐步回歸法,而收縮法和降維法本質(zhì)上都屬于有偏估計(jì)方法,有偏估計(jì)方法在均方誤差意義下對(duì)最小二乘估計(jì)具有改良作用,主要體現(xiàn)在參數(shù)估計(jì)值更為準(zhǔn)確穩(wěn)定[1~2]。經(jīng)過長(zhǎng)時(shí)間的不斷開拓,以嶺回歸、偏最小二乘回歸、主成分回歸和Lasso法為代表的有偏估計(jì)法已被應(yīng)用于不同研究領(lǐng)域。目前,處理大壩安全監(jiān)測(cè)數(shù)據(jù)中多重共線性問題的有偏估計(jì)方法相對(duì)單一,大部分的研究主要考察單一方法的應(yīng)用效果,對(duì)原理相近的幾種方法的應(yīng)用效果進(jìn)行對(duì)比分析研究相對(duì)較少,因此,本文綜合采用多種有偏估計(jì)方法建立大壩位移監(jiān)控模型,通過實(shí)例比較各種方法的特點(diǎn)并分析其相對(duì)于最小二乘估計(jì)的優(yōu)越性。
2 多重共線性及其處理方法
對(duì)于由單個(gè)因變量Y和n個(gè)自變量X1,X2,…,Xn構(gòu)成的線性回歸模型
Y=β1X1+β2X2+…+βnXn+ε
(1)
式中β1,β2,…,βn是未知參數(shù),ε是隨機(jī)誤差項(xiàng)。
如果存在一組不全為0的常數(shù)α1,α2,…,αn使得式(2)成立
α1X1+α2X2+…+αnXn≈0
(2)
那么就稱變量X1,X2,…,Xn之間存在多重共線性。
當(dāng)變量間存在嚴(yán)重的多重共線性時(shí),如果仍采用最小二乘法進(jìn)行參數(shù)估計(jì),可能引起法方程的解極不穩(wěn)定,主要表現(xiàn)為,法方程中的系數(shù)或常數(shù)項(xiàng)存在舍入誤差而產(chǎn)生微小變化時(shí),會(huì)引起參數(shù)解的差異很大。
有偏估計(jì)能夠有效地處理多元線性回歸模型中的多重共線性問題。目前,處理多重共線性的常用方法有主成分回歸法[3]、偏最小二乘回歸法[4,5]、嶺回歸法和Lasso法[6],表1中介紹了這四種方法的基本思想以及優(yōu)缺點(diǎn)。四種方法的建模步驟及算法在其他相關(guān)文獻(xiàn)中均有詳細(xì)介紹,本文在此不再贅述。
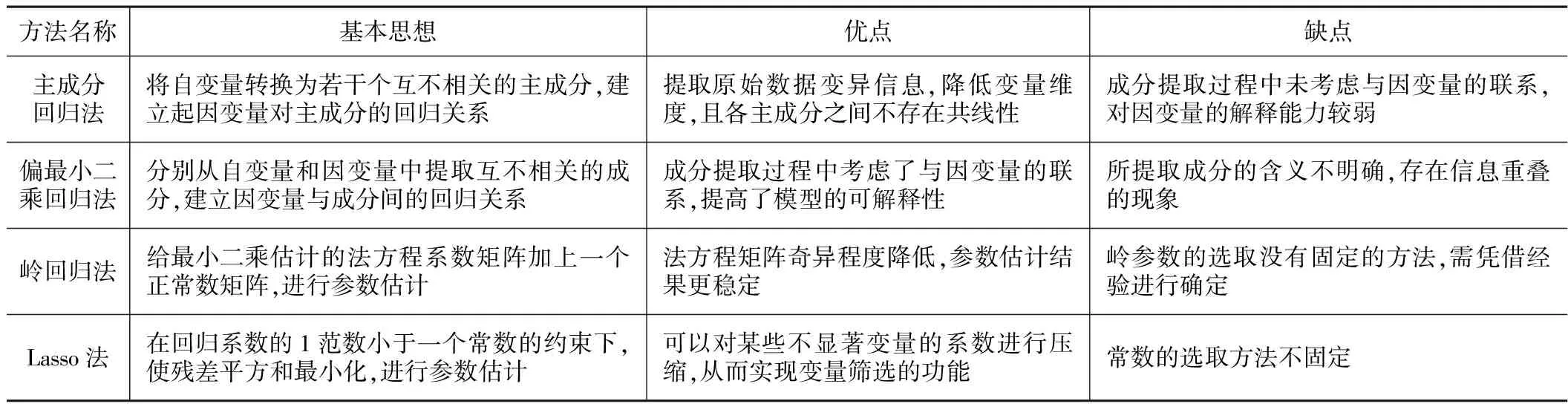
四種有偏估計(jì)方法的對(duì)比 表1
3 實(shí)例分析
為了說(shuō)明在變量間存在嚴(yán)重多重共線性問題時(shí)最小二乘估計(jì)的不適用性以及比較四種有偏估計(jì)方法的效果,以某混凝土壩一壩段135期監(jiān)測(cè)數(shù)據(jù)為例,分別建立位移監(jiān)控模型。根據(jù)實(shí)測(cè)資料,確定大壩位移初選統(tǒng)計(jì)模型的表達(dá)式為:
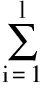
(3)
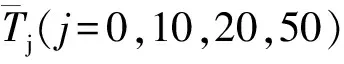
從135期大壩實(shí)測(cè)數(shù)據(jù)中取出前125期數(shù)據(jù)建立大壩位移y與水位因子、溫度因子和時(shí)效因子之間的多元線性回歸模型,按照逐步回歸的步驟引進(jìn)顯著變量,剔除不顯著變量,最終建立的模型為:
y=-353.6097H+1.3572H2-0.0017H3+0.0257T20
-0.1956T1s-0.0989T2s+0.0324T3s-1.0982θ
+0.2026lnθ+30698.8738
(4)
經(jīng)計(jì)算,逐步回歸模型的復(fù)相關(guān)系數(shù)為0.9848,F(xiàn)檢驗(yàn)值為829.6,擬合殘差平方和為0.272,如果取顯著性水平α=0.05,該模型中所有的環(huán)境因子對(duì)位移y的影響都是顯著的。
為了進(jìn)一步驗(yàn)證逐步回歸模型中系數(shù)的穩(wěn)定性和可靠性,以下將對(duì)樣本數(shù)據(jù)進(jìn)行抽樣,然后建立不同樣本下對(duì)應(yīng)的位移逐步回歸模型,抽樣的方案共分為5種:方案一,以135期觀測(cè)數(shù)據(jù)為樣本;方案二,隔一期數(shù)據(jù)抽取一個(gè)樣本;方案三,隔兩期數(shù)據(jù)抽取一個(gè)樣本;方案四,隔三期數(shù)據(jù)抽取一個(gè)樣本;方案五,隔四期數(shù)據(jù)抽取一個(gè)樣本。五種抽樣方案對(duì)應(yīng)的逐步回歸模型系數(shù)如表2所示。
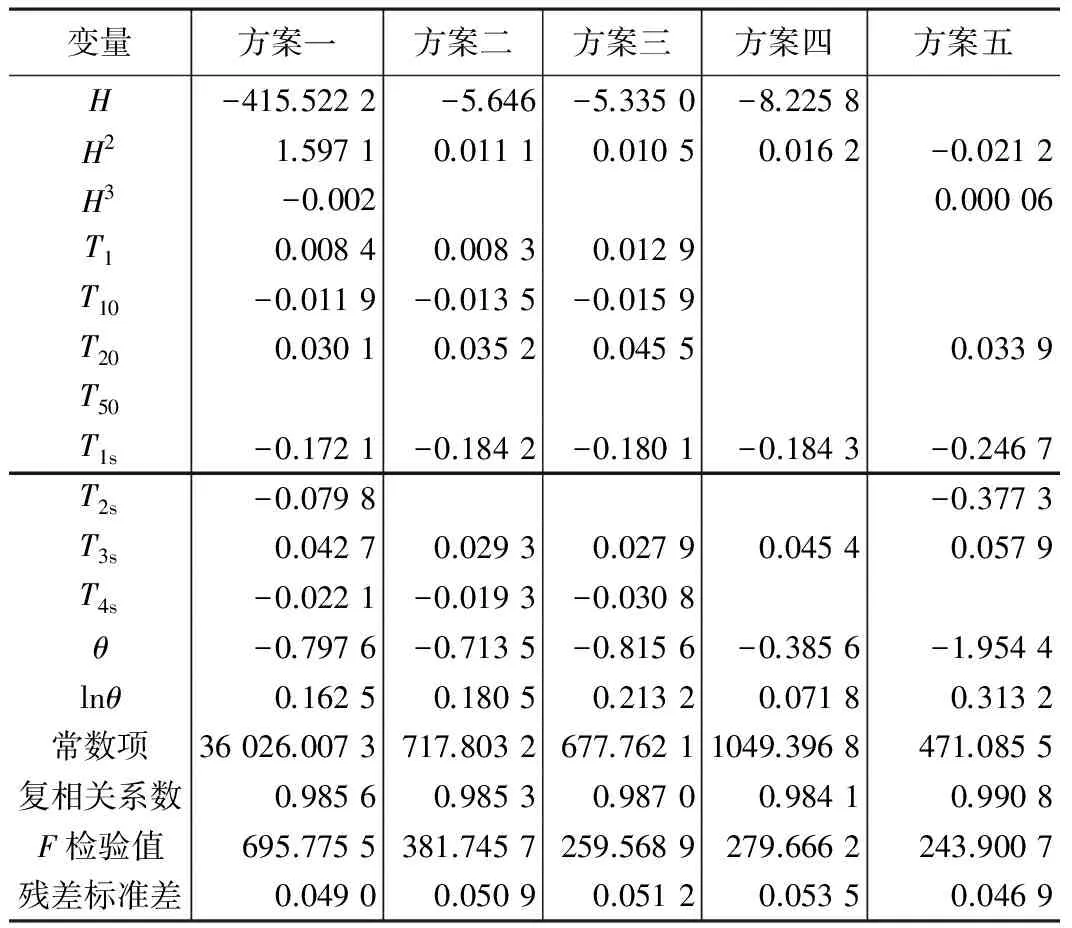
不同抽樣方案對(duì)應(yīng)的位移逐步回歸模型系數(shù) 表2
同樣采用大壩實(shí)測(cè)數(shù)據(jù)中前125期數(shù)據(jù),分別采用四種有偏估計(jì)方法建立大壩位移回歸模型。
在采用主成分回歸法建模時(shí),以主成分的累計(jì)貢獻(xiàn)率達(dá)到95%為標(biāo)準(zhǔn),共提取了3個(gè)主成分,各自的貢獻(xiàn)率分別為61.51%、32.86%和1.97%,其累計(jì)貢獻(xiàn)率達(dá)到96.34%,根據(jù)提取結(jié)果建立3個(gè)主成分對(duì)位移的回歸模型:
y=0.04704H+9.086×10-5H2+2.339×10-7H3
+0.00241T1+5.587×10-4T10+0.00176T20
+0.00592T50-0.05639T1s+0.04222T2s
-0.00766T3s-0.00258T4s-0.01633θ
-0.03479lnθ-19.39277
(5)
y=0.02981H+5.851×10-5H2+1.531×10-7H3
-0.00197T1-0.01094T10+0.01081T20
+0.01734T50-0.15491T1s+0.15429T2s
+0.00925T3s-0.00098T4s+0.04708θ
+0.03091lnθ-12.26631
(6)
在采用嶺回歸法建模時(shí),選用L-曲線法確定嶺參數(shù),根據(jù)L-曲線法原理,當(dāng)k=0.335時(shí),可確定曲率最大點(diǎn),因而k=0.335即為使用L-曲線法確定的嶺參數(shù),然后計(jì)算大壩位移嶺回歸模型為:
y=0.02729H+6.066×10-5H2+1.767×10-7H3
+0.00625T1-0.01657T10+0.02872T20
+0.01434T50-0.16295T1s+0.0954T2s
+0.00568T3s-0.01295T4s-0.36983θ
+0.13112lnθ-11.27464
(7)
在采用Lasso法建立大壩位移監(jiān)控模型時(shí),按照最小角回歸算法(LARS)[7]求解Lasso問題,根據(jù)交叉檢驗(yàn)法來(lái)確定懲罰參數(shù)t,當(dāng)t=38.0166時(shí),即算法進(jìn)行到第18步時(shí),CV=0.2965,取得最小值,其對(duì)應(yīng)的估計(jì)參數(shù)即為選出的Lasso法最優(yōu)解,因此Lasso法確定的大壩位移模型為:
y=0.04571H+9.38×10-5H2+0.00548T1
-0.01601T10+0.02549T20+0.01423T50
-0.15819T1s+0.1091T2s+0.00591T3s
-0.01181T4s-0.26741θ+0.10891lnθ
-15.42662
(8)
為了進(jìn)一步比較各種方法所建大壩位移模型的預(yù)報(bào)效果,利用后10期數(shù)據(jù)進(jìn)行預(yù)報(bào),預(yù)報(bào)結(jié)果如表3所示。
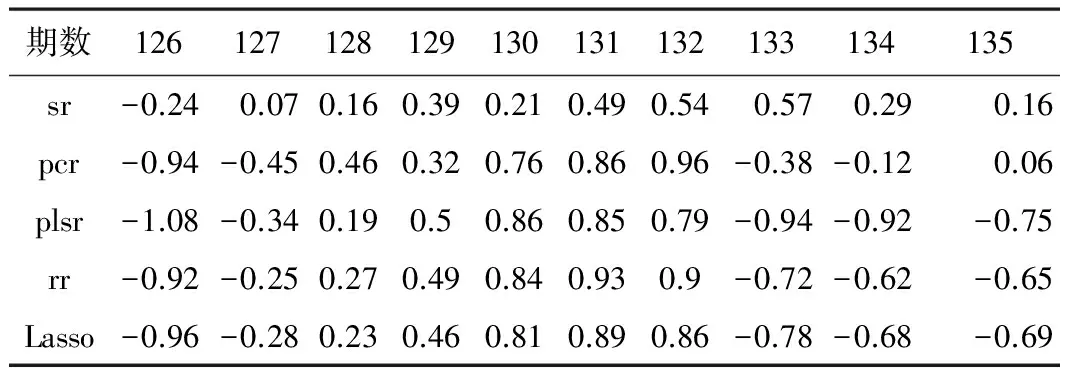
5種模型的預(yù)報(bào)結(jié)果(單位/mm) 表3
(注:sr:逐步回歸模型,pcr:主成分回歸模型,plsr:偏最小二乘回歸模型,rr:嶺回歸模型)
通過以上的計(jì)算分析不難發(fā)現(xiàn),無(wú)論是多元線性回歸法,還是四種有偏估計(jì)方法,所建立的大壩位移監(jiān)控模型都能達(dá)到令人滿意的效果,而單從數(shù)值上看,多元線性回歸法的擬合和預(yù)報(bào)效果更為理想。可見,僅將擬合及預(yù)報(bào)效果作為評(píng)價(jià)指標(biāo),多重共線性問題對(duì)最小二乘估計(jì)的影響微乎其微。
理論上,水位因子H2和H3都由H演變而來(lái),三者的變化趨勢(shì)是基本一致的,而且根據(jù)經(jīng)驗(yàn)判斷,大壩水平位移量應(yīng)該與上游水位因子呈正相關(guān)關(guān)系,因此可以判定模型中三個(gè)因子的符號(hào)都應(yīng)該為正,而在逐步回歸模型中,盡管水位因子作為混凝土壩水平位移重要的影響因子都被選入最終的模型中,但三個(gè)水位因子的符號(hào)并不一致,其中位移量與水位因子H2呈正相關(guān)關(guān)系,而與H、H3卻呈負(fù)相關(guān)關(guān)系,這顯然給模型的解釋帶來(lái)了困難。不僅如此,表2也充分說(shuō)明不同抽樣方案對(duì)應(yīng)的位移逐步回歸模型系數(shù)的穩(wěn)定性較差,在不同樣本模型中同一變量對(duì)應(yīng)的回歸系數(shù)發(fā)生了較大的波動(dòng),有些因子甚至發(fā)生了符號(hào)上的變化,而且不同抽樣方案選出的顯著因子也有所差別。通過四種有偏估計(jì)方法建立的模型的可解釋性則相對(duì)較好,水平位移量與上游水位因子均呈正相關(guān)關(guān)系,各個(gè)模型對(duì)應(yīng)系數(shù)的數(shù)量級(jí)也趨于一致,且系數(shù)的符號(hào)和大小均未發(fā)生大的波動(dòng),較為穩(wěn)定,不同抽樣方案對(duì)應(yīng)的各模型系數(shù)變化情況如圖1~圖4所示。
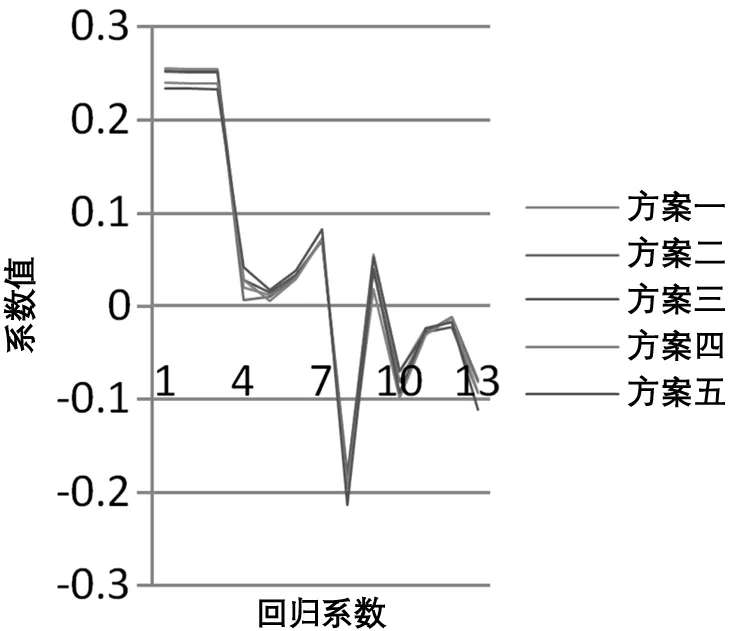
圖1 主成分回歸模型系數(shù)變化圖
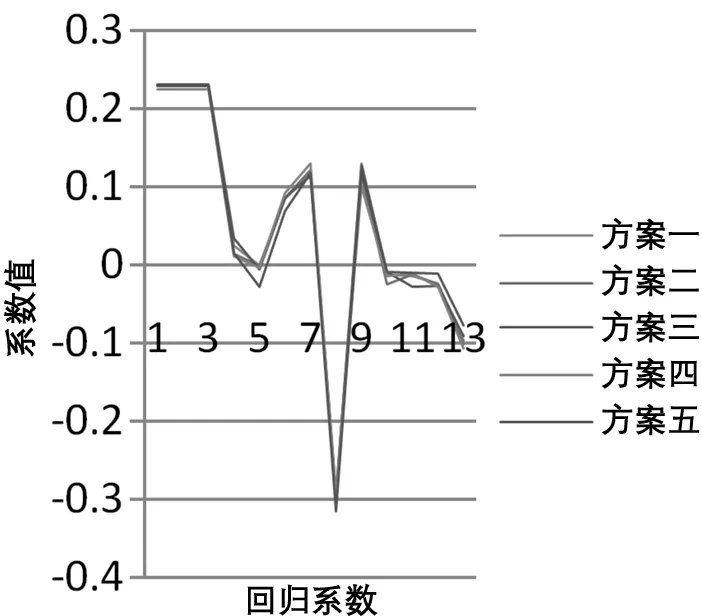
圖2 偏最小二乘回歸模型系數(shù)變化圖
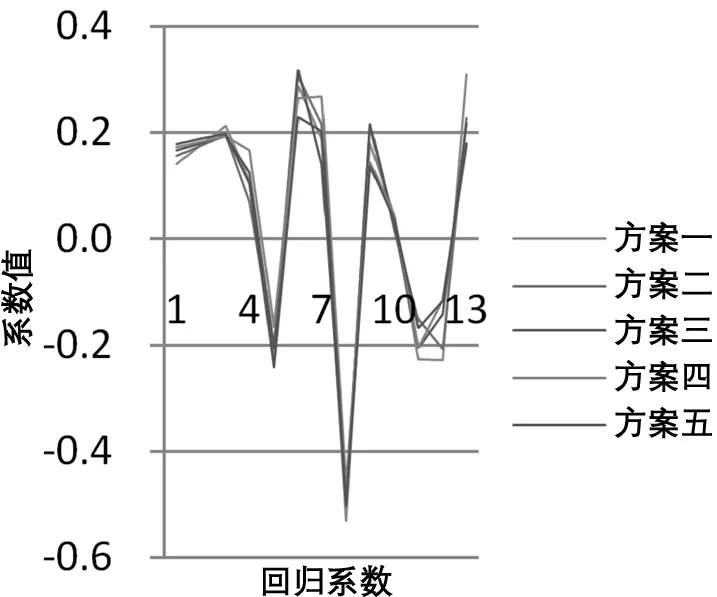
圖3 嶺回歸模型系數(shù)變化圖
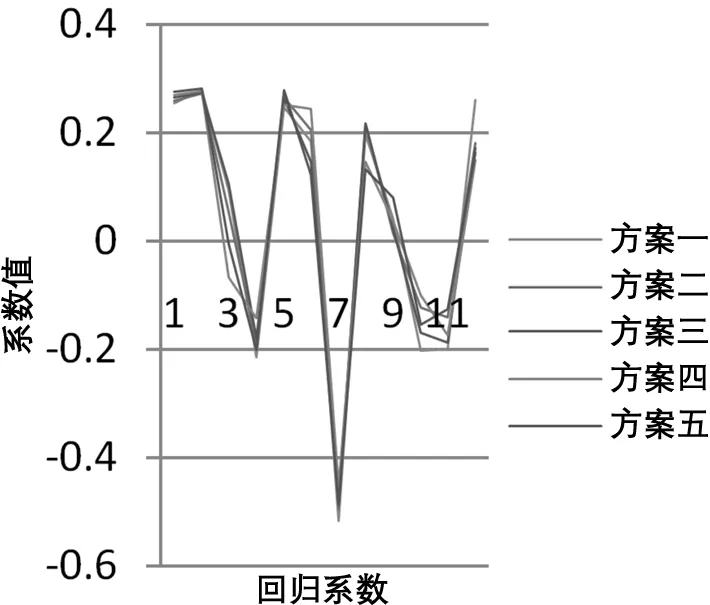
圖4 Lasso模型系數(shù)變化圖
通過圖1~圖4可以發(fā)現(xiàn),主成分回歸模型系數(shù)結(jié)構(gòu)及變化趨勢(shì)和偏最小二乘回歸模型相似,嶺回歸模型系數(shù)結(jié)構(gòu)及變化趨勢(shì)與Lasso模型相似。
根據(jù)主成分回歸法和偏最小二乘回歸法的建模思想可以得知,兩種方法都需要進(jìn)行成分提取,所提取的成分之間線性無(wú)關(guān),減弱了原始自變量間的多重共線性,最終利用所提取的成分進(jìn)行回歸處理。盡管兩種方法的思想趨近,但建模原理有本質(zhì)區(qū)別。從主成分回歸法計(jì)算過程來(lái)看,三個(gè)主成分F1、F2和F3的累計(jì)貢獻(xiàn)率達(dá)到96.34%,基本涵蓋了自變量數(shù)據(jù)中絕大部分的變異信息,但由于在成分提取過程中,因變量并未發(fā)揮任何作用,所有主成分均是利用自變量相關(guān)系數(shù)矩陣求取的,因此不能保證各主成分對(duì)因變量擁有較強(qiáng)的解釋能力。對(duì)于偏最小二乘回歸法建模而言,成分的提取與自變量、因變量都息息相關(guān),不僅要求攜帶盡可能多的原始自變量信息,而且要求每個(gè)成分與因變量的相關(guān)度盡可能大,該實(shí)例中當(dāng)提取到第四個(gè)成分時(shí),各成分對(duì)因變量的累計(jì)解釋能力達(dá)到0.9721,所以偏最小二乘回歸法提取成分的過程與主成分回歸法相比更加合理完善。結(jié)合兩者的擬合效果來(lái)看,主成分回歸模型的擬合效果明顯比偏最小二乘回歸模型差,這很大程度上是由主成分對(duì)因變量解釋能力不強(qiáng)導(dǎo)致的,從這一點(diǎn)上看,偏最小二乘模型的可解釋性更強(qiáng)且可靠性更高。
嶺回歸法與Lasso法都涉及對(duì)系數(shù)的壓縮,但兩種方法對(duì)系數(shù)的壓縮程度會(huì)存在差異,使用Lasso法建立的模型則會(huì)更加精煉、稀疏。從模型稀疏性的角度考慮,Lasso法能夠降低模型的復(fù)雜度,顯然更具優(yōu)勢(shì),但也存在不可靠之處,如果懲罰參數(shù)選取不得當(dāng),會(huì)導(dǎo)致模型過于稀疏,一些重要的自變量可能未被選入模型中。在本實(shí)例中,嶺回歸法與Lasso法都能有效地處理大壩自變量因子間的多重共線性問題,雖然擬合效果比多元線性回歸模型稍差,但所得的回歸系數(shù)更符合實(shí)際,兩種模型的系數(shù)結(jié)構(gòu)及變化趨勢(shì)較為吻合,對(duì)于不同樣本方案的模型系數(shù)穩(wěn)定性良好,而且在本實(shí)例中,使用Lasso法建立模型時(shí),并未發(fā)生模型過于稀疏的情況,較嶺回歸模型而言,僅將水位因子H3的系數(shù)壓縮為0,模型更加簡(jiǎn)潔。
4 結(jié) 語(yǔ)
本文以某混凝土大壩實(shí)測(cè)數(shù)據(jù)為例,分別采用多元線性回歸法和四種有偏估計(jì)方法進(jìn)行建模分析。本文的計(jì)算結(jié)果表明,受多重共線性的影響,多元線性回歸法的處理結(jié)果在可解釋性和系數(shù)的穩(wěn)定性方面均比四種有偏估計(jì)方法要差。通過對(duì)基本原理相似的有偏估計(jì)方法比較可知,雖然主成分回歸法和偏最小二乘回歸法都能較有效地處理多重共線性問題,但偏最小二乘回歸模型的可解釋性更強(qiáng)且可靠性更高,采用嶺回歸法和Lasso法所建模型的系數(shù)結(jié)構(gòu)及變化趨勢(shì)較為吻合,而Lasso法建立的模型更加簡(jiǎn)潔稀疏。
[1] 唐小燕. 有偏估計(jì)若干問題的研究[D]. 哈爾濱:東北林業(yè)大學(xué),2010.
[2] 歸慶明,李國(guó)重,歐吉坤. 有偏估計(jì)與LS估計(jì)的比較與選擇[J]. 測(cè)繪學(xué)報(bào),2003,32(1):26~30.
[3] 陳希孺,王松桂. 近代實(shí)用回歸分析[M]. 廣西人民出版社,1984.
[4] 付凌暉,王惠文. 多項(xiàng)式回歸的建模方法比較研究[J]. 數(shù)理統(tǒng)計(jì)與管理,2004,23(1):48~52.
[5] 王惠文,吳載斌,孟潔. 偏最小二乘回歸的線性與非線性方法[M]. 國(guó)防工業(yè)出版社,2006.
[6] 張燕,宋俊峰,童行偉. 鄭州白糖期貨價(jià)格的模型選擇方法[J]. 北京師范大學(xué)學(xué)報(bào)·自然科學(xué)版,2011,47(6):551~557.
[7] 周瑋. 變量選擇中的LARS算法及其在國(guó)民經(jīng)濟(jì)中的應(yīng)用[D]. 濟(jì)南:山東大學(xué),2011.
AComparativeStudyontheProcessingMethodsofMulticollinearityinDamMonitoringData
Ding Li,Qian Qiangqiang,Zhao Jun,Wu Jianye
(Huzhou Institute of Surveying and Mapping,Huzhou 313000,China)
Multicollinearity is a kind of common pathological data problem in dam safety monitoring,in order to weaken the influence on parameter estimation,principal component regression,partial least squares regression,ridge regression and lasso method are comprehensively applied to modeling analysis of dam observation data,and results are compared with multiple linear regression model’s. It shows that the multicollinearity has little effect on the model fitting and forecasting,but biased estimation methods have advantages in model interpretability and stability of model coefficients,and four kinds of biased estimation methods have their own characteristics for modeling with multicollinearity data.
multicollinearity;principal component regression;partial least squares regression;ridge regression;lasso method
1672-8262(2017)06-139-04
P207
B
2016—11—01
丁立(1989—),男,碩士,助理工程師,主要從事安全監(jiān)測(cè)數(shù)據(jù)處理相關(guān)工作。

