ABAQUS混凝土塑性損傷因子計算方法及應用研究

楊 飛， 董新勇， 周沈華， 黃余沖

(1.西安市地下鐵道有限責任公司，陜西西安 710018； 2.長安大學建筑工程學院，陜西西安 710061)

ABAQUS混凝土塑性損傷因子計算方法及應用研究

楊 飛1， 董新勇2， 周沈華1， 黃余沖2

(1.西安市地下鐵道有限責任公司，陜西西安 710018； 2.長安大學建筑工程學院，陜西西安 710061)

ABAQUS中塑性損傷模型可有效模擬混凝土在反復荷載作用下非彈性力學行為，在結構抗震性能分析中應用廣泛，但該模型中塑性損傷因子確定方法尚存在問題。文章基于GB 50010-2010《混凝土結構設計規范》中的單軸本構關系，提出并推導了計算混凝土塑性損傷模型損傷因子的實用方法，通過鋼筋混凝土簡支梁數值算例及室內試驗對三種混凝土塑性損傷因子計算方法的精度進行了對比研究。結果顯示，采用混凝土軸心強度標準值確定塑性損傷因子時，基于過鎮海單軸受力模型的能量等效法和GB 50010-2010《混凝土結構設計規范》中單軸本構關系的實用法計算簡單，且具有較好的精度，研究結論可為混凝土結構非線性抗震分析提供參考。

混凝土塑性損傷模型； 損傷因子； 計算方法； 數值分析； ABAQUS

近年來，我國西部黃土地區地鐵工程逐漸增多，黃土地區地鐵地下結構的抗震性能及安全性評價日益受到密切關注[1]。隨著地鐵地下結構抗震理論與實踐不斷進步及計算技術飛速發展，數值仿真分析可更全面、更真實再現地鐵地下車站、區間隧道等地下結構在地震荷載下的動態特性，被國內外科研工作者普遍采用。ABAQUS大型非線性有限元分析軟件，在處理黃土介質變形及土-結構動力相互作用的非線性問題時具有較好的適用性，因此在黃土地區地鐵地下結構抗震研究中應用廣泛。

ABAQUS提供了豐富的材料庫，其中混凝土塑性損傷模型為混凝土結構抗震性能研究提供了可靠途徑。該模型基于塑性損傷因子考慮材料剛度折減，能夠較準確、方便地模擬混凝土及其它脆性材料在反復荷載下的損傷退化。該軟件的用戶手冊對混凝土塑性損傷模型的基本理論及相關參數進行了詳細的介紹，但對模型中塑性損傷因子的取值未做明確規定，然而數值分析結果的準確性與塑性損傷因子的取值密切相關[2]。相關研究中混凝土塑性損傷模型的塑性損傷因子計算方法各不相同，且在確定塑性損傷因子時采用的混凝土強度代表值也不統一，張勁[3]采用圖解法原理和孟憲春[4]采用能量等效法計算混凝土塑性損傷因子時分別選取軸心強度標準值和平均值作為混凝土強度代表值。本文以西安黃土地區地鐵車站抗震研究為背景，提出并推導一種基于GB 50010-2010《混凝土結構設計規范》[5]附錄C中混凝土單軸本構關系確定塑性損傷因子的實用方法，并通過混凝土簡支梁算例及室內試驗對三種混凝土塑性損傷因子計算方法的模擬精度進行對比研究。結果顯示，采用混凝土軸心強度標準值確定塑性損傷因子時，基于過鎮海單軸受力模型的能量等效法和GB 50010-2010《混凝土結構設計規范》的實用法計算簡單，具有較好精度，研究結論可為混凝土結構非線性抗震分析提供參考。

1 ABAQUS中混凝土塑性損傷模型

ABAQUS中混凝土塑性損傷模型(以下簡稱CDP模型)是建立在Lubliner[6]和Lee and Fenves[7]模型基礎上的。該模型基于各向同性假設，采用彈性損傷結合受拉及受壓塑性替代混凝土的非彈性行為，并考慮了由于拉伸或壓縮過程中塑性應變導致的彈性剛度退化及循環荷載作用下的剛度部分恢復。

單軸往復荷載作用下，CDP模型中混凝土塑性損傷演化及剛度恢復如圖1所示。軸向受拉過程中，混凝土未到達峰值拉應力(A點)前，拉應力線性增加，峰值拉應力過后，混凝土開始出現裂縫，材料產生受拉損傷并不斷累積。受拉加載至B點卸載時，將按有效剛度(1-dt)E0產生回彈，即圖1中路徑BC。當荷載由拉力狀態轉變為壓力狀態時，拉伸裂縫在壓力作用下閉合，引起受壓剛度恢復(wc=1)，此時加載路徑為CMF。受壓加載至F點卸載時，混凝土發生了受壓塑性損傷，有效剛度退化至(1-dc)E0。當荷載由壓力狀態再次轉變為拉力狀態時，裂縫并未閉合，拉伸剛度未得到恢復，應力應變路徑沿為GH(wc=0)[8]。

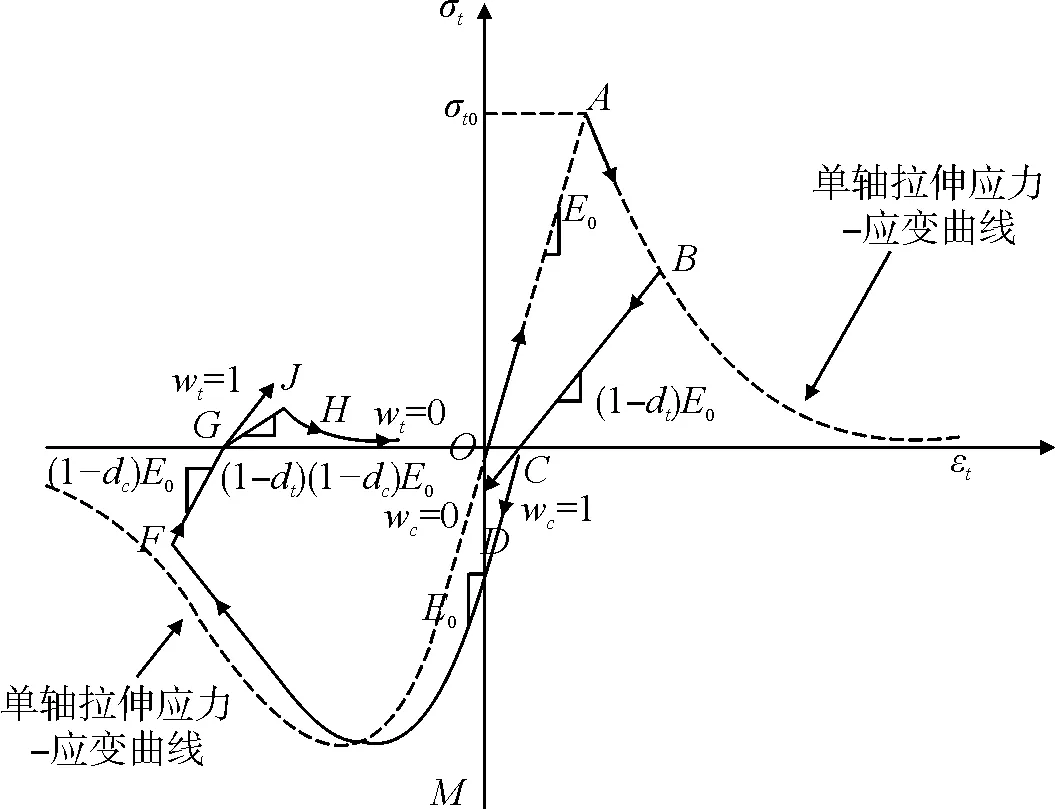
圖1 混凝土彈性模量恢復示意

ABAQUS中CDP模型是基于單軸受力狀態定義，受壓塑性變形階段材料損傷演化可用非彈性應變與受壓損傷因子關系曲線定義，受拉開裂階段材料損傷發展可用開裂應變與受拉損傷因子關系曲線定義。

2 塑性損傷因子的計算方法

2.1 基于過鎮海單軸受力曲線的能量等效法

能量等效原理由Sidoroff于1981年提出，即應力作用在無損材料與作用在受損材料所產生的彈性余能在形式上相同[9-10]，只要將Cauchy應力改為等效應力，并考慮剛度折減將初始彈性模量取為等效受損彈性模量。根據能量等效假設，材料的應力應變關系可表示為：

σ=E0(1-d)2ε

(1)

基于過鎮海單軸受力曲線[11]和能量等效假設，可得混凝土受壓塑性損傷因子見式(2)、式(3)：

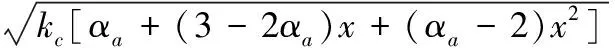
(2)

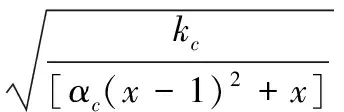
(3)

混凝土受拉損傷因子見式(4)：

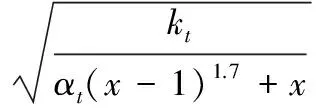
(4)

2.2 基于過鎮海單軸受力曲線的圖解法

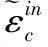
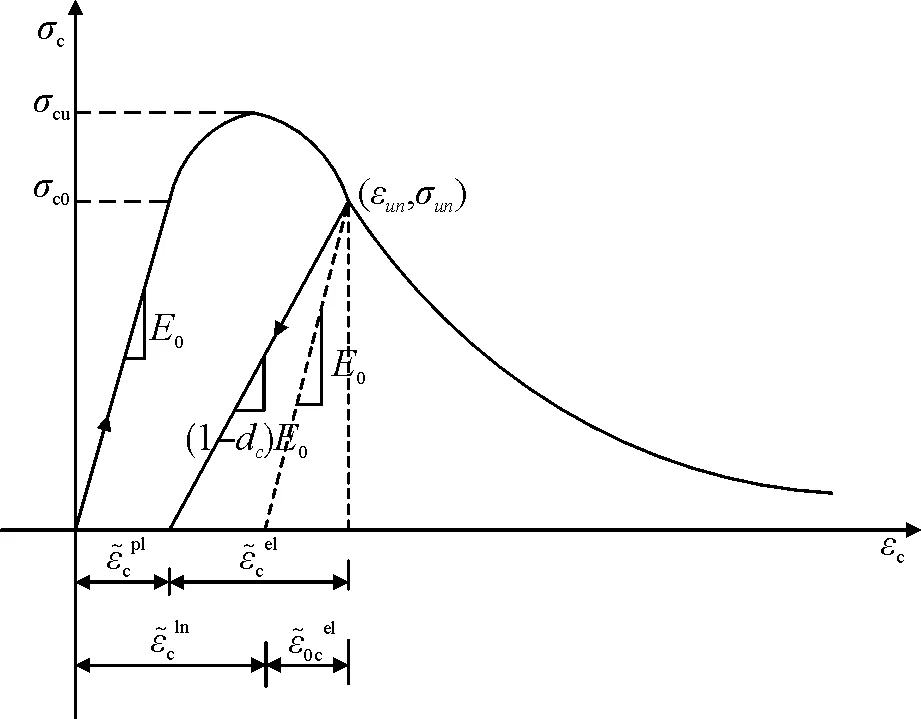
圖2 混凝土單軸受壓損傷演化

圖3 混凝土單軸受拉損傷演化

由圖中的幾何關系可得受壓和受拉塑性損傷因子見式(5)：

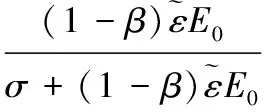
(5)

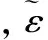
2.3 基于GB 50010-2010規范的實用法

我國現行GB 50010-2010《混凝土結構設計規范》(以下簡稱“10混規”)中混凝土單軸應力應變曲線如圖4所示[5]。單軸受壓曲線方程如式(6)：

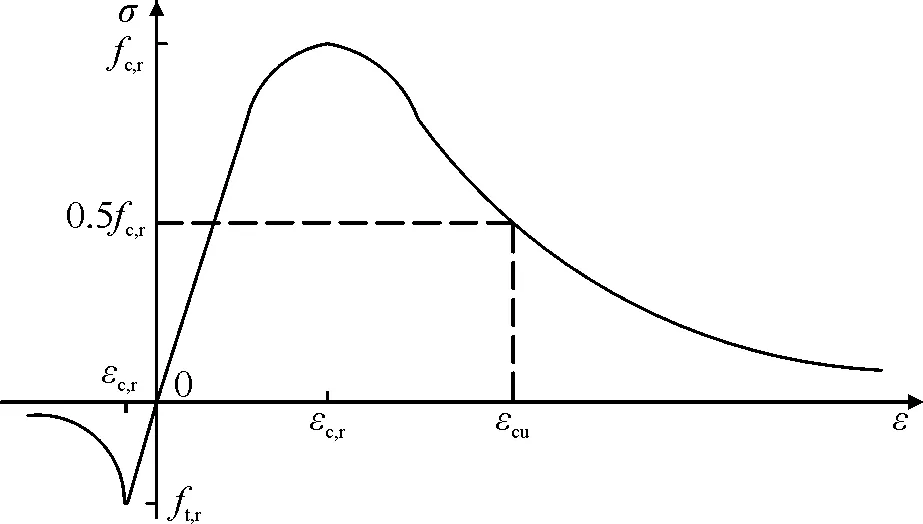
圖4 GB 50010-2010中混凝土單軸本構曲線

(6)

單軸受拉曲線方程如式(7)：

σt=Ec(1-Dt)εt

(7)

其中D取值可按“10混規”中的方法計算，式中用參數D表示混凝土損傷演化參數，以區別于ABAQUS中CDP模型的塑性損傷因子d。為將“10混規”中的損傷演化參數用于ABAQUS中CDP模型，需建立“10混規”中損傷演化參數與CDP模型塑性損傷因子之間的關系。

Lemaitre在1971年從細觀尺度分析，并提出描述材料損傷的應變等效原理，可反映出材料的損傷演化過程[14]。該原理假設材料在有效應力下產生損傷后，其應變與無損傷應變等效。根據應變等效原理，可由無損傷材料的本構關系導出損傷材料的本構關系，其中應力要用等效應力代替。根據應變等效假設可得式(8)：

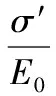
(8)

從而，材料的應力應變關系可表示為式(9)：

σ=E0(1-D)ε

(9)

從式(9)中分析發現，基于應變等效假設的材料損傷演化過程中無塑性應變，是一種彈性損傷模型(圖5)。由式(6)、式(7)與式(9)的對比分析可知，“10混規”提出的單軸受力本構模型中的損傷演化參數D是基于應變等效假設的彈性損傷參數，不同于CDP模型中的塑性損傷因子d(圖5)。

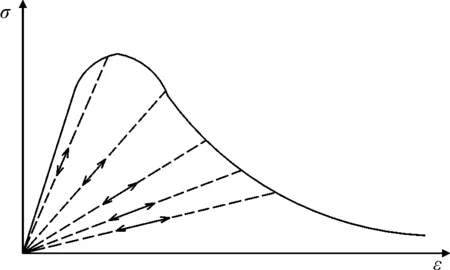
(a) 彈性

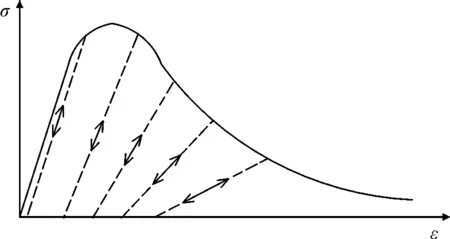
(b) 塑性圖5 彈、塑性損傷模型示意

對比分析能量等效假設與應變等效假設，發現有如下關系見式(10)：

E0(1-D)=E0(1-d)2

(10)

從而推出式(11)：

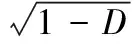
(11)

因此，“10混規”提出的單軸受力本構模型中的損傷演化參數D不能直接用于CDP模型，將其按式(11)轉換為塑性損傷因子之后，可用于ABABQUS中CDP模型。

3 三種混凝土塑性損傷因子算法的對比分析

上述三種塑性損傷因子的計算均需確定混凝土單軸強度代表值，可結合“10混規”取軸心強度標準值或平均值。為了對比分析不同計算方法及不同單軸強度代表值確定混凝土塑性損傷因子的可靠度，本文采用不同方法確定混凝土塑性損傷因子，基于ABAQUS的CDP模型，對鋼筋混凝土簡支梁受力變形過程進行了數值分析，并通過室內承載力試驗驗證數值分析結果，研究不同塑性損傷因子確定方法的精度。

3.1 CDP模型中塑性損傷因子的計算

以C30混凝土為例，采用“10混規”中的軸心強度標準值和平均值分別計算CDP模型塑性損傷因子。C30混凝土軸心抗壓強度標準值為20.1 MPa，軸心抗拉強度標準值取為2.01 MPa；軸心抗壓強度平均值為28.0 MPa，軸心抗拉強度平均值取為2.80 MPa；混凝土泊松比取0.2。

為方便表述，本文將能量等效法、圖解法及基于“10混規”實用法的計算結果分別用A、B和C表示，用角標1和角標2分別表示采用混凝土軸心強度標準值和軸心強度平均值的計算值。混凝土塑性損傷因子計算結果如圖6、圖7所示。

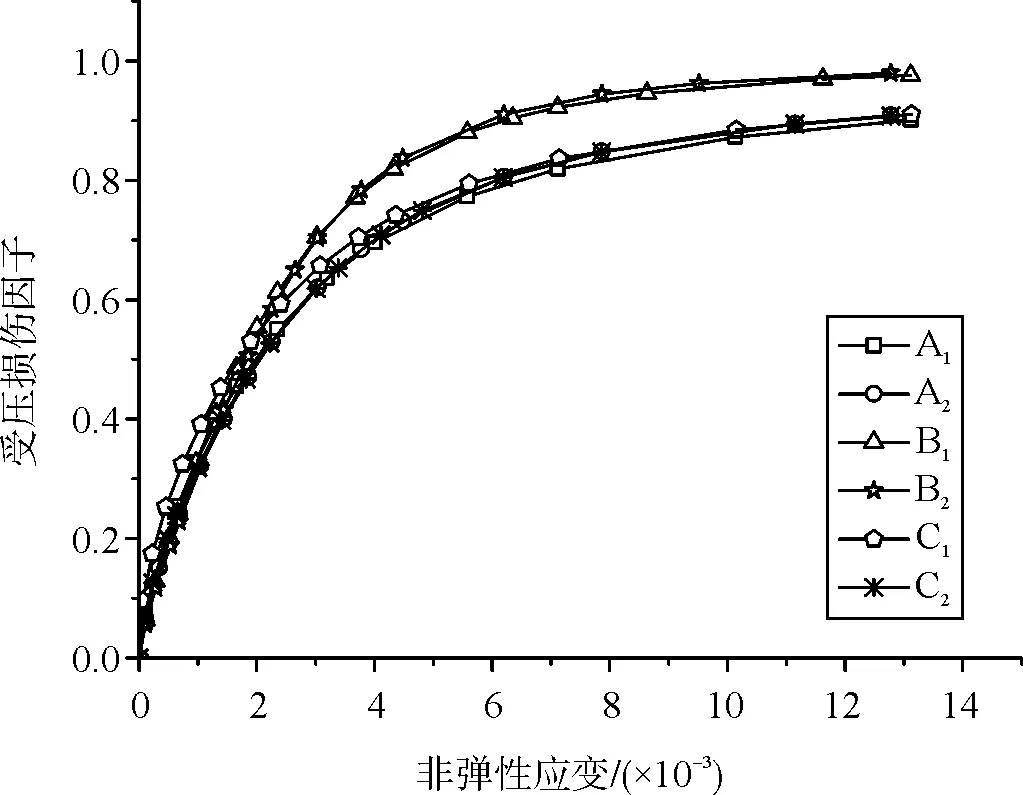
圖6 非彈性應變-受壓損傷因子關系曲線

圖7 開裂應變-受拉損傷因子關系曲線

3.2 數值分析及試驗模型

在ABAQUS中建立鋼筋混凝土簡支梁模型，截面及配筋如圖8所示。為了防止混凝土簡支梁局部受壓破壞，在支座和加載點設置厚度為6 mm的鋼墊板。簡支梁所用混凝土為C30，采用ABAQUS中的CDP本構模型，使用三維8節點縮減積分實體單元C3D8R模擬；縱向鋼筋及箍筋強度標準值為300 MPa，采用Plasticity本構模型，使用三維2節點桁架單元T3D2模擬；采用Interaction模塊中Embedded將鋼筋骨架嵌入混凝土中，模擬兩者之間的約束變形機理；鋼筋混凝土簡支梁室內試驗模型尺寸及配筋同數值分析模型。

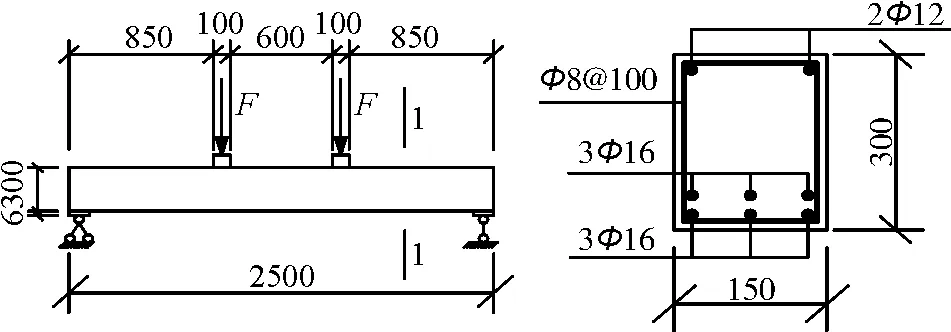
圖8 鋼筋混凝土梁及配筋示意

3.3 結果分析

采用不同方法確定CDP模型的塑性損傷因子，分別計算鋼筋混凝土簡支梁荷載-撓度曲線(圖9～圖10)。當采用混凝土軸心強度標準值確定CDP模型塑性損傷因子時，鋼筋混凝土梁的荷載-撓度曲線呈現出明顯的屈服平臺，發生了較大的塑性變形，即梁破壞形態屬于適筋梁延性破壞。當采用混凝土軸心強度平均值確定CDP模型塑性損傷因子時，鋼筋混凝土梁的荷載-撓度曲線呈現出明顯陡直跌落特征，即梁發生脆性破壞。

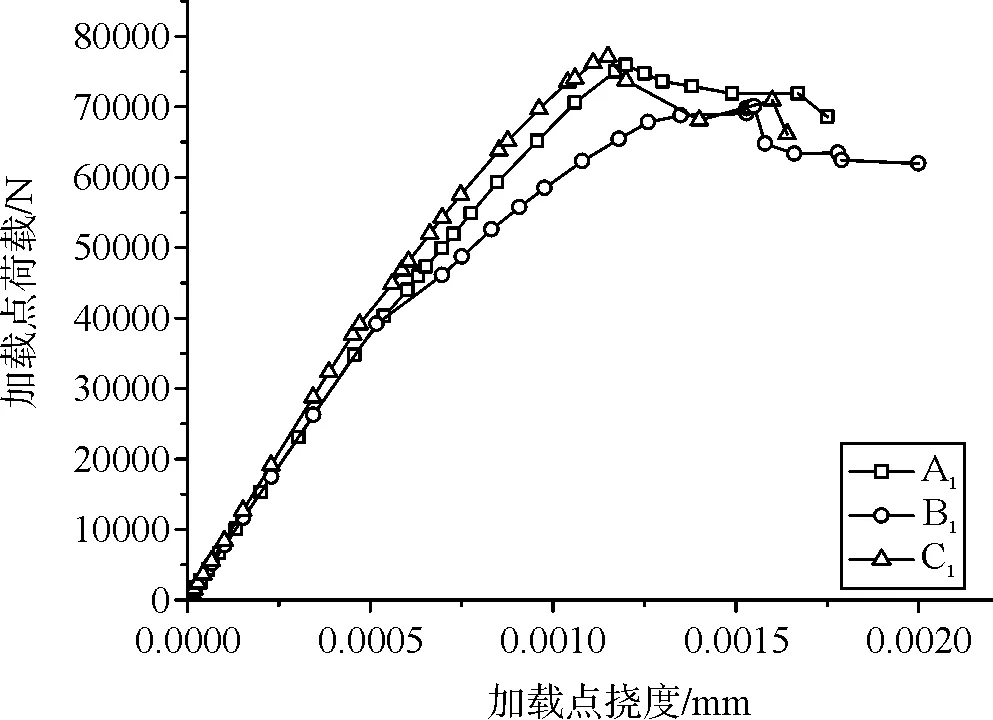
圖9 基于軸心強度標準值的分析結果

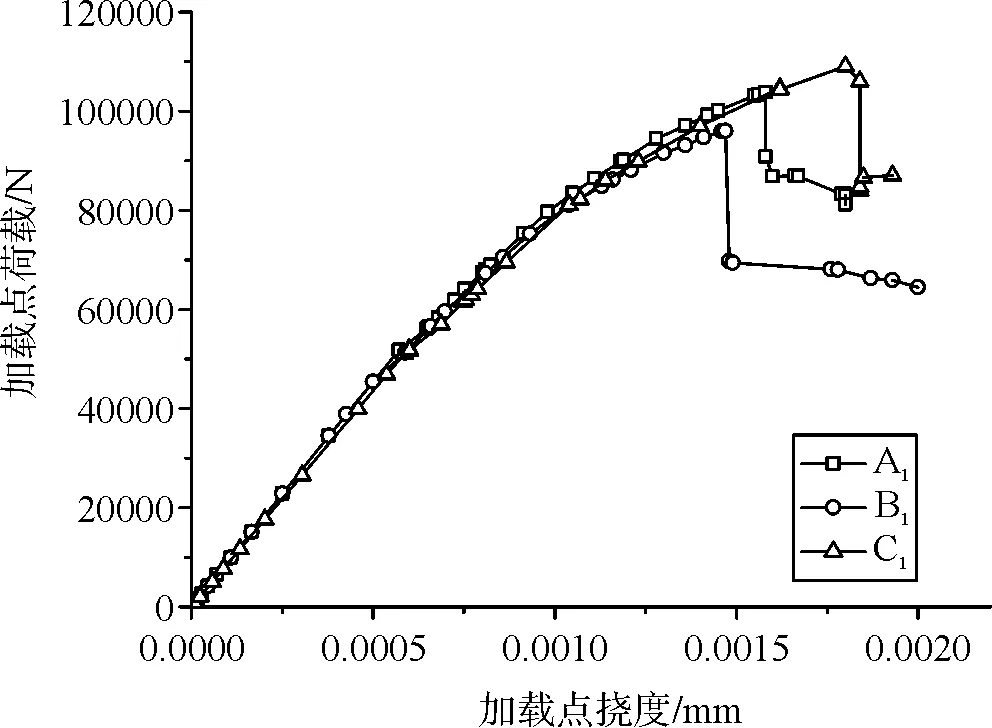
圖10 基于軸心強度平均值的分析結果

為了驗證數值分析結果，按數值模型中的尺寸、材料及配筋澆筑鋼筋混凝土簡支梁試件，并進行了室內承載力試驗，其破壞形態為延性破壞。基于軸心強度標準值確定CDP模型的塑性損傷因子，數值分析結果可反應鋼筋混凝土梁的實際受力水平，其破壞形態與試驗結果相符；而基于軸心強度平均值確定塑性損傷因子，數值分析中混凝土的強度高于實際值，從而使分析結果呈現出少筋梁的脆性破壞形態。因此，可推斷在ABAQUS中應用CDP模型時，基于混凝土軸心強度標準值確定塑性損傷因子，具有較好的可靠性。

由鋼筋混凝土簡支梁的破壞荷載，可計算出該梁所承受的極限彎矩。將數值分析得出的計算極限彎矩與室內試驗獲得的極限彎矩進行對比分析，可得不同方法確定塑性損傷因子時，數值分析結果相對于室內試驗結果的誤差，對比分析結果見表1。基于軸心強度標準值確定混凝土塑性損傷因子時，數值分析計算極限彎矩與室內試驗中極限彎矩較接近，相對誤差為0.97 %～6.7 %；而基于軸心強度平均值確定混凝土塑性損傷因子時，數值分析結果與試驗值有較大差距，極限彎矩相對誤差為20.6 %～37 %，進一步驗證了基于混凝土軸心強度標準值確定塑性損傷因子，具有較好的可靠性。從鋼筋混凝土梁極限彎矩分析結果可知，基于軸心強度標準值確定混凝土塑性損傷因子，采用基于過鎮海單軸受力曲線的等效能量法和基于“10混規”的實用法時，數值分析計算極限彎矩與室內試驗中極限彎矩的相對誤差分別為0.97 %和2.6 %，均具有較高的精度。

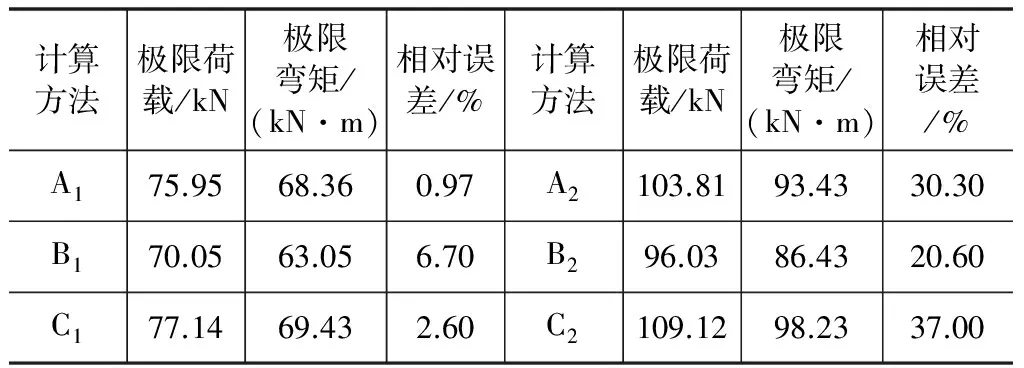
表1 不同混凝土塑性損傷因子計算方法的分析結果

4 結論

本文提出了基于“10混規”計算ABAQUS中CDP模型塑性損傷因子的實用方法，并通過鋼筋混凝土簡支梁數值算例和室內試驗對能量等效法、圖解法和基于“10混規”的實用法計算CDP模型塑性損傷因子的可靠性進行了對比研究，可為混凝土結構非線性抗震分析提供參考，得出以下結論：

(1)對比分析表明，基于軸心強度標準值確定CDP模型塑性損傷因子時，數值模擬的破壞形態與室內試驗相同，且數值計算的極限彎矩與試驗值相對誤差較小，為0.97 %～6.7 %；基于軸心強度平均值確定CDP模型塑性損傷因子時，數值計算極限彎矩與試驗值相差較大，為20.6 %～37 %，且數值模擬破壞形態與實際破壞形態不同。因此，基于混凝土軸心強度標準值確定CDP模型塑性損傷因子，具有較好的可靠性。

(2)確定混凝土塑性損傷因子時，發現“10混規”中單軸受力模型提供的損傷演化參數D描述的損傷過程中不發生塑性變形，屬于彈性損傷模型，由此推導了將其轉化為塑性損傷因子的計算公式，提出了基于“10混規”計算ABAQUS中CDP模型塑性損傷因子的實用方法。同時，數值模擬與室內試驗結果的對比分析表明，基于“10混規”的實用法確定CDP模型塑性損傷因子具有較高的模擬精度。

(3)基于“10混規”的實用法與能量等效法、圖解法相比，在ABAQUS數值建模與計算中具有計算方便、收斂較快的優點。

(4)本文對比了三種塑性損傷因子計算方法的數值模擬結果，對ABAQUS中CDP模型塑性損傷因子的取值提出有益的建議，有利于在混凝土材料非線性抗震分析中得到可靠的結果。

[1] 權登州, 王毅紅, 井彥林, 等.黃土地區地鐵車站數值模型及測試位置研究[J].震災防御技術, 2015, 10(1): 108-115.

[2] 秦浩,趙憲忠.ABAQUS混凝土損傷因子取值方法研究[J].結構工程師,2013,29(6):27-32.

[3] 張勁,王慶揚,胡守營, 等.ABAQUS混凝土損傷塑性模型參數驗證[J].建筑結構,2008,38(8):127-130.

[4] 孟憲春,景立平.多層地鐵車站振動臺試驗與數值分析[D].哈爾濱：中國地震局工程力學研究所，2011: 31-46.

[5] GB 50010-2010 混凝土結構設計規范[S].

[6] LUBLINER J, OLIVER J, OLLER S, et al. A plastic-damage model for concrete [J]. International Journal of Solids and Structures, 1989, 25(3): 299-326.

[7] LEE J, FENVES G. Plastic-damage model for cyclic loading of concrete structures [J]. Journal of Engineering Mechaniccs, 1988, 124(8): 892-900.

[8] ABAQUS Inc. Abaqus analysis user.’s manual [M]. 2010.

[9] KRAJCINOVIC D, FONSEKA G. The continuous damage theory of brittle materials, Part 1: General Theory [J]. Journaal of Applied Mechanics, 1981, 48(4): 809-815.

[10] 曹明.ABAQUS損傷塑性模型損傷因子計算方法研究[J].道路工程，2012(2) : 51-54.

[11] GB 50010-2002 混凝土結構設計規范[S].

[12] 陸新征,葉列平,繆志偉, 等.建筑抗震彈塑性分析[M].北京：中國建筑工業出版社，2009: 121-125.

[13] 張勁,王慶揚,胡守營, 等. ABAQUS混凝土損傷塑性模型參數驗證[J].建筑結構,2008,38(8)：127-130.

[14] 李兆霞.損傷力學及其應用[M].北京：科學出版社，2002: 16-19.

[定稿日期]2017-07-28

國家自然科學基金資助項目(編號：41472267)；西安市地下鐵道有限責任公司科研基金項目(編號：D4-YJ-042014048)

楊飛(1983～)，男，本科，工程師，主要從事地下結構抗震設計方面工作;董新勇(1990～)，男，碩士研究生，主要從事建筑結構抗震、混凝土結構以及生土結構方面研究；周沈華(1980～), 男，碩士，高級工程師，主要從事巖土與地下工程抗震研究。

TU311.4

A