自動化碼頭起重機和自帶提升功能的AGV的集成調度

添玉 +王建彬 +范會方

摘要：為深入研究新工藝帶來的自動化碼頭設備集成調度問題，針對自動化碼頭的一種自帶提升功能的自動導引小車（LAGV）和緩沖支架系統，提出新的設備集成調度框架。考慮不同設備之間的相互關聯和制約的協同關系，將岸橋分配調度與LAGV、場橋調度分開，合理定義兩種任務（兩個問題）的劃分方式，建立兩個多目標混合整數規劃模型。設計一種具有內外層關聯的適應度函數的雙層遺傳算法。相對傳統聯合調度算法，該算法平衡了計算復雜性與調度均衡性。最后的數值試驗證明了模型和算法的有效性。從岸橋數量、任務規模、AGV數量和調度策略等對岸橋等待時間的影響上，對采用LAGV的系統和采用傳統AGV的系統進行比較，為自動化碼頭裝卸作業調度提供決策支持。

關鍵詞：

自動化碼頭； 自動導引小車（AGV）； 集成調度； 遺傳算法（GA）； 啟發式策略

中圖分類號： U691.3

文獻標志碼： A

Integrated scheduling of cranes and AGVs with lifting function in automated container terminals

TIAN Yu1， WANG Jianbin1， FANG Huifang2

（1. Logistics Engineering College， Shanghai Maritime University， Shanghai 201306， China；

2. Software Automation Department， ZPMC Electric， Shanghai 200125， China）

Abstract：

In order to further study the issue of integrated equipment scheduling caused by new techniques in automated terminals for automated guided vehicles with lifting platforms （called LAGV） and buffer support system in automated terminal， a new integrated scheduling framework is proposed. Considering the interrelated and constrained cooperativeness relations among different equipments， it is divided into two problems， the quay crane allocation/scheduling problem and the LAGV and yard crane scheduling problem. By reasonably defining the division of two tasks （two problems）， two multiobjective mixedinteger programming models are established sequentially. A twolayer genetic algorithm is developed， where a fitness function is proposed to interlink two layers. The algorithm leads to the tradeoff between the computational complexity and the scheduling equilibrium compared with traditional joint scheduling algorithms. A numerical test is carried out in order to evaluate the performance of the model and algorithm. The system adopting LAGVs is compared with the system adopting traditional AGVs through investigating the influence of the number of quay cranes， the scale of tasks and the number & scheduling strategies of AGVs on the waiting time of quay cranes. The results provide decision support for automated terminal handling operations.

Key words：

automated terminal； Automated Guided Vehicle （AGV）； integrated scheduling； Genetic Algorithm （GA）； heuristic strategy

0引言

在新的全球經濟格局下，如何提高集裝箱碼頭運作效率成為當前碼頭發展亟待解決的問題。而在碼頭實際作業過程中，碼頭整體作業效率的提升依賴于岸橋、水平運輸車輛、場橋等主要設備的密切協作與合理調度。因此，碼頭設備調度問題成為當前研究的熱點。

目前，國內外專家對集裝箱碼頭優化調度問題已經做了大量的研究。文獻[13]僅研究碼頭單個環節調度，通過模型構建、算法設計及案例分析研究碼頭設備調度問題，但未考慮碼頭多個環節之間的相互影響。文獻[49]在研究集裝箱碼頭設備調度問題時，考慮了多環節作業之間的相互作用和制約，建立了多類型設備集成調度模型。碼頭新工藝的出現對調度問題產生了很大影響，文獻[1012]針對碼頭新工藝下的設備調度問題，采用構建模型、仿真模型及實驗分析等方法進行研究。endprint

當前的研究主要針對碼頭一種或兩種設備的聯合調度，且大多數集中在傳統碼頭領域，缺乏將不同新工藝用于碼頭設備集成調度的深入研究。本文建立岸橋（QC）、自帶提升功能的自動導引小車（LAGV）和支架、自動化場橋（AYC）集成調度混合整數規劃模型，并設計雙層遺傳算法對問題進行求解。

1問題描述

圖1展示了自動化碼頭的一種新工藝布局，其裝卸運輸系統由4部分組成：QC，LAGV，緩沖支架以及AYC。QC負責船舶裝卸，LAGV負責水平運輸，AYC負責場區的存/取操作。作為連接水平運輸和堆場操作的柔性機制，緩沖支架減少水平運輸設備和自動化軌道吊相互等待時間，緩解水平運輸能力與自動化軌道吊裝卸堆放能力之間的矛盾，提高系統作業效率，但也增加了設備調度復雜性。

考慮任務執行過程中各裝卸環節的銜接以及各裝卸設備之間存在時空非同步性影響，分析碼頭裝卸作業調度系統，可知各子環節調度存在目標沖突、

裝卸資源請求沖突、響應結果沖突。因此，QC調度問題、水平運輸調度問題、AYC調度問題相互影響、緊密關聯，必須在有效解決上述沖突的情況下合理協調各種調度決策才能達到最優的整體運作效果。

2集成調度模型

2.1調度框架

對于集裝箱裝卸任務的劃分，BIERWIRTH等[13]將其分為5種：①基于貝位區域；②基于單個貝位；③基于堆垛的任務；④基于集裝箱簇；⑤基于單個集裝箱。

定義兩層調度子問題的不同任務劃分方式：上層采用集裝箱簇作為任務定義，既避免由于基于單個集裝箱任務定義導致的QC各種十分復雜的干擾約束的出現，和任務量的龐大造成求解時間和空間復雜度指數性增加，又不會因任務定義太大而導致QC作業難以均衡；下層是AGV和場橋的調度，采用基于單個集裝箱的任務定義，有利于AGV運輸的靈活性和場橋重進重出的高效率，也便于與上層進行任務單位的銜接。

如圖2所示，設備集成調度框架是在已知船舶配載計劃、QC屬性、任務屬性的情況下，通過基于簇任務的QC分配與調度模型求解各QC的箱任務序列，為基于箱任務序列的自動化設備集成調度模型提供一定的輸入條件，而將后者求解出的箱任務結束時刻反饋給前者，作為QC調度的評估，不斷重復該邏輯，最后得到各設備的最優任務序列。

2.2基于簇任務的QC分配與調度模型

2.2.1假設條件

（1）計劃期內船舶泊位計劃已知，船舶上貝位連續分布，且每個貝位在岸線方向上的長度相同；

（2）每個集裝箱簇任務所在貝位、作業類型、最短理想作業時間、先后作業順序、簇內集裝箱的作業順序均已知；

（3）單船設有同時作業最多和最少QC數；

（4）所有QC在同一軌道上水平勻速移動且不能跨越作業，相鄰QC之間滿足安全距離要求。

2.2.2符號說明

K為QC的集合，K={1，2，…，k，…，C}；T為計劃期內時間段的集合，T={1，2，…，t，…，P}；Ω為所有簇任務集合，Ω={1，2，…，n，…，N}，用m表示同臺QC上任務n的前任務；ψ為不能同時作業的簇任務集合；Φ為有作業先后順序要求的簇任務集合；Rmin和Rmax分別表示為船舶分配的最少和最多QC數；Ta為船舶到達時刻；Tb為船舶靠泊時刻；Tn為簇任務n的理想最短作業時間；ln為簇任務n的位置，用貝位編號表示；Δl為相鄰QC的安全距離，用間隔貝位數表示，通常為一個貝位；vk為第k臺QC的水平移動速度，m/min，k∈K；M為一個充分大的正整數；Ts和Te分別表示船舶開始作業和結束作業時刻；Tsn，Ten分別為簇任務n的真實開始時刻和結束時刻，Tsn為簇任務n的允許作業時刻；ckn為第k臺QC服務簇任務n后的空閑時刻，每次任務完成后立即更新；lkn為第k臺QC完成簇任務n時位于碼頭岸線上的位置，每次任務完成后立即更新；δkn為第k臺QC為完成簇任務n移動到合適位置所需的時間；xtk為01變量，若第t時段有第k臺QC為船舶進行裝卸作業，則為1，否則為0；ztkn為01變量，若第t時段有第k臺QC為簇任務n作業，則為1，否則為0；fn1n2為01變量，若簇任務n2開始作業時，簇任務n1已經完成，則為1，否則為0，n1，n2∈Ω。

2.2.3目標函數

（1）最小化船舶在港時間

S1=min（Te-Ta）=min（（Te-Ts）+（Ts-Ta））

其中：Te-Ts表示船舶的裝卸作業時間；Ts-Ta表示船舶的等待作業時間，包含等待泊位時間和等待岸橋時間。

（2）最小化QC移動距離

S2=min knztkn·vk·δkn=

min knT（ztkn（|lkn-lkn′|+

k′|ln-（k-k′）Δl-l′k′n′|））

當進行裝卸作業時，QC的狀態是不斷變化的，當第k臺QC對船舶上的簇任務n進行作業時，其位置和再次空閑時刻需要更新：

lkn=ztknln

ckn=ztknTen

由于QC不能跨越作業，某QC k′可能會因為其他作業需要而被迫移動，其位置和空閑時間更新如下：

l′kn=ztkn（ln-（k-k′）Δl）

c′kn=ztkn（c′kn′+ln-（k-k′）Δl-l′k′n′/vk）

2.2.4約束條件

Ts≥Tb （1）

Te≥max（Ten），n∈Ω （2）

Rmin≤kxtk≤Rmax，t∈T （3）

nztkn=xtk，t∈T；k∈K；n∈Ω （4）

tkztkn≥Tn，n∈Ω （5）

zt1k1n+zt2k2n=1，t1，t2∈{Tsn，…，Ten}；endprint

k1，k2∈K，k1≠k2； n∈Ω （6）

Tsn≥max{（ckm+δkn）ztkn，Tsn}，

t∈T；k∈K；m，n∈Ω （7）

Ten≥Tsn+Tn，n∈Ω （8）

fn1n2+fn2n1=1，（n1，n2）∈ψ （9）

Ten1-Tsn2≤0，（n1，n2）∈Φ （10）

Ten1≤Tsn2+M（1-zt1kn1zt2kn2fn1n2），

t1，t2∈T； k∈K； n1，n2∈Ω （11）

（lk2n2-lk1n1）（ln2-ln1）ztk1n1ztk2n2≥0 （12）

xt，k-1+xt，k+1-xt，k={-1，0，1}，

t∈T； k-1，k，k+1∈K （13）

式（1）表示船舶的開始作業時刻必須大于其靠泊時刻。式（2）表示所有簇任務作業完成時間即為船舶結束作業的時間。式（3）表示每個時刻為船舶服務的船舶數量在一定范圍內。式（4）表示在單位時間內一臺QC只能為一個任務服務。式（5）表示每個簇任務都配置了相應的QC作業，并且QC作業時間應滿足簇任務所需的裝卸作業時間要求。式（6）表示有且僅有一臺QC為簇任務n服務。式（7）表示簇任務n的開始作業時刻。式（8）表示簇任務n的作業結束時刻。式（9）表示對不能同時作業的簇任務的限定。式（10）表示有先后順序的簇任務在時間上的關系。式（11）表示兩個簇任務由同一臺QC服務時，其作業時間需要滿足的關系。式（12）表示QC不能在同一船舶的兩個作業之間交叉作業。式（13）表示任意時間若有多臺QC為該船舶服務，則QC必須連續，即滿足QC不能跨越原則。

2.3基于箱任務序列的自動化設備集成調度模型

2.3.1假設條件

（1）集港在裝卸船作業過程之前已經完成，疏港在裝卸船作業過程之后進行。

（2）通過QC調度模型得到每臺QC所負責的簇任務和箱任務序列。

（3）調度計劃期內，已知每個箱任務操作類型（裝/卸），在船上和堆場的裝卸位置。

（4）QC，LAGV和AYC的可用數量已知，且每個設備一次只處理一個集裝箱。

（5）LAGV，AYC空/重載和QC的速度以及各個設備的裝卸效率。

（6）每個堆場箱區僅岸側AYC負責裝卸船；不考慮LAGV堵塞情況；已知LAGV和AYC在任何兩個操作節點位置之間的距離。

2.3.2符號變量說明

ve和vd分別表示提供AYC初始和結束虛擬任務的虛擬岸橋。vs和vf分別表示提供LAGV初始和結束虛擬任務的虛擬岸橋。Q為AYC的集合。V為LAGV的集合。P為堆場岸側交換區的集合。mk為第k臺QC執行的任務數量，k∈K。eki為QC在作業區開始作業箱任務（k，i）事件，當箱任務（k，i）為卸船任務時，表示QC開始放箱到LAGV；當箱任務（k，i）為裝船任務時，表示QC開始從LAGV上抓箱；（k，i）為箱任務編號，代表第k臺QC的第i個箱任務，k∈K，i=1，…，mk。Eaki為LAGV在堆場岸側交換區開始作業箱任務（k，i）事件，當箱任務（k，i）為卸船任務時，表示LAGV開始將其頂升到支架；當箱任務（k，i）為裝船任務時，表示LAGV開始從支架處接箱，k∈K。Ebki為AYC在堆場岸側交換區開始作業箱任務（k，i）事件，當箱任務（k，i）為卸船任務時，表示AYC開始從支架上抓箱；當箱任務（k，i）為裝船任務時，表示AYC開始放箱到支架，k∈K。TL為裝船任務的事件eki的集合，k∈K，即eki∈TL。TD為卸船任務的事件eki的集合，k∈K，即eki∈TD。TC為事件eki集合中有先后順序要求的任務集合，k∈K，即eki∈TC。Nq為第q臺AYC執行Ebki的集合，k∈K，q∈Q。Np為第p個堆場岸側交換區事件Eaki的集合，k∈K，p∈P。ski為第k臺QC執行事件eki的實際準備就緒時刻，k∈K。Hkik（i-1）為第k臺QC完成ek（i-1）后執行eki的全部準備時間，k∈K，i≠1。yki為事件eki的實際發生時刻，k∈K。Yaki為事件Eaki的發生時刻，k∈K。Ybki為事件Ebki的發生時刻，k∈K。Tljki為從Ebki發生的位置到Eblj發生的位置之間AYC的純移動時間，k∈{ve}∪K，l∈{vd}∪K，j=1，…，ml，mve=mvd=|Q|。Gljki表示AYC完成Ebki后執行Eblj需要調整的時間，k∈{ve}∪K，l∈{vd}∪K。 tljki為從eki發生的位置到elj發生的位置LAGV的純運行時間，k∈{vs}∪K，l∈{vf}∪K，mvs=mvf=|V|。cljki為LAGV完成eki后去完成elj的調整時間，k∈{vs}∪K，l∈{vf}∪K。Sljki為eki與Ealj兩個事件間的調整時間，k∈{vs}∪K，l∈{vf}∪K。Ski為eki與Eaki兩個事件間的調整時間，k∈K。ΔSki為Eaki與Ebki兩個事件間的間隔時間，k∈K。ljki為01變量，若同一輛LAGV完成eki后緊接著完成elj，則其值為1，否則為0，k∈{vs}∪K，l∈{vf}∪K。φljki為01變量，若同一臺AYC完成Ebki后緊接著完成Eblj，則其值為1，否則為0，k∈{ve}∪K，l∈{vd}∪K。

2.3.3目標函數及約束

i=1，…，mk；j=1，…，ml

S3=min k∈Kmki=1（yki-ski）+ （14）

S4=min k∈{ve}∪Kmki=1l∈K∪{vd}mlj=1Tljkiφljki （15）

S5=min k∈{vs}∪Kmki=1l∈K∪{vf}mlj=1tljkiljki （16）endprint

l∈{vf}∪Kmlj=1ljki=1，k∈{vs}∪K

（17）

k∈{vs}∪Kmki=1ljki=1，l∈{vf}∪K

（18）

l∈{vd}∪Kmlj=1φljki=1，k∈{ve}∪K

（19）

k∈{ve}∪Kmki=1φljki=1，l∈{vd}∪K

（20）

ylj-max（yki+cljki，slj）≥M（ljki-1），

k∈{vs}∪K；l∈K

（21）

Yblj-（Ybki+Gljki）≥M（φljki-1），

k∈{ve}∪K；l∈K

Yalj-（yki+Sljki）≥M（ljki-1），

（22）

k∈{vs}∪K；l∈K （23）

yki-yk（i-1）≥ski-sk（i-1），k∈K；i≠1 （24）

yki≥ski，k∈K （25）

ski≥yk（i-1）+Hkik（i-1），k∈K；i≠1 （26）

yki≥Yaki+Ski，eki∈TL；k∈K （27）

Yaki≥Ybki+ΔSki，eki∈TL；k∈K （28）

Yaki≥yki+Ski，eki∈TD；k∈K （29）

Ybki≥Yaki+ΔSki，eki∈TD；k∈K （30）

Ybki-Ybkj≥0，

Ebki，Ebkj∈Nq；k∈K；

i>j；q∈Q （31）

Ybki-Yblj≥0，Ebki，Eblj∈Nq；k，l∈K；

eki，elj∈TC；yki>ylj；q∈Q （32）

式（14）～（16）為目標函數，分別表示最小化QC延遲時間、最小化AYC總移動時間、最小化LAGV的總運行時間。式（17）～（20）表示LAGV或AYC一次只能執行一個任務，一個任務一旦由某個AYC或LAGV執行就不能中斷，且每個任務都要被執行。式（21）和（22）表示由同一裝卸運輸設備執行的相鄰任務的時間邏輯關系，式（21）表示同一輛LAGV完成eki后去執行elj需要有時間cljki準備及岸橋時間準備，式（22）表示同一臺AYC完成Ebki后去執行Eblj需要有時間tljki準備。式（23）表示作業不同環節的時間邏輯關系，如果任務（k，i）和（l，j）是同一輛LAGV的兩個相鄰任務，那么LAGV完成eki后需要時間Sljki調整去完成Eblj。式（24）表示同一臺QC執行相鄰任務的調整時間應滿足QC執行所需作業的時間。式（25）表示eki的實際發生時刻最小為最早可能發生時刻。式（26）表示QC執行ek（i-1）后需時間Hkik（i-1）準備才能執行任務eki。式（27）和（28）表示對于同一裝船任務（k，i），作業相鄰環節的時間邏輯關系，此類任務的設備操作順序是：AYC→LAGV→QC，因此AYC完成Ebki時刻與Eaki和Ebki的調整時間之和不會超過LAGV完成Eaki的時刻，LAGV完成Eaki的時刻與Eaki和eki的調整時間之和不會超過QC完成eki的時刻。同理，式（29）和（30）表示對于同一卸船任務（k，i），其作業相鄰環節的時間邏輯關系。此類任務的設備操作順序是：QC→LAGV→AYC。式（31）表示每臺AYC的任務執行順序需要符合QC任務序列中的順序。式（32） 表示每臺AYC執行具有約束關系的任務必須符合它們的先后順序。

3雙層多目標遺傳算法設計

上述模型中的調度子問題均為NP難問題，本文設計雙層多目標遺傳算法求解：外層優化QC簇任務作業序列；內層基于外層的QC箱任務序列優化LAGV和AYC的任務序列，然后計算相關的評價指標值并將其反饋到外層，作為外層染色體的評價準則；通過內外層遺傳算法的協調確定最優的集成調度方案。其算法流程見圖3。

3.1染色體編碼

主要考慮兩個位串編碼，外層位串表示QC分配調度的簇任務序列， 內層位串表示LAGV和AYC調度中的箱任務序列；內外層均采用自然數對染色體編碼，每個染色體代表所有任務的一個隨機排列，每個自然數代表任務編號，染色體長度等于任務數量。

3.2不可行和重復序列的修正策略

隨機生成或迭代更新的染色體可能存在不可行或重復個體的情況，因此需進行修正。

針對不可行序列的修正策略：外層簇任務序列根據不同時、有先后關系的簇任務約束進行染色體的修正；而內層遺傳算法是在外層遺傳算法獲得的可行QC的作業序列的基礎上進行的，因此內層箱任務序列需要與外層所得的QC作業箱任務序列一致。

步驟1按外層算法所得的每個QC作業箱任務序列修正隨機產生的箱任務序列，得到符合每個QC作業序列的箱任務序列。

步驟2按簇任務約束關系來修正箱任務順序。根據QC調度序列，不同時、有先后關系的簇任務若由同一臺QC完成，那么已經在步驟1中修正。若它們不由同一臺QC完成，則應修正編碼使其滿足約束關系。采取下列方式修正：

①對先后順序關系簇任務集合，直接按先后順序展開組成箱任務序列，找到其箱序列編碼中的位置直接替換；

②對不同時的簇任務集合，先找出其在簇序列中的先后位置，并按位置先后展開組成箱任務序列，再找其在箱序列編碼中的位置并替換。

步驟3重復上述兩步修復策略，直到新的箱任務序列不再變化為止。

對種群中重復序列的修正策略：由于算法內外層任務均采取統一編碼方式，在種群中會不可避免地產生重復的個體，不利于算法收斂精度，因此搜尋每代的重復個體，并采用部分逆反變異操作生成新的個體替換原染色體，得到新的種群作為下一代。這樣不僅能降低重復個體存在的概率，而且能保持種群多樣性。endprint

3.3集成調度的啟發式策略

本文算法設計思想是將遺傳算法與有效的啟發式策略相結合，將由內外層編碼得到的可行序列作為任務選擇QC或AGV，AYC的順序，依此順序采用下面的QC調度策略和AGV，AYC調度策略，逐一為當前任務分配合適的設備，直到所有任務完成分配。

QC調度策略見圖4。

QC調度策略的具體步驟如下：

步驟1初始化船舶開始作業時刻（即靠泊時刻），QC的位置和可用時間，簇任務在船上的貝位、任務量和相關約束。

步驟2若可用QC數大于或等于船舶作業QC最小數，則隨機選擇一組連續的QC分配給船舶，轉步驟3；否則推遲船舶開始作業時刻。

步驟3考慮QC和任務屬性，逐一為簇任務n分配作業QC。首先檢查簇任務n左右兩側距其最近的QC，若需要等待時間相同則優先選擇距離更近的QC，若需要等待時間不同則選擇等待時間較短的QC，并更新簇任務n的開始作業和結束作業時刻以及QC位置和再次空閑時刻。

步驟4如此循環執行步驟3，為簇任務n+1分配QC，直到為所有簇任務分配QC完畢，得到QC分配和調度簇任務序列。

AYC調度策略：在給定QC作業箱任務順序后，AYC的作業序列與QC作業序列一致。

LAGV調度策略：根據箱任務序列對LAGV進行運輸任務指派，采用以下啟發式規則對LAGV進行調度：①遵循QC作業順序優先原則；②先到先指派。

3.4適應值函數選擇

適應值函數由目標函數加權和的倒數確定。外層為船舶在港時間（箱任務最大完成時刻）與QC移動距離的歸一化加權和倒數；內層為箱任務最遲結束時刻、每臺QC的箱任務均衡程度、QC總延遲時間、LAGV的總運行時間和AYC總移動時間的歸一化加權和倒數。

3.5選擇、交叉、變異

采用輪盤賭方法對染色體進行選擇；采用部分匹配交叉（圖5）和部分逆反變異（圖6）的方法對染色體進行操作。

4算例分析

4.1案例說明

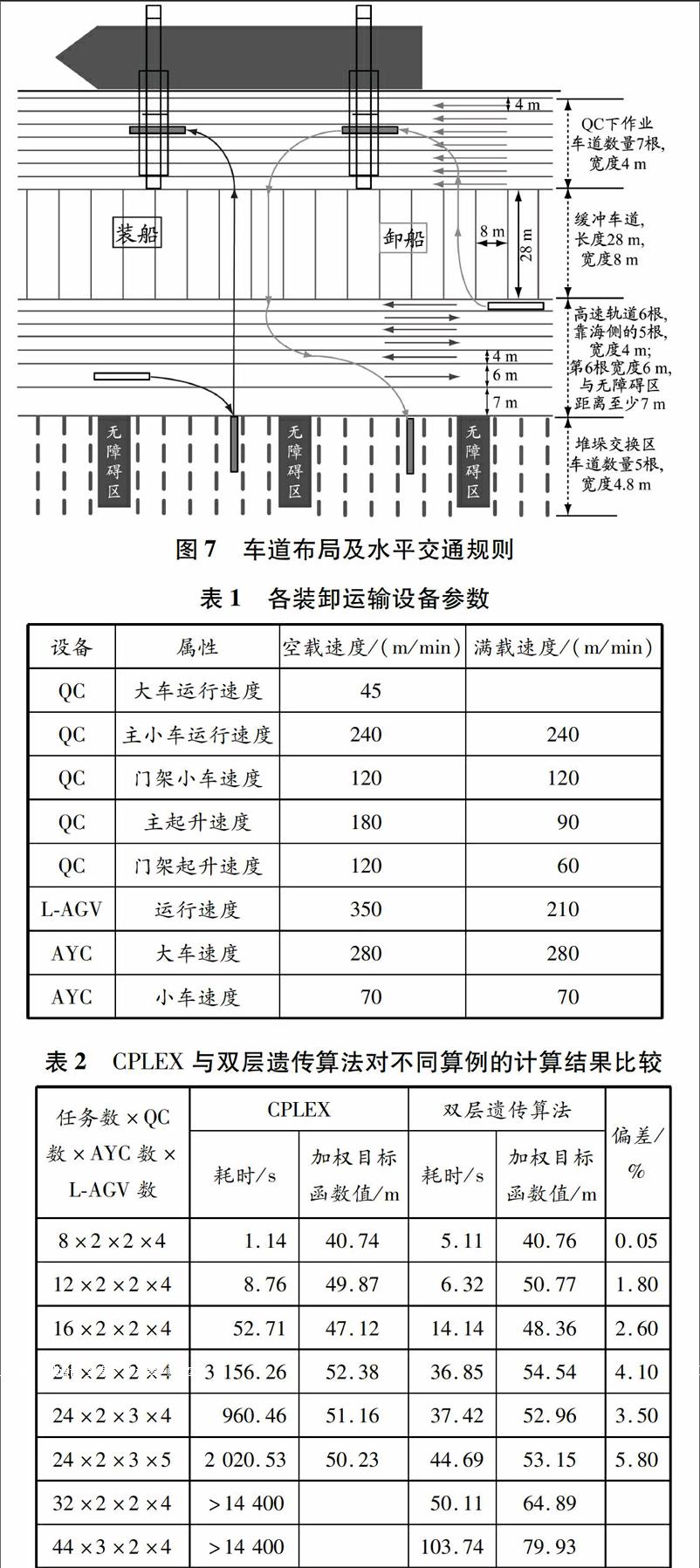
以采用新工藝的青島某自動化碼頭為例。該碼頭總岸線長2 088 m，每個40英尺集裝箱貝位在岸線上跨度為12 m，碼頭共有7臺QC可供分配，假定QC初始位置均勻分布于碼頭岸線上。堆場采用垂直岸線布置，本案例涉及8個箱區，每個箱區配備兩臺AYC，岸側場橋負責裝卸船的存取箱，陸側場橋負責配合外部集卡集疏港，各箱區岸側均設置一組支架的交換區。設置支架數量為5條，并預留一條無支架裝卸車道。水平交通組織中的各類車道數量和寬度是根據QC后伸距以及LAGV參數設定的，車道布局見圖7。QC下裝卸車道為單行道，行車方向是依據船頭朝向和裝卸箱量的比例設定的，以減少倒箱門現象對車輛和道路的干擾。緩沖車道允許雙向行駛，以縮短車輛在岸邊與堆場之間的運行距離；高速相鄰車道行駛方向相反，便于車輛在箱區岸側交換區的進出，水平交通規則見圖7。

假設各AYC和LAGV初始位置均設置在各箱區支架交換區。各設備完成其所有作業后回到初始位置，各裝卸運輸設備參數見表1。QC平均作業效率每小時不低于36個循環，假設QC抓/放箱操作時間均為10 s，QC小車在QC交換區與船舶之間的平均水平運行時間為40 s。某艘船停靠在距岸線100 m處，靠泊時刻為計劃期的第60 min，隨機生成該船需要裝卸作業的簇任務以及箱任務，包括任務數量、在船上和堆場中的位置、各任務之間不同時、

有先后順序等的約束關系。

4.2試驗分析

本文算法采用MATLAB R2012b編程實現，并在Intel（R） Core（TM） 2Quad CPU Q9500 @2.83 GHz處理器，RAM 2GB電腦上運行。通過多次初步試驗確定有關的參數：（1）外層。種群大小50；最大遺傳代數100；交叉概率0.85；變異概率0.10。（2）內層。種群大小50；最大遺傳代數100；交叉概率0.80；變異概率0.05。

為了評估新工藝的集成調度模型和算法，首先設計8組中等規模仿真算例驗證所提算法的性能。為實現建模與算法的分離，將模型的非線性約束轉換成線性約束，采用MATLAB中的YALMIP工具箱結合CPLEX12.2求解器，求解QC調度模型，其中計劃期的時間單位設置成所有簇任務的裝卸時間需求最小值，再根據QC調度結果求解自動化設備集成調度模型。表2最后一列顯示了本文算法的加權目標函數值與最優值之間的偏差。試驗發現，CPLEX的計算耗時隨著任務數的增加快速上升，30個以上箱任務的問題無法在有效的時間內得到結果（最后兩組算例的時間都超過了4 h），而雙層遺傳算法盡管不能獲得最優解，但在大規模任務的計算效率上具有優勢。

為分析系統的靈敏性，選取LAGV數和計劃期長度（任務數）作為變化因素，試驗結果見圖8。可以看出，在給定LAGV數的條件下，加權目標函數值隨著計劃期長度的增加而增加，但任務的平均值在下降。這表明，計劃期越長，系統越能獲得更好的性能。然而計算更多任務數將花費更多時間。在實際中，由于碼頭各種中斷事件的發生，如起重機或AGV等設備故障，會不可避免地需要進行再調度。因此，可以結合實際情況，選取一個適當的計劃期以權衡計算量和系統性能的損失。此外，在給定計劃期的條件下，LAGV數會影響系統性能，特別是對某具體算例，存在最優的數量配置。決定加權目標函數值變化的因素除LAGV數外，還包括任務的信息及其在QC上的序列。

為分析集成調度的效果，采用雙層遺傳算法，模擬3臺QC，8輛LAGV，8臺AYC，10個簇任務，44個裝卸箱任務條件下各設備作業序列的優化。圖9呈現了QC理想調度（QC無等待）與集成調度得到的各QC任務的開始和結束時刻（圖9a）中矩形塊為簇任務編號，圖9b）中矩形塊為箱任務編號）。

圖9a）顯示在集成調度的情況下，各QC作業比較均衡并均存在等待，說明LAGV和AYC的調度影響了QC調度結果；較單環節調度，集成調度協調了各環節之間的沖突，對碼頭資源整合有重要借鑒作用。圖9b）顯示QC累積等待時間在各QC之間分endprint

配的非均衡性，因為LAGV和AYC的調度目標之一是在最小化船舶在港時間的情況下使各QC任務完成時間盡量均衡，減少任務多的QC的作業延遲。

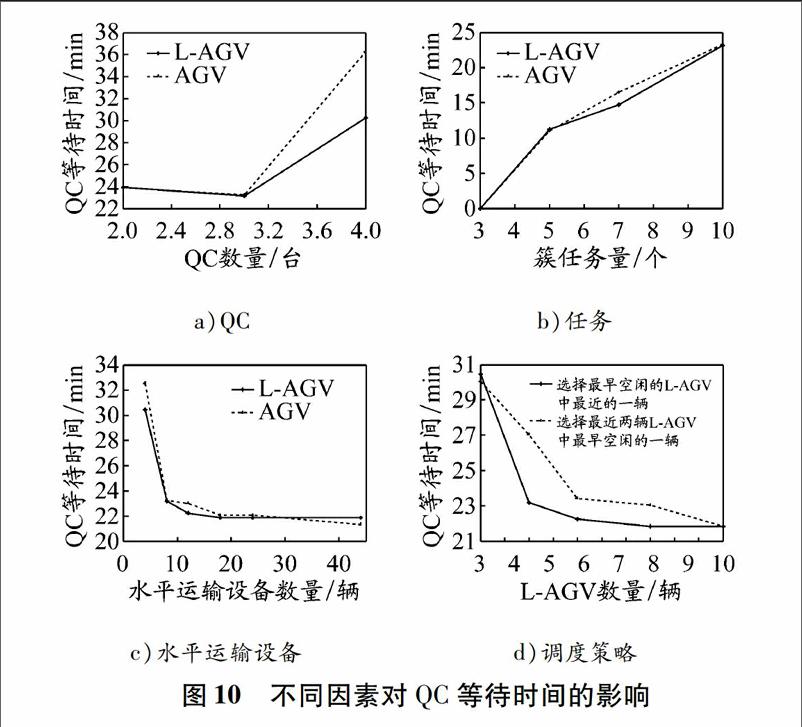
選擇3種變化因素對比在新工藝“LAGV+支架”與傳統AGV工藝下集成調度的結果。第1個因素是QC數量，設定為2，3，4；第2個因素是簇任務規模，設定為3，5，7，10；第3個因素是水平運輸設備的數量，設定為4，8，12，18，24，44。此外，比較了兩種常見LAGV調度策略的影響。每種組合試驗次數為10次，試驗結果見圖10。

a）QC

b）任務

c）水平運輸設備

d）調度策略

由圖10a）可知：當QC和（L）AGV的配置比例增大時，采用“LAGV+支架”工藝較采用AGV可明顯降低QC等待時間；當該比例減少時，“LAGV+支架”工藝的緩沖作用發揮不明顯，QC等待時間差別不大。

由圖10b）可知：兩種工藝下的QC等待時間均隨著任務規模增大而增加，采用“LAGV+支架”工藝較采用AGV的QC等待時間短；在設備配置一定的情況下，當任務規模為中等時，采用“LAGV+支架”工藝較AGV工藝的優勢更明顯。

由圖10c）可知：當水平運輸設備不夠充足時，兩種工藝下的QC等待時間均隨著（L）AGV數量的增加而減少；“LAGV+支架”工藝下的QC等待時間比相應的AGV工藝下的QC等待時間短。但是，隨著（L）AGV數量繼續增加，QC等待時間趨于穩定。在水平運輸設備不充足的情況下，采用“LAGV+支架”工藝較AGV工藝有更明顯的優勢。

由圖10d）可知：在縮短QC等待時間上，本文算法采用的策略a（選擇最早空閑的最近的一輛LAGV完成待作業任務）較策略b（選擇最近兩輛LAGV中最早到達的一輛LAGV完成待作業任務）具有明顯優勢。分析可知，采用策略b一方面會導致緊急任務得不到及時作業，另一方面會導致某些LAGV處于閑置狀態，水平運輸設備任務量不均衡，進而導致QC等待時間過長。

5結束語

考慮碼頭裝卸作業各環節和緩沖系統的調度，以最小化船舶在港時間為整體目標，建立了自動化設備集成調度框架和相關模型。設計了雙層遺傳算法結合啟發式策略對模型進行求解。結果表明：設備協同調度較單環節獨立調度能改善岸橋（QC）調度均衡性；“支架+自帶提升功能的自動導引小車（LAGV）”工藝在中等任務規模、QC與車輛配比較大條件下，具有明顯的優勢。研究結果可為碼頭設備的調度提供重要的決策支持。下一步的研究工作中將會考慮LAGV路徑規劃和能量約束的影響。

參考文獻：

[1]KIM Jeongmin， CHOE Ri， RYU Kwang Ryel. Multiobjective optimization of dispatching strategies for situationadaptive AGV operation in an automated container terminal[C]//Research in Adaptive and Convergent Systems. ACM， 2013： 16.

[2]樂美龍， 趙彥營， 劉秀玲. 時間窗下單船岸橋調度[J]. 計算機工程與應用， 2014， 50（9）： 242248.

[3]HE Junliang， HUANG Youfang， YAN Wei. Yard crane scheduling in a container terminal for the tradeoff between efficiency and energy consumption[J]. Advanced Engineering Informatics， 2015， 29（1）： 5975.

[4]秦天保， 彭嘉瑤， 沙梅. 帶任務順序約束的岸橋集卡集成調度約束規劃模型[J]. 上海海事大學學報， 2013， 34（3）： 17.

[5]馬超， 梁承姬. 集裝箱碼頭岸橋分配與集卡調度整合問題研究[J]. 廣西大學學報（自然科學版）， 2015， 40（3）： 643650.

[6]CHEN Lu， LANGEVIN Andre， LU Zhiqiang. Integrated scheduling of crane handling and truck transportation in a maritime container terminal[J]. European Journal of Operational Research， 2013， 225（1）： 142152.

[7]錢繼鋒. 集裝箱碼頭“岸橋集卡堆場”作業計劃的優化[D]. 北京： 北京交通大學， 2014.

[8]DKHIL Hamdi， YASSINE Adnan， CHABCHOUB Habib. Optimization and simulation of container handling systems in automated maritime terminal[J]. Studies in Computational Intelligence， 2013， 457： 301312.

[9]樂美龍， 張清波. 自動化碼頭橋吊、自動引導車以及龍門吊的聯合調度[J]. 青島科技大學學報（自然科學版）， 2015， 36（5）： 569574.

[10]宓為建， 李央央， 胡鴻韜. 集裝箱堆場分配與自動化裝載小車路徑聯合優化[J]. 上海海事大學學報， 2015， 36（4）： 1621.

[11]湯鵬飛， 梁承姬， 丁一， 等. 考慮岸橋緩存區的ALV調度優化問題研究[J]. 廣西大學學報（自然科學版）， 2015， 40（6）： 15401550.

[12]余孟齊， 韓曉龍. 有限緩沖空間下岸橋和自動升降車的集成調度[J]. 武漢理工大學學報（信息與管理工程版）， 2016， 38（1）： 101105.

[13]BIERWIRTH C， MEISEL F. A survey of berth allocation and quay crane scheduling problems in container terminals[J]. European Journal of Operational Research， 2010， 202（3）： 615627.

（編輯賈裙平）endprint