基于LuGre摩擦模型的轉臺伺服系統自適應摩擦補償研究

郭遠韜，閔 斌，陳 斌

(1.上海航天控制技術研究所,上海 201109； 2.上海航天技術研究院，上海 201109)

基于LuGre摩擦模型的轉臺伺服系統自適應摩擦補償研究

郭遠韜1，閔 斌2，陳 斌1

(1.上海航天控制技術研究所,上海 201109； 2.上海航天技術研究院，上海 201109)

為消除非線性摩擦對測試轉臺性能的影響，選用LuGre摩擦模型描述轉臺系統所受的非線性摩擦。根據轉臺直流電機系統數學描述，提出了非線性摩擦補償方法。設計了雙觀測器結構估計LuGre模型中的不可測狀態；考慮LuGre模型中3個參數的非一致性變化，設計了自適應摩擦補償控制算法，在線估計摩擦模型中的參數，并對非線性摩擦進行補償。用李雅普諾夫方法證明了采用自適應摩擦補償方法的閉環系統的穩定性。仿真結果表明：正弦波輸入時，摩擦補償后的位置跟蹤誤差(峰-峰值)較無摩擦補償減小了1個量級，位置跟蹤性能有較大改善，辨識出的摩擦模型參數能穩定收斂于真實值附近；三角波輸入時，自適應控制的位置跟蹤精度更高。

測試轉臺； LuGre摩擦模型； 非線性摩擦； 不可測狀態； 雙觀測器結構； 自適應摩擦補償； 穩定性； 位置跟蹤

0 引言

高精度測試轉臺是檢測和評價慣性導航與制導系統的主要設備，利用高精度測試轉臺對陀螺儀和加速度計進行研究，建立其數學模型，鑒定其精度等級，通過不同的試驗方法確定被測儀表的各種誤差因素，可對其進行補償以提高整個慣導系統的精度。因此，測試轉臺的優劣直接關系測試試驗的可靠性和置信度，是保證航空航天產品和武器系統精度及性能的基礎，對航空、航天工業和國防建設有重要意義。摩擦力是影響測試轉臺精度的一個重要因素，它具非線性，常會導致轉臺伺服系統出現穩態誤差、極限環和低速爬行等問題。為提高轉臺的精度，須采取合理的摩擦補償方法降低或消除非線性摩擦對轉臺伺服系統的影響。摩擦補償方法有多種，根據其是否需要具體的摩擦模型，可分為非模型的和基于模型的兩種。對非模型補償，可采用傳統PID/PD控制器，但不能滿足高精度位置跟蹤需求，也易造成系統出現極限環振蕩，或將摩擦力矩干擾等效為不確定周期擾動，通過設計魯棒控制器予以克服[1]。此外，還可采用神經網絡控制和模糊邏輯控制等摩擦補償方法[2-3]。基于模型的補償方法通常是在線估計摩擦模型的參數，將一個摩擦補償項加入標準的控制算法對摩擦進行補償[4-6]。基于摩擦模型的補償方法取決于摩擦模型的選擇，摩擦模型越能真實反映摩擦的動靜態特性，摩擦的補償效果就越好。摩擦的數學模型有庫倫摩擦模型、Stribeck摩擦模型、Karnopp摩擦模型等多種形式，但上述模型均屬于靜態模型，不能正確描述摩擦的動態特性，如臨界摩擦力、摩擦滯后、預滑動位移和摩擦滯回等現象[7-8]。1968年，DAHL提出了Dahl摩擦模型，通過引入一個內部狀態變量，反映摩擦的記憶現象。WIT等在Dahl模型的基礎上提出了LuGre摩擦模型，賦予狀態變量確切的物理含義，使其模型不但可描述增加的靜摩擦力及摩擦記憶現象，而且能描述Stribeck曲線，是目前較完善的一個模型。本文基于LuGre摩擦模型設計自適應摩擦補償算法，基于LuGre摩擦模型中的狀態變量無法直接測得，設計兩個狀態觀測器，觀測摩擦模型中的狀態變量，辨識出摩擦模型系數并進行補償。

1 摩擦模型建立

LuGre摩擦模型將產生摩擦的接觸面視為有大量隨機行為的鬃毛，當有切向作用力時，鬃毛像彈簧般變形產生摩擦力，模型通過鬃毛接觸點形成、鬃毛變形、接觸點斷開，以及新接觸點形成的過程描述摩擦的動態行為[9-10]。鬃毛的平均形變可用z表示，有

(1)

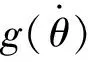
(2)

式中：Fc為庫倫摩擦力；Fs為最大靜摩擦力；ωs為Stribeck速度。則由鬃毛產生的摩擦力加上黏性摩擦，總摩擦力

(3)

式中：σ0，σ1，σ2分別為鬃毛剛性系數、滑動阻尼系數和黏性摩擦因數，這些參數會在外界溫度、潤滑條件、材料磨損及接觸面作用力等因素的影響下發生改變[11-12]。

2 摩擦補償方法設計

2.1 轉臺直流電機系統數學描述

在機械軸承轉臺的位置控制中，通常采用永磁直流力矩電機作為其驅動裝置，因其除普通電勵磁直流電機具備的調速范圍寬和便于控制等特點外，還有體積小、效率高、用銅量少、結構簡單和運行可靠等優點。經適當簡化，永磁直流力矩電機的傳遞函數如圖1所示。圖1中：La為電機電樞電感；Ra為電機電樞電阻；Ki為電機力矩系數；Ke為電機反電勢系數；J為電機包括負載在內的轉動慣量；Mfric為系統所受摩擦力矩；u為控制輸入。

由圖1可得微分方程

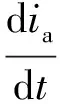
(4)

(5)

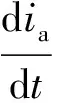
(6)

令a=JRa/Ki，b=-Ke，則式(6)可寫為

(7)

轉臺的控制系統一般由電流環、速度環和位置環構成。電流環和速度環的作用是提高系統的剛度以抑制系統的非線性及外部擾動，控制系統的精度主要由位置環保證。工程實踐中常用PID控制器調節位置環的性能，但常規PID控制往往不能消除非線性摩擦對系統的影響，因此需設計控制算法補償非線性摩擦，提高轉臺系統的精度。

2.2 非線性摩擦補償方法設計

因LuGre摩擦模型中的參數σ0，σ1，σ2會受溫度和材料磨損等外界因素影響發生變化，故需用自適應控制算法在線辨識出后，再對非線性摩擦進行補償[9]。

帶摩擦的伺服系統微分方程可簡化為

(8)

將式(3)中的摩擦模型代入式(8)，可得

(9)

將式(1)代入式(9)，得

(10)

式中：β=σ1+σ2>0。

引入誤差項

e=θ-θr

(11)

(12)

式中：λ為大于0的常數；θr為期望位置信號。當ε很小或指數收斂到0時，e也會收斂到0。則可得

(13)

為獲得摩擦模型中的z，設計兩個閉環觀測器為

(14)

(15)

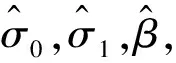
(16)

將控制率式(16)代入式(13)，則有

(17)

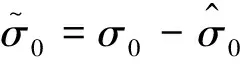
用基于李雅普諾夫函數方法證明上述基于雙觀測器結構的自適應摩擦補償方法的閉環穩定性。建立李雅普諾夫函數

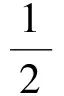
(18)

式中：r0，r1，r2為自適應增益，均為大于0的常數，由設計者選取。對式(18)李雅普諾夫函數沿式(13)～(15)微分，可得

(19)

選擇參數估計值和觀測器補償項為

(20)

(21)

(22)

τ0=-ε

(23)

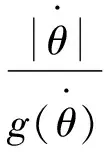
(24)

用上述更新率后李雅普諾夫函數的導數

(25)

3 仿真與分析

在Matlab/Simulink仿真環境中對上述自適應摩擦補償方法進行仿真研究。選擇某測試轉臺的直流力矩電機系統參數和LuGre摩擦模型參數為：a=0.25；b=-2.5；σ0=9.8 N·m/rad；σ1=5.8 N·m·s/rad；β=5.87 N·m·s/rad；Mc=0.12 N·m；M1=0.033 N·m；ω1=0.001 rad/s。分別比較單PID控制率和補償后的PID控制率。

考慮正弦波輸入，給定輸入位置信號θr=0.5sin(πt)，取控制增益和自適應增益為λ=300，k=300，r0=2 000，r1=4 000，r2=2 000，無/有自適應控制率的位置跟蹤誤差結果分別如圖2、3所示，有自適應控制率的摩擦參數估計結果如圖4所示。

由圖2、3可知：加入摩擦補償后的位置跟蹤誤差(峰-峰值)較無摩擦補償減小了1個量級，位置跟蹤性能有較大改善。由圖4可知：辨識出的摩擦模型參數都穩定收斂于真實值附近。仿真結果表明：當非線性摩擦力模型中參數發生非一致性變化時，用本文的自適應補償方法能準確辨識出摩擦力參數，并對非線性摩擦進行補償，明顯改善了轉臺系統的位置跟蹤性能。

考慮三角波輸入，以周期10 s、速度幅值0.000 5 rad/s的三角波作為輸入，比較兩種控制方法的位置跟蹤誤差，所得PID控制器和自適應控制的位置跟蹤誤差分別如圖5、6所示。

由圖5、6可知：在三角波輸入下，采用PID控制的轉臺系統位置跟蹤誤差為1.5×10-5rad(峰-峰值)，采用自適應控制的轉臺系統位置跟蹤誤差為6×10-8rad(峰-峰值)，自適應控制的位置跟蹤精度更高。

4 結束語

本文分析了轉臺伺服系統中的非線性摩擦及其對系統的影響。考慮LuGre模型中存在不可測的狀態，設計了雙觀測器結構估計摩擦模型中的不可測狀態，再考慮LuGre摩擦模型中的三個參數產生非一致性變化的情況下，用李雅普諾夫穩定性分析方法設計了自適應摩擦補償控制算法，在線估計出摩擦模型中的參數，并對非線性摩擦進行補償。仿真結果顯示：用本方法可明顯改善轉臺伺服系統的位置跟蹤性能，并能動態辨識出摩擦模型參數，證實了本方法的有效性。本方法選用的LuGre模型較其他模型能更真實地反映轉臺運動過程中的摩擦力，由在線估測使LuGre模型實時更新狀態，進一步提高了模型本身的準確度，控制方法對提高轉臺位置精度指標有實際應用價值。

[1] 王本永. 基于H∞控制理論的液壓三軸仿真轉臺控制系統研究[D]. 哈爾濱: 哈爾濱工業大學, 2008.

[2] SELMIC R R, LEWIS F L. Netural network approximation of piecewise continuous functions: application to friction compensation[J]. IEEE Transactions on Neural Networks, 2002, 13(3): 745-751.

[3] 王永富, 柴天佑. 一種補償動態摩擦的自適應模糊控制方法[J]. 中國機電工程學報, 2005, 25(2): 139-143.

[4] YAZDIZADEH A, KHORASANI K. Adaptive friction compensation based on the Lyapunov scheme[C]// IEEE International Conference on Control Applications. Dearborn: IEEE, 1996: 1060-1065.

[5] VEDAGARBHA P, MDAWSON D. Tracking Control of mechanical systems in the presence of nonlinear dynamic friction effects[J]. IEEE Transactions on Control Systems Technology, 1999, 7(4): 446-456.

[6] 王忠山. 高精度機械軸承轉臺摩擦補償研究[D]. 哈爾濱: 哈爾濱工業大學, 2007.

[7] WIT C D. A new model for control of systems with friction[C]// IEEE Transactions on Automatic Control. Houston: IEEE, 1995: 419-425.

[8] TAN Y, KANELLAKOPOULOS I. Adaptive nonlinear friction compensation with parametric uncertainties[C]// American Control Conference. Washington D. C.: [s. n.], 1999: 2511-2515.

[9] 王瑞娟, 梅志千, 李向國. 機電伺服系統非線性摩擦自適應補償的研究[J]. 中國電機工程學報, 2012, 32(36): 123-128.

[10] 王英, 熊振華, 丁漢. 基于狀態觀測的自適應摩擦力補償的高精度控制[J]. 自然科學進展, 2005, 15(9): 1100-1105.

[11] 周金柱, 段寶巖, 黃進. LuGre摩擦模型對伺服系統的影響與補償[J]. 控制理論與應用, 2008, 25(6): 990-994.

[12] TAN Y, TAN H. Adaptive backstepping control and friction compensation for AC servo with inertia and load uncertainties[J]. IEEE Transactions on Industrial Electronics, 2003, 50(5): 944-953.

StudyonAdaptiveFrictionCompensationofTurntableServoSystemsBasedonLuGreFrictionModel

GUO Yuan-tao1， MIN Bin2， CHEN Bin1

(1. Shanghai Institute of Spaceflight Control Technology, Shanghai 201109, China;2. Shanghai Academy of Spaceflight Technology, Shanghai 201109, China)

To eliminate the effect of nonlinear friction on test turntable, LuGre friction model was selected to describe nonlinear friction of the test turntable. According to the mathe description of the DC motor system, the method to compensate the nonlinear friction was put forward. The dual-observer was designed to estimate the unmeasurable state in the LuGre friction. Taking into account the occurrence of 3 non-uniform parameters change in LuGre friction model, the control algorithm with adaptive friction compensation was designed, which estimated the parameters in the friction model on line and compensate the nonlinear friction. The system stability of the closed-loop with adaptive friction compensation was proved by Lyapunov approach. The simulation results showed that the position tracking error (peak-peak) with compensation was 1 order smaller than the one without compensation and the performance of the position tracking was improved greatly as well as the estimated parameters of the friction model were converged to around the true value for sinusoidal input. The accuracy of the position tracking with adaptive control was much higher for triangular waveform input.

test turntable; LuGre friction model; nonlinear friction; unmeasurable state; dual-observer; adaptive friction compensation; stability; position tracking

2017-08-19；

2017-10-22

郭遠韜(1989—)，男，碩士，主要研究方向為伺服系統摩擦補償。

1006-1630(2017)06-0065-05

TM921.54

A

10.19328/j.cnki.1006-1630.2017.06.010