一種子陣級DAR同時多波束擬合測角方法

((中國航空工業集團公司雷華電子技術研究所,江蘇無錫214063)

一種子陣級DAR同時多波束擬合測角方法

劉洋濤,李曉明,曹書華

((中國航空工業集團公司雷華電子技術研究所,江蘇無錫214063)

針對數字同時多波束技術在子陣級數字陣列雷達中的應用問題,提出了一種適用于子陣級數字陣列雷達的同時多波束測角方法。首先介紹了如何通過數字加權的方式形成同時接收多波束,然后基于比幅法建立了同時多波束擬合測角模型,給出了同時多波束擬合測角方法的實現流程和具體步驟,最后進行仿真驗證及分析。仿真結果表明:該方法具有與數字和差單脈沖相當的測角精度,且在保持一定測角精度的情況下,同時多波束擬合測角方法可以獲得更寬的測角范圍,具有良好的工程化應用價值。

數字陣列雷達;同時多波束;擬合測角;單脈沖測角;工程化應用

0 引 言

近年來,子陣級數字陣列雷達(DAR)技術由于其靈活的數字波束形成技術得到快速發展和應用。子陣級數字陣列雷達具有同時多波束[1]形成能力,與常規的單個接收波束相比,同時接收多波束處理可以降低空域搜索時間,充分利用發射波束能量,降低波束跨越損耗,提高雷達的平均作用距離。

與常規機載相控陣雷達[2]不同的是,子陣級數字陣列雷達不僅可以采用數字和差單脈沖技術,還能采用同時接收多波束測角技術,其優勢在于:一是與數字和差單脈沖測角[3]精度基本相當;二是可以擴大瞬時測角范圍,有利于雷達大范圍搜索或目標丟失重照時快速捕獲目標。數字同時多波束技術目前在地基雷達中已經得到廣泛應用,在機載雷達中也逐步得到了應用。

檢索相關文獻后發現,有一些針對數字多波束形成技術進行討論的文獻,但具體到針對數字同時多波束測角的文獻鮮有報道。Kai-Bor Yu[4-5]提到同時5個波束形成及其單脈沖斜率曲線的粗略討論,李杰濤等[6]針對一維相控陣雷達研究了一維同時多波束測角方法。本文針對二維子陣級數字陣列雷達研究了一種同時多波束擬合測角算法。

本文首先介紹二維同時接收多波束形成方法,然后給出同時多波束測角方法原理和實現流程,最后進行仿真驗證,并與數字和差單脈沖測角進行性能對比,仿真結果驗證了該方法的正確性和有效性,可以為同時多波束測角算法工程化設計提供參考。

1 數字同時接收多波束形成

數字同時接收多波束形成主要有兩種實現方法[7]:一種是直接對子陣通道采樣數據直接加權進行N組分別加權,同時形成N個波束;另外一種是對子陣通道采樣數據進行N點FFT變換形成N個波束。采用分別加權的方法靈活性大,各個波束最大值方向可以任意選取,靈活性好。采用FFT方法運算量小,便于硬件模塊化實現,但是該方法各個波束最大值之間的間距不能改變,靈活性較差。方法一原理簡圖如圖1所示。

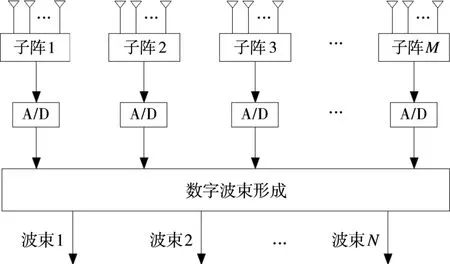
圖1 分別加權同時多波束形成示意圖

為了要形成第k個接收波束(其接收波束的指向為θBk),則對各個接收波束應分別提供該接收波束所需要的“陣內相位差”。

對于二維陣面,以形成第k個接收波束為例,應提供的天線陣內相位誤差補償值為

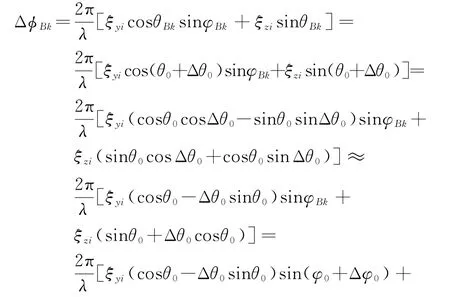
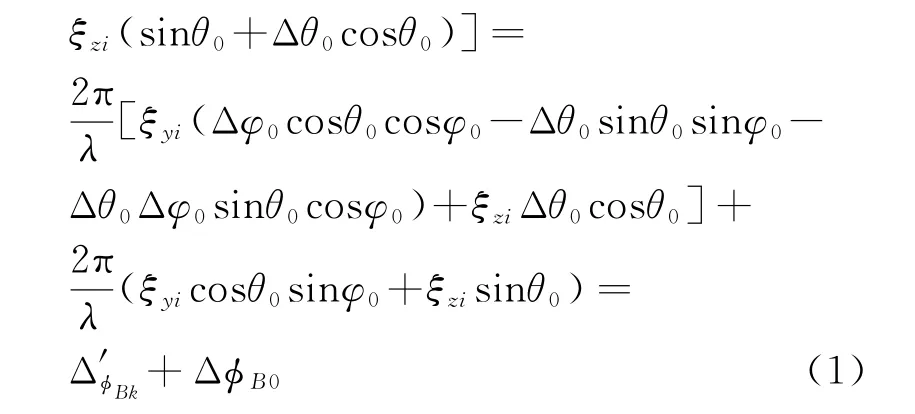
式中,

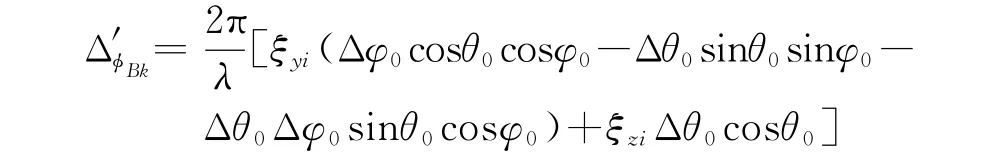
定義式(1)中(ξyi,ξzi)為第i個子陣相位中心坐標,式中利用 Δθ0?1且Δφ0?1時,有cosΔθ0≈1,cosΔφ0≈1,sinΔθ0≈Δθ0,sinΔφ0≈Δφ0,Δ?B0由子陣延時單元和移相器提供,剩余部分由數字加權補償。根據當前波束指向俯仰角θ0、方位角φ0,以Δθ0,Δφ0為波束間隔計算第k個接收波束形成權向量W=ae-jΔ,a=[a1,a2,…,a i,…],其中a i為第i個子陣幅度加權值。

2 同時多波束測角原理及實現

2.1 數字同時多波束測角建模

以三波束為例,建立比幅測角原理圖,如圖2所示,F(θ1),F(θ2)和F(θ3)分別為形成的相鄰三波束功率方向圖,對應各自波束指向方向分別為θ1=θ0-Δθ0,θ2=θ0和θ3=θ0+Δθ0,其中θ0為雷達當前波束中心指向角,Δθ0為波束指向角度偏移量,θT代表目標來波方向。

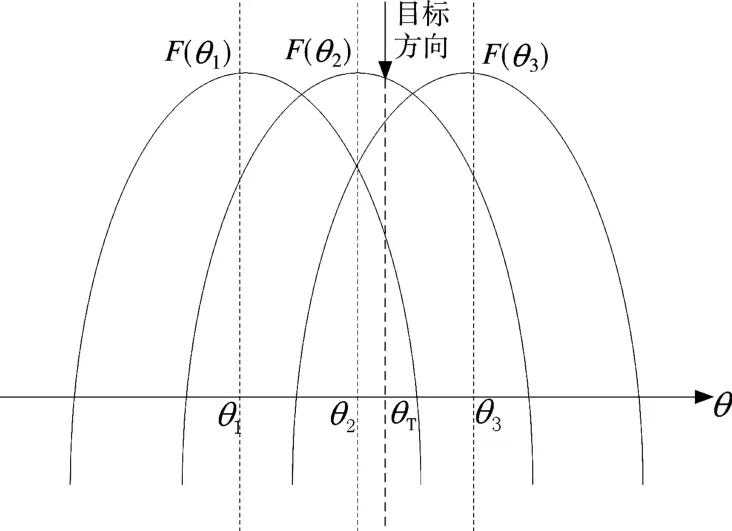
圖2 數字同時多波束測角原理圖

因此可以建立測角模型:

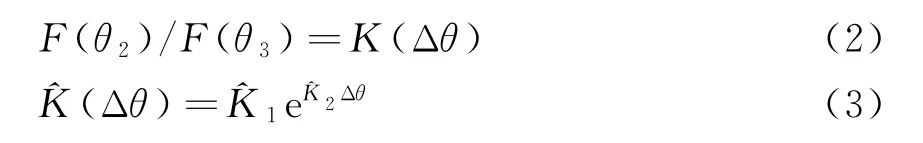
測角原理如下:對3個接收波束功率方向圖,選擇兩個目標方向增益相對較大者(F(θ2)和F(θ3))進行比較(增益大者在前),以Δθ為變量,可以確定一條曲線K(Δθ),該曲線可以用進行擬合近似得到。

雷達接收回波時,對于相鄰三波束,選取兩路目標功率較大者進行比較,可以根據式(2)、式(3)確定相應的進而可以確定目標所在的精確位置。目標角度計算公式如下:

式中,θTemp為目標信號功率最大所在波束號對應的波束指向角。

2.2 實現方法及步驟

圖3示出了單發5收波束示意圖,圖4示出了同時多波束擬合測角實現流程。

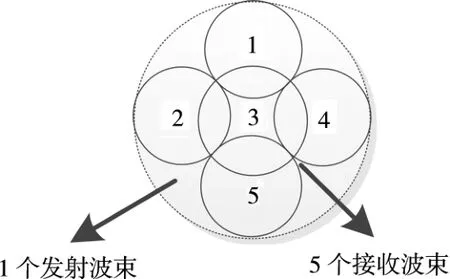
圖3 單發5收波束示意圖

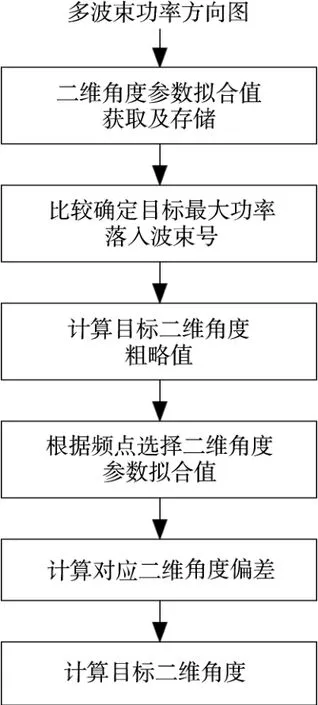
圖4 同時多波束擬合測角實現流程

以方位向三波束測角為例(俯仰向類似),具體步驟如下:

步驟2 重復步驟1獲得不同頻點、不同波束指向角下的角度參數擬合值并進行存儲(頻點間隔、波束指向角步進根據實際測角精度要求確定)。

步驟3 目標落入的主波束號判定。對經過相關處理后同一距離門、頻率門上目標的方位向三路CFAR檢測結果進行功率排序選大,記下功率最大的波束號Num、功率次大的波束號Num1以及對應的目標功率PNum,PNum1;當前雷達中心波束的指向角δ0。

步驟4 計算目標方位角粗略值。根據目標落入的最大的波束號Num對應的方位角偏移ΔδNum計算目標方位角粗略值δrough=δ0+ΔδNum。

步驟5 根據當前雷達載頻利用查表法選擇事先存儲的方位角參數擬合值根據式(2)、式(3),將F(θ2)和F(θ3)分別用PNum,PNum1代替計算方位角誤差

步驟6 根據式(4)計算目標的精確角度值。

3 仿真結果及分析

3.1 仿真條件

設置非均勻64子陣劃分陣面,單個子陣陣元數20～40不等;陣元間距約半波長,X波段載頻。假設子陣級、陣元級兩級幅相誤差均服從均勻分布,設置主要仿真參數如表1所示。

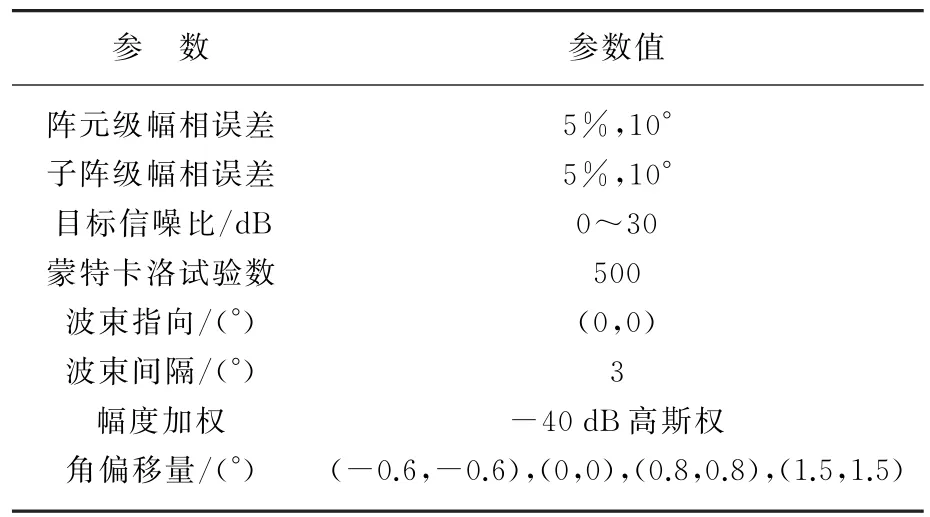
表1 仿真參數表

下面以信噪比作為變量仿真該方法下的測角精度,仿真中以均方根誤差作為測角精度評價指標進行統計分析。

3.2 仿真結果

圖5(a)、(b)分別給出了圖3所示的方位向、俯仰向同時三波束形成示意圖。

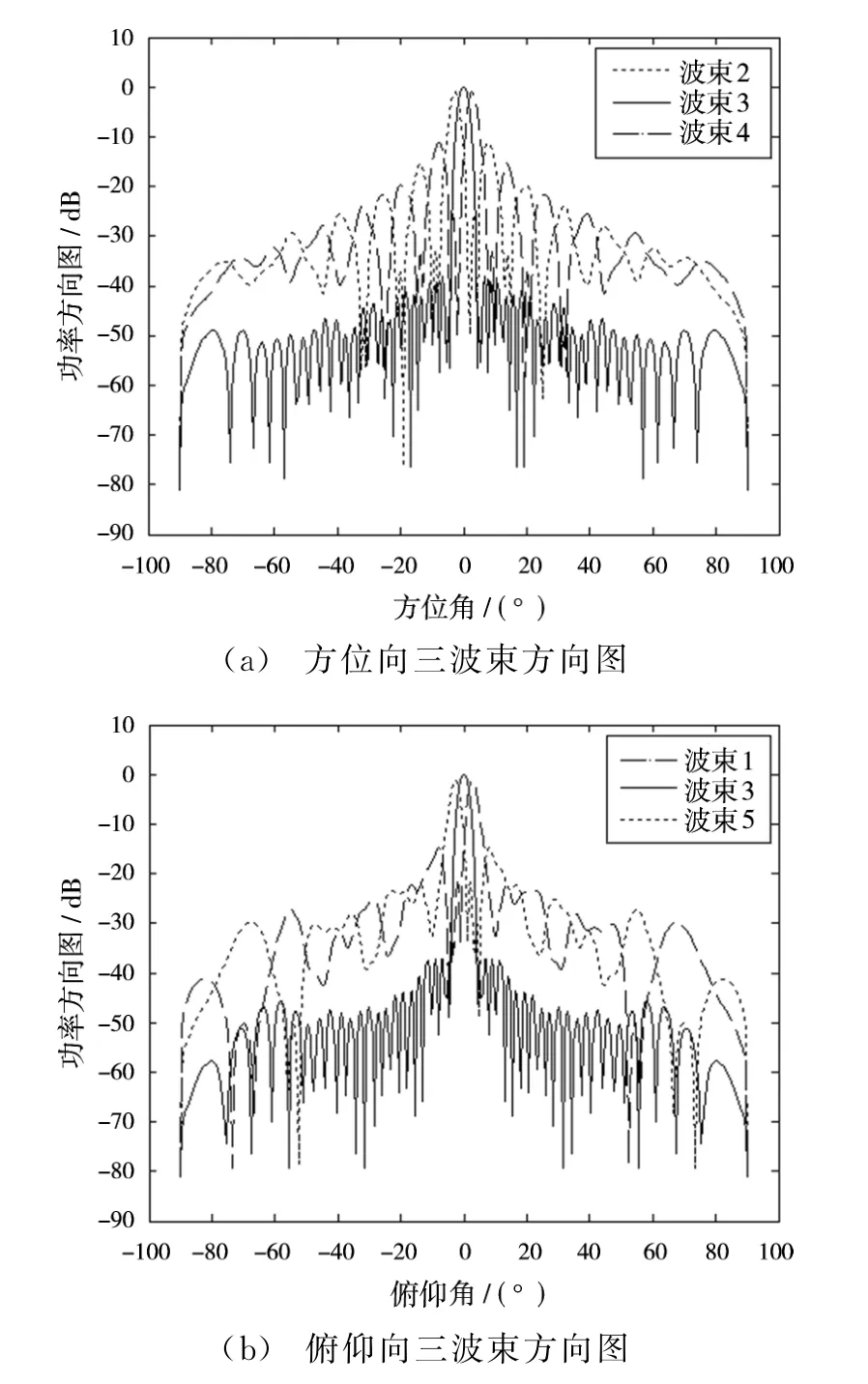
圖5 同時多波束形成方向圖示例

可以看出,中心波束(波束3)第一副瓣約為-40 d B,其余幾個波束的第一副瓣有不同程度的抬高,且波束1,2,4,5增益略低于中心波束。原因是多波束形成過程中的額外加權破壞了原有的幅度權,使得主瓣增益下降,副瓣抬高。

圖6為相鄰兩波束增益比示例圖。可以看到,擬合曲線可以較好地表征實際增益曲線。

圖7為蒙特卡洛實驗仿真結果。結果表明,在其他仿真條件一定的情況下,隨著信噪比由0 dB逐漸增加至30 dB,數字同時接收多波束測角精度逐漸收斂。以信噪比15 dB為例,角偏移量分別為(0°,0°),(0.8°,0.8°)和(1.5°,1.5°)時,方位向測角精度分別可以達到0.12°,0.1°和0.17°,俯仰向測角精度分別可以達到0.12°,0.08°和0.19°。當然,由于擬合偏差的存在,不同角偏移情況下的測角精度也存在一定的差異。當角度偏移較大時,測角誤差也稍偏大。

圖8給出了與數字和差單脈沖測角性能對比結果,仿真中方位、俯仰角度偏移均取-0.6°。

圖8仿真結果表明:在相同仿真條件下,數字同時多波束測角與數字和差測角精度基本相當。在保持一定測角精度的前提下,數字和差法測角范圍只能覆蓋單個波束,而同時多波束擬合測角法可以同時覆蓋多個波束,圖9給出了仍以三波束為例的測角范圍示意圖。

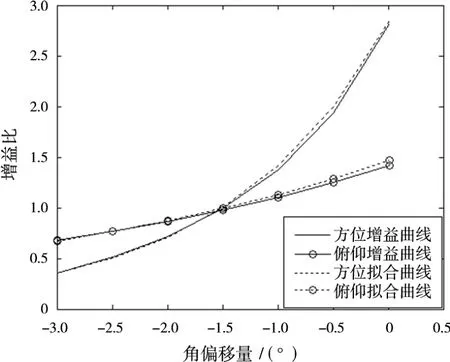
圖6 相鄰兩波束增益比及擬合曲線示例

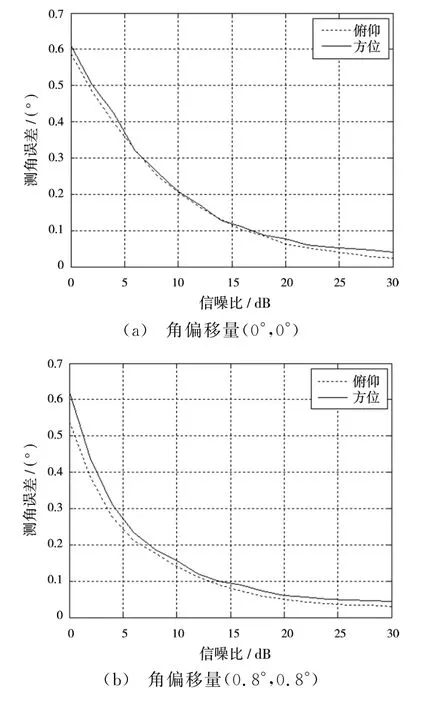
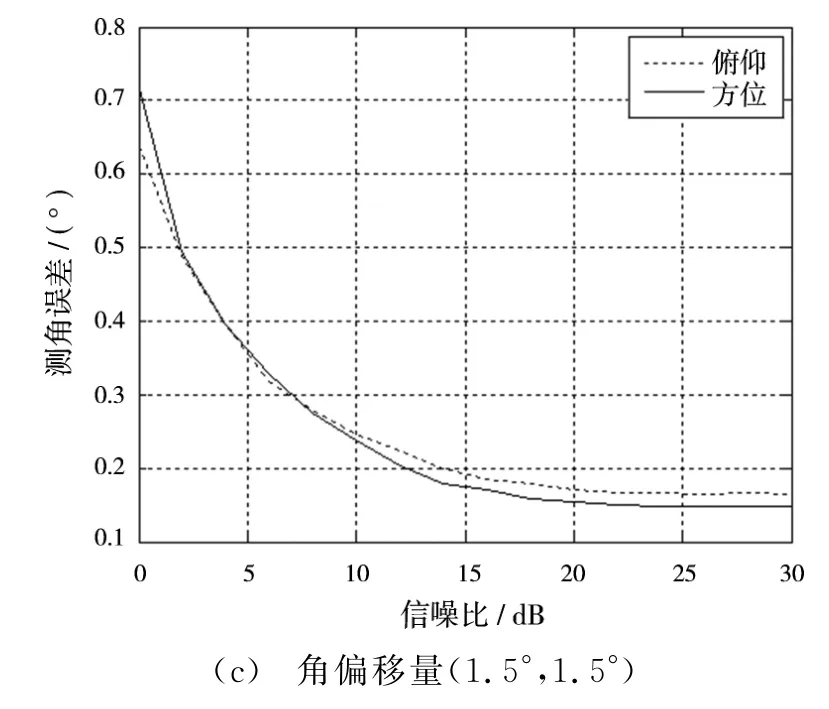
圖7 不同角偏移量下的測角結果示例

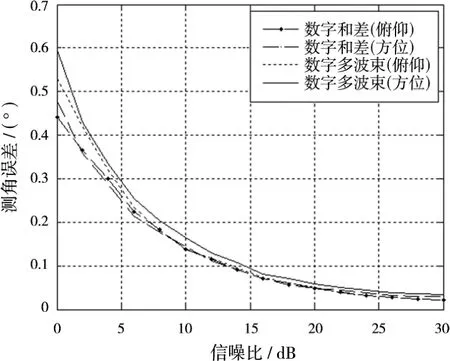
圖8 與數字和差單脈沖測角性能對比

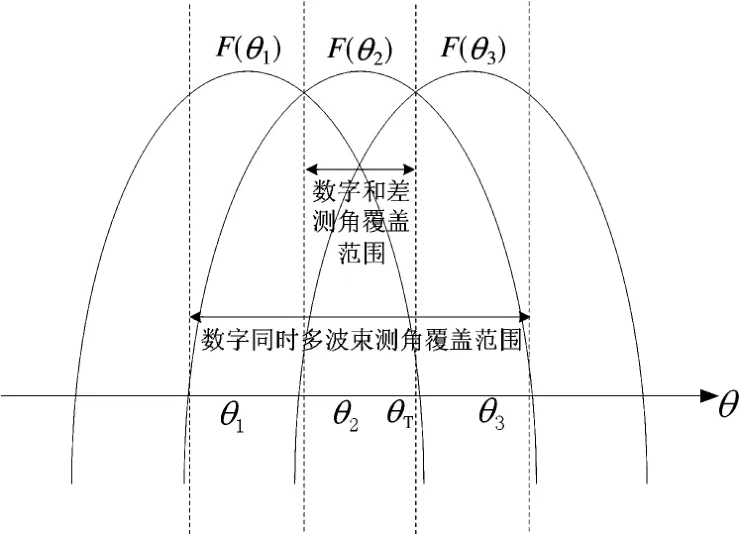
圖9 同時三波束測角范圍示意圖

當然,需要注意的是,兩種方法測角精度是否相當,與波束間隔控制、加權方式選取等影響因素有關。

4 結束語

本文提出了一種基于子陣級數字陣列雷達的同時接收多波束擬合測角方法。首先介紹了數字同時接收多波束形成原理,隨后建立了同時多波束測角模型,給出了具體實現方法及步驟,仿真分析結果表明該方法正確可行,且與數字和差單脈沖測角精度相當,具有較強的工程實用價值。

[1]鄧金花,謝菊蘭.一種接收相干信號的盲多波束形成方法[J].雷達科學與技術,2015,13(6):567-571.DENG Jinhua,XIE Julan.A Blind Beamforming Method for Receiving Coherent Signals[J].Radar Science and Technology,2015,13(6):567-571.(in Chinese)

[2]婁寶芳,劉志國.一種高性價比的相控陣雷達新技術[J].雷達科學與技術,2015,13(3):245-248.LOU Baofang,LIU Zhiguo.A New Low-Lost Technology on Phased Array Radar[J].Radar Science and Technology,2015,13(3):245-248.(in Chinese)

[3]楊曉倩,劉海波,姜菡,等.基于數字陣列雷達的單脈沖測角技術研究[J].空軍預警學院學報,2013,27(3):184-187.

[4]YU K B.Digital Beamforming of Multiple Simultaneous Beams for Improved Target Search[C]∥IEEE Radar Conference,Pasadena,CA:IEEE,2009:1-5.

[5]YU K B,FERNANDEZ M F.Digital Beamforming of Sub-Aperture Cluster Beams with Enhanced Angle Estimation Capabilities[C]∥IEEE Radar Conference,Cincinnati,OH:IEEE,2014:239-244.

[6]李杰濤,陳國際,李偉,等.DBF同時多波束測角方法研究及工程實現[J].火控雷達技術,2013,42(2):19-22.

[7]張光義,趙玉潔.相控陣雷達技術[M].北京:電子工業出版社,2006:293-297.

An Approach for Simultaneous Multi-Beam Fitting Angle Measurement in Digital Array Radar at Subarray Level

LIU Yangtao,LI Xiaoming,CAO Shuhua
(AVIC Leihua Electronic Technology Research Institute,Wuxi214063,China)

Aiming at the application of digital simultaneous multi-beam technology in subarray-level digital array radar,a multi-beam fitting angle measurement method for subarray-level digital array radar is proposed.First,an approach to form simultaneous multiple beams by digital weighting is introduced.Then a fitting angle estimation model based on amplitude comparison method is established,and its implementation flow and steps are described.At last the simulation and analysis are carried on.The angle estimation precision is equal to that of digital monopulse angle estimation according to simulation results.And the angle estimation method can provide a wider range of angle measurement under the condition of keeping certain angle measuring accuracy.It is valuable for engineering application.

digital array radar;simultaneous multi-beam;fitting angle estimation;monopulse angle estimation;engineering applications

TN851;TN958

A

1672-2337(2017)02-0215-05

10.3969/j.issn.1672-2337.2017.02.018

2016-08-03;

2016-11-01

劉洋濤男,1984年出生,湖北京山人,碩士,工程師,主要研究方向為雷達系統、陣列信號處理。

E-mail:liuyangtao1015@163.com

李曉明男,1981年出生,河南漯河人,博士,高級工程師,主要研究方向為雷達系統、陣列信號處理。

曹書華男,1981年出生,安徽宿州人,碩士,高級工程師,主要研究方向為雷達系統。