基于廣義標簽多伯努利濾波的可分辨群目標跟蹤算法

朱書軍 劉偉峰,2 崔海龍

基于廣義標簽多伯努利濾波的可分辨群目標跟蹤算法

朱書軍1劉偉峰1,2崔海龍1

針對雜波條件下可分辨群目標的狀態估計、目標個數與子群個數估計問題,提出了一種基于標簽隨機有限集(Label random fi nite set,L-RFS)框架下的可分辨群目標跟蹤算法,該算法主要包括兩個方面:可分辨多群目標動態建模和多群目標的跟蹤估計.本文工作主要包括:1)結合圖論中的鄰接矩陣對可分辨群目標運動進行動態建模.2)利用基于L-RFS的廣義標簽多伯努利濾波(Generalizes label multi-Bernoulli,GLMB)算法對目標的狀態和個數進行估計,并且通過估計鄰接矩陣得到群的結構和個數估計.3)通過個數不同、結構不同的三個子群目標在二維平面分別做線性和非線性運動進行算法驗證.仿真分析表明本文算法能夠準確估計出群目標中各目標的狀態、個數以及子群的個數,并且能獲得目標的航跡估計.

可分辨群目標跟蹤,廣義標簽多伯努利濾波,鄰接矩陣,隨機有限集,圖論

在傳統的跟蹤系統中,由于被跟蹤目標距離雷達較遠并且雷達的分辨率不足,在雷達屏幕上被跟蹤目標顯示為一個點源信號,通常假設被跟蹤目標為一個點目標.所以,在傳統的多目標跟蹤算法中,假設被跟蹤目標最多產生一個量測,例如概率數據關聯(Probabilistic data association,PDA)算法[1]、聯合概率數據關聯(Joint probabilistic data association,JPDA)算法[2?3]、多假設跟蹤(Multiple hypothesis tracking,MHT)算法[4?5].群目標由多個相互協作的目標構成,并保持著一定的結構進行運動[6?7],如圖1所示.該群目標由三個子目標組成,當雷達距離該群目標較遠時,即使各子目標產生一個量測,該群目標也將產生多個量測,即能夠在一個整體的群目標中獲得多個量測.從單群目標角度來看,這使得基于一個目標至多產生一個量測假設的傳統跟蹤算法不再適用.另一方面,隨著現代傳感器技術的不斷發展,雷達的分辨率日益提升使得傳感器足以獲得實際目標大致輪廓.例如高分辨率雷達能夠從單個目標中獲得多個量測,通常稱這種目標為擴展目標,如圖2所示,通常從目標機翼、機首和機尾等容易反射雷達波的位置獲得多個量測.在動態建模、狀態估計和個數估計問題上,群目標和擴展目標都面臨著許多相似的科學問題:1)它們都具有一定的形狀,且都產生多個量測.2)量測之間的距離都小于跟蹤門的門限,使得傳統的數據關聯算法面臨挑戰.為了便于描述,本文將群目標和擴展目標統稱為群目標.

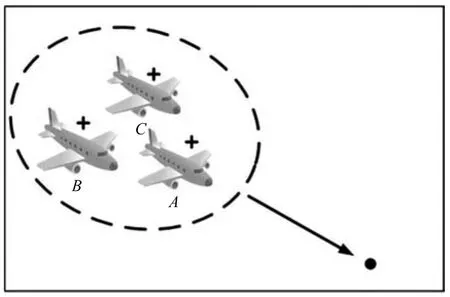
圖1 群目標(“+”表示量測)Fig.1 The group target(“+” denotes measurement)

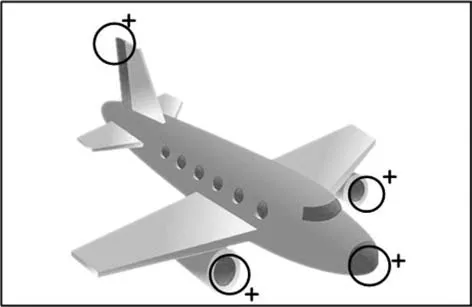
圖2 擴展目標(“+”表示量測)Fig.2 The extended target(“+” denotes measurement)

當群目標產生的量測位于傳感器同一個分辨單元內時,我們認為該群目標不可分辨,稱為不可分辨群目標.在文獻[8]中,Koch引進了不可分辨擴展目標的概念并且結合隨機矩陣理論[9?10]提出了基于經典貝葉斯框架下的擴展目標跟蹤算法,該算法將基于傳統的卡爾曼濾波單點源目標跟蹤算法擴展到單個擴展目標跟蹤.使用該算法可以得到擴展目標的形心點,同時通過估計二階矩獲得擴展目標的近似橢圓形狀.該方法在無雜波環境下跟蹤單個擴展目標.

在文獻[11]中,提出了基于貝葉斯框架的多群目標跟蹤算法,該算法以群目標的整體運動趨勢為跟蹤對象,通過建立群目標的中心和觀測量之間的相互作用約束模型來估計目標數目和目標運動狀態,該方法不能形成目標航跡并且無結構估計問題.在文獻[12]中,提出了基于箱式粒子濾波的群目標跟蹤算法,該算法基于廣義似然函數加權的粒子濾波算法,即在原有的粒子濾波算法的基礎上,利用廣義似然函數的積分解來計算區間量測下的粒子權重,從而獲得群目標的狀態估計,該算法屬于點集估計,不能獲得群目標中各目標的運動軌跡.在文獻[13]中,Baum等引進了隨機超面模型,通過假設每個量測源是隨機生成的超曲面中的一個元素,從而對擴展目標進行跟蹤估計.在文獻[7]中,針對多個固定個數的擴展目標問題,提出了采用隨機采樣的方法進行擴展目標的狀態估計.

隨機有限集理論為解決群目標跟蹤問題提供了另一種解決思路.在文獻[14?15]中,Gilholm和Salmond首次提出了基于泊松分布的擴展目標模型.Mahler提出了擴展目標概率假設密度(Extended target probability density,ET-PHD)[16],該方法可以同時獲得目標狀態估計和個數估計,并且該方法不需要考慮數據關聯.在文獻[17?18]中,Granstr¨om 等提出了高斯混合擴展目標跟蹤(Gaussian mixture extended target PHD,GMET-PHD)算法.在文獻[19]中,Orguner等提出了針對擴展目標的勢概率假設密度(Extended target cardinality PHD,ET-CPHD).在文獻[20]中,提出了一種針對群目標的跟蹤算法,該算法基于序列蒙特卡洛概率假設密度濾波器(Sequential Monte Carlo probability hypothesis density fi lter,SMC-PHDF),并用高斯混合模型(Gaussian mixture models,GMM)擬合SMC-PHDF中經重采樣后的粒子分布,通過估計混合模型的參數獲得質心狀態、形狀和群個數估計.在文獻[21]中,將基于勢平衡多伯努利濾波(Cardinality balanced multitarget multi-Bernoulli,CBMeMBer)算法推廣到擴展目標跟蹤算法,并且給出了高斯混合條件下的算法.文獻[22]使用圖論結合蒙特卡洛方法估計出群目標的狀態,但是該方法局限于目標個數是固定的情況.在文獻[23]中,Ristic等提出了針對擴展目標的伯努利濾波算法(Extended target Bernoulli fi lter,ET-BF),用于跟蹤單個擴展目標.在文獻[24?25]中提出了廣義標簽多伯努利濾波(GLMB)多目標跟蹤算法,GLMB濾波器不僅擁有CPHD和PHD濾波器的優點,并且GLMB濾波算法能夠通過給各目標添加一個獨有的標簽來獲得各目標的軌跡估計.文獻[26]將GLMB多目標濾波算法擴展到多擴展目標跟蹤算法,但該算法只針對擴展目標,不涉及群結構估計問題.

傳統群目標估計算法一般假設目標個數固定且不受雜波干擾.基于隨機有限集(Random fi nite set,RFS)的估計算法可以有效解決上述問題,并且能夠有效避免數據關聯分配過程.從這個角度來講,RFS更適合于解決群目標的跟蹤問題.為了得到各目標的軌跡估計,本文在標簽RFS(Label RFS,L-RFS)框架下,采用GLMB濾波算法.由于現有的群目標跟蹤算法中,都不涉及可分辨群目標的結構估計問題.因此,本文擬通過引進圖理論來描述該群目標的結構.

可分辨群目標產生的多個量測位于傳感器不同的分辨單元中.相對于不可分辨群目標(或部分可分辨群目標),可分辨群目標運動不僅存在協作關系,并且目標之間的結構關系需要估計.隨著高分辨率雷達的廣泛使用,針對可分辨群目標的跟蹤估計也越來越重要.在此,本文采用了圖理論結合GLMB濾波算法對可分辨群目標進行跟蹤.首先,借助圖理論對可分辨群目標運動狀態建模.在此基礎上,再對可分辨群目標跟蹤估計.具體而言:1)由于起始階段群目標之間的協作關系未知,因此假設群目標之間是獨立的并采用GLMB濾波算法獲得各目標的狀態估計和軌跡估計以及目標的個數估計.2)在獲得群目標中各成員的狀態估計基礎上,通過計算每時刻的偏差矩陣估計獲得鄰接矩陣估計,并通過鄰接矩陣得到群的結構關系.再利用圖理論中連通圖的概念估計子群個數.

本文是文獻[27]的后續研究工作.文獻[27]只給出了群目標的動態建模方法以及獲得群目標中各成員的狀態估計方法.本文在文獻[27]的基礎上,對群目標鄰接矩陣估計方法進行了分析說明,從而能夠獲得群目標的結構信息,并且本文給出了非線性可分辨群目標估計的方法.實驗結果較文獻[27]更為全面.

本文使用的定義和一些數學符號約定如下:〈f,g〉=?f(x)g(x)dx表示f和g的內積.[h(·)]X=∏x∈Xh(x)為多目標的冪形式,按照約定,當X=?時,該式等于1,并且X 可以為向量或集合.多目標環境下的Kronecker delta函數和指示函數如下所示

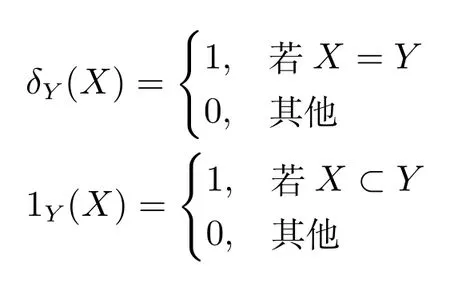
其中,X和Y表示集合.為了便于區分,XXX和X分別表示帶標簽集合和不帶標簽集合,xxx和x分別表示帶標簽向量和不帶標簽向量,X和L分別表示狀態空間和離散標簽空間.{(x1,l1),···,(xn,ln)}∈X×L表示標簽隨機有限集XXX.GLMB濾波算法要求不同目標的標簽是不同的,因此,用下述表達式作為約束

其中,L(X)={L( x): x ∈X},L(x)=L((x,?))=?.

1 背景

1.1 隨機有限集(RFS)

多目標環境下,在k時刻,目標的個數和狀態可以用以下RFS表示[28]:

Xk不僅描述了目標的狀態改變信息,還包括目標消失、新目標出生等目標個數變化情況.因此,有限隨機變量Xk包含了多目標的所有動態信息.同理,可以建立如下觀測RFS[25]:

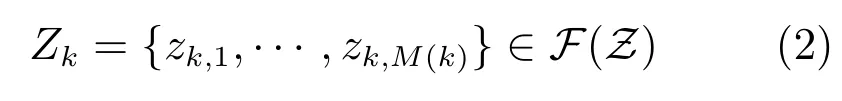
RFS Zk包含了雜波、目標觀測以及漏檢信息.在式(1)和式(2)中,N(k)和M(k)分別表示k時刻目標和量測個數,X?Rnx和Z?Rnz為目標狀態空間和觀測空間,F(X)和F(Z)分別為X和Z的所有有限子集構成的集合.在k時刻,一些目標會繼續存活并且狀態改變,一些目標可能會再生出(Spawned)新目標,新目標出生,一些目標可能消亡,因此,可建立如下RFS狀態模型:

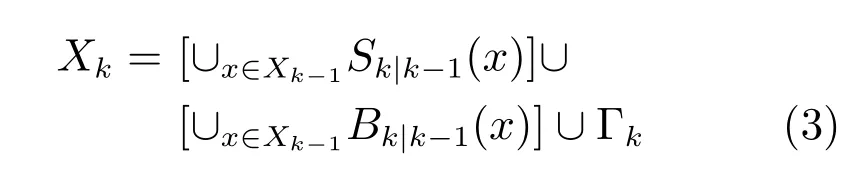
其中,Sk|k?1(x),Bk|k?1(x)和Γk分別表示目標的存活、再生和新生RFS.

多目標狀態RFS從k?1時刻到k時刻的變化可通過RFS轉移概率密度函數描述[29]

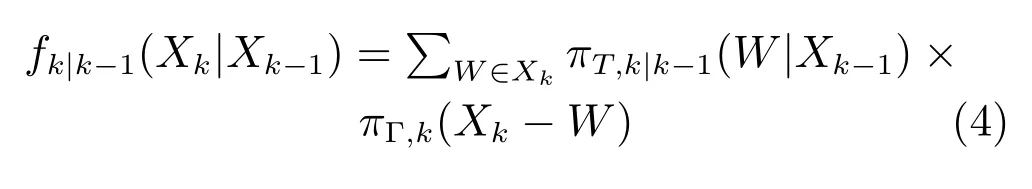
其中,πT,k|k?1(·|·)表示存活 RFS Tk|k?1的置信概率密度,πΓ,k(·)表示新生目標的置信概率密度.

1.2 伯努利分布

單伯努利RFSX描述單個目標狀態集,其概率密度如下

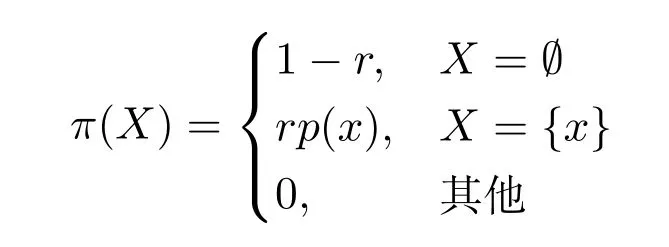
其中,r表示單個目標x的存在的概率,p(x)為目標x概率密度.

多伯努利RFSX可看作為固定個數且相互獨立的單伯努利RFSX(i)的聯合即各單伯努利存在概率為r(i),概率密度為p(i),對于有n個成員的隨機有限集{x1,···,xn},其多伯努利概率密度函數表示如下[26]

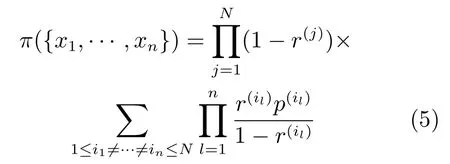
1.3 標簽RFS

與傳統的RFS不同,標簽RFS在目標狀態x∈X添加了標簽?∈L={αi:i∈N}變量,其中N表示目標的個數.標簽多伯努利密度函數如下[22]

其標簽多伯努利密度的簡化描述形式為

2 問題描述

與一般的多目標問題不同,可分辨群目標中多個目標以一定的協作模式運動,各目標按照一定的圖結構模式協作運動.為描述可分辨群目標的結構,本文引進圖理論描述群目標中各節點(目標)間相互關系.該方法已經在飛行器編隊控制和多代理控制方面得到了成功的應用[30?31].

2.1 鄰接矩陣

定義1.圖是由兩個集合Ve和Ed組成,記為G=(Ve,Ed),其中Ve表示節點的非空有限集合,Ed表示邊的有限集合,當這些邊有方向時則稱為有向圖,無方向時稱為無向圖.

借助圖結構和群結構的相似性,本文引進了鄰接矩陣來描述可分辨群目標結構.鄰接矩陣能夠描述群中目標之間的協作關系,本文使用非對稱的鄰接矩陣,即鄰接矩陣描述相互聯系目標的父子關系.目標鄰接矩陣其中,當第i個目標是第j個目標父節點時,a(i,j)=1.其他情況,a(i,j)=0.例如,3個目標構成的群關系如圖3所示.則該群的鄰接矩陣如下

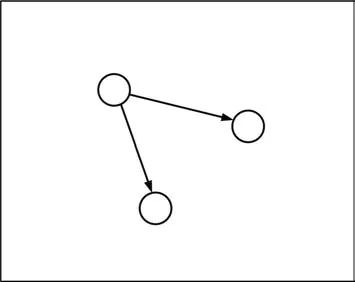
圖3 群目標結構模型Fig.3 The structure model of group target

2.2 系統模型

若每目標存在單個父節點時,可分辨群目標運動模型如下

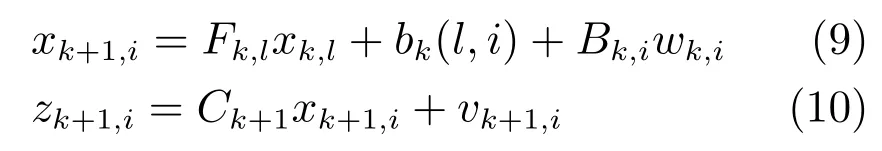
根據鄰接矩陣可以判斷出群中各目標之間的連接及父子關系,如果某個目標沒有父親節點,則該目標被稱作頭節點,頭節點的運動會影響到其子目標,而頭節點自身運動不受其他目標影響.因此,頭節點運動模型中補償向量bk(l,i)=0,并且xk,l為它自身在k時刻的狀態.否則,該目標存在著父節點并且該目標的運動受其父節點影響,因此該目標運動模型中補償向量bk(l,i)包含該節點與其父節點之間的方向和距離信息,當目標存在多個父節點時,線性條件下xk+1,i表示如下其中,P(i)表示目標i的所有父節點.

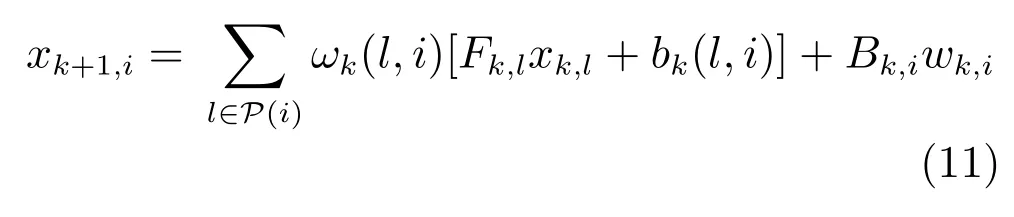
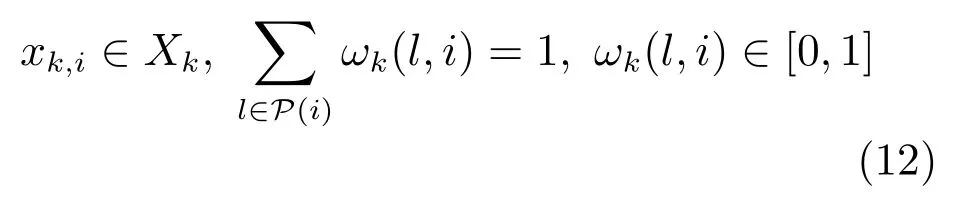
例如,群目標結構模型如圖3所示,目標1是頭節點,目標2和目標3是目標1的子節點,那么群目標的運動模型如下假設權重ωk?1(l,i)為等權重,建立群目標運動模型的主要步驟如下:

步驟1.遍歷群中所有1～n個節點.

步驟2.通過鄰接矩陣找到該節點的父節點.

步驟3.如果該節點存在父節點

步驟4.如果該節點不存在父節點

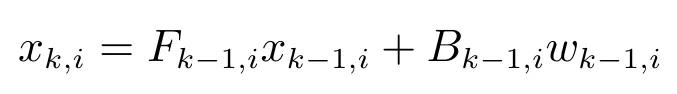
3 可分辨群目標估計

δ-GLMB[24]濾波可以同時獲得群中各成員的狀態估計.在獲得各成員的狀態估計的基礎上,再估計每時刻鄰接矩陣獲得可分辨群目標的結構關系,并通過鄰接矩陣得到子群個數估計和群狀態估計.

3.1 群成員估計

由于群內各成員之間的距離相對一般的多目標比較接近,采用的基于RFS的濾波算法更適合群目標跟蹤.為了獲得各目標的軌跡估計,選擇GLMB濾波算法對群目標進行跟蹤估計.群目標之間協作運動,目標之間的狀態并不獨立,由于起始階段的群目標之間的協作關系未知,群結構和狀態相互耦合.因此,我們采用一種兩階段的算法,在第一階段,把群目標看作為獨立運動.使用GLMB濾波算法估計目標的狀態和個數.標準GLMB的算法定義如下[24?25]:

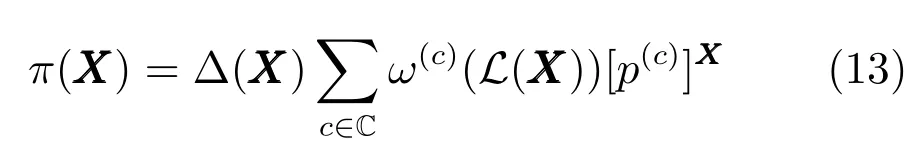
其中,C表示離散變量,p(c)(·,?)表示目標?的概率密度,設ω(c)(I)為權重并且滿足=1,F(L)為L上所有有限子集的集合.該標準GLMB濾波算法在貝葉斯遞推下封閉[19].

為了便于計算,將式(13)變形為

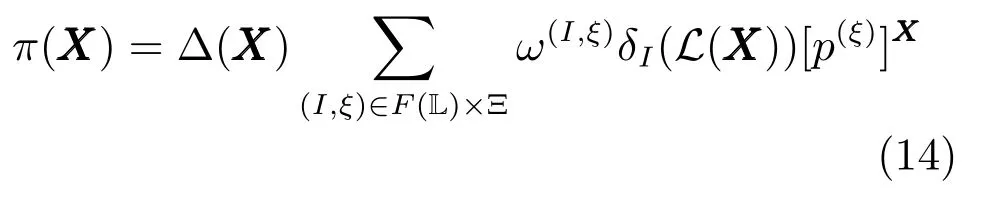
式(14)稱為δ-GLMB.

例如,在k時刻,其中Ξ為空集,假設有以下兩種可能

1)有0.2的概率存在1個目標,標簽為(0,2),即在k時刻存在目標(0,2)(即0時刻產生的目標2),并且該目標的概率密度為p(·,(0,2))=N(·;m,P2).

2)有0.8的概率存在2個目標,標簽分別為(1,1)和(0,2)(即1時刻產生的目標1,0時刻產生的目標2),概率密度分別為p(·,(1,1))=N(·;0,P1)和p(·,(0,2))=N(·;m,P2).

0時刻的δ-GLMB表達式為

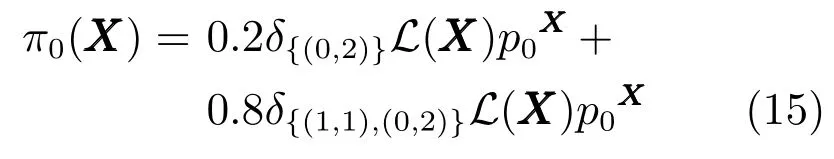
預測步.當多目標的先驗概率密度形式如式(14)所示時,δ-GLMB的預測步為

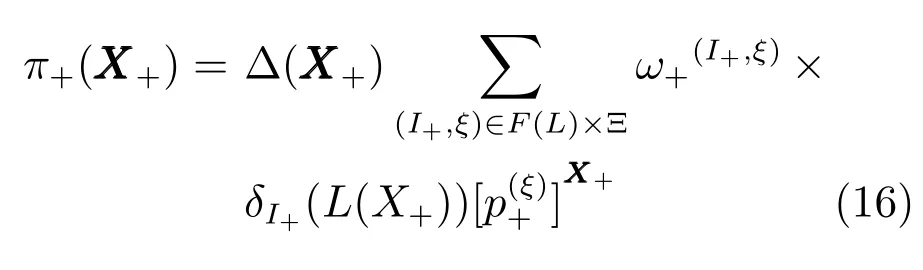
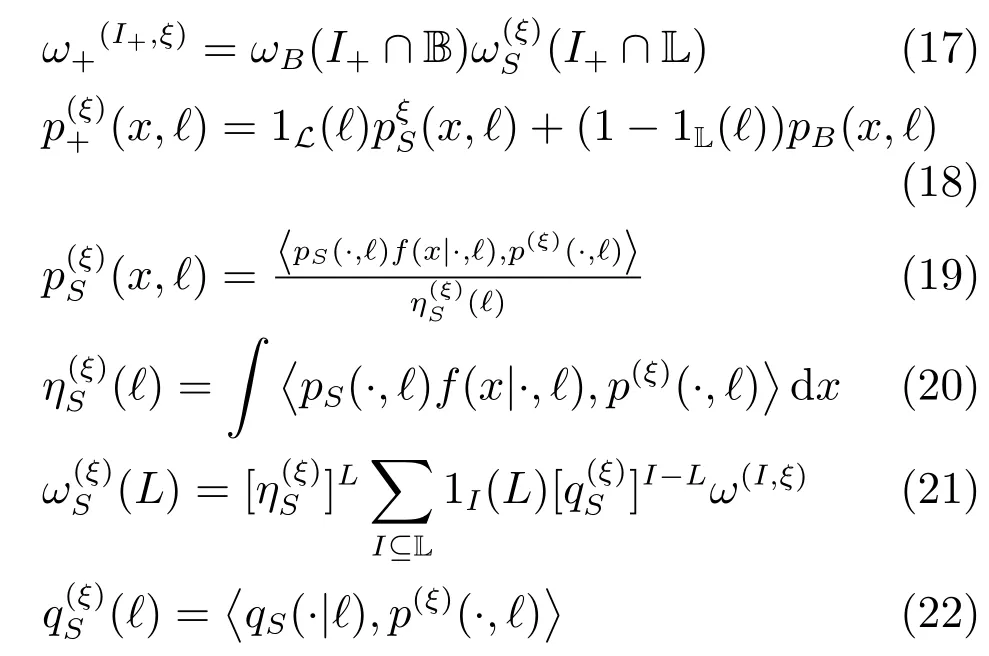
其中其中,ωB(I+∩B)是新生標簽I+∩B的權重,是存活標簽(I+∩L)的權重.pB(·,?)是新生目標的概率密度,p(Sξ)(x,?)是由先驗密度p(ξ)(·,?) 得到的存活目標的密度.f(·|·,?) 表示存活目標的概率密度.

更新步.如果多目標的預測密度如式(14)所示時,則更新步為

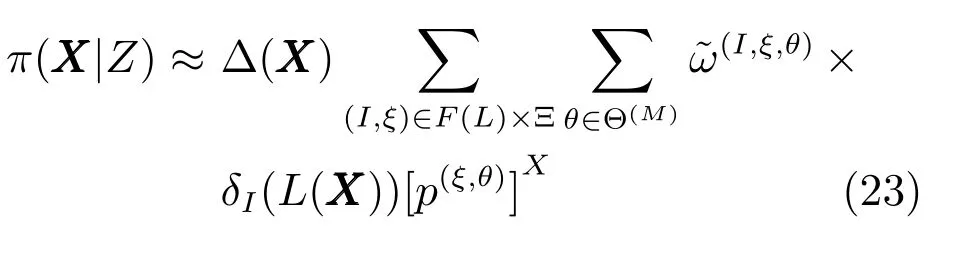
其中,在一個固定的 (I,ξ) 中,Θ(M)={ξ(1),···,ξ(M)}集合表示在最大權重ω(I,ξ,θ(i))時的 Θ 的M個元素.為截斷后的歸一化權重.

3.2 鄰接矩陣和群個數估計

在獲得可分辨群目標中各成員狀態估計的基礎上,通過各時刻鄰接矩陣估計來得到各群目標的結構信息.

1)偏差矩陣估計:通過GLMB濾波算法獲得各個目標的狀態估計,表示在k時刻的群目標的狀態估計集.為了得到k時刻群的結構,首先估計k時刻的鄰接矩陣,由于鄰接矩陣不能直接得到,引入了偏差矩陣表示各目標之間狀態的差值.使用目標的狀態估計獲得偏差矩陣估計

其中,dk(i,j)定義如下向量2范數

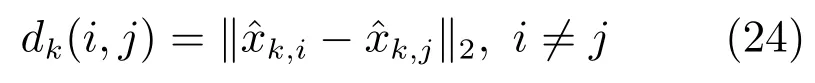
通過式(11)中的偏差向量bk(l,i)和偏差矩陣以估計鄰接矩陣.本文通過以下方法得到每時刻的鄰接矩陣估計.

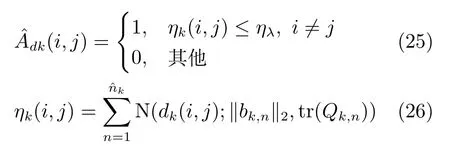
其中,ηλ表示ηk(i,j)的閾值,當ηk(i,j)小于該閾值時,?Adk(i,j)等于1,反之為0.Qk,n為過程噪聲的協方差陣.

這樣可以得到每時刻可分辨群目標的鄰接矩陣估計.由dk(i,j)定義可知dk(i,j)=dk(j,i),因此偏差矩陣估計是一個對稱矩陣.而鄰接矩陣估計由偏差矩陣估計得到,因此鄰接矩陣估計也是對稱的.由對稱的鄰接矩陣得到的是無向圖,無向圖可以獲得圖中各節點的相互聯系信息卻不能獲得節點之間的父子關系.為了得到相互聯系目標之間的身份,我們做出以下假定:兩個協作運動的目標,在前方的目標為父節點.這種規定是符合現實中的真實情況的(父節點往往運動在子節點的前面).例如,假設兩個運動中的群如圖4所示.

在圖4的兩組群目標中,群1向上運動,目標A在目標B的前方,因此,目標A是目標B的父節點.群2向下運動,且目標C在目標D的前方,因此,目標C是目標D的父節點.

由集合的性質可知集合中的元素沒有順序之分.因此,在同一時刻針對同一個群,通過群的的狀態估計集合得到的鄰接矩陣估計并不是固定的.為了判斷兩個不同的鄰接矩陣是否描述同一個群,本文引入了同構的概念[32].

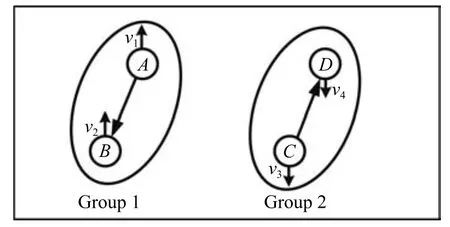
圖4 目標之間依賴關系Fig.4 The dependencies of targets

定義2.G1=(Ve1,Ed1)和G2=(Ve2,Ed2)分別表示兩個圖.如果存在一個雙射函數?:Ve1→Ve2,并且針對所有的節點vei,vej∈Ve1有veivej∈Ed1??(vei)?(vej)∈Ed2,那么,稱G1和G2同構,并記G1?G2,因此,如果兩個鄰接矩陣是同構的,則它們是相互等價的.

2)子群個數估計:實際上,子群的個數估計等價于對群進行劃分.圖5給出了群目標示例,圖中總共11個目標構成了三個子群目標.目標狀態集合的元素次序是不相關的,因此相應的鄰接矩陣也會隨著時間變化.從圖5可知,每個子群被視作一個連通圖,即群中任意兩點是連通的,但整個群并不是一個連通圖,因為子群1、子群2和子群3之間沒有相互聯系,稱這些多個連通圖組成的非連通圖為森林.受此啟發,采用連通圖的概念去估計子群的個數.因此,首先定義了如下的Laplacian矩陣

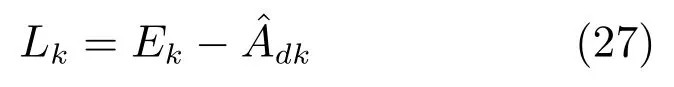
其中,Ek是對稱矩陣并且等于diag{ek,1,···,ek,nk},其中ek,i表示圖中頂點vk,i的自由度即連接到該頂點的邊數.?Adk是鄰接矩陣估計.子群的個數等價于森林中連通圖的個數,即可用下述引理表示[33].

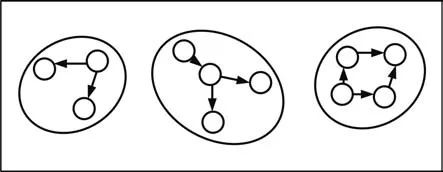
圖5 三個群目標結構Fig.5 Three group targets structure

引理1.在Laplacian矩陣的特征值中,0出現的次數即為連通圖的個數,即群目標中子群個數.

3.3 非線性可分辨群目標估計

針對非線性目標系統,給出如下群目標的動態模型

其中,假設補償向量是加性的.對比式(11)和式(28)可以發現非線性系統和線性系統是類似的,其中補償向量bk(l,i)也包含子目標與父目標之間的偏差.與線性系統不同的是目標的狀態方程屬于非線性函數.同樣,假設各目標之間是相互獨立的,采用UKF-GLMB濾波器來估計出各目標的狀態.最后使用與線性系統下相同的方法估計出群的結構與子群個數.其中,UKF-GLMB算法如下:

算法1.UKF算法

步驟1.構造目標n初始sigma點

1)噪聲擴維初始狀態點

2)構造2ns+1個擴維Sigma狀態點

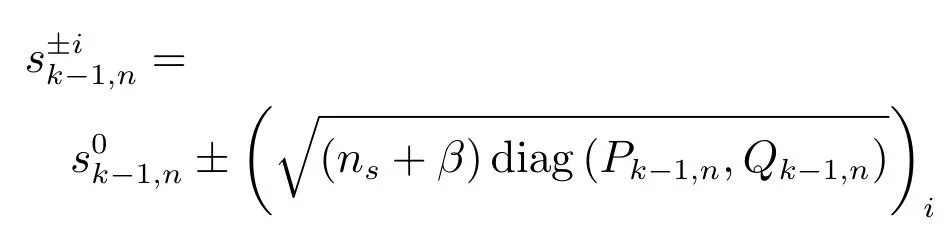
3)Sigma狀態點權重

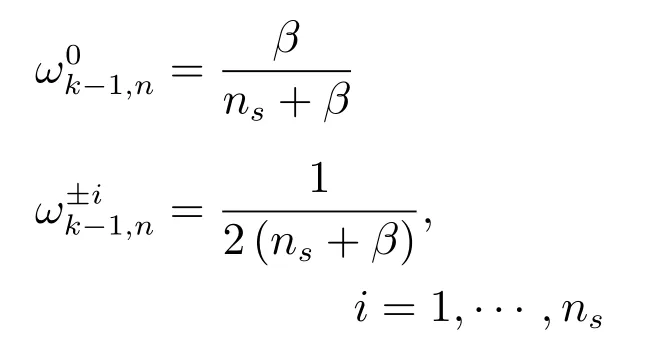
步驟2.預測步

1)預測一階矩:Sigma點狀態預測及目標狀態預測點

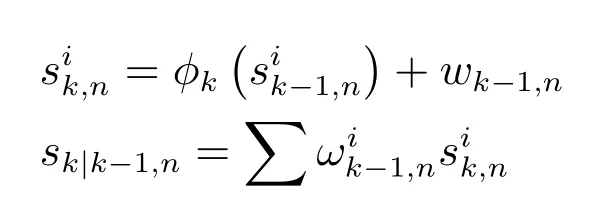
2)預測二階矩:目標狀態協方差陣

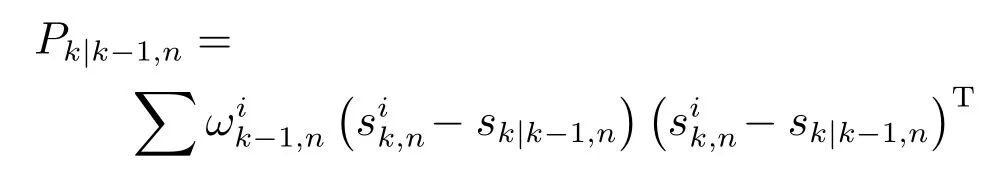
步驟 3.狀態–量測互協方差陣Sk,n及增益Kk,n計算

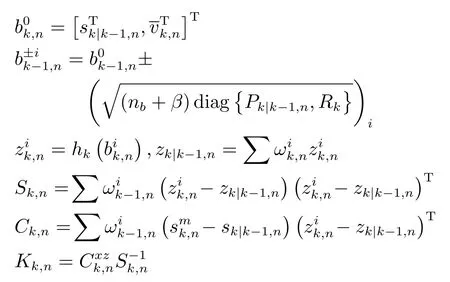
步驟4.更新步

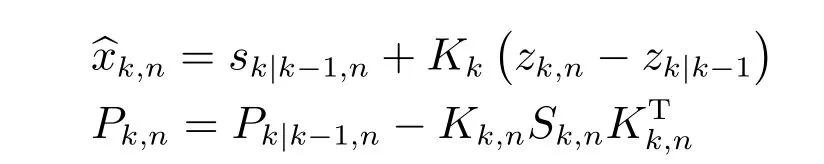
算法 2.UKF- δ-GLMB 算法

步驟1.給定初始Sigma點:

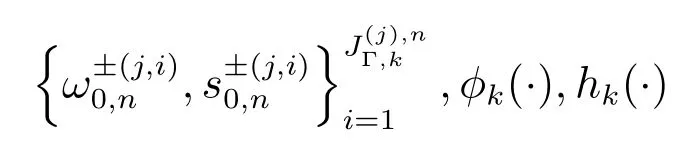
步驟2.Sigma 點參數預測:

步驟 3.Sigma點參數更新:獲取目標狀態協方差矩陣目標存在概率rk.n,見算法1.

步驟4.獲得群結構與狀態估計:

1)獲得偏差估計矩陣,式(24);

2)估計鄰接矩陣,式(25).

4 仿真實現

本節分別考慮線性和非線性系統兩個實驗來驗證本文所給算法.在實驗1中使用GLMB和CBMeMBer[34]進行比較,在實驗2中使用UKFGLMB和UKF-CBMeMBer算法進行比較.

4.1 實驗1:線性系統

本仿真實驗的群目標如圖5所示,包含3個子群目標,子群在2維平面中做勻速直線運動.運動場景大小為 [?2000,2000]×[?2000,2000]m2,仿真時間為100s.3個子群分別在不同的時間和地點出生和消失.子群1的頭節點在時刻k=20s時出生在 [?1800m,20m/s,?1900m,20m/s],方便起見,假設群1中的各目標同時在k=80s時消失.子群2的頭節點在時刻k=30s時出生在[1800m,?20m/s,?1800m,30m/s], 假設子群 2中的各目標同時在k=95s時消失.子群3的頭節點在時刻k=0s時出生在[1800m,?10m/s,1800m,?10m/s],假設子群3中的各目標同時在k=100s時消失.觀測噪聲和過程噪聲的協方差陣分別為Rk,i=diag{100,100}m2,Qk,i=diag{4,4}m2,i=1,2,···,11. 為集中考慮群結構估計問題,假設檢測概率Pd=1,目標的存活概率為Ps=1.分別采用GLMB濾波和CBMeMBer濾波器對該多群目標進行跟蹤估計.

在整個跟蹤過程中,假設這三個子群目標是相互獨立的,并且總目標的個數和子群的個數是未知的.多群目標的真實運動軌跡如圖6所示,其中不同的曲線代表不同目標的運動軌跡,三角形表示目標終點,圓形表示起點.

圖6 多群目標真實軌跡Fig.6 The true tracks of groups

由CBMeMBer濾波算法和GLMB濾波算法得到的軌跡估計分別如圖7和圖8所示.由GLMB濾波算法得到的狀態估計如圖9所示.為評估本文所給算法的性能,采用最優子模式分配距離(Optimal sub pattern assignment,OSPA)[35]

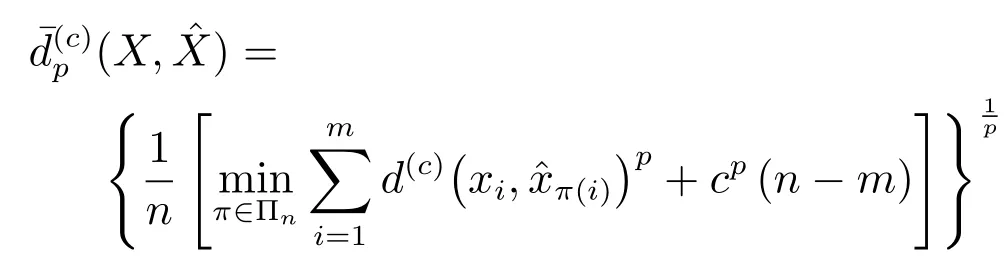
其中,X和分別為目標真實狀態集和估計狀態集,個數分別為m和n,且m≤n,1＜p＜∞,c＞0,Πk表示1,2,···,k所有各種排列組成的集合.圖10給出了經50次蒙特卡洛(Monte Carlo,MC)仿真后得到的OSPA結果.

各時刻目標真實個數和估計個數如圖11所示.每時刻的子群真實個數和子群個數估計如圖12所示.

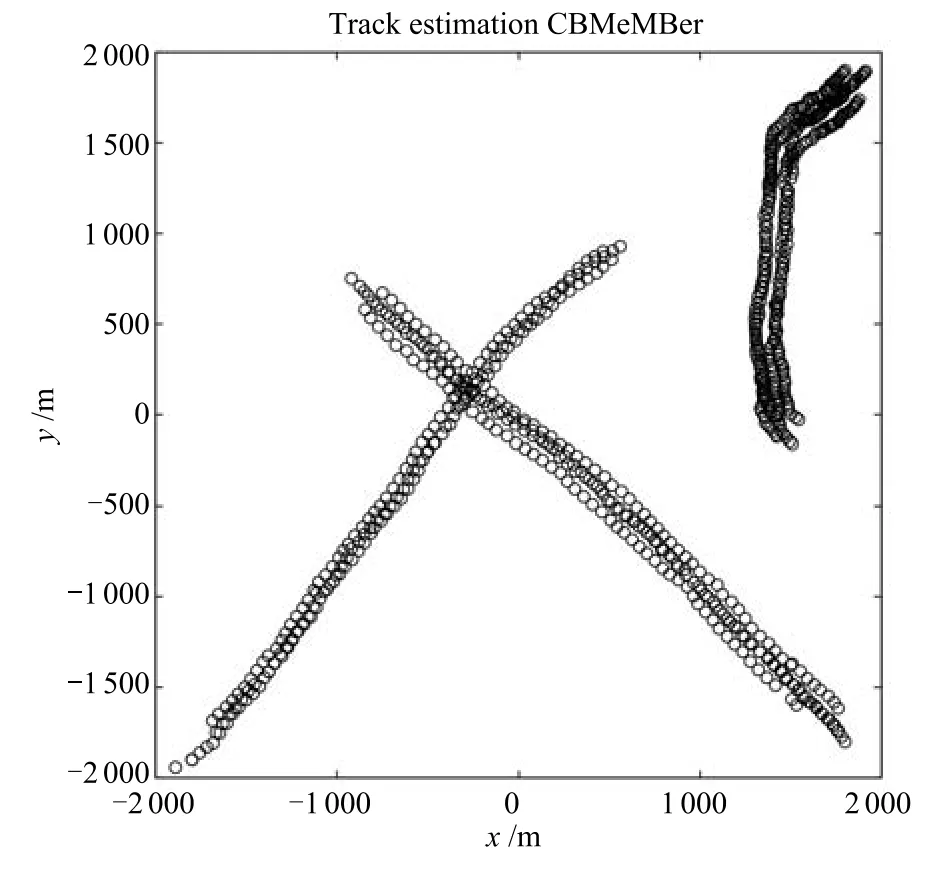
圖7 由CBMeMBer濾波器得到的軌跡估計Fig.7 Track estimation by CBMeMBer fi lter

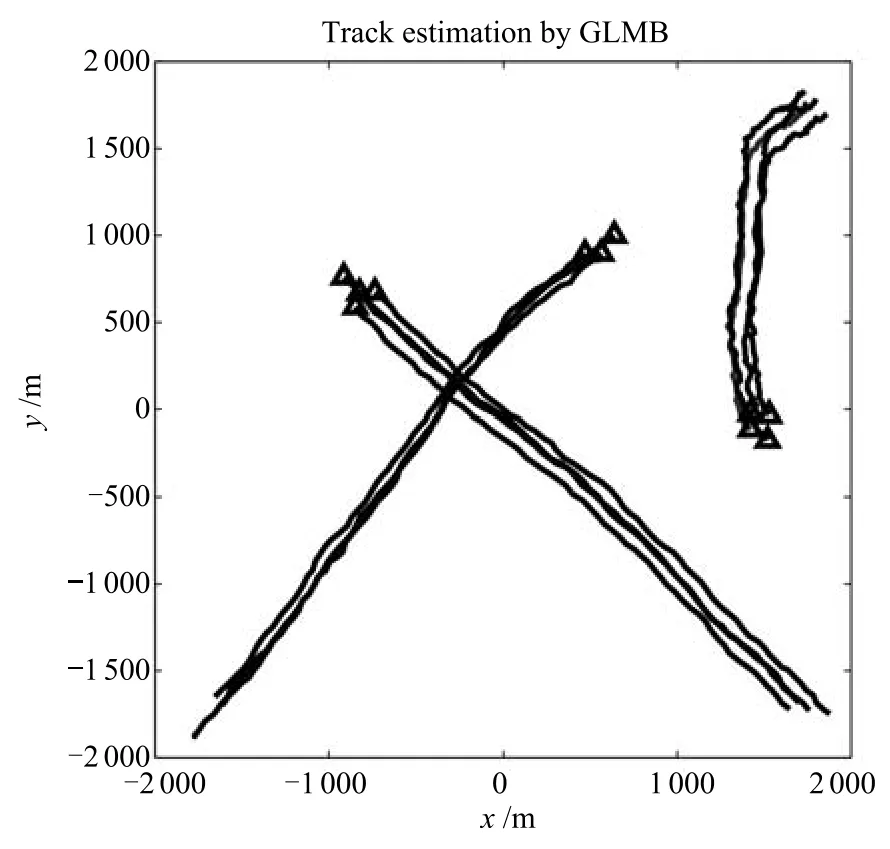
圖8 由GLMB濾波器得到的軌跡估計Fig.8 Track estimation by GLMB fi lter

由于GLMB濾波算法為每個目標添加了不同的標簽,因此在算法的實現中能夠辨別每個目標的身份標簽.可以得到如圖8所示的各個目標的軌跡估計,而CBMeMBer濾波算法獲得點集航跡,如圖7所示,目標的運動軌跡由獨立的圓圈組成,因此不能獲得目標航跡.

在圖9中,估計點和真實軌跡基本吻合,GLMB濾波算法能夠準確估計出各目標的運動狀態,從圖10的OSPA Loc圖中可以知道CBMeMBer濾波算法也能很好地估計出各目標的運動狀態.

從圖10和圖11中的OSPA Card可知,當真實目標個數發生變化時,GLMB濾波算法對目標的個數估計出現了一個延遲過程.例如,在第15s,目標個數發生變化,GLMB濾波算法經歷6s后跟上目標個數變化,而CBMeMBer濾波算法只需經歷1s后并能跟上目標個數變化,然而在這過程后,GLMB濾波算法能夠較穩定地估計出目標個數,而CBMeMBer濾波算法在目標個數的估計過程中出現較多的波動.

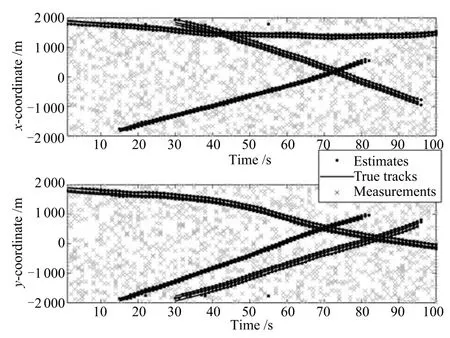
圖9 由GLMB濾波算法得到狀態估計Fig.9 The state estimation by GLMB fi lter

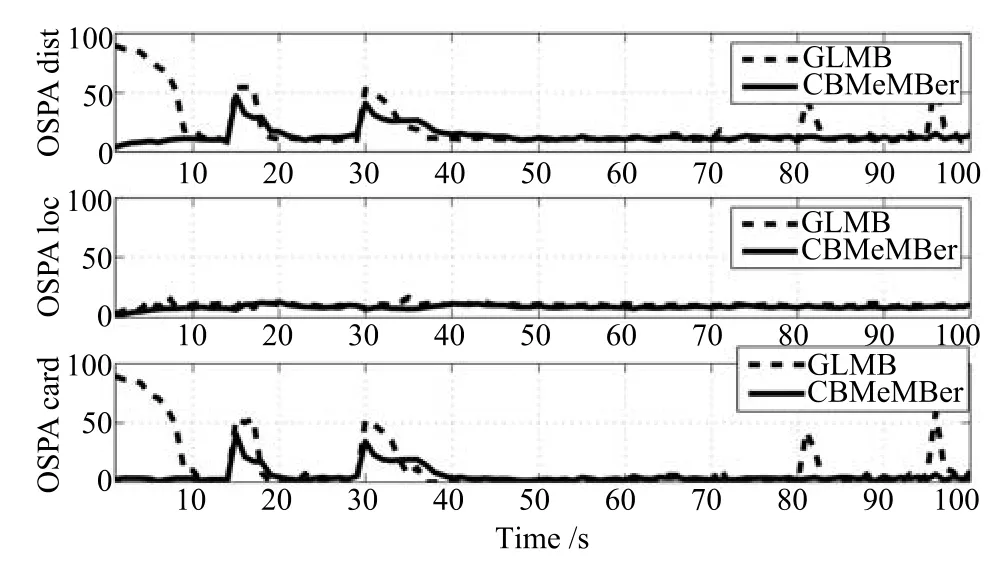
圖10 OSPA距離對比圖（經50次MC平均）Fig.10 50 MC run average of the compare of OSPA

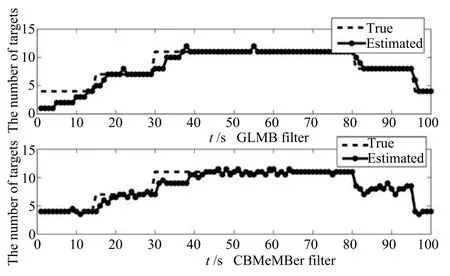
圖11 目標個數估計Fig.11 The estimated number of targets

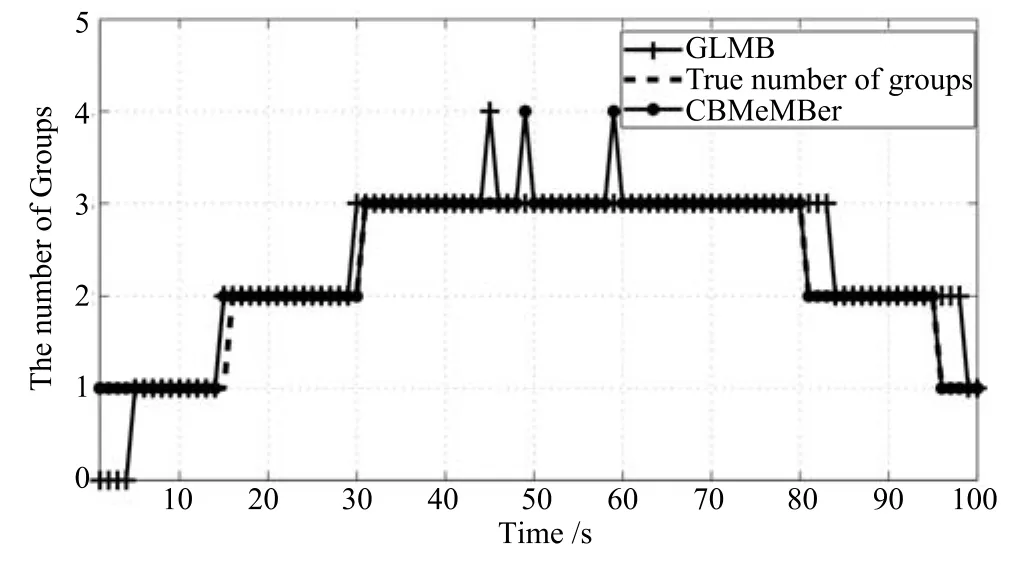
圖12 子群個數估計Fig.12 The estimated number of groups

由圖12可以知道,GLMB濾波算法和CBMeMBer濾波算法都能夠很好地估計出每時刻群的個數.

4.2 實驗2:非線性系統

在本仿真實驗中,子群的個數以及各子群的結構和出生時間、地點以及消失時間和實驗1一致.各群的運動軌跡如圖13所示,保持轉速未知的勻轉彎(CT)運動.各子群目標的父節點的動態模型如下

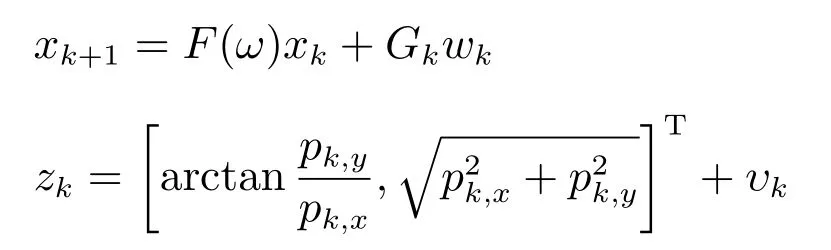
其中,F(ω)和Gk的定義如下

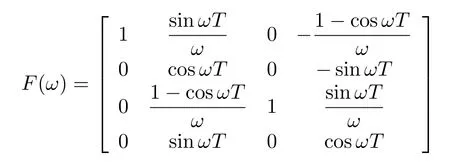
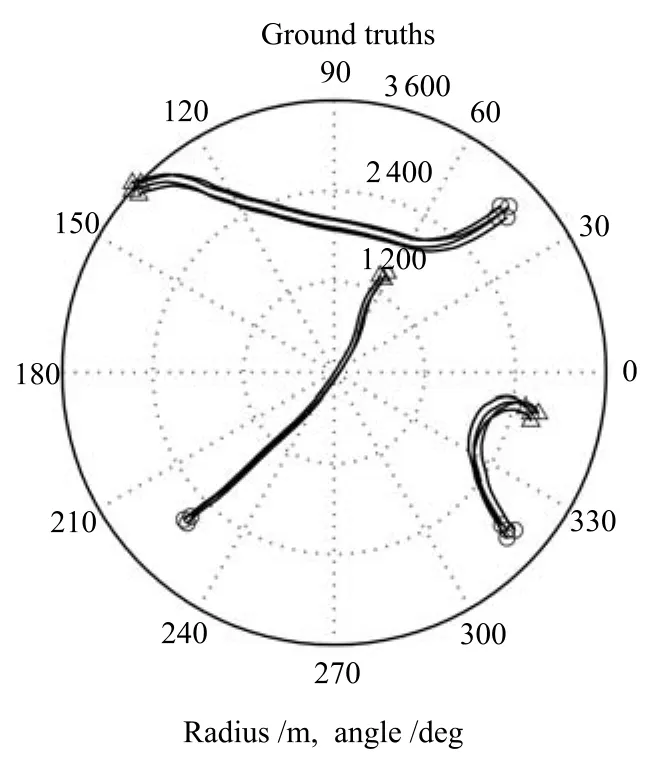
圖13 多群目標真實軌跡Fig.13 The true tracks of groups

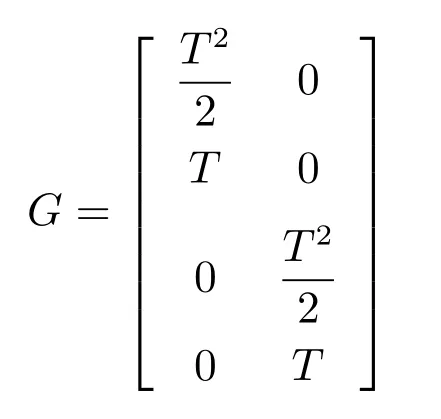
由UKF-GLMB濾波算法得到的狀態估計如圖14所示,目標個數估計如圖15所示,OSPA距離如圖16所示,子群個數估計如圖17所示.

由圖14可知,UKF-GLMB濾波算法在非線性系統下也能夠準確估計出各時刻各目標的運動狀態,由圖16中的OSPA Loc可知UKF-CBMeMBer濾波算法對目標的狀態估計效果較差.由圖15可知,在非線性系統下,UKF-GLMB濾波算法和UKFCBMeMBer濾波算法的目標個數估計效果和在線性系統下的估計效果差不多:UKF-GLMB濾波算法在估計過程中有延遲時間,UKF-CBMeMBer濾波算法在估計的過程中出現較大的波動.

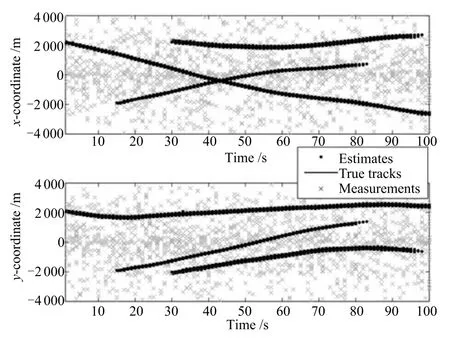
圖14 由GLMB濾波算法得到的狀態估計Fig.14 The state estimation by GLMB fi lter

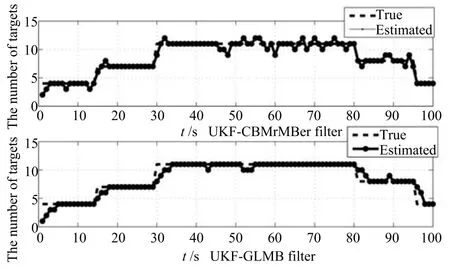
圖15 目標個數估計Fig.15 The estimated number of targets

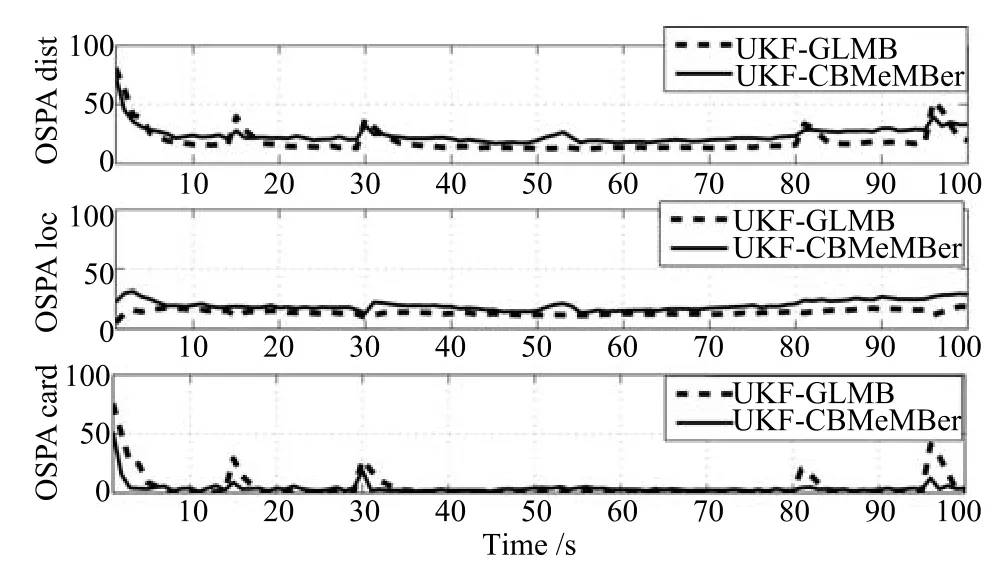
圖16OSPA距離對比（經50次MC平均）Fig.16 The OSPA distance(50 MCs)

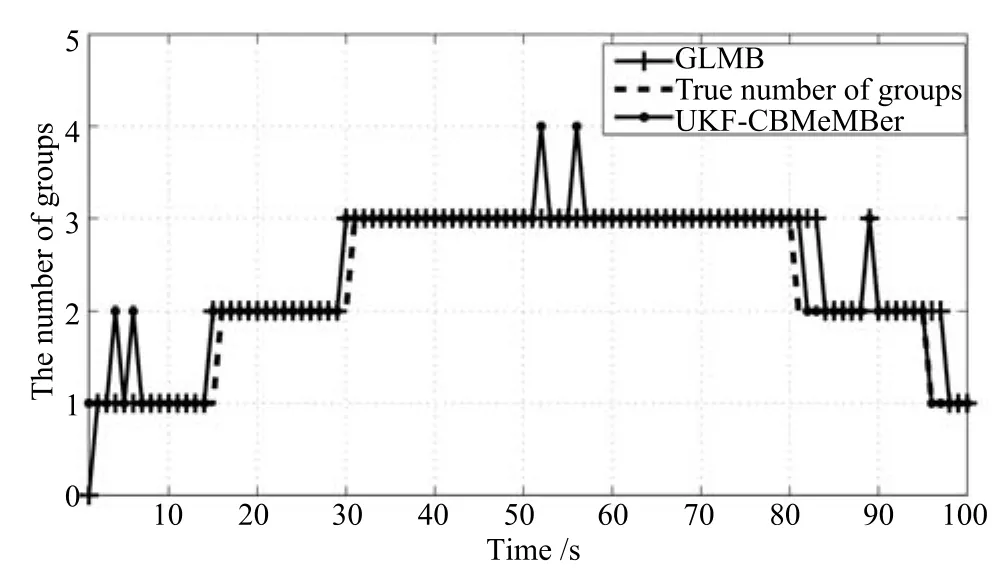
圖17 群的個數估計Fig.17 The estimated number of groups

由圖17可知,在非線性系統下,UKF-GLMB濾波算法和UKF-CBMeMBer濾波算法都能夠很好地估計出子群的個數.

4.3 算法性能分析

本文采用平均每步所消耗的CPU時間對GLMB濾波算法和CBMeMBer濾波算法進行性能分析.針對上述仿真,平均每步實驗所消耗的CPU時間如表1所示,用于測試算法的PC機的CPU為Intel(R)Core(TM)i5-4460M 3.20GHz,RAM為4GB,32位Win7系統.

表1 算法性能分析Table 1 Performance analysis of algorithms

從表1可以發現,GLMB算法和CBMeM-Ber算法在非線性系統下所消耗的時間都要大于線性系統下消耗的時間.并且由于標簽變量需要預測和更新,目標狀態分布項數增加,使得計算量增加,導致GLMB算法消耗的時間大于CBMeMBer算法消耗的時間.但是使用GLMB濾波算法,在跟蹤的過程中可以獲得群中各目標的身份.

5 結論

本文針對在雜波環境下子群個數和目標個數位未知的可分辨群目標跟蹤問題,提出了一種基于GLMB濾波算法的可分辨群目標跟蹤算法.1)根據群結構的先驗信息獲得各子群的鄰接關系矩陣信息;2)借助鄰接矩陣建立各目標動態模型,使用GLMB濾波算法獲得各目標的狀態估計和航跡估計;3)利用每時刻各目標的估計狀態獲得群的鄰接矩陣估計;4)通過連通圖估計獲得每時刻的子群個數估計.仿真實驗表明,上述方法能夠有效跟蹤可分辨群目標,但是由于目標剛出生的權重比較小,因此需要量測信息進行不斷更新,即信息累積的過程,并且量測具有延遲性,從而導致當目標個數發生改變時,算法對目標的個數估計會出現延遲現象.

1 Bar-Shalom Y,Tse E.Tracking in a cluttered environment with probabilistic data association.Automatica,1975,11(5):451?460

2 Bar-Shalom Y.Tracking methods in a multitarget environment.IEEE Transactions on Automatic Control,1978,23(4):618?626

3 Fortmann T,Bar-Shalom Y,Scheあe M.Sonar tracking of multiple targets using joint probabilistic data association.IEEE Journal of Oceanic Engineering,1983,8(3):173?184

4 Reid D.An algorithm for tracking multiple targets.IEEE Transactions on Automatic Control,1979,24(6):843?854

5 Blackman S.Multiple hypothesis tracking for multiple target tracking.IEEE Aerospace and Electronic Systems Magazine,2004,19(1):5?18

6 Salmond D J,Gordon N J.Group and extended object tracking.In:Proceedings of the 1999 IEE Colloquium on Target Tracking:Algorithms and Applications.London,UK:IEEE,1999.16/1?16/4

7 Liu Wei-Feng,ChaiZhong,Wen Cheng-Lin.Multimeasurement target tracking by using random sampling approach.Acta Automatica Sinica,2013,39(2):168?178(劉偉峰,柴中,文成林.基于隨機采樣的多量測目標跟蹤算法.自動化學報,2013,39(2):168?178)

8 Koch J W.Bayesian approach to extended object and cluster tracking using random matrices.IEEE Transactions on Aerospace and Electronic Systems,2008,44(3):1042?1059

9 Koch W,Van Keuk G.Multiple hypothesis track maintenance with possibly unresolved measurements.IEEE Transactions on Aerospace and Electronic Systems,1997,33(3):883?892

10 Feldmann M,Franken D,Koch W.Tracking of extended objects and group targets using random matrices.IEEE Transactions on Signal Processing,2011,59(4):1409?1420

11 Huang Jian,Hu Wei-Dong.Tracking of group space objects within Bayesian framework.Journal of Radars,2013,2(1):86?96(黃劍,胡衛東.基于貝葉斯框架的空間群目標跟蹤技術.雷達學報,2013,2(1):86?96)

12 Li Zhen-Xing,Liu Jin-Mang,Li Song,Bai Dong-Ying,Ni Peng.Group targets tracking algorithm based on box particle fi lter.Acta Automatica Sinica,2015,41(4):785?798(李振興,劉進忙,李松,白東穎,倪鵬.基于箱式粒子濾波的群目標跟蹤算法.自動化學報,2015,41(4):785?798)

13 Baum M,Hanebeck U D.Random hypersurface models for extended object tracking.In:Proceedings of the 9th IEEE International Symposium on Signal Processing and Information Technology(ISSPIT).Ajman,United Arab Emirates:IEEE,2009.178?183

14 Gilholm K,Salmond D.Spatial distribution model for tracking extended objects.IEEE Proceedings-Radar,Sonar and Navigation,2005,152(5):364?371

15 Gilholm K,Godsill S,Maskell S,Salmond D.Poisson models for extended target and group tracking.In:Proceedings of the 2005 SPIE 5913,Signal and Data Processing of Small Targets.San Diego,USA:SPIE,2005.230?241

16 Mahler R.PHD fi lters for nonstandard targets,I:extended targets.In:Proceedings of the 12th International Conference on Information Fusion.Seattle,USA:IEEE,2009.915?921

17 Lundquist C,Granstr¨om K,Orguner U.Estimating the shape of targets with a PHD fi lter.In:Proceedings of the 14th International Conference on Information Fusion(FUSION).Chicago,USA:IEEE,2011.49?56

18 Granstr¨om K,Lundquist C,Orguner U.A Gaussian mixture PHD fi lter for extended target tracking.In:Proceedings of the 13th International Conference on Information Fusion(FUSION).Edinburgh,UK:IEEE,2010.1?8

19 Orguner U,Lundquist C,Granstr¨om K.Extended target tracking with a cardinalized probability hypothesis density fi lter.In:Proceedings of the 14th International Conference on Information Fusion(FUSION).Chicago,USA:IEEE,2011.65?72

20 Lian Feng,Han Chong-Zhao,Liu Wei-Feng,Yuan Xiang-Hui.Tracking partly resolvable group targets using SMCPHDF.Acta Automatica Sinica,2010,36(5):731?741(連峰,韓崇昭,劉偉峰,元向輝.基于SMC-PHDF的部分可分辨的群目標跟蹤算法.自動化學報,2010,36(5):731?741)

21 Lian Feng,Ma Dong-Dong,Yuan Xiang-Hui,Chen Wen,Han Chong-Zhao.CBMeMBer fi lter for extended targets and its Gaussian mixture implementations.Control and Decision,2015,30(4):611?616(連峰,馬冬冬,元向輝,陳文,韓崇昭.擴展目標CBMeMBer濾波器及其高斯混合實現.控制與決策,2015,30(4):611?616)

22 Gning A,Mihaylova L,Maskell S,Pang S K,Godsill S.Group object structure and state estimation with evolving networks and Monte Carlo methods.IEEE Transactions on Signal Processing,2011,59(4):1383?1396

23 Ristic B,Sherrah J.Bernoulli fi lter for joint detection and tracking of an extended object in clutter.IET Radar,Sonar,and Navigation,2013,7(1):26?35

24 Vo B T,Vo B N.Labeled random fi nite sets and multi-object conjugate priors.IEEE Transactions on Signal Processing,2013,61(13):3460?3475

25 Vo B N,Vo B T,Phung D.Labeled random fi nite sets and the Bayes multi-target tracking fi lter.IEEE Transactions on Signal Processing,2014,62(24):6554?6567

26 Beard M,Reuter S,Granstrom K,Vo B T,Vo B N,Scheel A.A generalised labelled multi-Bernoulli fi lter for extended multi-target tracking.In:Proceedings of the 18th International Conference on Information Fusion(FUSION).Washington,USA:IEEE,2015.991?998

27 Zhu S J,Liu W F,Weng C L,Cui H L.Multiple group targets tracking using the generalized labeled multi-Bernoulli fi lter.In:Proceedings of the 35th Chinese Control Conference.Chengdu,China:IEEE,2016.4871?4876

28 Mahler R P S.Multitarget Bayes fi ltering via fi rst-order multitarget moments.IEEE Transactions on Aerospace and Electronic Systems,2003,39(4):1152?1178

29 Mahler R P S.Statistical Multisource-Multitarget Information Fusion.Boston,USA:Artech House,2007.

30 Anderson B D O,Yu C B,Fidan B,Hendrickx J M.Control and information architectures for formations.In:Proceedings of the 2006 IEEE Conference on Computer Aided Control System Design,2006 IEEE International Conference on Control Applications,2006 IEEE International Symposium on Intelligent Control.Munich,Germany:IEEE,2006.1127?1138

31 Yu C B,Hendrickx J M,Fidan B,Anderson B D O,Blondel V D.Three and higher dimensional autonomous formations:rigidity,persistence and structural persistence.Automatica,2007,43(3):387?402

32 Diestel R.Graph Theory(3rd edition).New York:Spring-Verlag,2005.

33 Chung F.Lecture Notes on Spectral Graph Theory.Providence,RI:AMS Publications,1997.

34 Vo B T,Vo B N,Cantoni A.The cardinality balanced multitarget multi-Bernoulli fi lter and its implementations.IEEE Transactions on Signal Processing,2009,57(2):409?423

35 Schuhmacher D,Vo B T,Vo B N.A consistent metric for performance evaluation of multi-object fi lters.IEEE Transactions on Signal Processing,2008,56(8):3447?3457

Multiple Resolvable Groups Tracking Using the GLMB Filter

ZHU Shu-Jun1LIU Wei-Feng1,2CUI Hai-Long1

Aiming at the estimation of states,the number of targets and subgroups,a resolvable group target tracking algorithm is proposed based on the framework of label random fi nite set(L-RFS).The proposed algorithm focus on two aspects:dynamic modeling and tracking estimation for multiple resolvable group targets.Speci fi cally,in the fi rst step,the adjacent matrix is fused in the dynamic models.In the second step,the estimated state sets of the targets and the number of targets are estimated by using the generalized labeled multi-Bernoulli(GLMB) fi lter in the L-RFS framework.Finally,from the estimated adjacent matrix,the structures and number of subgroups are shown.Two experiments of a linear system and a nonlinear system,which involve three groups of targets with diあerent shapes and structure,are given to show that the given algorithm is eあective in estimating the resolvable group targets.

Resolvable group target tracking,generalized label multi-Bernoulli(GLMB),adjacent matrix,random fi nite set(RFS),graph theory

Zhu Shu-Jun,Liu Wei-Feng,Cui Hai-Long.Multiple resolvable groups tracking using the GLMB fi lter.Acta Automatica Sinica,2017,43(12):2178?2189

2016-04-15 錄用日期2016-12-27

April 15,2016;accepted December 27,2016

國家自然科學基金(61333011,61271144,61273170,61402140),浙江省自然科學基金(LY15F030020),杭州電子科技大學控制科學與工程重點學科資助

Supported by National Natural Science Foundation of China(61333011,61271144,61273170,61402140),Natural Science Foundation of Zhejiang Province(LY15F030020),and Most Important Subjects of Control Science and Engineering of Hangzhou Dianzi University

本文責任編委郭戈

Recommended by Associate Editor GUO Ge

1.杭州電子科技大學自動化學院系統科學與控制工程研究所 杭州310018 2.信息系統工程重點實驗室 南京210007

1.Institute of Systems Science and Control Engineering,School of Automation,Hangzhou Dianzi University,Hangzhou 310018 2.Science and Technology on Information System Engineering Laboratory,Nanjing 210007

朱書軍,劉偉峰,崔海龍.基于廣義標簽多伯努利濾波的可分辨群目標跟蹤算法.自動化學報,2017,43(12):2178?2189

DOI10.16383/j.aas.2017.c160334

朱書軍 杭州電子科技大學自動化學院系統科學與控制工程研究所碩士研究生.2014年獲得麗水學院學士學位.主要研究方向為目標跟蹤與信息融合.

E-mail:zsjun92@163.com

(ZHU Shu-Jun Master student at the Institute of Systems Science and Control Engineering,School of Automation,Hangzhou Dianzi University.He received his bachelor degree from Lishui University in 2014.His research interest covers target tracking and information fusion.)

劉偉峰 杭州電子科技大學副教授.主要研究方向為目標跟蹤,不確定信息處理與模式識別.本文通信作者.

E-mail:liuwf@hdu.edu.cn

(LIU Wei-Feng Associate professor at Hangzhou Dianzi University.His research interest covers target tracking,uncertain information processing,and pattern recognition.Corresponding author of this paper.)

崔海龍 杭州電子科技大學自動化學院系統科學與控制工程研究所碩士研究生.2014年獲得安徽工程大學學士學位.主要研究方向為目標跟蹤與信息融合.

E-mail:cuihailong86@163.com

(CUI Hai-Long Master student at the Institute of Systems Science and Control Engineering,School of Automation,Hangzhou Dianzi University.He received his bachelor degree from Anhui Polytechnic University in 2014.His research interest covers target tracking and information fusion.)