一類微生物流加發酵過程的動態優化

王 丹，李彩霞，徐恭賢

(渤海大學 數理學院， 遼寧 錦州 121013)

一類微生物流加發酵過程的動態優化

王 丹，李彩霞，徐恭賢

(渤海大學 數理學院， 遼寧 錦州 121013)

研究了甘油生物歧化為1，3-丙二醇的流加發酵過程。針對甘油生物歧化為1，3-丙二醇過程的流加發酵系統，建立了在終端時刻是固定值的前提下，以1，3-丙二醇的濃度達到最大值為目標函數的動態優化模型。采用有限元配置法，將甘油流加生物歧化為1，3-丙二醇過程的狀態方程轉換為代數方程，進而得到模型的NLP(非線性規劃)形式。運用Matlab軟件求解所建立的動態優化模型，并針對所得到的優化結果進行分析及討論。

1，3-丙二醇；動態優化；流加發酵；有限元配置法

1，3-丙二醇是一種非常重要的化工原料，如溶劑、抗凍劑或保護劑、精細化工原料以及聚合物單體等[1-2]。與傳統的化學合成法相比，微生物法具有轉化率高、副產物少、環境污染小等優點[3]，但要提高1，3-丙二醇的濃度依然是很難解決的問題。因此，甘油生物歧化生產1，3-丙二醇日益受到關注。

近年來，越來越多的學者們熱衷于對甘油歧化微生物生產1，3-丙二醇過程的研究。楊杰通過建立單目標和多目標動態優化模型，研究了微生物間歇發酵生產1，3-丙二醇過程的優化問題[4]。徐恭賢等對發酵過程提出新的迭代優化策略，并且進行優化控制的研究[5]。孫亞琴等[6]建立了甘油生物歧化為1，3-丙二醇過程還原途徑酶催化8維非線性動力系統。宮召華等[7]建立了最優控制模型，利用不可微優化理論得到了最優控制問題的最優性條件，并證明了最優性條件和最優性函數零點的等價性。譚雯心[8]建立了以各代謝物的濃度誤差與斜率誤差之和為目標函數的參數辨識動態優化模型。文獻[9-12]等基于代謝工程方法對主要產物1，3-丙二醇的生產改善問題進行了研究。高群王等[13]提出了一個使主要產物1，3-丙二醇產率達到最大的穩態優化模型。文獻[14-16]研究了甘油連續生物歧化為1，3-丙二醇過程的多目標優化問題。徐恭賢等[17]研究了甘油間歇生物歧化過程的動態優化，獲得更高的1，3-丙二醇產率。

本文針對微生物流加發酵生產1，3-丙二醇過程的動態優化問題，建立與其過程特點相適應的動態優化模型，并提出有效的算法求解該模型，結果表明方法有效。

1 流加發酵過程的數學模型

微生物流加過程的方程式描述如下：

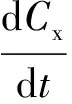
(1)

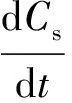
(2)

(3)

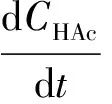
(4)

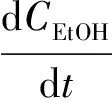
(5)

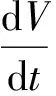
(6)

(7)

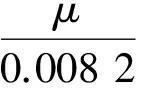
(8)

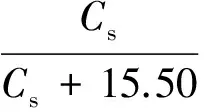
(9)

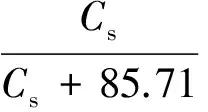
(10)

(11)

t∈[0,tf]

(12)

其中：Cx是生物量(g·L-1)；μ和μm分別是比生長速率及其最大值(h-1)；Cs是底物濃度(mmol·L-1)；CPD，CHAc，CEtOH是產物濃度(mmol·L-1)；t是發酵時間(h)；qs是底物比消耗速率(mmol·g-1·h-1)；qPD，qHAc，qEtOH是產物比生成速率(mmol·g-1·h-1)；F是甘油流加速率 (L·h-1)；V是反應器中液體體積(L)；r是堿的流加速率與甘油流加速率的比。

2 優化模型

以終端時刻是固定值為前提，1，3-丙二醇的濃度達到最大為目標函數，建立如下動態優化模型：

maxf=CPD(tf)

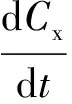
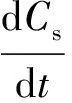
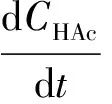
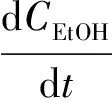
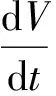
(13)

0≤t≤tf

0≤Cx≤5

0≤Cs≤2 039

0≤CPD≤939.5

0≤CHAc≤1 026

0≤CEtOH≤360.9

5≤V≤8

0≤F≤0.9

3 有限元配置法

為了方便敘述，設x=(x1,x2,x3,x4,x5,x6)T=(Cx,Cs,CPD,CHAc,CEtOH,V)T

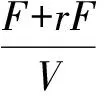
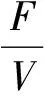
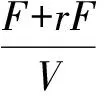
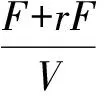
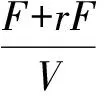
f6(x)=F+rF

G(x(tf),tf)=CPD(tf)

u(t)=F

則可將問題(13)表示為下列優化問題：

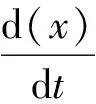
x≤(5,2039,939.5,1026,360.9,VU)T

x≥(0,0,0,0,0,VL)T

(14)

u(t)L≤u(t)≤u(t)U

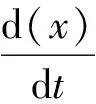
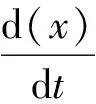
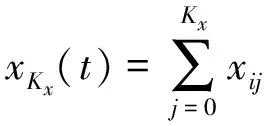
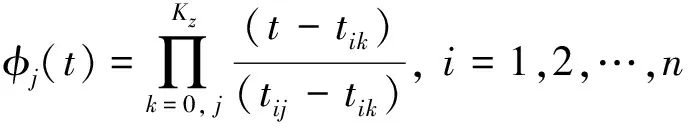
(15)

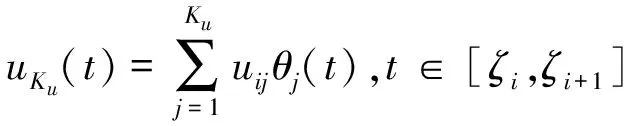
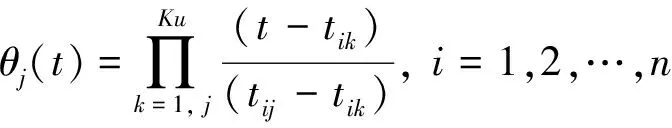
(16)

其中：Kx為有限元[ζi,ζi+1]上配置點的個數。拉格朗日多項式xKx(t)滿足xKx(tij)=xij，uKu(t)滿足uKu(tij)=uij。為了確定拉格朗日多項式xKx(t),uKu(t)的系數，將其代入狀態方程中，則可得配置方程：

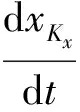
k=1,2,…,Kx

(17)

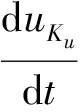
k=1,2,…,Ku

(18)

令tik=ζi+Δζiτk, Δζi=ζi+1-ζi,τk∈[0,1]，則可將式(17)、(18)寫為：

k=1,2,…,Kx

(19)

k=1,2,…,Ku

(20)

另外，為了確保狀態在有限元終端處具有連續性，相鄰有限元的初始狀態和終端狀態需滿足以下條件：

基于上述分析可將動態優化問題(14)轉化為如下NLP問題：

i=1,2,…,n,j=0,1,…,Kx

i=1,2,…,n,j=0,1,…,Ku

(21)

i=1,2,…,n,j=1,2,…,Ku

xKx(tij)≤(5,2039,939.5,1026,360.9,VU)T,

xKx(tij)≥(0,0,0,0,0,VL)T

i=1,2,…,n,j=1,2,…,Kx

4 優化結果與分析

本文在Matlab上用其優化工具箱求解NLP問題(21)。表1 給出不同的終端時刻下，動態優化問題的最優解。如表1所示，隨終端時刻tf逐漸增大，Cx(tf)逐漸減小，最小值為1.79 mmol·L-1；Cs(tf)先逐漸增大，然后減小，在31 h升到最大1 186.68 mmol·L-1；CPD(tf)始終可達到最大值939.5 mmol·L-1；CHAc(tf)的值先減小，在終端時刻為25 h時，增大至230.63 mmol·L-1，然后逐漸降低；CEtOH(tf)、V(tf)和F的值都是先增大，在20 h到28 h內逐漸減小，然后增大，CEtOH(tf)最大可達到139.99 mmol·L-1，V(tf)在終端時刻為28 h時達到最大值7.57 mmol·L-1，F最大可達到0.41 mmol·L-1。

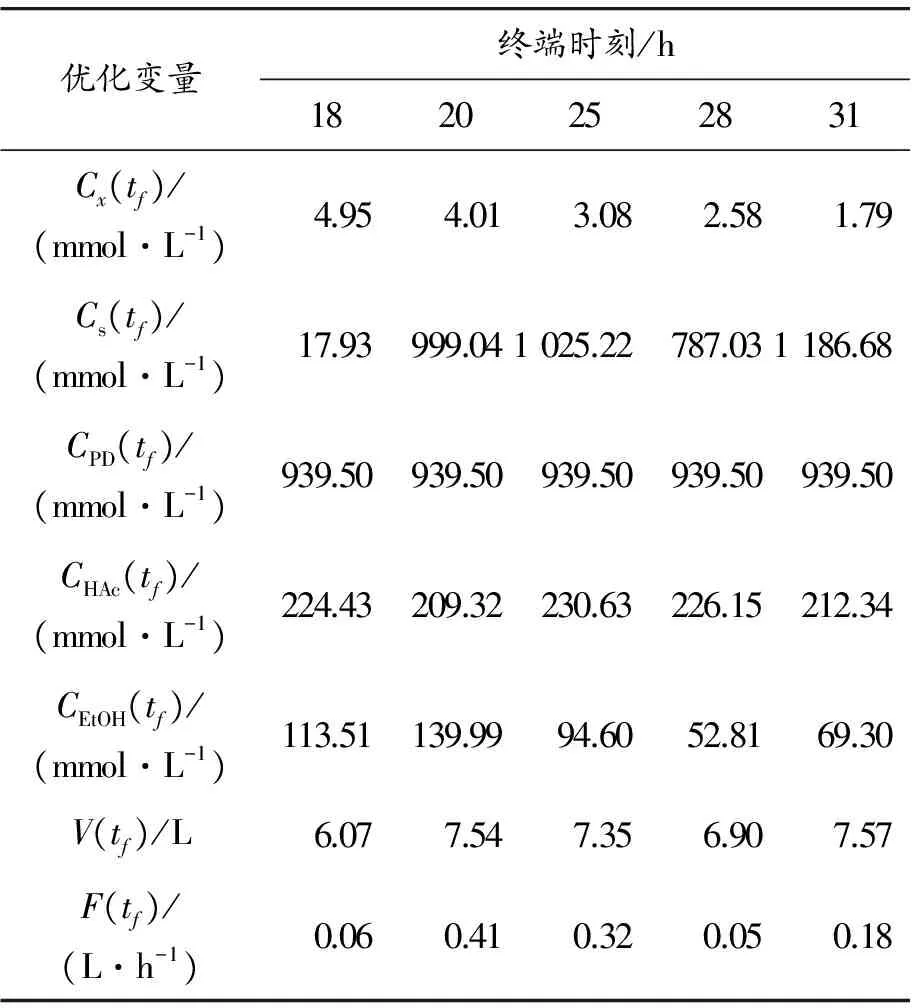
表1 不同終端時刻動態優化問題的最優解

圖1～7為終端時刻取20 h時，底物和產物隨發酵時間t的變化曲線。

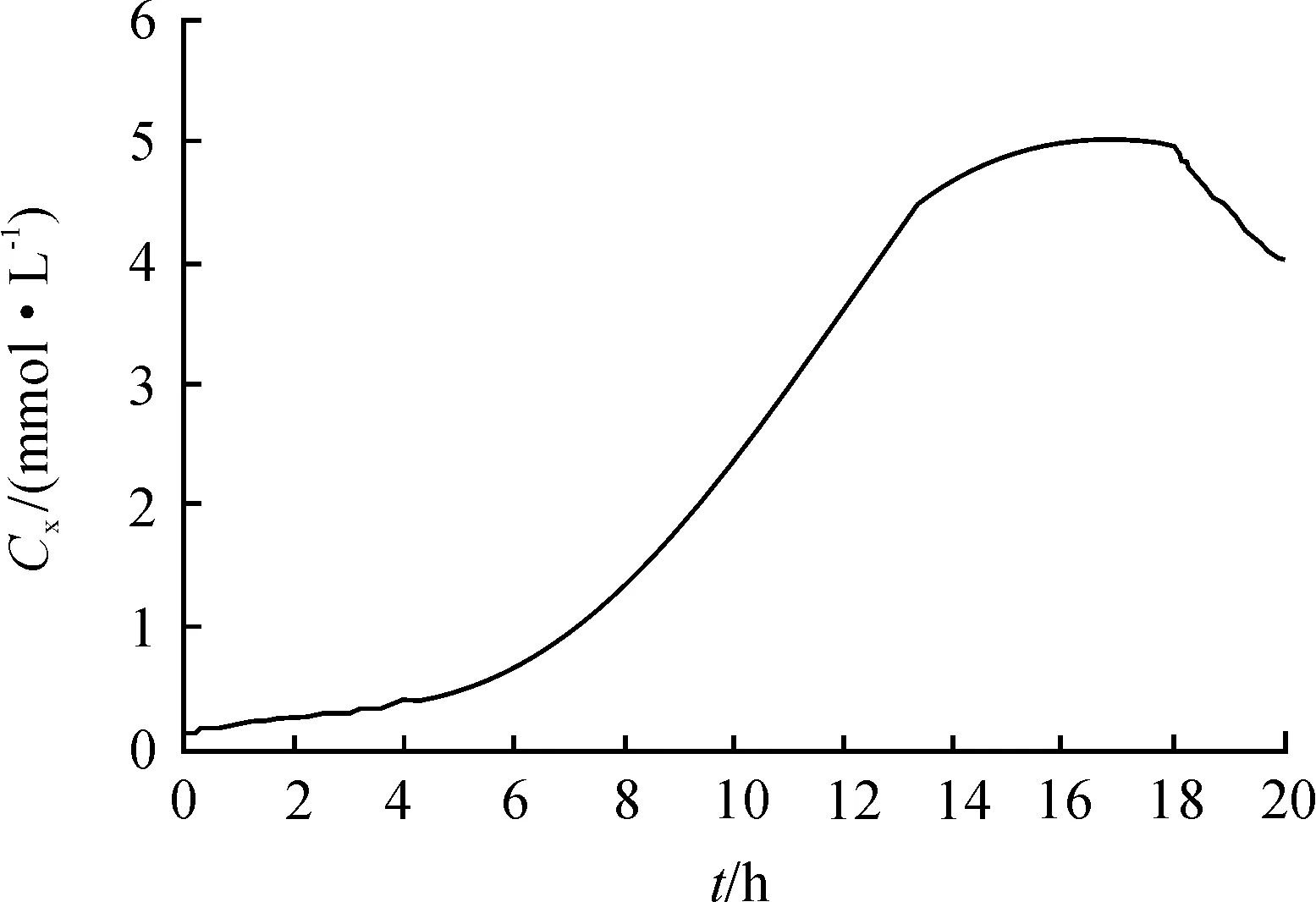
圖1 生物量的變化曲線

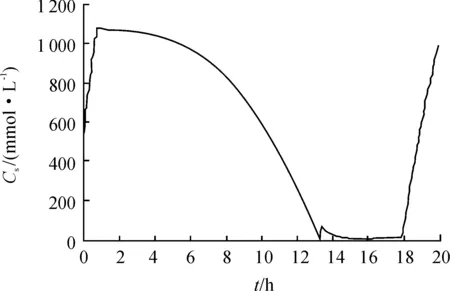
圖2 甘油濃度的變化曲線

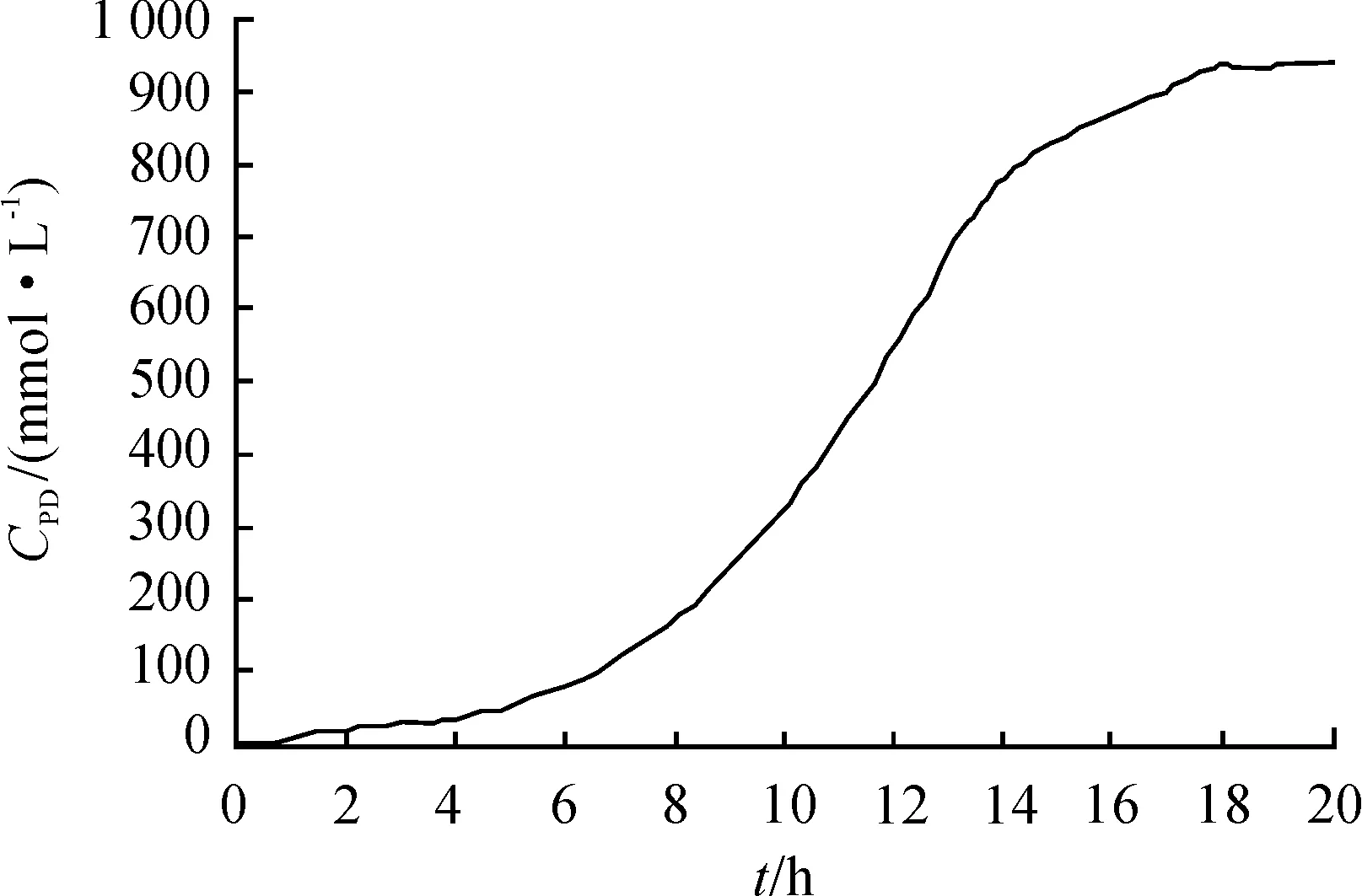
圖3 1，3-丙二醇濃度的變化曲線

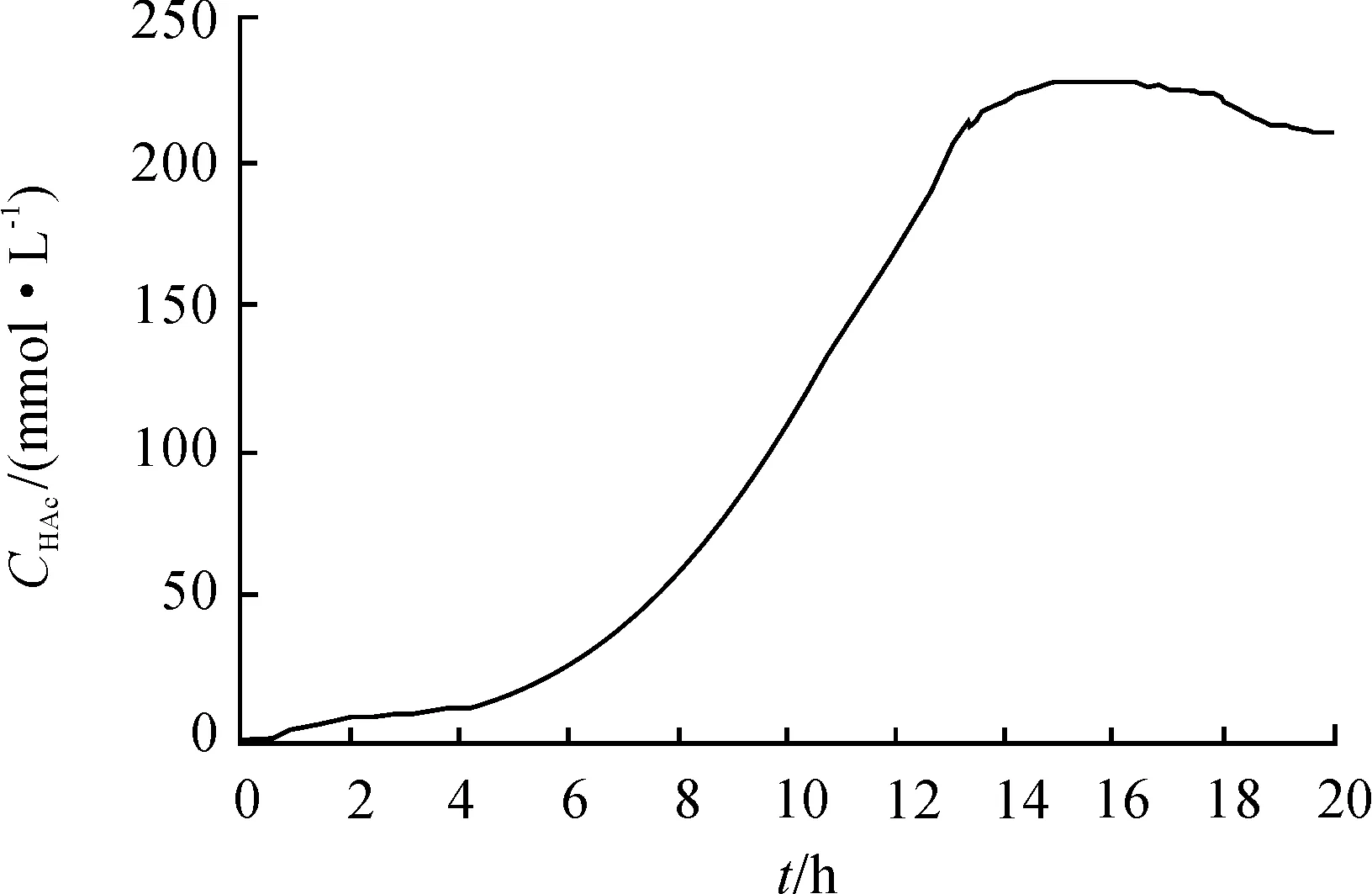
圖4 乙酸濃度的變化曲線

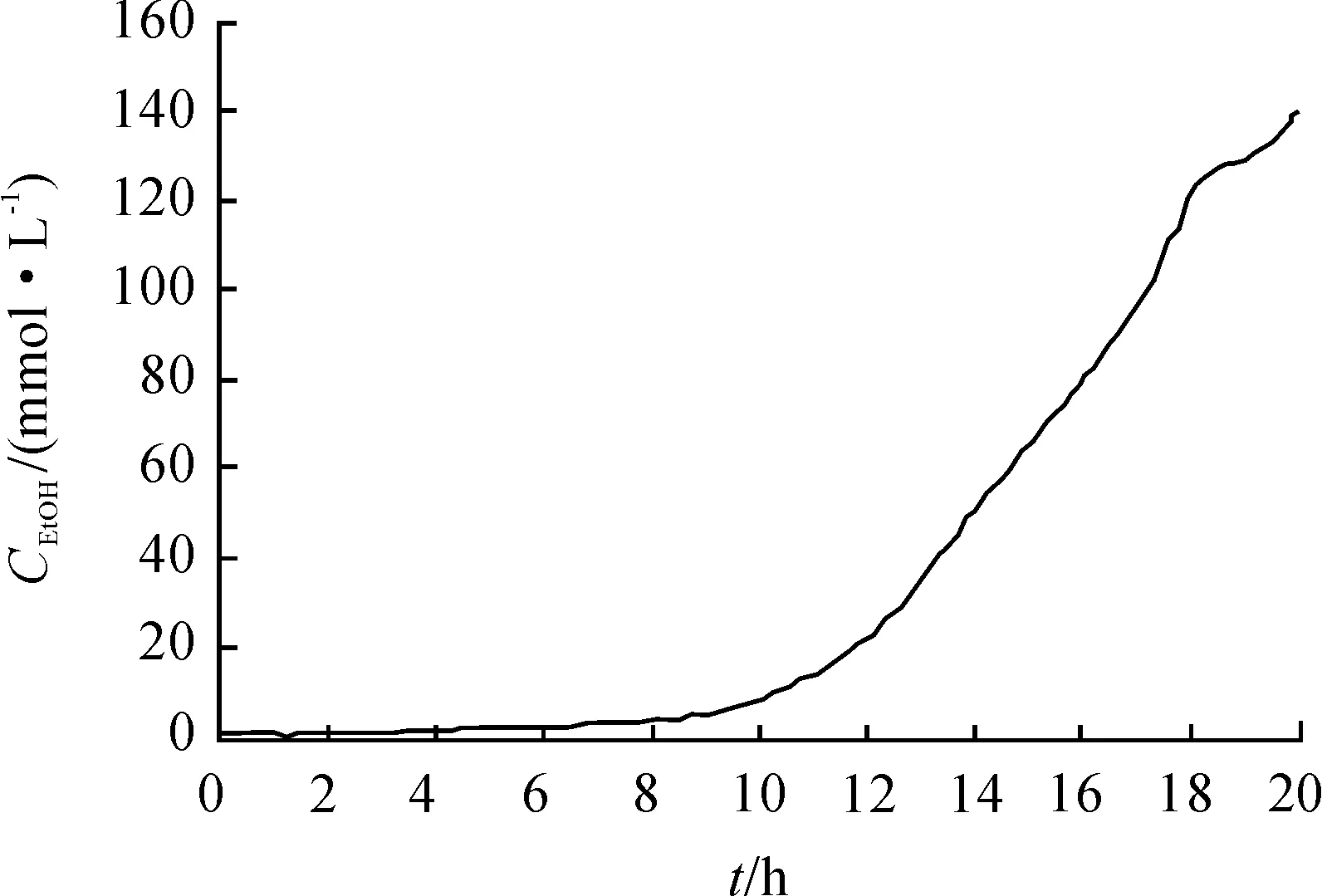
圖5 乙醇濃度的變化曲線

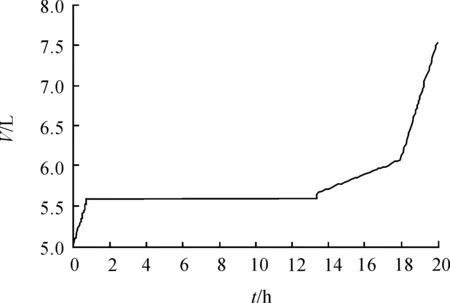
圖6 反應器中液體體積的變化曲線

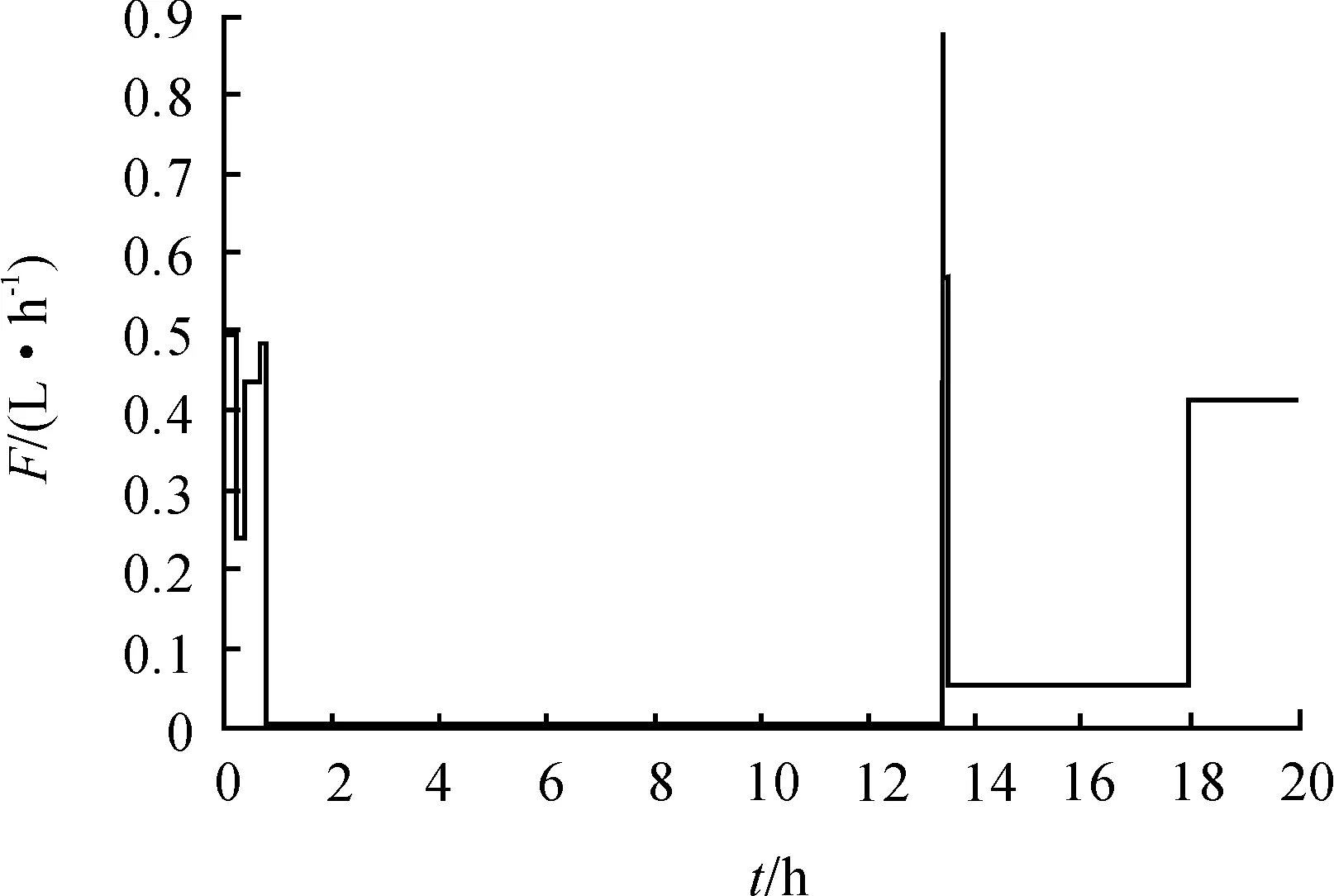
圖7 甘油流加速率的變化曲線

5 結束語

本文針對甘油流加生物歧化生產1，3-丙二醇的過程，研究了其動態優化問題。以終端時刻產物1，3-丙二醇的濃度作為目標函數，提出了動態優化模型，并利用有限元配置法結合Matlab軟件求解了所提出的優化問題。本文通過取不同的終端時刻值，獲得底物消耗和產物生成的變化情況，為實現甘油流加生物歧化過程的工業生產優化提供了指導。計算結果表明：終端時刻1，3-丙二醇的濃度可達到其最大允許值。

[1] 孫亞琴.甘油生物歧化過程酶催化和基因調控的非線性數學模擬與分析[D].大連:大連理工大學，2010.

[2] 修志龍.1,3-丙二醇的微生物法生產分析[J].現代化工，1999，19(3):33-35.

[3] 徐恭賢，邵誠，錢偉懿.非線性生化過程的優化與控制[M].北京:科學出版社，2015.

[4] 楊杰.一類微生物發酵過程的動態優化[D].錦州:渤海大學，2015.

[5] XU G X，SHAO C，XIU Z L.Optimizing control of bio-dissimilation process of glycerol to 1，3-propanediol[J].Chinese Journal of Chemical Engineering，2008，16(1):128-134.

[6] SUN Y Q，QI W T，TENG H，et al.Mathematical modeling of glycerol fermentation by Klebsiella pneumoniae:Concerning enzyme-catalytic reductive pathway and transport of glycerol and 1，3-propanediol across cell membrane[J].Biochemical Engineering Journal，2008，38:22-32.

[7] 宮召華，馮恩民.微生物批式流加發酵多階段最優控制的最優性條件[J].運籌學學報，2009，13(4):109-119.

[8] 徐恭賢，譚雯心，王佳星.一類微生物間歇發酵過程的參數辨識[J].重慶理工大學學報(自然科學)，2016(10):76-80.

[9] KUMAR V，DURGAPAL M，SANKARANARAYANAN M，et al.Effects of mutation of 2，3-butanediol formation pathway on glycerol metabolism and 1，3-propanediol production by Klebsiella pneumoniae J2B[J].Bioresource Technology，2016，214:432-440.

[10] CHEN Z,LIU H J，LIU D H.Metabolic pathway analysis of 1，3-propanediol production with a genetically modified Klebsiella pneumoniae by overexpressing an endogenous ADPH-dependent alcohol dehydrogenase[J].Biochemical Engineering Journal，2011，54(3):151-157.

[11] WISCHRAL D，ZHANG J，CHENG C，et al.Production of 1，3-propanediol by Clostridium beijerinckii DSM 791 from crude glycerol and corn steep liquor： Process optimization and metabolic engineering[J].Bioresource Technology，2016，212:100-110.

[12] HIROKAWA Y，MAKI Y，TATSUKE T，et al.Cyanobacterial production of 1，3-propanediol directly from carbon dioxide using a synthetic metabolic pathway[J].Metabolic Engineering，2016，34:97-103.

[13] 高群王，徐恭賢，王佳星.一類生物過程的穩態優化[J].重慶理工大學學報(自然科學)，2015(10):152-158.

[14] ZENG A P，XIU Z L，AN L J.Mathematical modeling of kinetics and research on multiplicity of glycerol bioconversion to 1，3-propanediol[J].Journal of Dalian University of Technology，2000，40(4):428-433.

[15] TAG C G.Mikrobielle herstellung von 1，3-propanediol[D].Oldenburg:University of Oldenburg，1990.

[16] 高群王，李楊，宋一凡，等.一類連續生物過程的雙目標優化[J].渤海大學學報(自然科學版)，2016,37(3):152-158.

[17] 徐恭賢，楊杰.甘油間歇生物歧化過程的動態優化[J].計算機工程與應用，2017，53(10):258-263.

[18] BIEGLER L T.Nonlinear programming:Concepts，algorithm，and applications to chemical processes[M].Philadelphia:SIAM，2010.

DynamicOptimizationforaClassofMicrobialFed-BatchFermentationProcess

WANG Dan， LI Caixia， XU Gongxian

(College of Mathematics and Physics, Bohai University, Jinzhou 121013, China)

The fed-batch fermentation process of glycerol bio-dissimilation to 1, 3-propanediol was studied. A dynamic optimization model with the maximum concentration of 1, 3-propanediol as the objective function was established under the premise that the terminal time was a fixed value for the fed-batch fermentation system with glycerol bio-dissimilation as 1, 3-propanediol. The NLP (nonlinear programming) form of the model was obtained by using collocation on finite elements method to convert the state equation of the glycerol bio-dissimilation to the 1, 3-propanediol process to the algebraic equation. The dynamic optimization model was solved by Matllab software, and the optimization results were analyzed and discussed.

1, 3-propanediol; dynamic optimization; fed-batch fermentation; collocation on finite elements method

2017-06-10

國家自然科學基金資助項目(11101051，11371071)；遼寧省自然科學基金資助項目(2015020038)

王丹(1993—),女,黑龍江五大連池人,碩士研究生,主要從事最優化方法與應用研究，E-mail:844364936@qq.com；通訊作者 徐恭賢(1976—)，男，遼寧莊河人,博士,副教授,主要從事最優化方法與應用方面的研究，E-mail:gxxu@bhu.edu.cn。

王丹，李彩霞，徐恭賢.一類微生物流加發酵過程的動態優化[J].重慶理工大學學報(自然科學)，2017(12):116-121.

formatWANG Dan， LI Caixia， XU Gongxian.Dynamic Optimization for a Class of Microbial Fed-Batch Fermentation Process[J].Journal of Chongqing University of Technology(Natural Science)，2017(12):116-121.

10.3969/j.issn.1674-8425(z).2017.12.020

O29

A

1674-8425(2017)12-0116-06

(責任編輯何杰玲)