一種改進(jìn)的組合導(dǎo)航系統(tǒng)選星算法

馮 彪，柴洪洲，潘宗鵬，王 敏，楊克凡

(信息工程大學(xué)，河南 鄭州 450000)

一種改進(jìn)的組合導(dǎo)航系統(tǒng)選星算法

馮 彪，柴洪洲，潘宗鵬，王 敏，楊克凡

(信息工程大學(xué)，河南 鄭州 450000)

針對GPS，GLONASS，BDS組合導(dǎo)航系統(tǒng)定位中衛(wèi)星的選擇作了相關(guān)分析。首先用STK軟件進(jìn)行仿真，分析幾何精度因子與衛(wèi)星數(shù)的關(guān)系，得出組合導(dǎo)航系統(tǒng)最佳選星數(shù)；再根據(jù)衛(wèi)星星座的空間幾何分布，基于次優(yōu)選星算法的成本函數(shù)模型，結(jié)合各導(dǎo)航系統(tǒng)衛(wèi)星測量精度的差異性以及次優(yōu)選星算法的峰值、不穩(wěn)定特點(diǎn)，構(gòu)建一種以衛(wèi)星高度角和載噪比確定的加權(quán)成本函數(shù)模型，提出一種依據(jù)加權(quán)成本函數(shù)選星的分步次優(yōu)加權(quán)選星算法。實(shí)驗(yàn)結(jié)果表明，該選星算法能近似到達(dá)最優(yōu)選星算法的效果，計(jì)算負(fù)荷也相對較小，可滿足導(dǎo)航定位解算精度和實(shí)時(shí)性要求。

組合導(dǎo)航系統(tǒng)；STK；GDOP；加權(quán)成本函數(shù)模型；分步次優(yōu)加權(quán)選星算法

隨著全球衛(wèi)星導(dǎo)航系統(tǒng)(Global Navigation Satellite System，GNSS)不斷發(fā)展，不同衛(wèi)星星座間的組合，提供的可見衛(wèi)星數(shù)目逐漸增多，衛(wèi)星的幾何分布結(jié)構(gòu)也更完善。相對于單星座而言，多星座衛(wèi)星組合導(dǎo)航系統(tǒng)的精度、完好性、可用性及可靠性都將大大的提高。但由于可見衛(wèi)星數(shù)的成倍增長，會(huì)造成冗余信息過多，隨之導(dǎo)航定位的計(jì)算量將成幾十倍增長，嚴(yán)重影響導(dǎo)航定位解算的實(shí)時(shí)性，也對多模接收機(jī)的通道數(shù)和處理速度提出更高要求，也大大增加了接收機(jī)硬件設(shè)計(jì)的難度和成本。因此，在保證用戶導(dǎo)航定位精度的前提下，減少冗余信息和降低導(dǎo)航定位解算的運(yùn)算量，均衡地處理兩者間的關(guān)系，選取分布合理的衛(wèi)星就顯得至關(guān)重要。

通常情況下，選星是要找出幾何精度因子(Geometric Dilution of Precision, GDOP)最小的衛(wèi)星組合，關(guān)鍵是綜合考慮定位精度和實(shí)時(shí)性，確定選星數(shù)目和設(shè)計(jì)選星算法[1]。常規(guī)選星算法：最小GDOP值法[2]，即最優(yōu)選星算法，衛(wèi)星數(shù)較多時(shí)，運(yùn)算量巨大；最大多面體體積法[3]、最大行列式法[4]是根據(jù)GDOP值隨多面體體積與觀測矩陣的行列式值的大小成反比原則選星，但GDOP值分別與多面體體積、矩陣行列式大小間的比例關(guān)系并不嚴(yán)格單調(diào)[5-6]，計(jì)算量也較大；基于衛(wèi)星高度角和方位角選星算法[7]和應(yīng)用模糊數(shù)學(xué)理論選星法[8]是根據(jù)衛(wèi)星幾何分布選星，需事先知道頂星座和底星座衛(wèi)星個(gè)數(shù)，挑選方位角分布均勻的衛(wèi)星，但衛(wèi)星間方位角角差近似判斷標(biāo)準(zhǔn)不易明確，而運(yùn)用模糊數(shù)學(xué)理論過程又太繁瑣復(fù)雜；組合選星法[9]選星結(jié)果最接近最小GDOP值法，但衛(wèi)星數(shù)較多時(shí)，行列式計(jì)算量仍很大；間接選星法[10]，通過對高、低仰角區(qū)衛(wèi)星數(shù)的判斷，采用逆向思維反選出不要的衛(wèi)星，同樣存在選星數(shù)較多時(shí)，計(jì)算量大，不易實(shí)時(shí)應(yīng)用的問題。

1 幾何精度因子GDOP及影響因素

衛(wèi)星導(dǎo)航系統(tǒng)的定位精度，可以表示為幾何精度因子和用戶等效距離誤差的乘積，即

σP=GDOP·σUERE.

(1)

式中：σP表示定位精度的標(biāo)準(zhǔn)偏差；GDOP表示幾何精度因子；σURER表示用戶等效距離誤差的標(biāo)準(zhǔn)差。GDOP表征用戶和可見衛(wèi)星的空間幾何分布情況，反映定位衛(wèi)星星座的拓?fù)浣Y(jié)構(gòu)對用戶等效距離誤差的放大程度，是作為衡量導(dǎo)航系統(tǒng)定位性能的重要指標(biāo)。

幾何精度因子是衛(wèi)星與用戶幾何分布的函數(shù)，為

(2)

式中：trace( * )表示對矩陣取跡；A為GPS，GLONASS，BDS組合系統(tǒng)的觀測矩陣，

(3)

(4)

式中：losj為衛(wèi)星j與用戶的觀測向量;n為衛(wèi)星系統(tǒng)i的衛(wèi)星數(shù)。

(5)

式中：elj，aj分別表示衛(wèi)星j的高度角和方位角。

由式(2)可知幾何精度因子與觀測矩陣A相關(guān)，取決于接收機(jī)與可見星的觀測向量的組合。衛(wèi)星幾何分布越佳，A陣條件數(shù)越低，GDOP值越小；反之，衛(wèi)星幾何分布越差，A陣條件數(shù)越高，GDOP值越大[11]。同時(shí)，當(dāng)可用衛(wèi)星較少、幾何分布又不理想時(shí)，A陣甚至可能呈病態(tài)，導(dǎo)致GDOP值極大，使解算失效；當(dāng)可見衛(wèi)星較多時(shí)，A陣為高階矩陣，求逆矩陣過程中矩陣運(yùn)算量巨大，冗余信息過量，導(dǎo)致實(shí)時(shí)性差。因此，導(dǎo)航解算的選星過程必須綜合考慮衛(wèi)星的幾何構(gòu)型和參與解算的最佳選星數(shù)目。

關(guān)于最佳選星數(shù)，本文通過STK(Satellite Tool Kit)軟件進(jìn)行仿真分析，時(shí)間為2015-12-09 08:00:00～23:59:30(GPST)，采樣間隔30s，可見星截止高度角15°，統(tǒng)計(jì)分析GPS，GLONASS，BDS組合系統(tǒng)GDOP值隨衛(wèi)星數(shù)的變化，以確定最佳選星數(shù)目。用戶位置分別選取位于中國區(qū)域的IGS(International GNSS Service)臺(tái)站bjfs，wuhn，xian，shao，kunm，tcms 9個(gè)臺(tái)站，臺(tái)站位置信息見表1。

表1 用戶位置信息

用STK模擬仿真了多星座組合系統(tǒng)分別選取6～18顆衛(wèi)星以及所有可見星下其最小GDOP值，相應(yīng)隨衛(wèi)星數(shù)變化曲線如圖1所示。6站可見衛(wèi)星數(shù)為22～29顆，均值為23～24 顆。

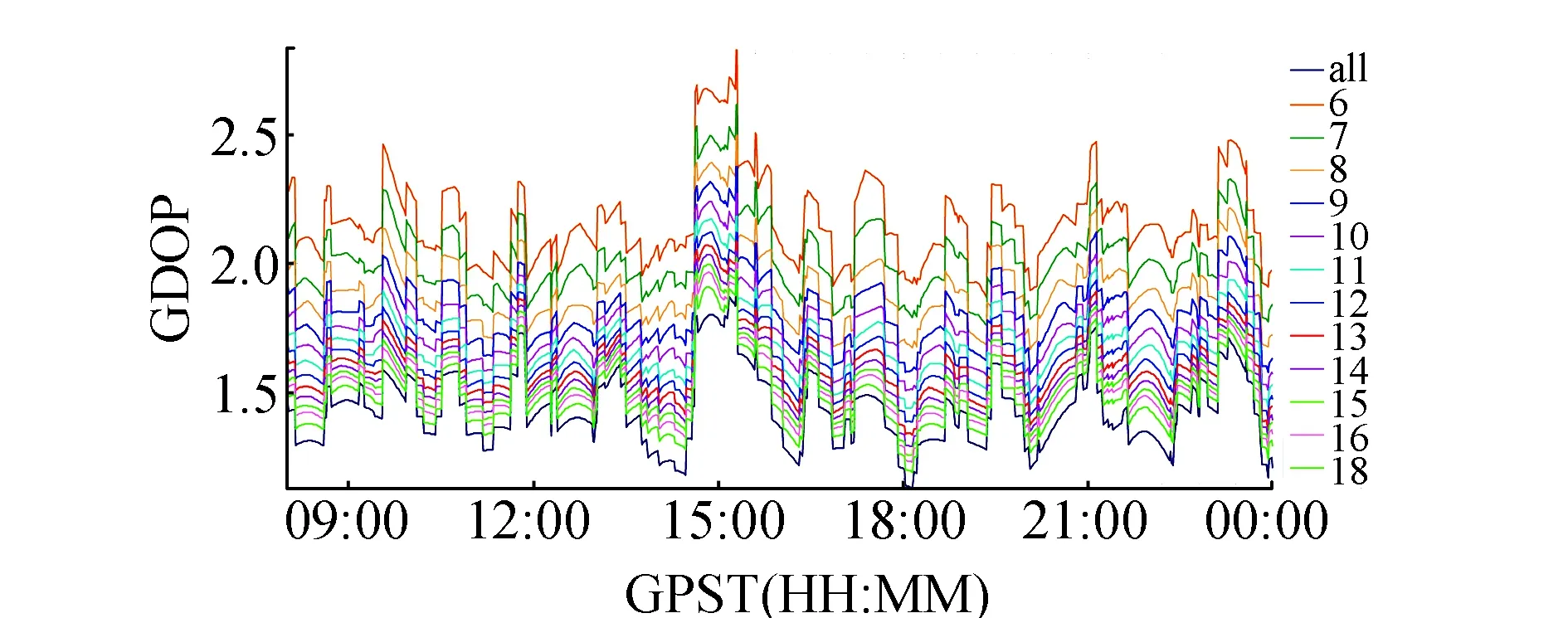
圖1 wuhn站GDOP值隨衛(wèi)星數(shù)的變化關(guān)系

圖2 均值與衛(wèi)星數(shù)SVs關(guān)系

2 分步次優(yōu)加權(quán)選星算法

2.1 次優(yōu)選星算法

次優(yōu)選星算法[12]是根據(jù)衛(wèi)星的幾何分布，通過比較兩兩衛(wèi)星觀測向量間的夾角大小評估衛(wèi)星的冗余信息，剔除冗余量大的衛(wèi)星，選出幾何分布較好的衛(wèi)星。冗余信息通過衛(wèi)星間的成本函數(shù)值估計(jì)，成本函數(shù)定義為

Cij=cos 2θij.

(6)

式中：θij表示衛(wèi)星i和衛(wèi)星j觀測向量間的夾角。當(dāng)兩顆衛(wèi)星之間夾角為0°或±180°時(shí)，即兩顆衛(wèi)星與接收機(jī)同時(shí)處于一條直線上，其成本函數(shù)值最大；當(dāng)兩衛(wèi)星夾角為90°時(shí)，也就是兩顆衛(wèi)星與用戶構(gòu)成一個(gè)直角三角形時(shí)，其成本函數(shù)值最小。而為了更準(zhǔn)確反映一顆衛(wèi)星與其它可見星的冗余信息，將這個(gè)星與其它所有可見星的成本函數(shù)值總和作為其總成本值，關(guān)系為

(7)

衛(wèi)星的成本函數(shù)值越大，冗余信息也就越多。

通過分析及文獻(xiàn)[13]指出，次優(yōu)選星算法中，GDOP值變化曲線波動(dòng)較大，不穩(wěn)定，易發(fā)生跳變；在某些時(shí)刻GDOP值跳動(dòng)很大，出現(xiàn)峰值現(xiàn)象，如圖3所示。

圖3 次優(yōu)選星算法GDOP值峰值曲線

通過對峰值點(diǎn)對應(yīng)選出的衛(wèi)星及算法分析發(fā)現(xiàn)，一是次優(yōu)選星算法選取的衛(wèi)星集合中缺少高度角的衛(wèi)星，從成本函數(shù)也可推算知，衛(wèi)星高度角越大的衛(wèi)星成本函數(shù)值越大，選星過程中越易被排除；二是次優(yōu)選星算法選星過程僅根據(jù)衛(wèi)星成本函數(shù)，以剔除與其它可見星分布結(jié)構(gòu)較差的衛(wèi)星，而未考慮不同導(dǎo)航系統(tǒng)中衛(wèi)星信號、測量誤差的差異，以致選星結(jié)果較差；三是通過再添加篩選排除集合中的衛(wèi)星，對次優(yōu)選星算法進(jìn)行分步，選星結(jié)果和峰值現(xiàn)象能得到較大提高和改善。

因此，本文通過對次優(yōu)選星采用的成本函數(shù)進(jìn)行加權(quán)處理，即乘以權(quán)因子W，采用加權(quán)成本函數(shù)模型

(8)

2.2 權(quán)函數(shù)模型

對于組合系統(tǒng)，由于各衛(wèi)星系統(tǒng)不同衛(wèi)星發(fā)射的信號質(zhì)量、傳播路徑不同，相應(yīng)的偽距測量精度也不相同，主要與衛(wèi)星星鐘、大氣延遲、用戶設(shè)備和環(huán)境等相關(guān)。大氣延遲誤差與衛(wèi)星高度角相關(guān)，隨高度角的增大而減小；同時(shí)，高度角低的衛(wèi)星信號質(zhì)量通常差于高度角高的，低高度角的衛(wèi)星信號也更容易引起多路徑效應(yīng)。因此，常利用衛(wèi)星高度角建立隨機(jī)模型。但是由于高度角隨機(jī)模型為純粹的高度角數(shù)學(xué)函數(shù)表達(dá)，沒有考慮環(huán)境以及接收機(jī)本身的影響以及多路徑效應(yīng)的復(fù)雜性，僅利用高度角定權(quán)的效果不是很顯著[14]。而信噪比能夠有效反映衛(wèi)星觀測信號的質(zhì)量，是基本的導(dǎo)航信號質(zhì)量參數(shù)，常用載噪比定量表示。特別當(dāng)信號發(fā)生衍射時(shí)，信噪比相對高度角更能準(zhǔn)確反映用戶接收到的衛(wèi)星信號質(zhì)量。因此，可以看出單一以高度角或載噪比定權(quán)的方式，并不適應(yīng)于導(dǎo)航定位復(fù)雜多變的應(yīng)用環(huán)境。

此外，根據(jù)選星的原則：選取衛(wèi)星幾何構(gòu)型較好的衛(wèi)星集合，即選取高度角趨于最低或最高的衛(wèi)星。而高度分布同區(qū)域的衛(wèi)星，高度角差異小，定權(quán)效果相當(dāng)，不易篩選，而結(jié)合信噪比定權(quán)效果可知，更能反映細(xì)微差異；信噪比一定時(shí)，結(jié)合高度角定權(quán)能確保衛(wèi)星幾何分布。因此，提出以高度角el和載噪比C/N0聯(lián)合構(gòu)建的權(quán)函數(shù)模型

(9)

采用式(9)構(gòu)建的加權(quán)成本函數(shù)，也說明衛(wèi)星高度角越高、載噪比越高的衛(wèi)星加權(quán)成本函數(shù)越小，越不易被排除，也印證了成本函數(shù)選星理論。

2.3 分步次優(yōu)加權(quán)選星算法

通過前2節(jié)分析得到改進(jìn)的次優(yōu)選星算法，選星過程如下：

1)某一觀測歷元可見星數(shù)n顆(截止高度角15°，非開闊應(yīng)用環(huán)境，如遮擋、城市和峽谷等)，選星數(shù)m；

4)重復(fù)步驟2)和步驟3)，并根據(jù)選星數(shù)和組合導(dǎo)航系統(tǒng)個(gè)數(shù)確定的對應(yīng)高度角最少衛(wèi)星數(shù)4顆以及大量實(shí)驗(yàn)驗(yàn)證分析，得到直至剩余衛(wèi)星數(shù)為m-4；

5)在被排除的衛(wèi)星集合中依次選取一顆衛(wèi)星，結(jié)合已選衛(wèi)星，計(jì)算所有衛(wèi)星組合GDOP值，選取最小GDOP值的衛(wèi)星組合，共循環(huán)4次，即為最終選星結(jié)果。

針對GDOP值的循環(huán)計(jì)算過程，涉及矩陣的求逆，本文運(yùn)用矩陣求逆引理，不需重復(fù)計(jì)算高階矩陣的逆矩陣，每次計(jì)算僅通過循環(huán)使用上次結(jié)果，即可求得高階矩陣的逆，可大大降低運(yùn)算量，提高實(shí)時(shí)性。具體計(jì)算過程如下[15]：

式中：Aj表示觀測向量；i取值取決于衛(wèi)星系統(tǒng)，見式(3)陣A；Qn-1,j表示除第j顆衛(wèi)星，前n-1顆衛(wèi)星求得的未知參數(shù)的協(xié)方差陣；Qn和GDOPn表示n顆衛(wèi)星求得的未知參數(shù)的協(xié)方差陣和最小GDOP值。

3 實(shí)驗(yàn)分析

實(shí)驗(yàn)數(shù)據(jù)采用與我國區(qū)域星座分布近似的澳大利亞的IGS臺(tái)站nnor站(116.1927°E,-31.048 7°S,234.984 m H)2015年第343 d 08:00:00～23:23:30的數(shù)據(jù)，共1 920個(gè)歷元，與仿真實(shí)驗(yàn)采用的武漢站(114.357 3°E,30.5317°N,25.8 m H)的位置相對赤道近似南北顛倒。因此，兩臺(tái)站觀測到的衛(wèi)星星座空間分布近似一致，實(shí)驗(yàn)結(jié)果可相互驗(yàn)證說明。

通過實(shí)驗(yàn)結(jié)果對比分析最佳選星數(shù)為13顆時(shí)，最優(yōu)選星算法、次優(yōu)選星算法和分步次優(yōu)加權(quán)選星算法GDOP值以及兩種次優(yōu)算法相對最優(yōu)選星算法的GDOP差值△GDOP值，如圖4、圖5所示。

圖4 3種選星算法的GDOP值變化曲線

圖5 次優(yōu)、分步次優(yōu)加權(quán)選星算法與最優(yōu)選星算法的△GDOP值

從圖4、圖5可知，分布加權(quán)次優(yōu)選星算法GDOP值在1.5～2.5之間，與最優(yōu)選星算法的GDOP差值△GDOP維持在0.3左右，最小值為0，最大值約為0.8，說明其選星結(jié)果可能最大接近于最優(yōu)選星算法；相對次優(yōu)選星算法，GDOP值縮小一半，其變化幅度更小，曲線也相對平穩(wěn)、無峰值點(diǎn)，充分證明分步次優(yōu)加權(quán)選星算法優(yōu)于次優(yōu)選星算法，其選星結(jié)果更可靠。同時(shí)，統(tǒng)計(jì)3種選星算法GDOP的最大值、最小值、平均值，如表2所示。

表2 3種選星算法GDOP值

為進(jìn)一步分析選星算法與最優(yōu)算法的接近程度，可通過GDOP比值ζ評估[14]，其定義為

(10)

由于最優(yōu)選星算法選出的衛(wèi)星組合空間幾何構(gòu)型最好，其GDOP值自然就最小，因此ζ≥1。ζ越接近于1，說明選星算法的結(jié)果越符合于最優(yōu)選星結(jié)果，算法性能也就越好；ζ越大，算法效果就越差，結(jié)果就越不可靠。

統(tǒng)計(jì)比較分步次優(yōu)加權(quán)選星算法、次優(yōu)選星算法相對最優(yōu)選星算法的GDOP比值ζ的大小及共計(jì)1920個(gè)歷元對應(yīng)分布的每個(gè)ζ值區(qū)間的個(gè)數(shù)，分步如圖6所示。

圖6 兩種選星算法ζ分步

從圖6可看出，分步次優(yōu)選星算法ζ最小為1，最大為1.6，絕大部分值小于1.2，超過歷元總數(shù)的70%；而次優(yōu)選星算法ζ在1.2～2.8之間，均值在1.7附近，多半以上歷元數(shù)都位于均值區(qū)間。更進(jìn)一步證明上述觀點(diǎn)，分步次優(yōu)選星算法選星效果優(yōu)于次優(yōu)選星算法，結(jié)果更接近于最優(yōu)選星算法。

關(guān)于選星算法的實(shí)時(shí)性效果，可通過導(dǎo)航定位解算的計(jì)算量反映，主要在于選星過程的循環(huán)迭代次數(shù)、矩陣計(jì)算。矩陣計(jì)算快慢主要取決于矩陣維數(shù)的高低和求逆次數(shù)。以此次試驗(yàn)為例，觀測時(shí)段內(nèi)可見星平均數(shù)為23顆，選星數(shù)為13顆，4種選星算法計(jì)算GDOP值涉及的矩陣相乘的維數(shù)和求逆計(jì)算次數(shù)如表3所示。

表3 4種選星算法的運(yùn)算量

從表3可知，全視野法和次優(yōu)選星算法計(jì)算次數(shù)最少，1次。但全視野法，組合系統(tǒng)衛(wèi)星將達(dá)幾十顆甚至上百顆，矩陣A的維數(shù)隨之增長，計(jì)算量巨大；而次優(yōu)選星算法其選星結(jié)果GDOP值較大，可靠性較低，不宜應(yīng)用；分步次優(yōu)加權(quán)選星算法計(jì)算量相對較小，僅涉及第一步求兩兩衛(wèi)星方向向量間的夾角，23×3維的高階矩陣計(jì)算，后4顆衛(wèi)星選取只是循環(huán)次數(shù)較多，但每次僅是低維向量1×6維或6×1維計(jì)算，增加量相對最優(yōu)選星算法，矩陣求逆1 144 066次，計(jì)算量大大減少，且其選星結(jié)果也接近于最優(yōu)選星算法，更可靠。除此，分步次優(yōu)加權(quán)選星算法可隨用戶對精度的要求，隨時(shí)改變選星數(shù)，而計(jì)算過程只是第一步求逆矩陣的維數(shù)變化，相對原過程以及其他選星算法，計(jì)算量及增量仍較少，不影響實(shí)時(shí)性。因此，分步次優(yōu)加權(quán)選星算法可滿足導(dǎo)航系統(tǒng)精度和實(shí)時(shí)性要求。

4 結(jié) 論

本文首先通過STK仿真分析了中國區(qū)域GDOP值與衛(wèi)星數(shù)的關(guān)系，得出GPS，GLONASS，BDS組合導(dǎo)航系統(tǒng)在可見星較多時(shí)，最佳的選星數(shù)為13～17顆，并提出基于次優(yōu)選星算法的分步次優(yōu)加權(quán)選星算法，是根據(jù)衛(wèi)星在空間的幾何分布，利用衛(wèi)星的加權(quán)成本函數(shù)，選擇兩兩衛(wèi)星間夾角較大的衛(wèi)星集合。該算法相對次優(yōu)選星算法峰值和可靠性低的問題，有以下改進(jìn)：

1)針對組合系統(tǒng)的各衛(wèi)星的偽距測量誤差精度不同，采用衛(wèi)星的高度角與信噪比確定權(quán)函數(shù)，對衛(wèi)星成本函數(shù)進(jìn)行加權(quán)處理，即采用加權(quán)成本函數(shù)選星；

2)針對高度角的衛(wèi)星成本函數(shù)較大，易被排除的問題，可通過再分步選擇優(yōu)化，即在利用加權(quán)成本函數(shù)排除的衛(wèi)星集合中再選擇幾顆衛(wèi)星，根據(jù)最小GDOP值選取；

關(guān)于常規(guī)選星算法涉及高階矩陣、循環(huán)迭代等運(yùn)算問題，計(jì)算量十分巨大，耗時(shí)長、實(shí)時(shí)性差，而該選星算法運(yùn)用矩陣求逆引理，采用循環(huán)遞推，避免大量高階矩陣的運(yùn)算，提高解算速率，實(shí)時(shí)性較好。

[1] 叢麗，談?wù)怪? 提高衛(wèi)星導(dǎo)航定位精度和實(shí)時(shí)性的選星算法[J]. 系統(tǒng)工程與電子技術(shù), 2008, 30(10):1914-1917.

[2] MILLIKEN R J,ZOLLER C J. Principle of operation of NAVSTAR and characteristics[J]. Navigation,1978,25(2):96-106.

[3] 張貴明，黃順吉. 一種新的GPS導(dǎo)航衛(wèi)星選擇算法[J]. 電子科技大學(xué)學(xué)報(bào),2009,29(3):221-224.

[4] 陳浩，范勝林，劉建業(yè). GPS/Galileo組合導(dǎo)航定位系統(tǒng)中的選星算法[J]. 彈箭與制導(dǎo)報(bào)學(xué)報(bào),2009,29(4).

[5] ZU Miaoyan, JUN Z.A Fast Satellite Selection Algorithm: Beyond Four Satellites[J].Selected Topics in Signal Processing, IEEE Journal,2009,3(5): 740-747.

[6] ANHONG T. A new satellite selection algorithm in GNSS[C]. Information Management, Innovation Management and Industrial Engineering (ICIII), 2013 6th International Conference,2013.

[7] 吳瑞祥，蔡體菁. 基于高度角和方位角的選星方法[J]. 艦船電子工程, 2009, 29(11): 73-75.

[8] ZHANG L, DENG Z, YANG L. An improved satellite selection algorithm based on fuzzy comprehensive evaluation method and the entropy method for determining the weight of evaluation indicators[C]. Broadband Network and Multimedia Technology (IC-BNMT), 2011 4th IEEE International Conference on. IEEE, 2011:652-655.

[9] 張強(qiáng)，張曉林，李宏偉,等. 組合衛(wèi)星接收機(jī)中的選星算法[J]. 北京航空航天大學(xué)學(xué)報(bào)，2007，33(12):1424-1427.

[10] 金玲, 黃智剛, 李銳,等. 多衛(wèi)導(dǎo)組合系統(tǒng)的快速選星算法研究[J]. 電子學(xué)報(bào),2009, 37(9):1931-1936.

[11] 楊迪. GNSS多星座組合導(dǎo)航關(guān)鍵技術(shù)研究[D]. 南京：南京航空航天大學(xué), 2012.

[12] CHAN-WOO P, HOW J P.Quasi-optimal Satellite Selection Algorithm for Real-time Applications1[C].Proceedings of the 14th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 2001), Salt Lake City, UT, September,2001:3018-3028.

[13] WEI M. An improved satellite selection algorithm. Signal Processing (ICSP), 2012 IEEE 11th International Conference,2012.

[14] 張小紅, 丁樂樂. 北斗二代觀測值質(zhì)量分析及隨機(jī)模型精化[J]. 武漢大學(xué)學(xué)報(bào)(信息科學(xué)版), 2013,38(7):832-836.

[15] PHATAK M S. Recursive method for optimum GPS satellite selection[J]. Aerospace & Electronic Systems IEEE Transactions on, 2001, 37(2):751-754.

An improved satellite selection algorithm for integrated navigation system

FENG Biao, CHAI Hongzhou, PAN Zongpeng, WANG Min, YANG Kefan

(Information Engineering University, Zhengzhou 45000, China)

This paper analyzes the selection of satellites for GPS, GLONASS and BDS integrated navigation system. Firstly, the relationship between the geometric dilution of precision GDOP and the number of satellites is analyzed with STK simulation to obtain the best SVs selection. Secondly, according to the spatial distribution of satellite constellation, based on the cost function of quasi-optimal satellite selection algorithm, and combined with the difference in measurement precision of satellites for integrated satellite system, the peak value and unstable characteristics of quasi-optimal satellite selection algorithm, a weighted cost function model is built determined by the satellite elevation angle and signal to noise ratio. And a step-by-step quasi-optimal weighted satellite selection algorithm is proposed based on the weighted cost function. Experimental result shows that the proposed algorithm can approximate the effect of the optimal selection algorithm, and the computational load is relatively small, which can satisfy the accuracy and real-time requirements of navigation and positioning solution.

integrated navigation system; STK; GDOP; weighted cost function model; step-by-step quasi-optimal weighted satellite selection algorithm

2016-11-14

國家自然科學(xué)基金資助項(xiàng)目(41574010;41274045)

馮 彪(1990-)，男，碩士研究生.

著錄：馮彪，柴洪洲，潘宗鵬，等.一種改進(jìn)的組合導(dǎo)航系統(tǒng)選星算法[J].測繪工程，2018，27(2)：26-31.

10.19349/j.cnki.issn1006-7949.2018.02.005

P228.4

A

1006-7949(2018)02-0026-06

張德福]