深水立管柔性接頭橡膠-鋼粘結界面端應力場分析
,,,
(1.深水油氣管線關鍵技術與裝備北京市重點實驗室,北京 102617;2.北京石油化工學院機械工程學院,北京 102617;3.湖北海洋工程裝備研究院有限公司,武漢 430064)
深水立管柔性接頭橡膠-鋼粘結界面端應力場分析
陳景皓1,2,葉茂3,鄧博松2,侯廣成1,2
(1.深水油氣管線關鍵技術與裝備北京市重點實驗室,北京 102617;2.北京石油化工學院機械工程學院,北京 102617;3.湖北海洋工程裝備研究院有限公司,武漢 430064)
彈性體為深水立管柔性接頭關鍵部件,與主體結構粘結的界面端附近為易發生損傷部位,針對其破壞機理問題,采用有限元軟件ABAQUS對橡膠-鋼粘結界面端的應力場及其影響因素進行分析,結果表明:橡膠-鋼粘結界面端附近應力場存在明顯的應力集中現象,并在θ=60°這一路徑上的應力最大;改變界面端結合角可以影響橡膠-鋼粘結界面端應力大小,但影響很小。
深水立管;柔性接頭;橡膠-鋼;界面端;應力場
深水立管柔性接頭關鍵部件彈性體是主要承力結構,為橡膠鋼復合結構。其中,彈性體中的橡膠材料與主體粘結在一起,如圖1所示。由于在雙材料粘結界面兩端的力學屬性不同而產生力學參數上的不連續,使得結合材料在橡膠-鋼粘結界面端附近產生應力集中(如圖1編號為1、2、3、4點處),結構破壞大多從這些地方開始。

圖1 深水立管柔性接頭內部結構
雙材料粘結界面端的研究主要集中在如何求解界面端應力場的問題上。對于結構、材料性能、受力形式比較簡單的情況,國內外學者分別采用不同的理論求得雙材料界面端應力場的解[1-6]。深水立管柔性接頭彈性體這種含有橡膠超彈性材料的結構,采用理論的方法無法得到精確解。面對這種情況,采用有限單元法對雙材料界面端應力場進行分析被認為是一種有效的方式[7-10]。因此,為進一步研究橡膠-鋼粘結界面端的結構破壞機理,考慮采用有限元軟件ABAQUS并結合描述橡膠超彈性本構關系的Mooney-Rivlin模型對橡膠-鋼粘結界面端應力場進行分析,并對影響橡膠-鋼粘結界面端應力場的因素進行參數分析。
1 橡膠-鋼粘結界面端有限元模型
1.1 幾何模型
為研究橡膠-鋼粘結界面端附近應力場,以及界面端結合角對橡膠-鋼粘結界面端附近應力分布的影響,建立如圖2所示幾何模型。橡膠與鋼2種材料表面粘結在一起,忽略粘結層的厚度,假設粘結層為理想界面。橡膠與鋼均確定為平板形狀,其中,中間部分為橡膠,上下部分為鋼。圖2中,θ和α分別為橡膠和鋼界面端的幾何形狀角,α取值180°,θ取值為90°。
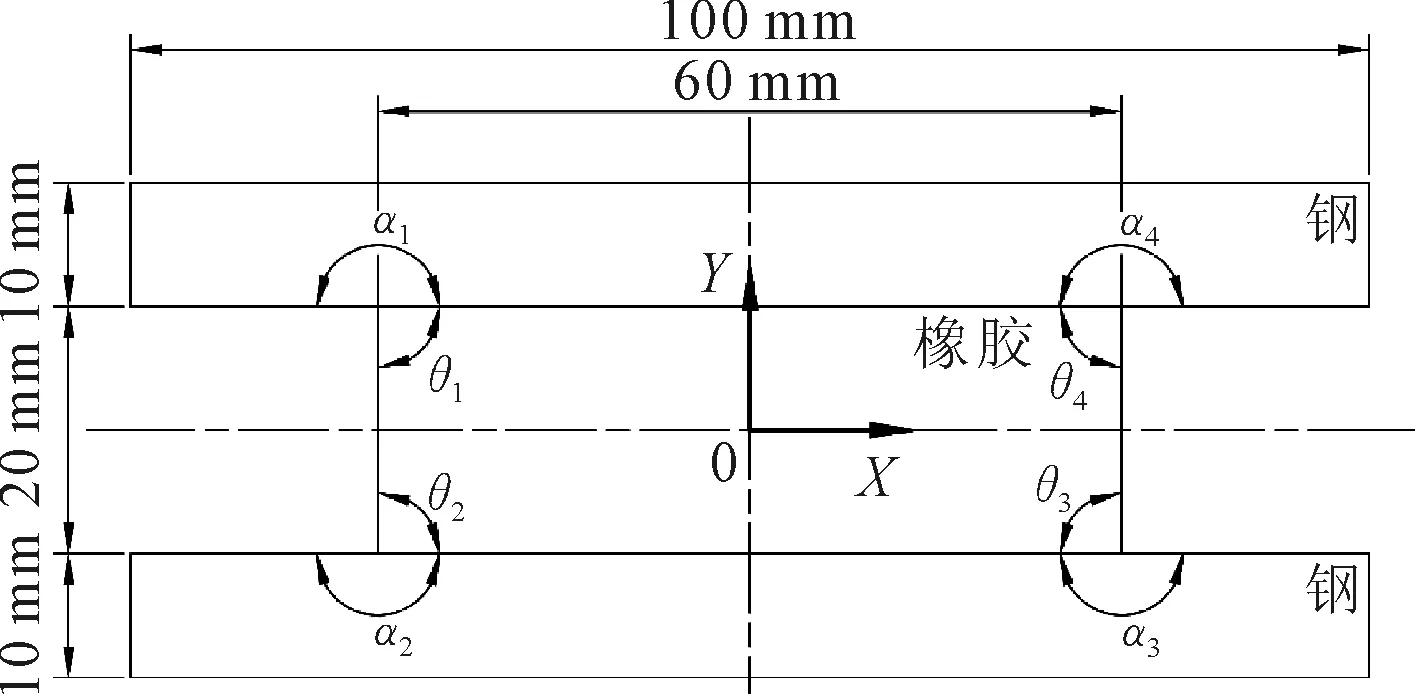
圖2 橡膠-鋼粘結界面端有限元模型幾何尺寸
1.2 材料屬性定義
鋼彈性模量為208 GPa,泊松比為0.3。橡膠為超彈性材料,大變形的條件下,不能簡單地以彈性模量來描述。描述橡膠超彈性本構關系的模型,如Mooney-Rivlin模型、Ogden模型、Neo-Hookean模型[11]。選擇2參數Mooney-Rivlin模型。
W=C1(I1-3)+C2(I2-3)
(1)
式中:W為應變能函數;I1和I2分別是第一、第二應變不變量;C1和C2為常數,分別取0.390 MPa和0.344 MPa。
1.3 邊界條件與載荷定義
為了模擬橡膠-鋼粘結界面端受壓與受剪狀態,分別在上端鋼的頂部與左側加載均勻分布的位移邊界條件,大小為2 mm,并在下端鋼的底部設定為固定邊界條件。
1.4 網格劃分
橡膠和鋼均采用CPS4R模擬,為捕捉橡膠-鋼粘結界面端附近應力變化情況,在以界面端為圓心,2 mm為半徑的區域對橡膠和鋼均進行網格細化,見圖3。
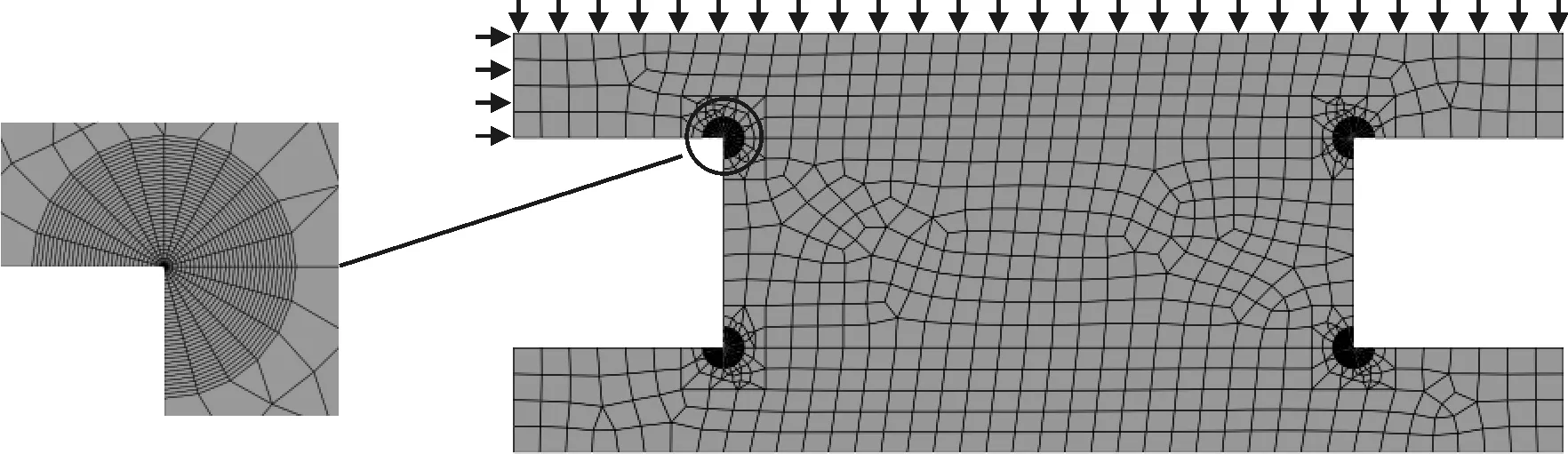
圖3 橡膠-鋼粘結界面端有限元模型網格劃分
2 應力場
由于彈性體的破壞都是發生在橡膠材料部分,故重點分析橡膠-鋼粘結界面端附近橡膠材料部分的應力場。按照極坐標的形式提取橡膠界面端附近應力場見圖4。
由于受壓狀態下模型的幾何形狀與受力狀態關于OY軸對稱,只需分析界面端1和界面端2附近的應力場。受壓狀態和受剪狀態下橡膠界面端的應力場分別見圖5、6。
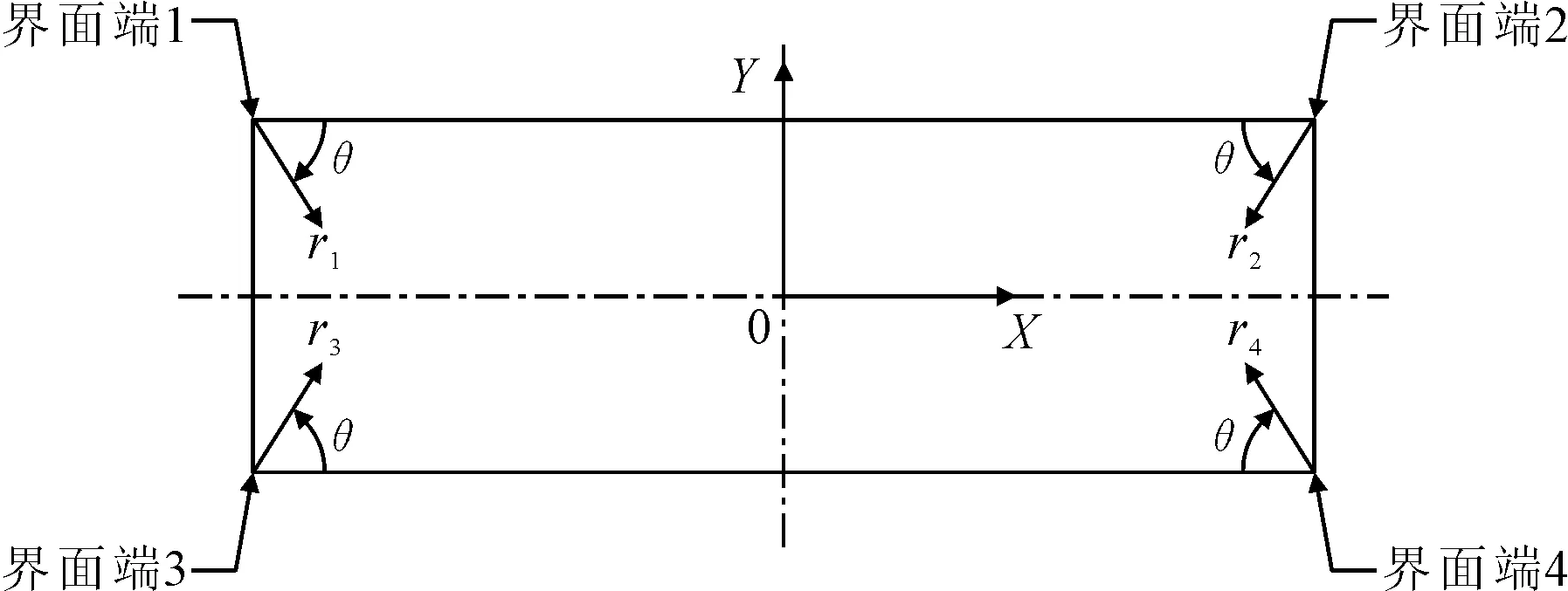
圖4 橡膠材料界面端附近應力場及坐標定義
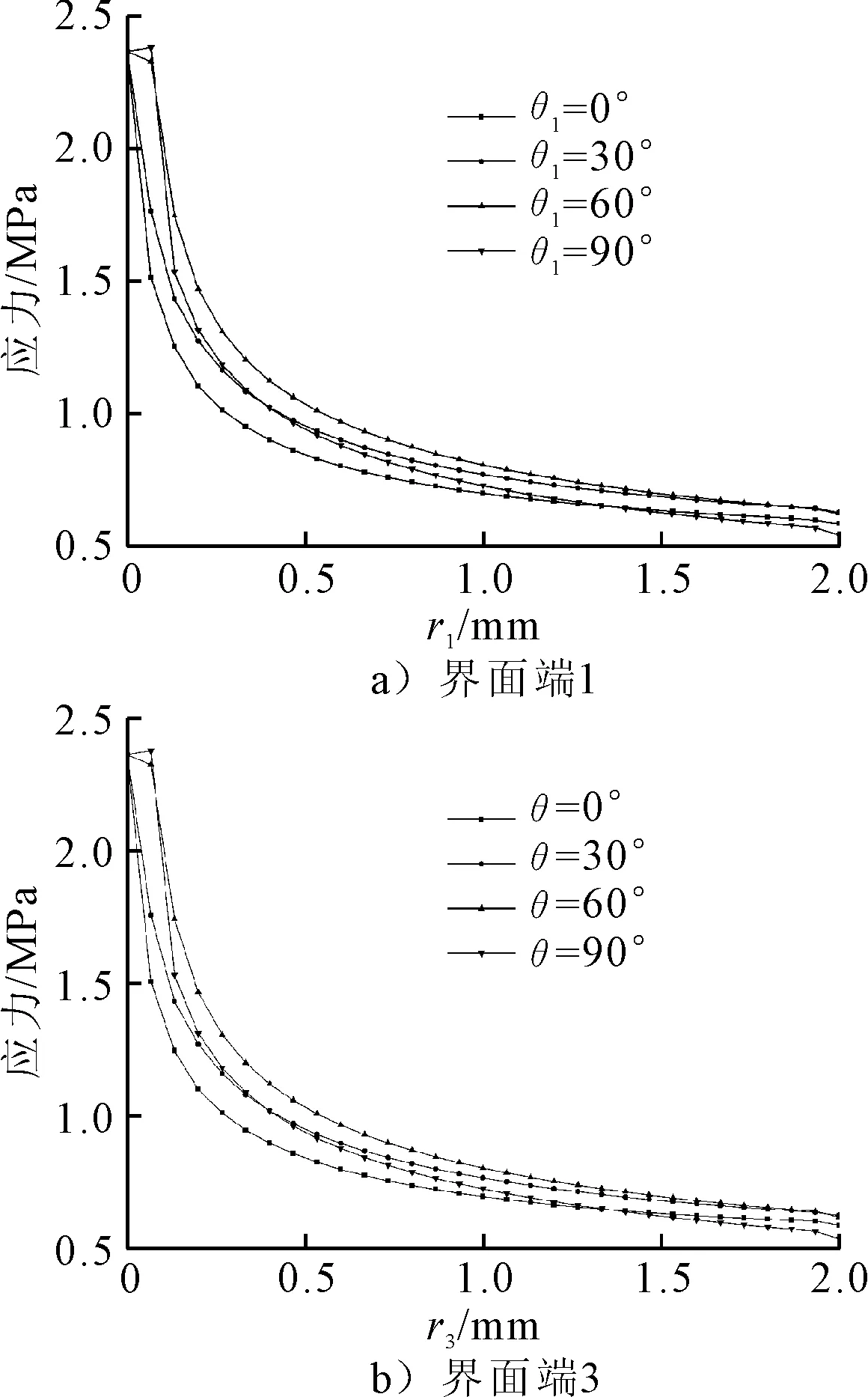
圖5 受壓狀態下橡膠界面端應力場

圖6 受剪狀態下橡膠界面端應力場
由圖5、6可見,2種受力狀態下橡膠界面端處的應力相對最大,并隨著r值的增加而減小。圖5表明,界面端1與界面端3的最大應力出現在θ=90°,r=0.066 7 mm處,約為2.38 MPa。相比較在θ=90°,r=2 mm處應力最小,約為0.538 MPa。圖6表明,4個界面端的最大應力值均出現在r=0 mm,約為1.1 MPa。相比較,在r=2 mm處應力最小,約為0.27 MPa。對比θ=0°、30°、60°、90°這4條路徑上橡膠界面端附近的應力分布情況發現,在θ=60°這一路徑上,橡膠界面端附近的整體應力水平高于其他3條路徑。
3 橡膠-鋼粘結界面端應力場參數
前面的分析表明,在橡膠-鋼粘結界面端附近存在著明顯的應力集中現象,應盡量減小橡膠-鋼粘結界面端附近應力場的大小,以避免結構發生破壞。界面端結合角對于線彈性小變形雙材料粘結界面端附近應力場有一定影響[12-13]。為此,選擇鋼界面端角(即α角)為180°、150°、120°、90°時,橡膠界面端附近應力場的變化情況,并選擇θ=60°這一路徑進行對比。以鋼界面端角為180°為基準,分別用4種鋼界面端角對應的橡膠界面端應力與鋼界面端角為180°時橡膠界面端的應力相減,分析鋼界面端角對橡膠界面端附近應力場的影響。
從圖7可以看出,橡膠材料在受壓狀態下界面端1附近應力在鋼界面端角為90°時最大,界面端3附近應力在鋼界面端角為150°時最大,界面端1和界面端3附近應力在鋼界面端角為180°時最小。
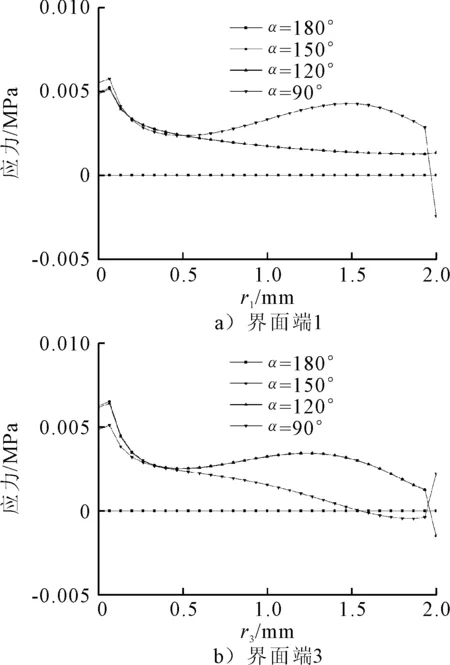
圖7 受壓狀態下橡膠界面端應力場隨界面端結合角的變化規律
從圖8可以看出,橡膠材料在受剪狀態下界面端1附近應力在鋼界面端角為90°時最大,180°時最小;界面端2附近應力在鋼界面端角為120°時最大,180°時最小;界面端3附近應力在鋼界面端角為180°時最大,90°時最小;界面端4附近應力在鋼界面端角為180°時最大,150°時最小。綜合以上分析表明,通過改變界面端結合角能夠改變橡膠-鋼粘結界面端附近的應力狀態,但變動幅值相對很小。
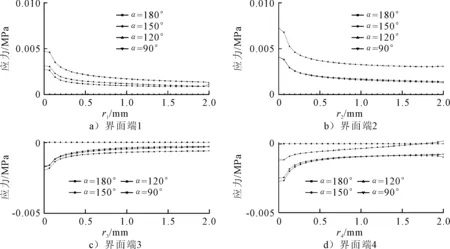
圖8 受剪狀態下橡膠界面端應力場隨界面端結合角的變化規律
4 結論
對深水立管柔性接頭橡膠-鋼粘結界面端附近的應力場有限元分析結果表明,在橡膠-鋼粘結界面附近存在明顯的應力集中現象,在柔性接頭的使用過程中應注意該區域的損傷情況。不同于線彈性小變形雙材料,通過改變界面端結合角來減小橡膠-鋼粘結界面端附近的應力收效甚微,應尋求其他方式。
[1] BOGY D B. On the problem of edge bonded elastic quarter-planes loaded at the boundary[J]. International journal of Solids and structures,1970,6(9):1287-1313.
[2] SATOR C, BECKER W. Closed-form solutions for stress singularities at plane bi- and trimaterial junctions[J]. Archive of applied mechanics,2012,82(5):643-658.
[3] MUNZ D, FETT T, YANG Y Y. The regular stress term in bonded dissimilar materials after a change in temperature[J]. Engineering fracture mechanics,1993,44(2):185-194.
[4] YANG Y Y, MUNZ D, Stress singularities in a dissimilar materials joint with edge tractions under mechanical and thermal loadings[J]. International journal of solids and strucrures,1997,34(10):1199-1216.
[5] 戴瑛,嵇醒.界面端應力奇異性及界面應力分布規律研究[J].中國科學G輯:物理學力學天文學,2007,37(4):535-543.
[6] 安春利,任全彬,王鐵軍,等.柔性接頭界面端角點應力奇異性[J].固體火箭技術,2012,35(3):391-395.
[7] ZHANG Y, NODA N A, LAN X, et al. Stress intensity factors of a crack on the interface of adhesive and adherents[J]. Key engineering materials,2010,(452/453):249-252.
[8] ZHAN Y, NODA N A, TAKAISI K, et al. Effect of adhesive thickness on the intensity of singular stress at the adhesive dissimilar joint[J]. Journal of solid mechanics and materials engineering,2010,4(10):1467-1479.
[9] MONCHAI P. HIDEO K. Stress singularity analysis around the singular point on the stress singularity line in three-dimensional joints[J]. International journal of solids and structures,2005,42(11-12):3059-3074.
[10] PAGEAU S S, BIGGERS S B. A finite element approach to three-dimensional singular stress states in anisotropic multi-material wedges and junctions[J]. International journal of solids and structures,1996,33(1):33-47.
[11] 徐立,吳桂忠.有限元分析中橡膠應變能函數的若干形式[J].橡膠工業,1999,46(12):707-711.
[12] 吳志學.雙材料界面端附近奇異應力場消除幾何條件研究[J].工程力學,2004,21(6):193-196.
[13] 秦曉東.平面塔接結構界面的應力分析[D].沈陽:東北大學,2010.
Stress Field Analysis of Rubber-steel Bonded Interface Corner of Deepwater Riser Flex-joint
CHENJing-hao1,2,YEMao3,DENGBo-song2,HOUGuang-cheng1,2
(1.Beijing Key Laboratory of Pipeline Critical Technology and Equipment for Deepwater Oil & Gas Development, Beijing 102617, China;2.School of Mechanical Engineering, Beijing Institute of Petrochemical Technology, Beijing 102617, China;3.Chinese Institute of Marine & Offshore Engineering (HB) Co. Ltd., Wuhan 430064, China)
Elastomer is the key component of the flex-joint of deep-water riser, which is bonded with major structure. The bonded interface corner of these two components is liable to be damaged. In order to investigate the failure mechanism, finite element software ABAQUS was used to analysis stress field of rubber-steel bonded interface corner and its influencing factor. The results showed that stress field of rubber-steel bonded interface corner would form stress concentration and the maximum stress is at the path of. The change of interface bounded angle would affect the stress magnitude of rubber-steel bonded interface corner, but this effect is small.
deepwater riser; flex-joint; rubber-steel; interface corner; stress field
P754
A
1671-7953(2017)06-0182-04
10.3963/j.issn.1671-7953.2017.06.041
2017-02-22
2017-03-27
北京市教委科研項目(KM201610017002)
陳景皓(1983—),男,博士,講師
研究方向:立管疲勞與斷裂

