在風浪影響下的集裝箱船航速分析

魏照坤+謝新連+魏明+包甜甜

摘要：為優化集裝箱船航速，減少油耗，在考慮風浪干擾的基礎上，根據船舶航行中的功率關系，建立船舶減速模型。該模型能夠計算出在不同風浪條件下船體所受風、浪干擾力以及船舶減速幅度。將建立的減速模型與現有的擬合模型進行對比，結果表明，來自船舶正橫前和正橫后的風浪合力對船舶航行起到阻礙作用。當風浪來自船舶正橫前時船舶降速的幅度較大；當風浪來自船舶正橫后時船舶降速幅度較小；船舶降速幅度在相同風浪條件下會隨著航速的增大而減小。建立的減速模型比擬合模型更具有適用性，利用建立的模型能夠較為準確地估算出在風浪影響下船舶的減速幅度。

關鍵詞： 交通工程； 降速分析； 功率模型； 集裝箱船； 風浪

中圖分類號： U674.131；U692.33 文獻標志碼： A

Abstract： To optimize the speed of container ships so as to reduce fuel consumption， considering the disturbance of wind and wave， a model for determining reduced speed is designed according to the power relationship of underway ships. The wind and wave disturbance forces applied to the hull and the deceleration range of ships under different conditions of wind and wave can be obtained by the model. The model is compared with the existing fitting model， which shows that the resultant force of wind and wave from the forward of the beam and abaft the beam hinders the navigation of ships. The speed loss is larger when the wind and wave are from the forward of the beam； the speed loss is lower when the wind and wave are abaft the beam； in the same wind and wave condition， the speed loss becomes lower with the speed being up. The proposed model is more applicable than the fitting model. By the model， the reduced speed can be estimated accurately.

Key words： traffic engineering； speed loss analysis； power model； container ship； wind and wave

0 引 言

隨著全球航運的逐步回暖，以及人們環境保護意識的不斷增強，船舶油耗問題越來越受到學者們的關注。船舶油耗問題的研究離不開對船舶航速的分析。因此，分析風浪等外部條件對航速產生的影響，提高油耗優化的準確性顯得尤為重要。

當前，在航速和班輪服務優化研究中，對油耗成本的估算都淡化了外部氣象條件的影響。RONEN[1-3]鑒于油耗在船舶營運成本中占有較高的比例（約為20%～60%），為估算油耗成本，提出了每日油耗量正比于航速的三次方的估算模型，并利用該模型對集裝箱船的航速和船隊規模進行了優化；唐磊等[4]利用RONEN提出的模型，構建了基于時間窗的不定期船舶航速優化模型；WANG 等[5]利用不同載箱量的集裝箱船航速和油耗歷史數據，對二者的關系進行了擬合，得到了在不同載箱量下航速與油耗的具體函數表達式，并根據擬合結果對考慮轉運的班輪運輸網絡中的船舶航速進行了優化。此外，MENG等[6]、GELAREH 等[7-8]、SHINTANI等[9]在優化班輪服務時，采用將航速假設為定值的方法來估算油耗量。

綜上所述，現有的研究中主要利用航速進行油耗量估算，而都忽略了氣象條件對航速的影響，必然會影響優化結果和油耗量估算的準確性。因此，有效地量化風浪對船舶航速產生的影響，對優化船舶航速，提高油耗量估算的準確性具有重大意義。針對此問題，本文建立在風浪影響下的集裝箱船減速模型，分析風浪對船舶航速的不良影響并估算船舶減速幅度。

1 干擾力模型

在風浪中航行的船舶，由于受風浪的作用會產生搖蕩、甲板上浪等現象，船舶航速在推進功率不變的情況下比靜水中小。因此，為計算船舶減速幅度，需要對風浪干擾力進行建模。

1.1 風干擾力模型

在僅考慮船舶平面運動的情況下，風作用在船體上層建筑上產生的流體動力具有艏艉方向和橫向的分量。鑒于船舶在航行中的前進速度遠大于橫向速度，在本文構建的模型中忽略船舶橫向分量，僅考慮艏艉方向上的分量。艏艉方向上的分量受相對風速、風舷角、風壓力系數及受風面積的影響，艏艉方向上的平均風壓力[10]為X=12ρaA1vw2Cx（α1）

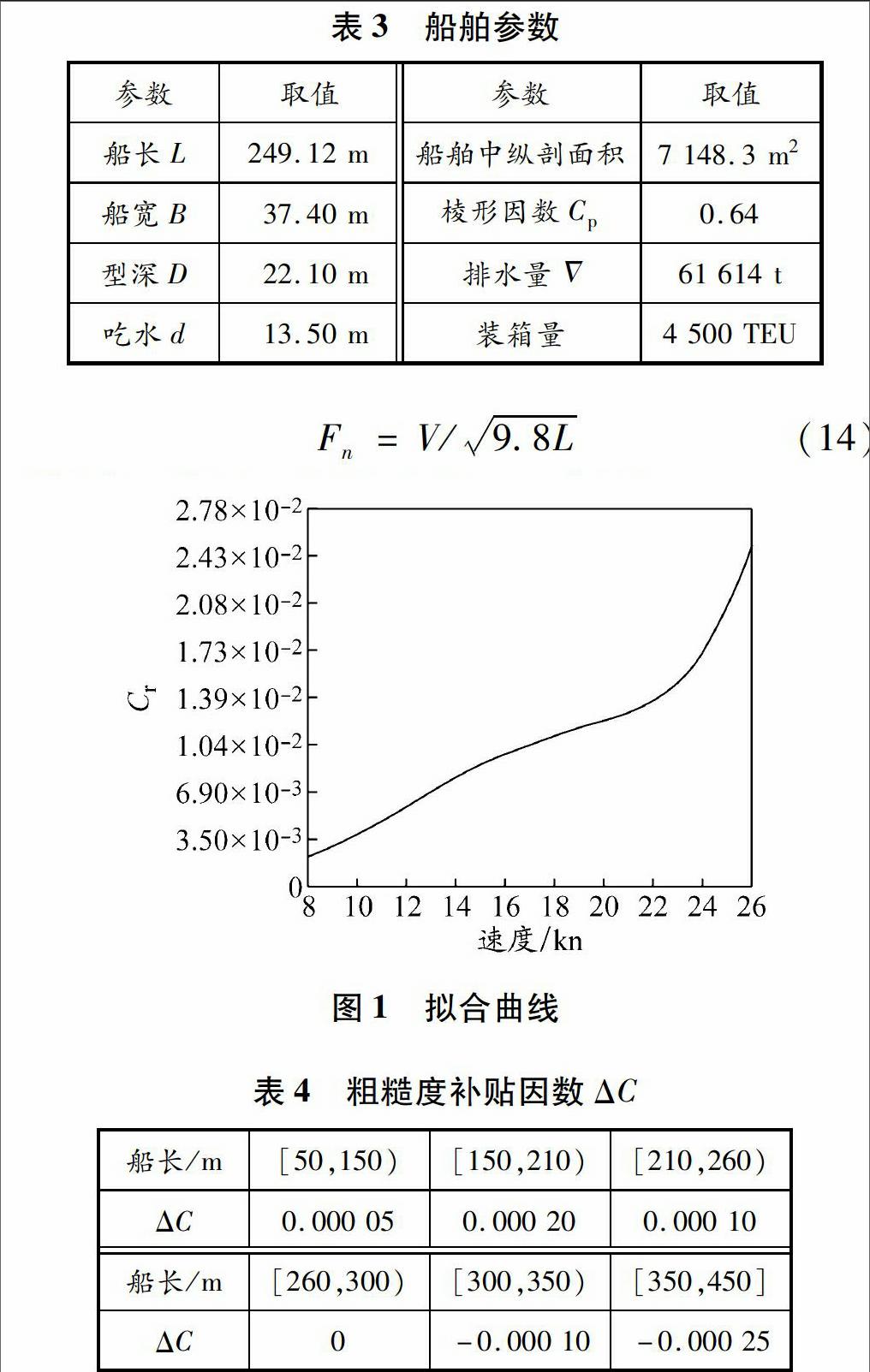
一般采用藍波-奧芬凱勒圖譜法計算非高速船舶Cr。為便于在模型求解中使用，需要對由船舶資料確定的圖譜曲線進行擬合。根據船舶資料確定的圖譜曲線為藍波-奧芬凱勒A圖譜中Cp為0.64的曲線，將Fn作為自變量，Cr作為因變量，利用最小二乘法對式（14）進行擬合，獲得圖1所示的擬合曲線。粗糙度補貼因數ΔC可以通過表4[18]獲得。endprint

3.2 干擾力分析

根據式（1）對不同風向和風速的干擾力進行計算，得到圖2a）。由圖2a）可以看出：當風來自船舶正橫前時，隨著風速的增大風干擾力相應增大，而當風速大小相同時，風干擾力隨著風的來向與船首夾角的增大而減小；當風來自船舶正橫后時，風干擾力的變化與風來自正橫前的情況相同，但當風速足夠大時，風干擾力會出現波動（如風速為15 m/s時的風干擾力曲線）。圖2b）是波浪干擾力示意圖。由圖2b）可知，艏艉方向上波浪干擾力隨著浪的來向與船首夾角的增大而減小，當接近正橫時達到最小，隨后干擾力的大小又隨著浪的來向與船首夾角的增大而增大。

3.3 船舶減速分析

根據式（9）和（11）可以計算在不同風速、風向、浪高（采用文獻[10]中的風速回歸公式計算，因此風速確定的情況下浪高確定）和浪向的情況下，利用功率模型和擬合模型分別得到的船舶航速，見圖3。這里，船舶在靜水中的航速為15 kn。

通過圖3可以發現，船舶減速的趨勢在兩個模型中是一致的，即隨著風浪來向與船首夾角的增大，船舶減速的幅度減小，當風浪來向與船首夾角在150°到180°之間時，風浪對船舶起到微小的推進作用。然而，船舶減速的幅度在兩個模型中不等。用兩個模型得到的在不同風浪條件下的船舶減速幅度見圖4。這里，船舶在靜水中的航速為15 kn。

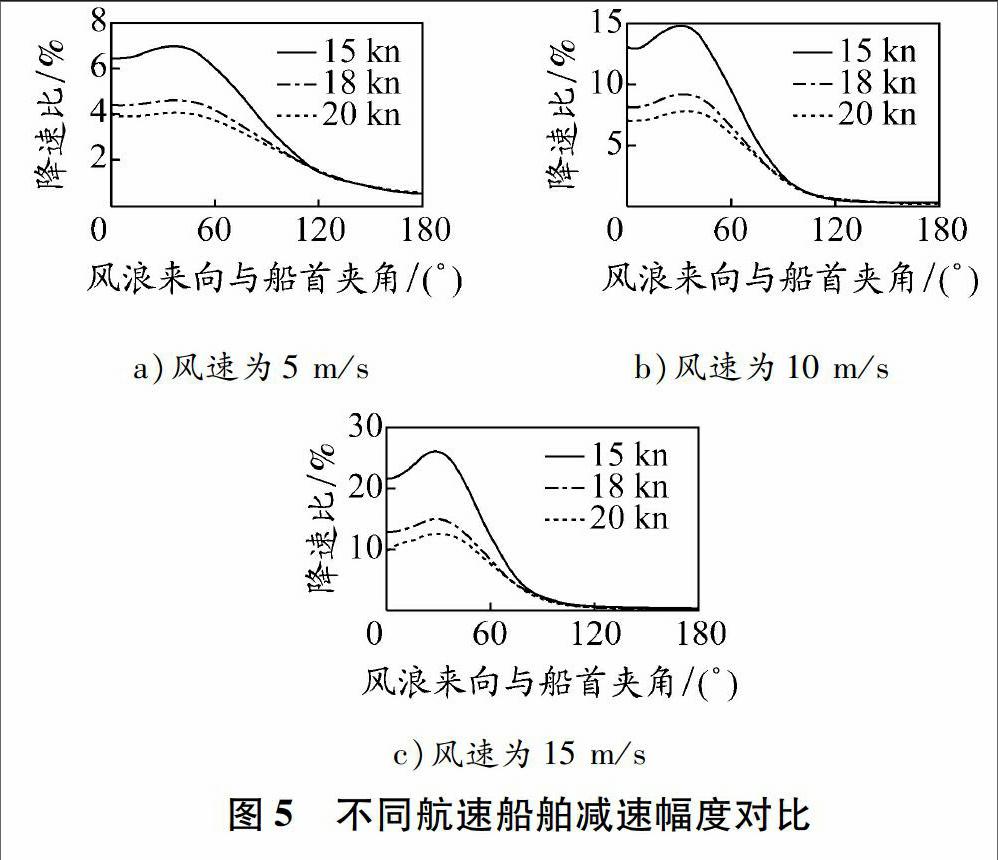
根據圖3和4可以發現，船舶的減速幅度隨著風浪來向與船首夾角的增大而減小。在風浪較小時，擬合模型中的船舶減速幅度比功率模型中的小；在風浪較大時，擬合模型中船舶減速幅度比功率模型中的大。然而，在擬合模型中船舶航速對風向的變化不敏感，其曲線呈階梯狀，不能實時反映風浪來向變化對船舶航速的影響。此外，通過試驗發現，船舶航速產生最大降幅并不是在完全頂風頂浪航行時，而是當風浪來向與船首成一定夾角時，且產生最大降幅時風浪來向與船首間的夾角會隨著航速的變化而改變。綜上所述，功率模型能夠較好地反映船舶航速受風浪影響而發生的變化，且航速下降的幅度也接近船舶實際運行的情況，因此該模型更具有適應性。為進一步分析風浪對船舶航速的影響，改變靜水中的船舶航速，觀測船舶在不同風浪條件下的減速幅度，見圖5。圖5表明，在相同的風浪條件下，隨著船舶航速的增加，船舶減速幅度會減小。

4 結 論

風浪會對船舶的速度產生較大的影響從而間接影響船舶油耗，因此對在風浪影響下船舶航速變化的分析有助于船舶駕駛員合理駕控船舶。基于此目的，本文建立了在風浪影響下的船舶減速功率模型。模型仿真結果表明，來自船舶正橫前和正橫后的風浪合力對船舶航行起到阻礙作用。當風浪來自船舶正橫前時，船舶降速的幅度較大，且風浪干擾力隨著風浪來向與船首夾角的增大而減小；當風浪來自船舶正橫后時，船舶降速幅度較小，風干擾力隨著風的來向與船首夾角的增大而減小，波浪干擾力則隨著波浪的來向與船首夾角的增大而增大，其方向也由艏向改為艉向。將構建的模型與現有的擬合模型進行對比，前者的仿真結果對于風浪等外部條件變化比較敏感，且較符合船舶運行的實際情況，可以有效估算船舶風浪中的減速，有助于合理構建船舶航速優化模型，因此更具有適用性和應用價值。然而，本文所構建的模型也存在一定的不足，主要體現在未能考慮在干擾力作用下耦合運動對航速產生的影響。因此，計算的結果與實際值之間必然存在著一定的誤差。今后的研究工作應從此方面入手，進一步考慮力矩的作用，提高減速幅度估算的準確性。

參考文獻：

[1] RONEN D. The effect of oil price on the optimal speed of ships[J]. Journal of the Operational Research Society， 1982， 33（11）： 1035-1040. DOI： 10.2307/2581518.

[2] RONEN D. Ship scheduling： the last decade[J]. European Journal of Operational Research， 1993， 71（3）： 325-333. DOI： 10.1016/0377-2217（93）90343-L.

[3] RONEN D. The effect of oil price on containership speed and fleet size[J]. Journal of the Operational Research Society， 2011， 62（1）： 211-216. DOI： 10.1057/jors.2009.169.

[4] 唐磊， 謝新連. 帶時間窗約束的不定期船航速優化模型[J]. 物流技術， 2014， 33（2）： 132-135. DOI： 10.3969/j.issn.1005-152X.2014.02.044

[5] WANG Shuaian， MENG Qiang. Sailing speed optimization for container ships in a liner shipping network[J]. Transportation Research Part E， 2012， 48： 701-714. DOI： 10.1016/j.tre.2011.12.003.

[6] MENG Qiang， WANG Shuaian. Optimal operating strategy for a long-haul liner service route[J]. European Journal of Operational Research， 2011， 215： 105-114. DOI： 10.1016/j.ejor.2011.05.057.endprint

[7] GELAREH S， PISINGER D. Fleet deployment， network design and hub location of liner shipping companies[J]. Transportation Research Part E， 2011， 47： 947-964. DOI： 10.1016/j.tre.2011.03.002.

[8] GELAREH S， NICKEL S， PISINGER D. Liner shipping hub network design in a competitive environment[J]. Transportation Research Part E， 2010， 46： 991-1004. DOI： 10.1016/j.tre.2010.05.005.

[9] SHINTANI K， IMAI A， NISHIMURA E， et al. The container shipping network design problem with empty container repositioning[J]. Transportation Research Part E， 2007， 43： 39-59. DOI： 10.1016/j.tre.2005.05.003.

[10] 賈欣樂， 楊鹽生. 船舶運動數學模型[M]. 大連： 大連海事大學出版社， 1999： 297-298.

[11] DAIDOLA J C， GRAHAM D A， CHANDRASH L. A simulation program for vessels manoeuvring at slow speed[C] //Proceeding of 11th ship Technology and Research symposium， 1986： 1-11.

[12] SEN D， PADHY C P. An approach for development of a ship routing algorithm for application in the North Indian Ocean region[J]. Applied Ocean Research， 2015， 50： 173-191. DOI： 10.1016/j.apor.2015.01.019.

[13] LIN Y H， FANG M C， YEUNG R W. The optimization of ship weather-routing algorithm based on the composite influence of multi-dynamic elements[J]. Applied Ocean Research， 2013， 43： 189-194. DOI： 10.1016/j.apor.2013.07.010.

[14] FANG M C， LIN Y H. The optimization of ship weather-routing algorithm based on composite influence of multi-dynamic elements （II）： optimized routings[J]. Applied Ocean Research， 2015， 50： 130-140. DOI： 10.1016/j.apor.2013.07.010.

[15] TOWNSIN R L， KWON Y J. Estimating the influence of weather on ship performance[C]//Proceedings of International Symposium on TransNav， 1993： 191-209.

[16] PARK J， KIM N. Two-phase approach to optimal weather routing using geometric programming[J]. Journal of Marine Science & Technology， 2015， 20： 100-110. DOI： 10.1007/s00773-015-0321-6.

[17] 孟曉東， 袁章新. 考慮不規則風浪影響的最小油耗航速模型[J]. 上海海事大學學報， 2016， 37（1）： 19-24. DOI： 10.13340 /j.jsmu.2016.01.004.

[18] 巖井聰. 操船論[M]. 北京： 人民交通出版社， 1984： 333-336.

（編輯 趙勉）endprint