直線方程中的對稱問題分類解析

■孫建國

直線方程中的對稱問題分類解析

■孫建國

解析幾何中的對稱問題是高考中的“常客”，破解這類問題的關鍵是利用轉化求解，即將點線位置關系問題轉化為方程問題求解。下面分類解析，供同學們參考。

一、點關于點的對稱問題

例 1 過點P（0，l）作直線l使它被直線ll：2x+y—8=0和l2：x—3y+l0=0截得的線段被點P平分，求直線l的方程。

解：設直線ll與l的交點為A（a，8—2a）。

由題意知，點A關于點P的對稱點B（—a，2a—6）在l2上，代入l2的方程得—a—3（2a—6）+l0=0，解得a=4，即得點A（4，0）在直線l上。

所以由兩點式可得直線l的方程為x+4y—4=0。

評注：若點 M（xl，yl）與N（x，y）關于點P（a，b）對稱，則點P是線段MN 的中點。

二、點關于直線的對稱問題

例 2 已知直線l：2x—3y+l=0，點A（—l，—2），求點A關于直線l的對稱點A′的坐標。

解：設A′（x，y）。

由已知條件可得方程組：

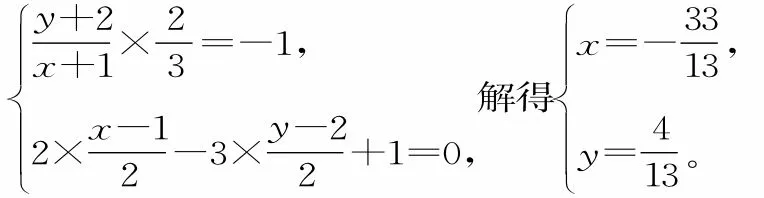
評注：若兩點 Pl（xl，yl）與 P2（x2，y2）關于直線l：Ax+By+C=0對稱，則線段PlP2的中點在對稱軸l上，且連接Pl，P2的直線垂直于對稱軸l。

三、直線關于直線的對稱問題

例 3 已知直線l：2x—3y+l=0，求直線m：3x—2y—6=0關于直線l的對稱直線m′的方程。

解：在直線m 上取一點，如 M（2，0），則點M（2，0）關于直線l的對稱點M′必在直線m′上。

設對稱點 M′（a，b）。

由題意可得方程組：

又直線m′經過點N（4，3），所以由兩點式得直線m′的方程為9x—46y+l02=0。

評注：對于此類問題，一般轉化為點關于直線的對稱問題來解決。

四、對稱問題的綜合應用

例 4 已知光線從點A（—4，—2）射出，到直線y=x上的點B后被直線y=x反射到y軸上的點C，又被y軸反射，這時反射光線恰好過點D（—l，6），求線段BC所在的直線方程。

解：作出簡圖，如圖l所示。

設點A關于直線y=x的對稱點為A′，點D關于y軸的對稱點 為 D′，則 易 得A′（—2，—4），D′（l，6）。由入射角等于反射角可知A′D′所在的直線經過點B與點C。

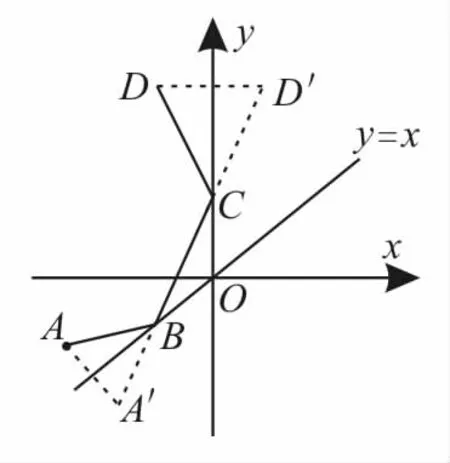
圖l

評注：物理中的光線反射問題，一般都可轉化為解析幾何中的對稱問題。解決中心對稱問題的關鍵在于運用中點坐標公式，而解決軸對稱問題，一般轉化為求對稱點的問題。

江蘇太倉高級中學

（責任編輯 郭正華）