液壓傳動型風力發(fā)電機組恒轉(zhuǎn)速研究

黨存祿，石 晶

（蘭州理工大學 電氣工程與信息工程學院，蘭州 730050）

風力機是整個風電轉(zhuǎn)換系統(tǒng)中的關(guān)鍵部件[1]。當前主流機型以變槳距變速機組為主，需要復(fù)雜的變槳距系統(tǒng)，機組的成本相對較高，系統(tǒng)可靠性降低。定槳距[2]風力機槳葉與輪轂直接剛性連接，當風速變化時，槳葉的槳距角不發(fā)生變化。定槳距型風力機利用失速性能良好的風力機槳葉，解決了機組在大風時的功率控制問題；葉尖擾流器成功地應(yīng)用在風力發(fā)電機組上，解決了在突甩負載情況下的安全停機問題。且憑借其結(jié)構(gòu)簡單，可靠性高的優(yōu)點，在近20年的風能開發(fā)利用中始終占據(jù)主導(dǎo)地位，被廣泛應(yīng)用。

液壓傳動風力發(fā)電機作為新一代風力發(fā)電設(shè)備[3]，采用液壓柔性傳動裝置，解決塔架頂部設(shè)備、齒輪箱故障及維修問題，省去了傳統(tǒng)機型中齒輪箱、變流器等裝置，減少了塔架頂部設(shè)備的重量及裝機成本。

據(jù)風電行業(yè)人士介紹，德國有400 kW的液壓風電機組運行；美國、丹麥和挪威等國家正在研制階段，未有產(chǎn)品報道；國內(nèi)燕山大學的孔祥東教授團隊針對定量泵-變量馬達閉式系統(tǒng)[4]，在實驗室完成系統(tǒng)工作機理研究，但主要是針對變槳距型液壓風力機。

本文以上述研究為基礎(chǔ)，采用定槳距型液壓傳動風電機組，在槳距角固定的情況下，研究影響轉(zhuǎn)速的原因，要求發(fā)電機能夠?qū)崿F(xiàn)并網(wǎng)，對轉(zhuǎn)速進行控制，使變量馬達以恒速運行，同步并網(wǎng)。

1 定槳距型風力機

由于沒有變槳功能，風力機從風中捕獲的功率表述為[5]

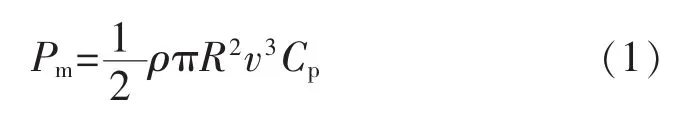
式中：Cp為風能利用系數(shù)，Cp僅由葉尖速比λ決定，λ＝ωR/v，ω 為風力機角速度；R 為葉片半徑；v為風速；ρ為氣流密度。

定槳距風力機輸出功率P曲線規(guī)律如圖1所示，圖中ω*為風力機最優(yōu)角速度，功率曲線只有一點具有最大功率Pmax，變化規(guī)律主要取決于Cp。

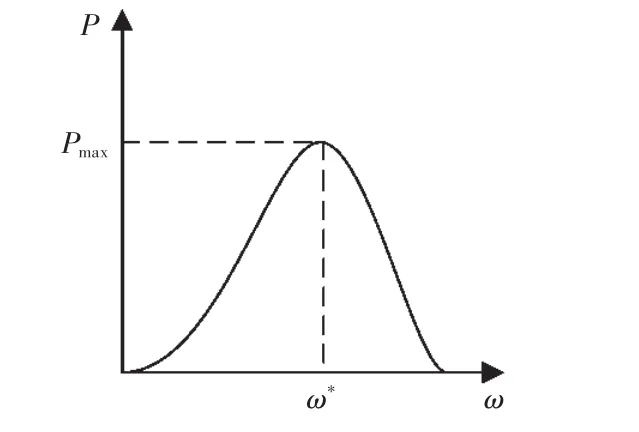
圖1 風力機輸出功率特性曲線Fig.1 Characteristic curve of output power of wind turbine

2 液壓傳動風力發(fā)電機組

2.1 液壓系統(tǒng)工作原理

液壓型風力發(fā)電機組主要包括主傳動系統(tǒng)、偏航系統(tǒng)及剎車安全系統(tǒng)等。

圖2為液壓型風力發(fā)電機組的主傳動系統(tǒng)示意。包括了風力機、定量泵-變量馬達液壓傳動、同步發(fā)電機和發(fā)電控制系統(tǒng)等。定量泵與風力機連接安裝在機艙里，風力機推動定量泵將風能轉(zhuǎn)換為液壓能。變量馬達與同步發(fā)電機安裝在地面上，液壓能傳輸?shù)阶兞狂R達處，驅(qū)動變量馬達轉(zhuǎn)動產(chǎn)生機械能，變量馬達穩(wěn)定輸出轉(zhuǎn)速，同步發(fā)電機并網(wǎng)[6]。

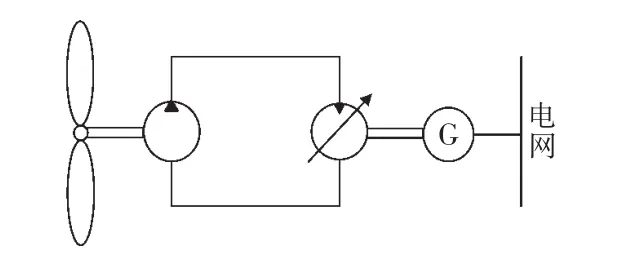
圖2 液壓型風力發(fā)電機組的主傳動系統(tǒng)示意Fig.2 Schematic diagram of main drive system of hydraulic wind turbine

2.2 主傳動數(shù)學模型

推導(dǎo)定量泵-變量馬達系統(tǒng)傳遞函數(shù)時，原理如圖3所示[7]。

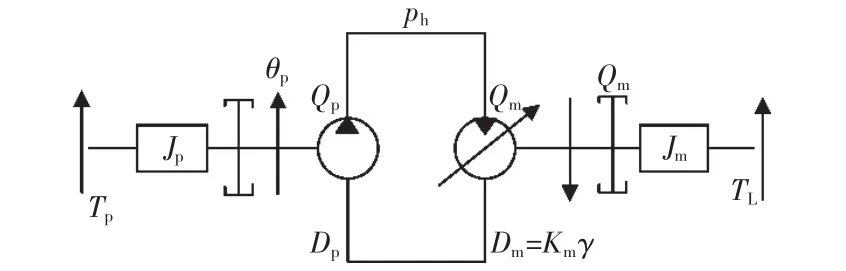
圖3 主傳動系統(tǒng)原理Fig.3 Schematic diagram of main drive system

定量泵流量方程為

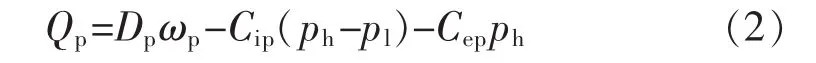
式中：Qp為定量泵流量（m3/s）；Dp為定量泵排量（m3/rad）；ωp為定量泵的轉(zhuǎn)速（rad/s），Cip為定量泵內(nèi)泄露系數(shù)（m3/（s·Pa））；Cep為定量泵外泄露系數(shù)（m3/（s·Pa））；ph為高壓管路壓力（Pa）；pl為低壓管路壓力（Pa）。

定量泵-變量馬達高壓腔流量連續(xù)方程為

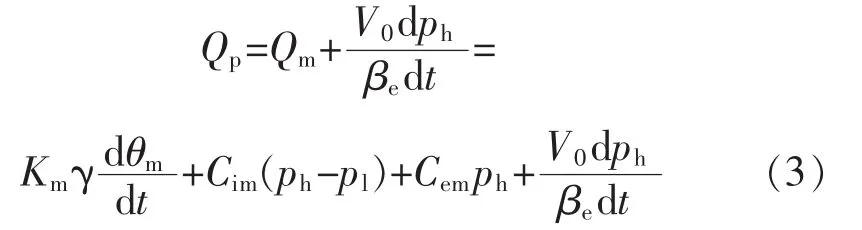
式中：Qm為變量馬達流量（m3/s）；V0為高壓管路的總?cè)莘e（m3）； βe為油液綜合體積彈性模量（Pa）；Qm為變量馬達轉(zhuǎn)角（rad）；Cim為變量馬達內(nèi)泄漏系數(shù)（m3/（s·Pa））；Cem為變量馬達外泄漏系數(shù) （m3/（s·Pa））；Qm為變量馬達的轉(zhuǎn)角（rad）。

變量馬達排量方程為

式中：Dm為變量馬達排量（m3/rad）；Km為變量馬達排量梯度（m3/rad）；γ為變量馬達擺角位置，取值區(qū)間［0，1］。

變量馬達轉(zhuǎn)速方程為

根據(jù)文獻對變量馬達轉(zhuǎn)角θm的推導(dǎo)公式，可知變量馬達轉(zhuǎn)速對斜盤位置傳遞函數(shù)進行拉氏變換為

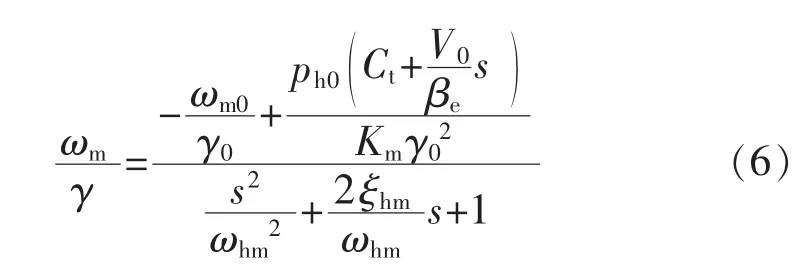
式中：ωhm為變量馬達轉(zhuǎn)速回路固有頻率；ξhm為變量馬達轉(zhuǎn)速回路阻尼比。由于變量γ與乘積成非線性，將其線性化處理得：

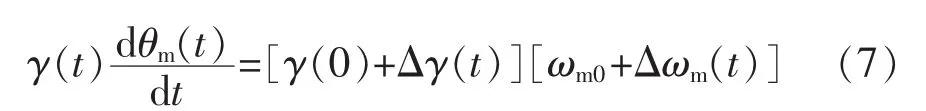
忽略高階無窮小量得：

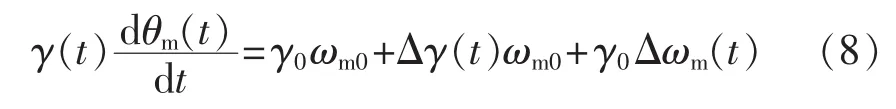
式中：γ0為變量馬達擺角初始值；Δγ（t）為變量馬達的擺角變化值；ωm0為變量馬達初始的轉(zhuǎn)速（rad/s）；Δωm（t）為變量馬達的轉(zhuǎn)速變化值（rad/s）。

變量馬達輸出功率傳遞函數(shù)為

2.3 液壓傳動風力發(fā)電機組控制原理

實現(xiàn)同步并網(wǎng)的要求[8]：①發(fā)電機端電壓大小等于電網(wǎng)電壓；②發(fā)電機頻率與電網(wǎng)頻率一致；③并網(wǎng)合閘時，發(fā)電機與電網(wǎng)回路電勢為零；④發(fā)電機相序與電網(wǎng)相序一致；⑤發(fā)電機電壓波形與電網(wǎng)電壓波形相同。條件④和條件⑤在發(fā)電機設(shè)備選型和制造時已得到了保證。

由上述公式分析可知，風速大小影響了定量泵輸出的流量和壓力，風速越大，定量泵轉(zhuǎn)速越高，流量和壓力越大；定量泵和變量馬達在一個閉環(huán)管路上，變量馬達的開度由斜盤控制器控制，主要控制閉環(huán)管路中的流量，斜盤控制角越大，流量越大，變量馬達轉(zhuǎn)換的功率越大；變量馬達和同步發(fā)電機同軸聯(lián)接，將變量馬達吸收的功率轉(zhuǎn)換為電功率，吸收的越多，發(fā)電機輸出的電功率越大；發(fā)電機輸出電壓大小由同步發(fā)電機的勵磁電流決定；發(fā)電機的頻率由轉(zhuǎn)速決定。

3 液壓型機組轉(zhuǎn)速功率控制方法

由上述分析可知，當定量泵流量為常值時，系統(tǒng)壓力不變，只有變量馬達是變量，改變變量馬達的排量，輸出轉(zhuǎn)速與馬達排量成反比。定量泵轉(zhuǎn)速隨著風速不斷變化輸出不同流量時，變量馬達產(chǎn)生不同轉(zhuǎn)速。按照同步并網(wǎng)要求，需要頻率一定，即需控制馬達轉(zhuǎn)速恒定不變，同步輸出。由式（1）、式（2）知，通過改變馬達的斜盤角度可實現(xiàn)。即輸出轉(zhuǎn)速高低由斜盤控制角決定，輸出轉(zhuǎn)速高，說明控制角偏大，需要調(diào)小，反之亦然。

泵轉(zhuǎn)速變化時，對同一馬達轉(zhuǎn)速對應(yīng)不同變量馬達擺角γ，由式（6）知馬達擺角γ與馬達擺角初始值γ0和擺角變化值Δγ有關(guān)。不同的擺角γ變化時對轉(zhuǎn)速和功率都有影響，采用圖4所示液壓型機組轉(zhuǎn)速功率閉環(huán)控制方法[9]，通過反推理方式，間接用控制器控制斜盤角來控制變量馬達轉(zhuǎn)速和功率。

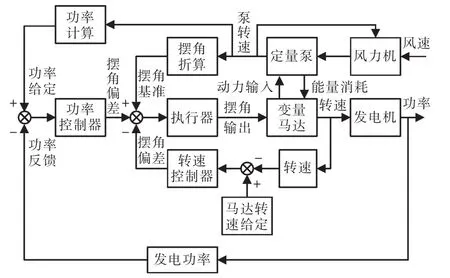
圖4 液壓型機組轉(zhuǎn)速功率閉環(huán)控制方法Fig.4 Speed and power closed loop control method of hydraulic unit

在不斷變化風速下，轉(zhuǎn)速偏差經(jīng)控制器得到擺角變化值Δγ形成馬達擺角微調(diào)量，需要選定的馬達初始值γ0接近工作要求，使其能在小范圍內(nèi)變化。此時若選定一固定的馬達初始值γ0，可能造成Δγ變化過大，無法達到穩(wěn)定調(diào)節(jié)。則需檢測定量泵輸入轉(zhuǎn)速，按流量匹配原則計算所得初始值γ0，作為馬達達到工作范圍要求的初始輸出轉(zhuǎn)速擺角值，γ0-Δγ作為變量馬達擺角控制值。

控制系統(tǒng)設(shè)計的核心內(nèi)容是控制器的選擇及參數(shù)的調(diào)節(jié)，在研究的液壓傳動型風力發(fā)電機組系統(tǒng)中存在非線性，采用PID調(diào)節(jié)所研究的是線性化后的系統(tǒng)模型，且動態(tài)性能和穩(wěn)定性兼顧麻煩，存在矛盾。

因此，采用模糊PID控制方法[10]，結(jié)合傳統(tǒng)PID控制器及模糊控制器優(yōu)點進行優(yōu)化控制。其利用模糊控制器靈活、快速的特點和PID控制器使用的方便性、魯棒性等特點，使其可靠性和性價比更高，易于掌握。

4 控制系統(tǒng)仿真

通過某風力發(fā)電機組生產(chǎn)廠家提供真實風力機數(shù)據(jù)，實施600 kW風力機組主傳動液壓系統(tǒng)為研究對象。變量馬達參數(shù)為排量1000 mL/r，最高壓力42 MPa，馬達輸出轉(zhuǎn)速初值為1500 r/min，采用相似理論確定計算其它實驗數(shù)據(jù)。

根據(jù)數(shù)學模型和控制原理框圖，利用Matlab/Simulink軟件對系統(tǒng)進行仿真。定量泵取一個階躍信號400～410 r/min，通過模糊PID不斷調(diào)節(jié)參數(shù)，變量馬達擺角仿真曲線如圖5所示。

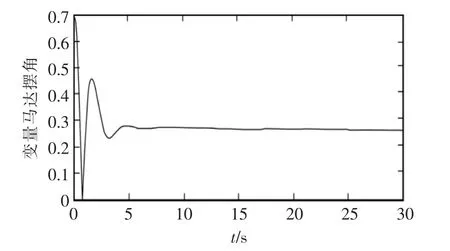
圖5 變量馬達擺角仿真曲線Fig.5 Simulation curve of swing angle of variable motor

通過控制器對馬達擺角的閉環(huán)調(diào)節(jié)控制，變量馬達轉(zhuǎn)速的恒定輸出仿真如圖6所示。可知馬達輸出恒定轉(zhuǎn)速能夠使頻率保持恒定，符合同步并網(wǎng)要求，即對速度影響因素分析控制方法完全可用。

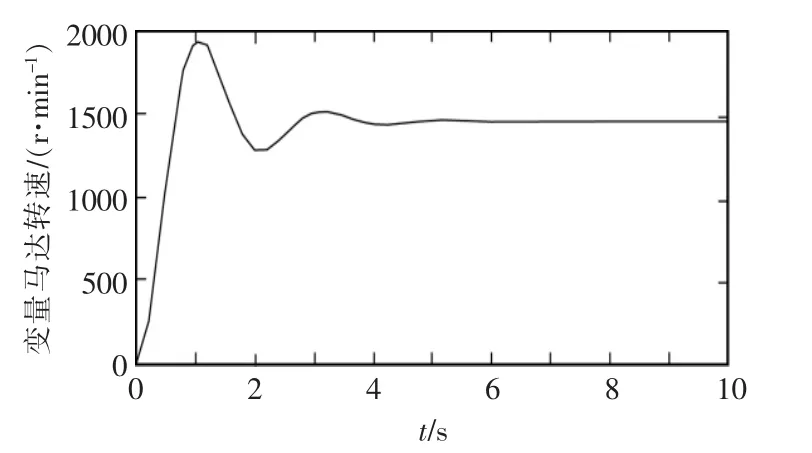
圖6 變量馬達轉(zhuǎn)速仿真曲線Fig.6 Simulation curve of variable motor speed

5 結(jié)語

本文主要介紹了液壓型風力發(fā)電機區(qū)別于傳統(tǒng)風力機的優(yōu)點。用液壓柔性傳動代替了機械剛性傳動，減少了機組的機械故障率，降低了制造和維護成本。選用定槳距機組，機組在整個風速運行范圍里實現(xiàn)與變槳距變速風力機相媲美的功率特性。針對變量馬達恒速運行問題進行分析，通過間接控制馬達擺角變化實現(xiàn)了對變量馬達速度的恒定控制。由于試驗設(shè)備不足，沒有進行試驗驗證，存在不足。

[1]Abdul Motim Howlader，Naomitsu Urasaki，Kousuke Uchida，et al.Parameter identification of wind turbine for maximum powerpoint tracking control[J].Electric Power Components and Systems，2010（38）：603-614.

[2]胡祖榮.定槳距變速風力發(fā)電機組的變速控制技術(shù)研究 [D].江蘇：南京航空航天大學，2010.

[3]Gruet R.The European Wind Energy Association.Wind energy and EU climate policy[R/OL].Print：www.artoos.be.2011：6-8.

[3]艾超，孔祥東，陳文婷，等.液壓型風力發(fā)電機組主傳動系統(tǒng)穩(wěn)速控制研究[J].太陽能學報，2014，35（9）：1757-1763.

[4]賴日新.定槳距變速風力發(fā)電機組的控制技術(shù)研究及其仿真[D].江蘇：南京航空航天大學，2009.

[5]Johannes Schmitz，Nils Vatheuer，Hubertus Murrenhoff.Hydrostatic drive train in wind energy plants[J].Drive Train Components and Power Electronics，2011：1-8.

[6]艾超，閆桂山.液壓型風力發(fā)電機組最優(yōu)功率追蹤控制方法研究[J].動力工程學報，2015，35（2）：126-132.

[7]張剛.液壓型風力發(fā)電機組主傳動系統(tǒng)功率控制研究[D].河北：燕山大學，2012.

[8]艾超.液壓型風力發(fā)電機組轉(zhuǎn)速控制和功率控制研究[D].河北：燕山大學，2012.

[9]張高峰.液壓傳動型風力發(fā)電系統(tǒng)馬達轉(zhuǎn)速特性研究[D].遼寧：大連理工大學，2012.