稀疏數據中基于高斯混合模型的位置推薦框架

,

(1.四川大學 計算機科學與技術學院,成都 610000; 2.南京曉莊學院 新聞傳播學院,南京 210017)

0 概述

在基于位置社交網絡的服務(如Foursquare、Gowalla、Mirco-blogging、大眾點評網等)中,用戶可以分享自己的地理位置信息以及與位置相關的內容?；谖恢蒙缃痪W絡的位置推薦已成為熱點研究[1-4]。

目前,有很多學者對位置推薦進行研究。一些學者采用協同過濾的方法進行位置推薦,對于相似的人可能會有相似的位置偏好。例如,文獻[5]提出了Flap系統,它可推斷社交紐帶并重建整個朋友關系網絡,最后預測用戶的細粒度位置從而進行位置推薦。然而此類研究忽視了用戶的移動模式因素。也有一些學者采用概率模型的方法進行位置推薦,每個人在不同區域簽到符合一定的概率分布規律。例如,文獻[6]利用Twitter中的地理位置信息、發表時間、用戶ID以及文本信息以發現用戶的時空活動行為模式,從而預測用戶在不同區域簽到的概率并進行位置推薦。然而此類研究往往需要建立在健全數據信息的基礎上,否則難以實現有效推薦。

針對稀疏數據,本文基于高斯混合模型(Gaussian Mixture Model,GMM)構建位置推薦框架GMMSD?？紤]用戶的移動模式預測用戶在所有區域簽到的概率分布,并結合用戶之間的協同影響和個人的移動性規律進行位置推薦。

1 相關工作

位置推薦方法主要分為2類:協同過濾和概率模型。

1.1 協同過濾

文獻[7]提出融合矩陣分解(Matrix Factoriza-tion,MF)模型,首先捕捉地域影響力,然后考慮社交信息建立矩陣分解模型,從而進行個性化位置推薦。文獻[8]提出SeqRWR方法動態選擇在每個時間片對目標用戶最有影響力的N個朋友,然后利用所構建的TSB模型對朋友影響力的特征建模,在每個時間片對用戶進行位置推薦。文獻[9]構建IRenMF方法探究周邊地理位置的特征,學習用戶和位置的潛因子以提高位置推薦的準確度。文獻[10]構建GeoMF模型,首先利用所提的加權矩陣分解解決隱式反饋協同過濾POI推薦的稀疏性問題,然后將空間聚類現象融入到矩陣分解模型中以提高推薦性能。文獻[11]實現了基于用戶偏好并且時間敏感的推薦系統。該系統考慮了位置的流行度、用戶的偏好、用戶的朋友、用戶訪問位置的時間特征4個因素,為用戶做特定時間的位置推薦。文獻[12]提出了基于位置和偏好感知的推薦系統。該系統同時考慮了用戶個人偏好和本地專家的意見。

不同于以上的協同過濾方法,本文框架考慮用戶的移動模式,能預測用戶在所有區域簽到的概率分布并進行位置推薦。

1.2 概率模型

文獻[4]提出了LORE方法。該方法從用戶簽到位置序列中挖掘序列模式并構建馬爾科夫鏈,最后結合地理和社交影響建立模型從而進行位置推薦。文獻[6]利用微博中的內容、用戶ID、時間、地理位置信息進行建模,構建W4模型從而為用戶進行位置推薦。文獻[13]構建PMM模型,利用用戶周期性移動特性在不同時間段為用戶進行位置推薦。

本文框架考慮相似用戶的協同作用對推薦性能的影響,并能在稀疏數據集上進行有效推薦。

2 GMMSD框架

2.1 工作原理

本文位置推薦框架的工作原理如下:

1)將用戶歷史簽到數據按4個時間段分為4個部分。

2)對城市空間進行網格劃分和序列化,經過噪聲過濾后再根據用戶的時間片簽到數據得到用戶-區域矩陣。

3)運用矩陣分解填充稀疏值,得到分解后的用戶-區域矩陣。

4)采用K-Means聚類算法得到每個用戶的簽到聚類中心。

5)利用高斯混合模型建模,針對每個區域,計算二重積分得到用戶在區域簽到的概率。

6)Top-k概率值對應的區域即為推薦位置。

2.2 數據預處理

定義1(區域) 將整個城市空間S劃分成N個相同的單元正方網格r(例如:200 m×200 m),該單元正方網格稱為區域。每個經緯度對都會映射到唯一的區域。

定義2(區域序列化) 將N個單元正方網格區域r橫向展開為n元有限序列R=(r1,r2,…,rn),該過程稱為區域序列化。序列R稱為區域序列,序列元素值表示所有用戶在該區域簽到的次數。

定義3(噪聲過濾) 將區域序列中元素值為0的元素去掉的過程稱為噪聲過濾。

定義4(簽到區域序列) 用戶到噪聲過濾后區域序列對應的區域簽到的次數排列稱為簽到區域序列。

圖1描述了數據預處理的過程,其中主要包括4個步驟:1)將城市空間劃分為N個區域;2)區域序列化;3)噪聲過濾;4)生成簽到區域序列。

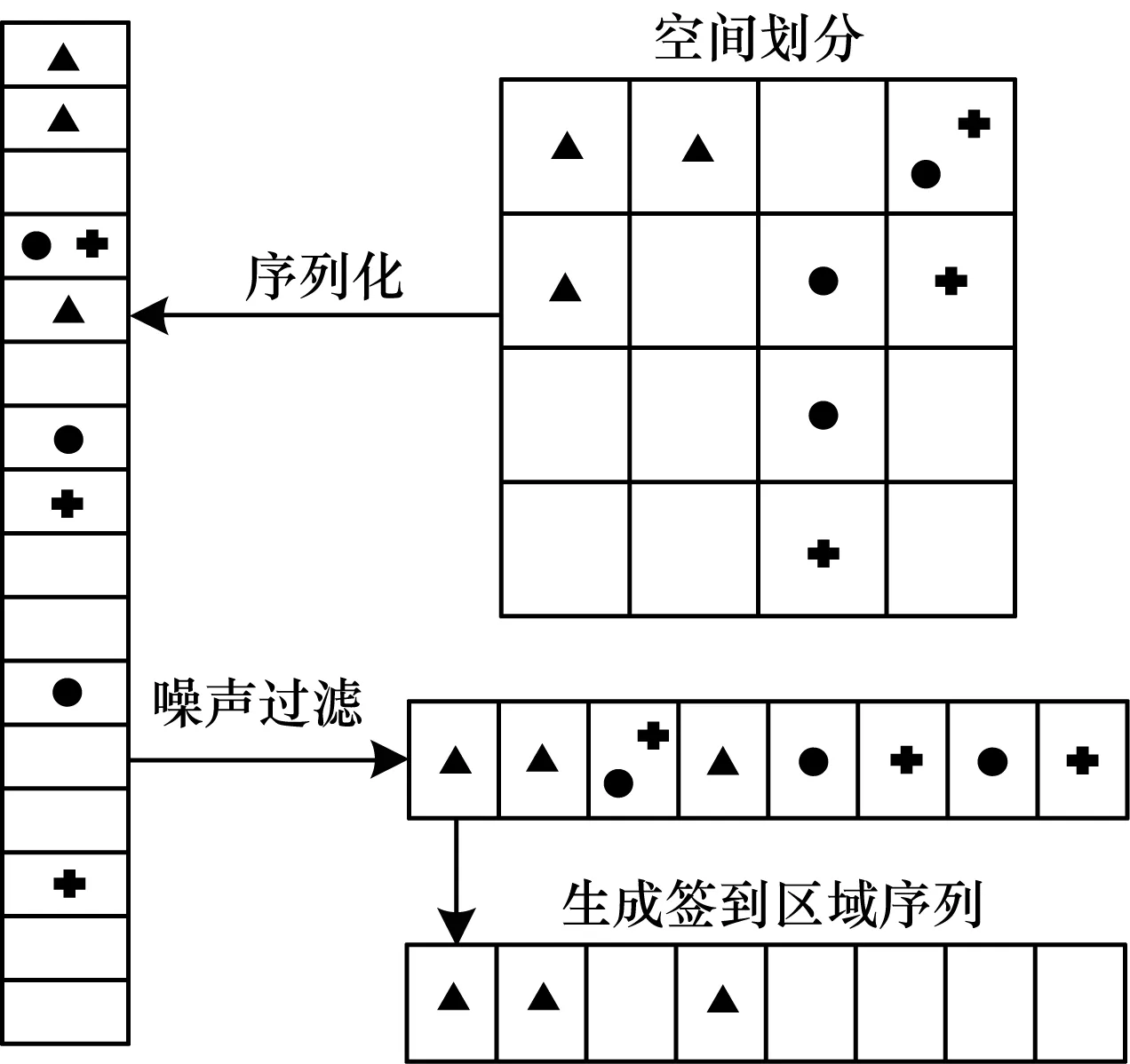
圖1 數據預處理過程

2.3 稀疏數據處理

根據用戶簽到數據所得到的每個用戶的簽到區域序列往往是稀疏的。本文采用矩陣分解的方法予以解決。用戶-區域矩陣定義如下:

定義5(用戶-區域矩陣) 根據每個用戶的簽到數據,得到每個用戶的R元簽到區域序列。U個用戶的簽到區域序列構成一個用戶-區域矩陣CU×R。矩陣元素值Cij表示用戶i到區域j簽到的次數。

矩陣分解假設每個用戶的特征都可以由若干個因子進行刻畫,而每個區域的特征同樣可以使用相同數量的因子加以表示。當一個用戶的特征和一個區域的特征相吻合時,就認為這個用戶會以高頻次去該區域,反之亦然。矩陣分解目標就是把用戶-區域矩陣C分解為用戶因子矩陣P和區域因子矩陣Q的乘積。一般表示為:

C?PQT

(1)

其中,P∈U×D,Q∈R×D,D為刻畫每個用戶或每個區域特征的因子數。一般D的取值遠小于U或R。用戶在區域簽到的真實頻次和預測頻次之間的差值e服從正態分布,即e～N(0,σ2),其等價于當用戶-區域矩陣C非常稀疏時,就會出現過擬合問題。為降低模型的過度擬合,本文采用正則化的方法,最小化以下目標函數:

其中,λ為正則項的權重,稱為懲罰參數。

下面使用梯度下降法進行求解。獲得用戶和區域因子矩陣P和Q后,使用式(2)計算用戶u出現在區域r的頻次:

(2)

此處梯度下降法的具體推導不再贅述,用戶因子矩陣P和區域因子矩陣Q的更新公式如下:

Pud=Pud+η·(eur·Qrd-λ·Pud)

(3)

Qrd=Qrd+η·(eur·Pud-λ·Qrd)

(4)

梯度下降法中最小化的具體步驟見算法1。

算法1矩陣分解(MF)

輸入用戶-區域矩陣CU×R,潛因子數D,懲罰參數λ和學習率η

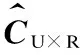
1.初始化P、Q;

2.REPEAT

3. FOREACH用戶-區域對(u,r)∈P

5. 計算預測頻次誤差eur;

6. 依據式(3)更新用戶因子向量Pu;

7. 依據式(4)更新區域因子向量Qr;

8. END FOREACH

9.UNTIL滿足停止條件

2.4 高斯混合模型

即使用戶移動具有多樣性,但是由于用戶偏好和地理條件的限制,用戶移動會呈現一定的模式[13]。為提高預測的性能,本文引入高斯混合模型來研究用戶的移動模式。

用戶的簽到情況往往是圍繞幾個中心區域分布的,通常需要利用多個高斯過程,即高斯混合模型來表示。用戶的簽到樣本數據集R={r1,r2,…,rn}符合該用戶的移動模式。這里,區域r由該區域的中心經緯度表示,即r=(x,y),其中x為該坐標點的緯度,y為該坐標點的經度。GMM模型公式如下:

(5)

(6)

通常采用EM算法逐步迭代逼近最大值對參數進行求解。

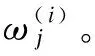
(7)

EM算法的M步:更新參數φj=(αj,μj,Σj)。

(8)

(9)

(10)

算法2高斯混合模型(GMM)

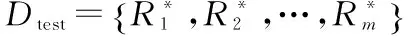
輸出用戶在測試集中每個區域簽到的概率、推薦均方根誤差RRMSE和平均絕對誤差MMAE

1.FOR u←1 TO m /*循環每個用戶,已知該用戶的訓練簽到樣本數據集Ru={r1,r2,…,rn}*/

2.利用K-Means算法確定k個聚類中心;

3.初始化GMM的模型參數Φ;

4. REPEAT

5. FOR i←1 TO n

7. END FOR

8. FOR j←1 TO k

9. 依據式(8)更新αj;

10. 依據式(9)更新μj;

11. 依據式(10)更新Σj;

12. END FOR

13. UNTIL滿足停止條件

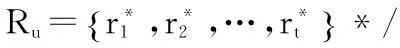
15. 將式(5)作為被積函數計算二重積分,得出用戶出現在測試集中每個區域的概率;

16. 計算每個用戶的推薦誤差eru和emu;

17. END FOR

20.END FOR

本文結合矩陣分解和高斯混合模型建立的位置推薦GMMSD框架,相比于矩陣分解模型考慮了用戶的移動模式,使用戶的簽到情況更符合用戶真實的移動規律;相比于高斯混合模型考慮了相似用戶的協同影響,能在稀疏數據上進行有效推薦。

3 實驗與結果分析

3.1 數據集

本文使用基于位置社交應用BrightKite和Gowalla中紐約城市的簽到數據(具體信息如表1所示),從中隨機選擇30%的用戶簽到記錄訓練模型,再從剩余70%的用戶簽到記錄中按時間選取每個用戶前70%的簽到記錄作為模型參數驗證數據集,剩余的30%數據作為測試集。

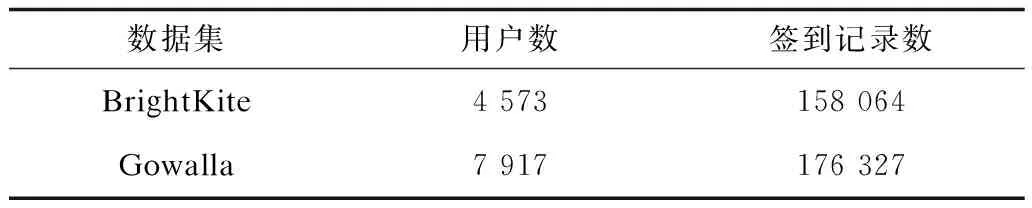
表1 實驗數據集

3.2 評價指標

為評價不同方法的推薦性能,本文使用2個評價指標,即均方根誤差RRMSE和平均絕對誤差MMAE,分別如式(11)和式(12)所示。

(11)

(12)

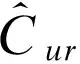
3.3 對比算法

本文將GMMSD框架和以下方法進行對比:

1)協同過濾算法(CF)[11]:相似的用戶間可能會有相同的位置偏好。該算法基于社交關系,用戶會以很大概率到朋友去過的區域簽到。

2)張量分解算法(TD)[14-15]:針對用戶簽到的特征集,將其集成到一個三維張量中,三維分別是用戶、區域和時間。運用張量分解填充稀疏值,得到特定時間值的用戶區域概率矩陣。

3)矩陣分解算法(MF)[7,9,16]:該算法是本文提出框架的基礎,它可以很好地解決數據稀疏性問題,對用戶-區域矩陣,運用該算法計算用戶到每個區域的頻次,最后歸一化處理得到每個用戶到不同區域的概率,Top-k概率值對應的區域即為推薦位置。

4)高斯混合模型(GMM)[17-18]:根據用戶的簽到數據對用戶進行移動性建模,然后計算二重積分,得到用戶在不同區域簽到的概率，從而進行位置推薦。

3.4 參數調整

在本文框架中,本文將用戶歷史簽到數據按4個時間段(T1～T4)劃分為4個部分。其中:T1表示時間段0:00—6:00;T2表示時間段6:00—12:00;T3表示時間段12:00—18:00;T4表示時間段18:00—24:00。通過實驗設置學習率η=0.001,懲罰參數λ=0.005。此外,本文還需要設置2個參數,即潛因子個數D和聚類中心個數K。隨機選取每個用戶30%的簽到記錄訓練參數。在4個時間段內參數調整對推薦性能的影響如圖2～圖5所示。

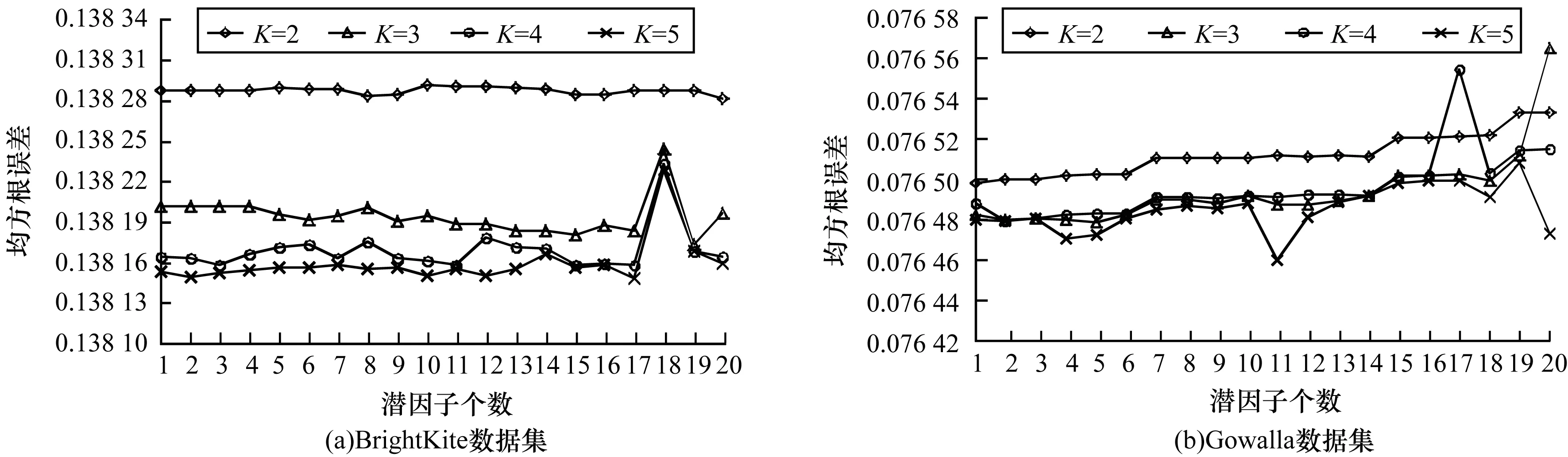
圖2 時間段T1內參數調整對推薦性能的影響

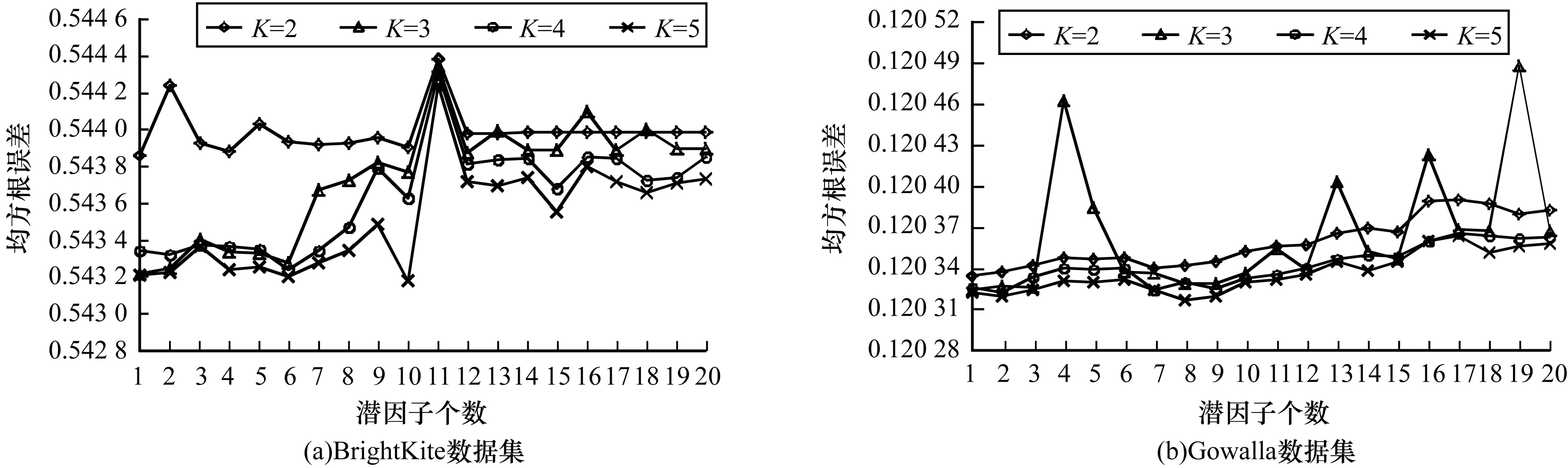
圖3 時間段T2內參數調整對推薦性能的影響

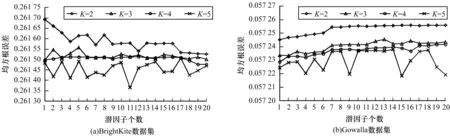
圖4 時間段T3內參數調整對推薦性能的影響

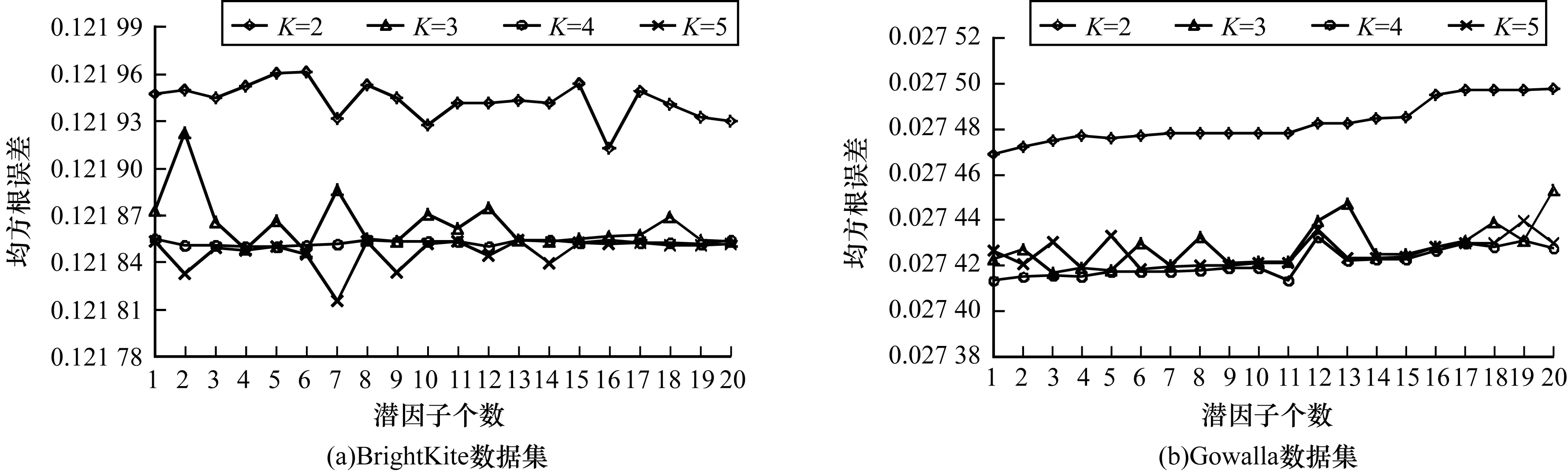
圖5 時間段T4內參數調整對推薦性能的影響

圖2～圖5顯示了在2個驗證數據集下不同時間段設置不同的聚類個數時RRMSE隨潛因子個數變化的結果。為了使本文所提的GMMSD框架的推薦性能夠達到最優,即使RRMSE的誤差值最小,因此,通過觀察圖2～圖5,本文將參數調整如表2所示。

表2 參數調整結果

3.5 實驗結果

本文比較了4種方法(CF、TD、MF和GMMSD)的推薦性能。每種方法的均方根誤差和平均絕對誤差如圖6～圖7所示,可以看到GMMSD的推薦性能優于當前其他方法。為驗證用矩陣分解填充數據的合理性,本文選取了相對較稠密的用戶簽到記錄進行實驗,比較2個數據集下的GMM和GMMSD推薦誤差情況,如圖8所示。

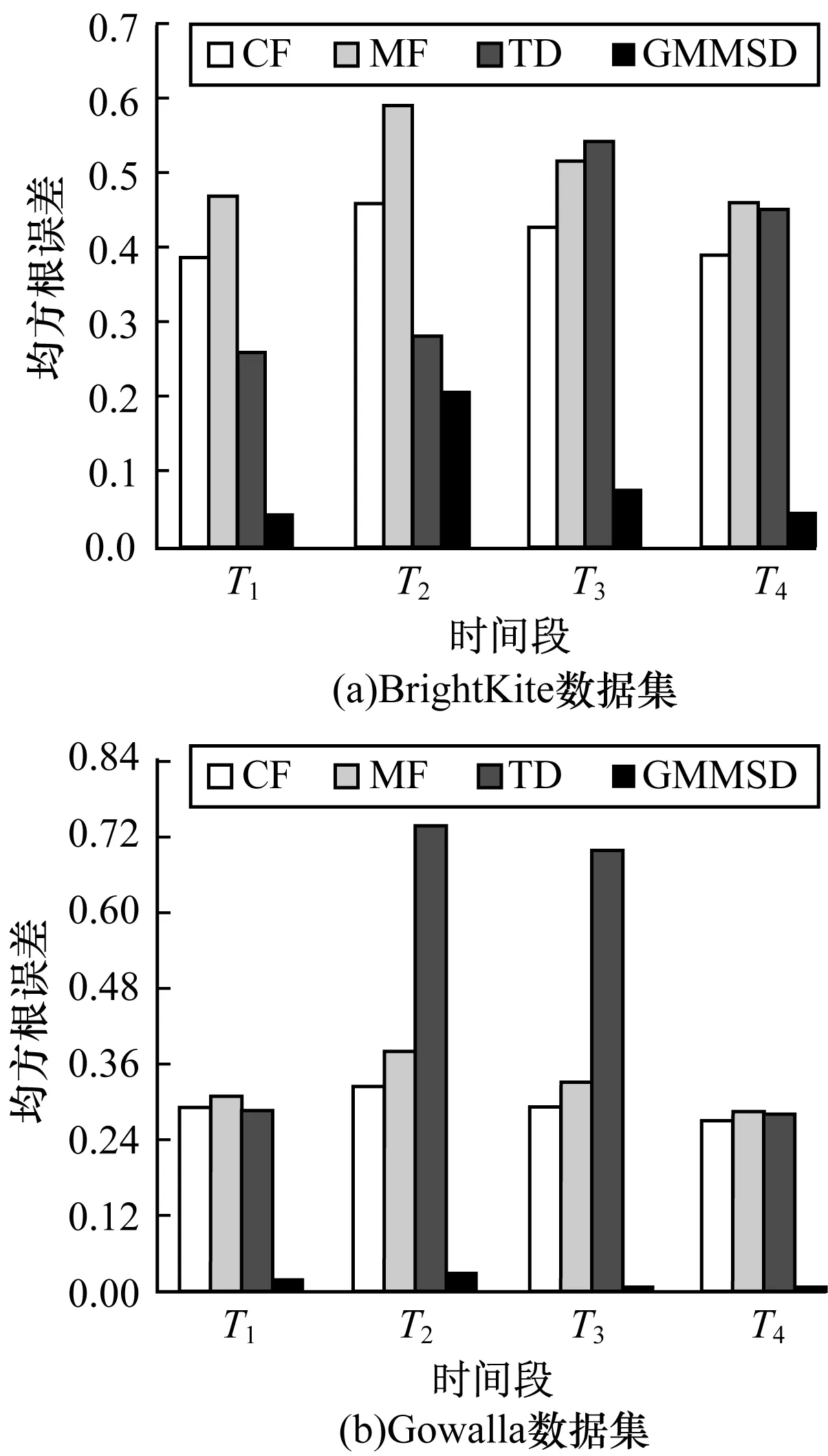
圖6 均方根誤差對比

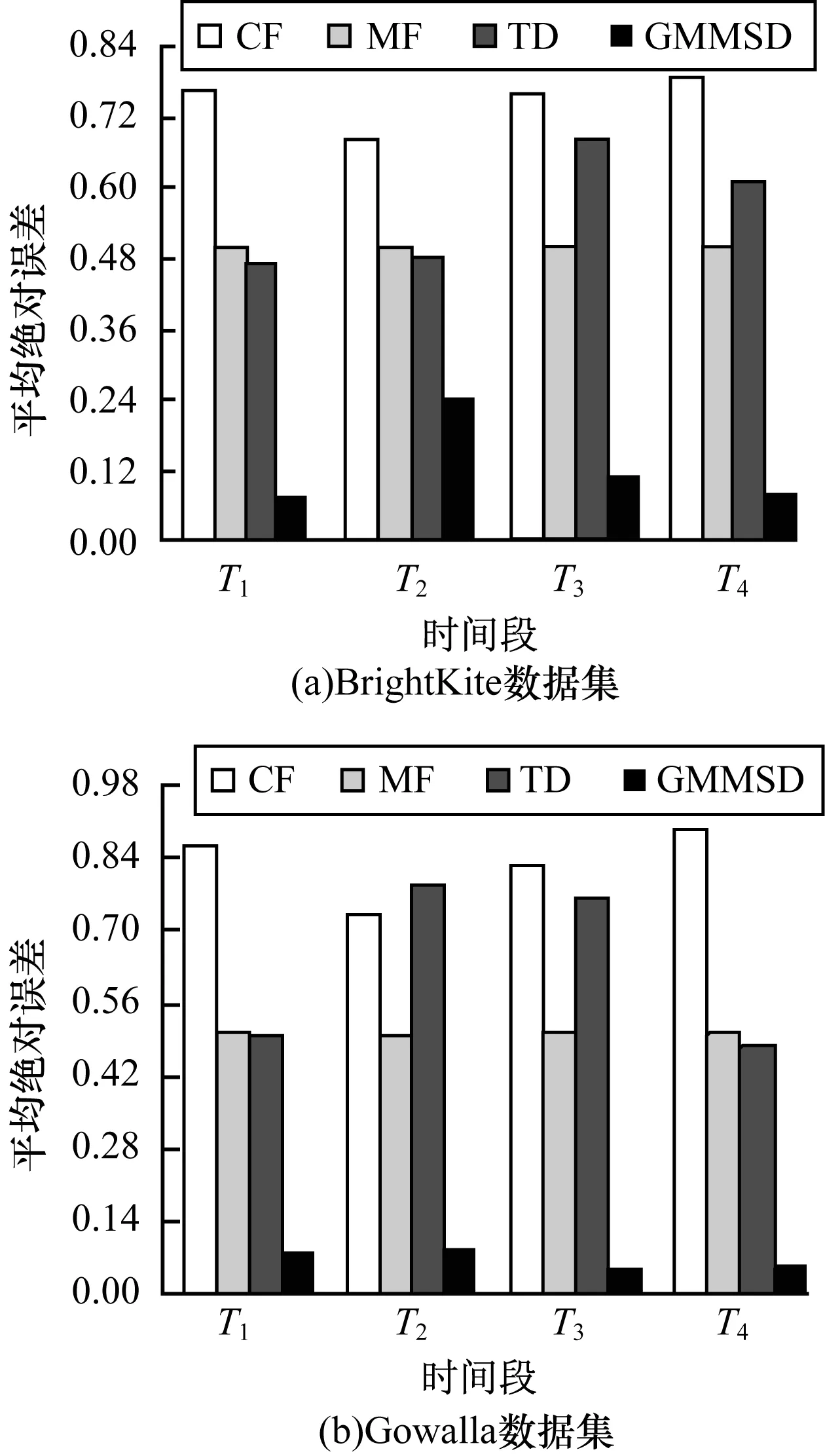
圖7 平均絕對誤差對比

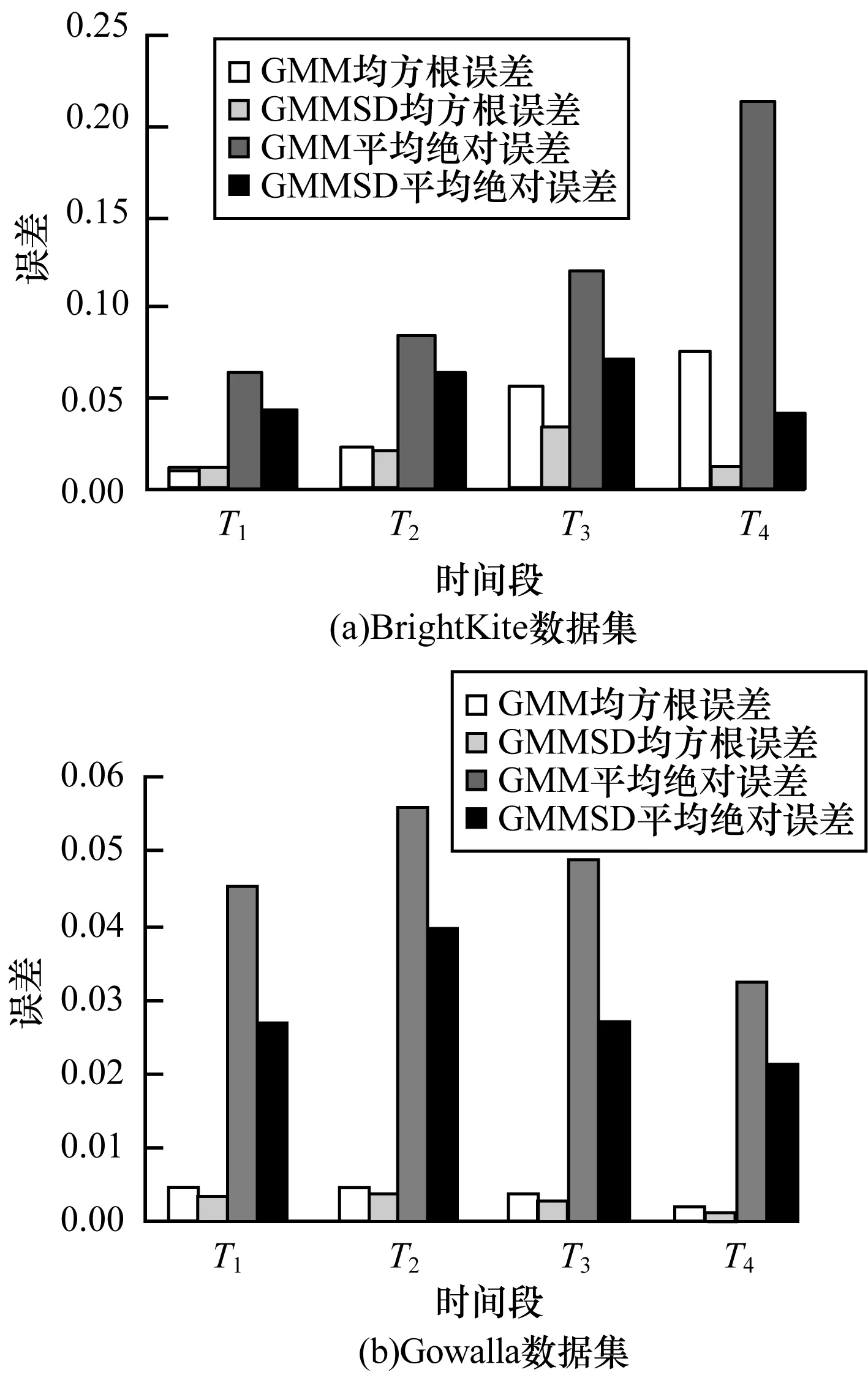
圖8 GMM和GMMSD框架的推薦誤差對比

由上述結果可知，CF面臨著冷啟動問題,無法對沒有社交關系的新用戶進行位置推薦。而TD和MF都沒有考慮用戶的移動模式,分解后的簽到情況不符合用戶的移動性規律。GMM只考慮了用戶個體的移動性,沒有考慮社會信息的影響并且該模型不適用于稀疏數據。而GMMSD性能較優的原因為:GMMSD同時考慮了相似用戶的協同推薦和用戶的移動模式,并能在稀疏數據上進行有效推薦，因此其性能較優。

4 結束語

本文構建一種稀疏數據中基于GMM的位置推薦框架。該框架結合了矩陣分解和高斯混合模型的優點,同時考慮了相似用戶的協同推薦和用戶個體的移動模式。首先將用戶簽到數據按時間段分片,再對城市空間進行區域劃分和序列化,經過噪聲過濾后得到用戶-區域矩陣;然后利用矩陣分解建模用戶之間的協同關系,在一定程度上緩解了數據稀疏問題;最后使用K-Means算法找到聚類中心并采用高斯混合模型計算每個用戶出現在不同區域的概率,從而進行位置推薦。在真實數據集上的實驗結果表明,本文框架考慮了社會信息和用戶個體移動規律的共同影響,可在稀疏數據上進行有效位置推薦,并且準確度較高。后續研究將考慮加入社交網絡信息,以進一步提高推薦準確度。

[1] RAHIMI S M,WANG X.Location Recommendation Based on Periodicity of Human Activities and Location Categories[M]//PEI J,TSENG V S,CAO L.Advances in Knowledge Discovery and Data Mining.Berlin,Germany:Springer,2013:377-389.

[2] JIE B,YU Z,WILKIE D,et al.A Survey on Recommendations in Location-based Social Networks[J].GeoInformatica,2015,19(3):525-565.

[3] ZHANG J,CHOWMEMBER C,LI Y.iGeoRec:A Personalized and Efficient Geographical Location Recommendation Framework[J].IEEE Transactions on Services Computing,2015,8(5):701-714.

[4] ZHANG J D,CHOW C Y,LI Y.LORE:Exploiting Sequential Influence for Location Recommendations[C]//Proceedings of the 22nd ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems.New York,USA:ACM Press,2014:103-112.

[5] SADILEK A,KAUTZ H,BIGHAM J P.Finding Your Friends and Following Them to Where You Are[C]//Proceedings of the 5th International Conference on Web Search and Web Data Mining.Seattle,USA:DBLP,2012:723-732.

[6] YUAN Q,CONG G,MA Z,et al.Who,Where,When and What:Discover Spatio-Temporal Topics for Twitter Users[C]//Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York,USA:ACM Press,2013:605-613.

[7] CHENG C,YANG H,KING I,et al.Fused Matrix Factorization with Geographical and Social Influence in Location-based Social Networks[C]//Proceedings of the 26th AAAI Conference on Artificial Intelligence.Toronto,Canada:AAAI Press,2012:17-23.

[8] JIA Y,WANG Y,JIN X,et al.Location Prediction:A Temporal-Spatial Bayesian Model[J].ACM Transactions on Intelligent Systems & Technology,2016,7(3):31.

[9] LIU Y,WEI W,SUN A,et al.Exploiting Geographical Neighborhood Characteristics for Location Recom menda-tion[C]//Proceedings of the 23rd ACM International Conference on Information and Knowledge Management.New York,USA:ACM Press,2014:739-748.

[10] LIAN D,ZHAO C,XIE X,et al.GeoMF:Joint Geographical Modeling and Matrix Factorization for Point-of-Interest Recommendation[C]//Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York,USA:ACM Press,2014:831-840.

[11] ZHANG S,REN K.User Preferences-based and Time-sensitive Location Recommendation Using Check-in Data[J].Journal of Computer & Communications,2015,3(9):18-27.

[12] BAO J,ZHENG Y,MOKBEL M F.Location-based and Preference-aware Recommendation Using Sparse Geo-social Networking Data[C]//Proceedings of the 20th International Conference on Advances in Geographic Information Systems.New York,USA:ACM Press,2012:199-208.

[13] CHO E,MYERS S A,LESKOVEC J.Friendship and Mobility:User Movement in Location-based Social Networks[C]//Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.San Diego,USA:DBLP,2011:1082-1090.

[14] ZHONG Y,YUAN N J,ZHONG W,et al.You Are Where You Go:Inferring Demographic Attributes from Location Check-ins[C]//Proceedings of the 8th ACM International Conference on Web Search and Data Mining.New York,USA:ACM Press,2015:295-304.

[15] ZHENG V W,CAO B,ZHENG Y,et al.Collaborative Filtering Meets Mobile Recommendation:A User-centered Approach[C]//Proceedings of 24th AAAI Conference on Artificial Intelligence.Atlanta,USA:AAAI,2010:236-241.

[16] 陳 蕓,董西偉,荊曉遠.聯合混合范數約束和增量非負矩陣分解的目標跟蹤[J].計算機工程,2015,41(12):260-264.

[17] 喬少杰,金 琨,韓 楠,等.GMTP:基于高斯混合模型的軌跡預測算法[J].軟件學報,2015,26(5):1048-1049.

[18] 冀續燁,陳 明,馮國富,等.一種多模型協同的目標提取方法[J].計算機工程,2015,41(5):254-258.