彈性抗滑樁樁底支承條件對其內力和位移的影響分析

焦世杰，蘇愛軍，何 嘯

(中國地質大學(武漢)教育部長江三峽庫區地質災害研究中心，湖北 武漢 430074)

抗滑樁作為一種橫向受荷樁，由于具有抗滑能力強、樁位布設靈活、施工方便、適用于滑面較深的大型滑坡等多方面的突出優點，已被廣泛應用于滑坡地質災害的治理工程實踐中[1-3]。而抗滑樁設計中，樁身內力計算是決定設計成敗的關鍵因素。目前，抗滑樁內力計算的方法有很多，如懸臂樁法、地基系數法、雙參數法[4]，p-y曲線法、有限單元法[5]等。其中，懸臂樁法由于出現時間早且計算簡單，目前在實際工作中應用最多。該方法根據對嵌固段地基系數假定的不同，又分為“K”法、“m”法和“C”法。本文主要對工程中應用較多的“K”法進行討論。

對抗滑樁進行內力計算時，嵌固段樁底支承條件可分為自由支承、鉸支承和固定支承。而抗滑樁工程設計中，設計人員一般都是根據經驗選取抗滑樁樁底支承條件，但樁底支承條件選取不同，則抗滑樁嵌固段樁身內力和位移也不同。若樁底支承條件選取不當，則會造成計算出的抗滑樁樁身內力和位移與實際相差很大，最終導致抗滑樁配筋過多，增加工程投資。抗滑樁樁底支承條件取決于抗滑樁嵌固段長度以及嵌固段巖體的地基系數，而嵌固段巖體的地基系數又與嵌固段巖體力學性質、風化破碎程度和地下水[6-7]等因素有關，因此分析抗滑樁在各種因素下樁底不同支承條件對抗滑樁樁身內力和位移的影響具有重要意義。但限于篇幅，本文針對工程實際中的常見情況，只討論嵌固段巖體微風化、嵌固段長度為樁全長的1/3這類情況，并結合具體的工程實例，探討樁底不同支承條件和地基系數情況下，抗滑樁樁身內力和位移的變化規律。

1 抗滑樁受荷段樁身內力和位移的計算

抗滑樁受荷段樁后滑坡推力和樁前巖土體抗力的分布形式與滑坡的類型、部位和地層性質等因素有關，可分為矩形、梯形和三角形分布[8-11]。本文在計算抗滑樁樁身內力時，建立了兩個獨立的坐標系：計算受荷段的內力時，其坐標系以樁頂(O點)為原點，沿樁中心豎直向下為y軸；計算嵌固段的內力時，其坐標系以嵌固段頂面(A點)為原點，沿樁中心豎直向下為y軸。如圖1所示，其中O點表示樁身頂部位置，A點表示樁身在滑面的位置，B點表示樁身底部位置。本文假定抗滑樁受荷段樁后滑坡推力分布形式為矩形，樁前巖土體抗力分布形式為三角形，受荷段的內力依據懸臂梁理論[12-13]進行計算，則抗滑樁樁身變形的微分方程可表示為

圖1 抗滑樁受力分析圖Fig.1 Diagram of stress analysis of the anti-slide pile

d2xdy2=-M(y)EI

(1)

式中：M(y)為抗滑樁樁身任意點處的彎矩(kN·m)；EI為抗滑樁樁身抗彎剛度(kN·m)。

抗滑樁受荷段樁身內力和位移的計算如下所述：

(1) 當樁前巖土體可能滑走時(無剩余抗滑力)，則有:

Qy=qy

My=12qy2

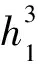
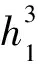
(2)

式中：Qy、My、φy、xy分別為抗滑樁樁身任一截面處的剪力(kN)、彎矩(kN·m)、轉角(rad)和位移(m)；h1為抗滑樁受荷段長度(m)；q為抗滑樁受荷段樁后滑坡推力的均布荷載值(kN/m)；φA為抗滑樁在滑面處(A點)的轉角(rad)；xA為抗滑樁在滑面處(A點)的位移(m)；其他符號意義同前。

(2) 當樁前巖土體基本穩定時(有剩余抗滑力)，則有

Qy=qy-q1(y-h3)22(h1-h3)

My=12qy2-q1(y-h3)36(h1-h3)

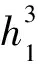
[(y-h3)4-(h1-h3)4]

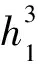
q1120EI(h1-h3)[(y-h3)5-5y(h1-h3)4+

(h1-h3)4(4h1+h3)]

(3)

式中：h3為樁前巖土體頂面距抗滑樁頂面的距離(m)；q1為抗滑樁受荷段樁前巖土體抗力底部荷載值(kN/m)；其他符號意義同前。

2 抗滑樁嵌固段樁身內力和位移的計算

對于彈性抗滑樁，樁頂受水平荷載的撓曲微分方程可表示為[12]：

EId4xdy4+KBpx=0

(4)

式中：K為抗滑樁嵌固段巖體的地基系數(kN/m3)；Bp為抗滑樁正面計算寬度(m)；其他符號意義同前。

由于抗滑樁變形系數β=4KBp4EI，則公式(4)可寫成：

d4xdy4+4β4x=0

(5)

公式(5)為4階齊次常系數線性微分方程，其中β為區分剛性樁和彈性樁的變形系數。通過數學求解可得到抗滑樁嵌固段任一截面處的樁身內力和位移，即

Qy=β3EI(QAβ3EIa1-4xAa2-4φAβa3-4MAβ2EIa4)

My=β2EI(MAβ2EIa1+QAβ3EIa2-4xAa3-4φAβa4)

φy=β(φAβa1+MAβ2EIa2+QAβ3EIa3-4xAa4)

xy=xAa1+φAβa2+MAβ2EIa3+QAβ3EIa4

(6)

其中：a1=cosβychβy;

a2=12(sinβychβy+cosβyshβy);

a3=12sinβyshβy;

a4=14(sinβychβy-cosβyshβy).

式中：QA、MA、φA、xA分別為抗滑樁在滑動面處樁身的剪力(kN)、彎矩(kN·m)、轉角(rad)和位移(m)；a1、a2、a3、a4的取值可參考文獻[1]；其他符號意義同前。

公式(6)中φA和xA是通過抗滑樁樁底支承條件確定的。抗滑樁樁底支承條件有以下3種：

(1) 樁底為自由支承：QB=0，MB=0。

(2) 樁底為鉸支承：MB=0，xB=0。

(3) 樁底為固定支承：xB=0，φB=0。

根據上述抗滑樁樁底支承條件，即可求得抗滑樁嵌固段樁身任一截面處的內力和位移。

3 工程實例應用與分析

本文以三峽庫區秭歸縣水田壩鄉譚家灣滑坡為例，利用MATLAB軟件分別計算了樁底不同支承條件和地基系數情況下抗滑樁樁身內力和位移，并進行了對比分析。

該滑坡堆積體主要為碎塊石土夾黏性土，基巖主要為侏羅系上統蓬萊鎮組的長石石英砂巖。通過工程地質類比和反演分析法綜合確定了該滑坡滑帶土的抗剪強度參數[14-15]，即天然狀態下滑帶土黏聚力為15 kPa、內摩擦角為26°，飽和狀態下滑帶土黏聚力為13 kPa、內摩擦角為24°。經計算，該滑坡推力水平分量為1 196.28 kN/m3，而抗滑樁截面尺寸為1.8 m(寬)×2.5 m(高)，抗滑樁受荷段長12 m、嵌固段長6 m，樁中心距為5 m。

本文利用所編制的程序，通過改變抗滑樁嵌固段巖體的地基系數K值，計算抗滑樁在不同的樁底支承條件下樁身內力和位移。表1為抗滑樁在不同地基系數和支承條件下樁身的最大內力，圖2至圖10為抗滑樁在不同地基系數和支承條件下樁身內力和位移的變化情況，圖11至圖13為地基系數K值為140 MN/m3時抗滑樁在不同支承條件下樁身內力和位移的變化情況。

表1 抗滑樁在不同地基系數和支承條件下樁身的 最大內力

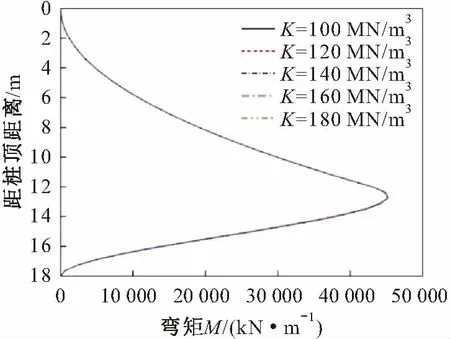
圖2 抗滑樁在不同地基系數下的彎矩圖(自由支承)Fig.2 Bending moment diagram under different foundation coefficients (free bearing)

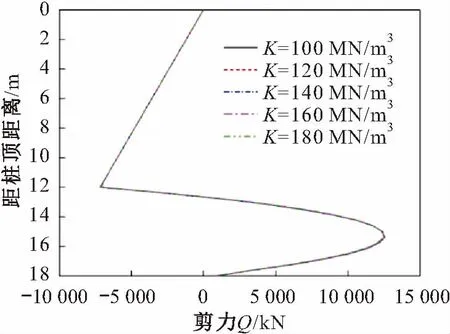
圖3 抗滑樁在不同地基系數下的剪力圖(自由支承)Fig.3 Shear diagram under different foundation coefficients (free bearing )

圖4 抗滑樁在不同地基系數下的位移圖(自由支承) Fig.4 Displacement diagram under different foundation coefficients (free bearing)

圖5 抗滑樁在不同地基系數下的彎矩圖(鉸支承)Fig.5 Bending moment diagram under different foundation coefficients (hinged bearing)

由圖2至圖4可見，對于樁底約束為自由支承的抗滑樁，當抗滑樁嵌固段長度一定時，地基系數K值的變化對抗滑樁嵌固段樁身彎矩M和剪力Q的影響很小，即隨著K值的增加，抗滑樁嵌固段樁身彎矩逐漸減小，K值每增加20 MN/m3，隨著深度的增加，其彎矩減小的百分比越大，最大為0.5%，而抗滑樁嵌固段樁身剪力先增大后減小，在靠近滑面的位置剪力變化的百分比最大，為3.81%；地基系數K值的變化對抗滑樁樁身位移的影響較大，即隨著K值的增加，抗滑樁嵌固段樁身位移逐漸減小，且其減小速率逐漸減慢，K值每增加20 MN/m3，隨著深度的增加，抗滑樁嵌固段樁身位移減小的百分比普遍大于受荷段，最大為19.14%。

圖6 抗滑樁在不同地基系數下的剪力圖(鉸支承)Fig.6 Shear diagram under different foundation coefficients (hinged bearing)

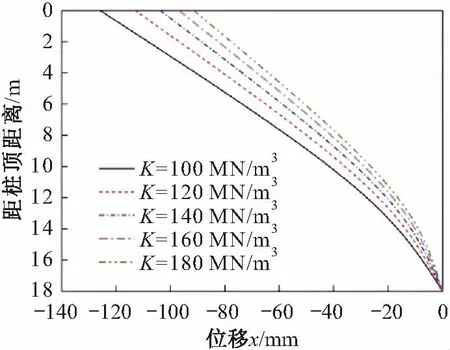
圖7 抗滑樁在不同地基系數下的位移圖(鉸支承)Fig.7 Displacement diagram under different foundation coefficients (hinged bearing)

由圖5至圖7可見，對于樁底約束為鉸支承的抗滑樁，當抗滑樁嵌固段長度一定時，地基系數K值的變化對抗滑樁嵌固段樁身彎矩M和剪力Q的影響也很小，但比樁底約束為自由支承的抗滑樁的影響要大，即隨著K值的增加，抗滑樁嵌固段樁身彎矩逐漸減小，K值每增加20 MN/m3，隨著深度的增加，其彎矩減小的百分比越大，最大為0.73%，而抗滑樁嵌固段樁身的剪力先增大后減小，在滑面以下約1 m的位置變化百分比最大，為14.73%;地基系數K值的變化對抗滑樁樁身位移的影響較大，即隨著K值的增加，抗滑樁嵌固段樁身位移逐漸減小，且其減小速率逐漸減慢，K值每增加20 MN/m3，隨著深度的增加，其位移減小的百分比越大，抗滑樁嵌固段樁身位移減小的百分比大于受荷段，且在樁底附近達到最大，為19.41%。

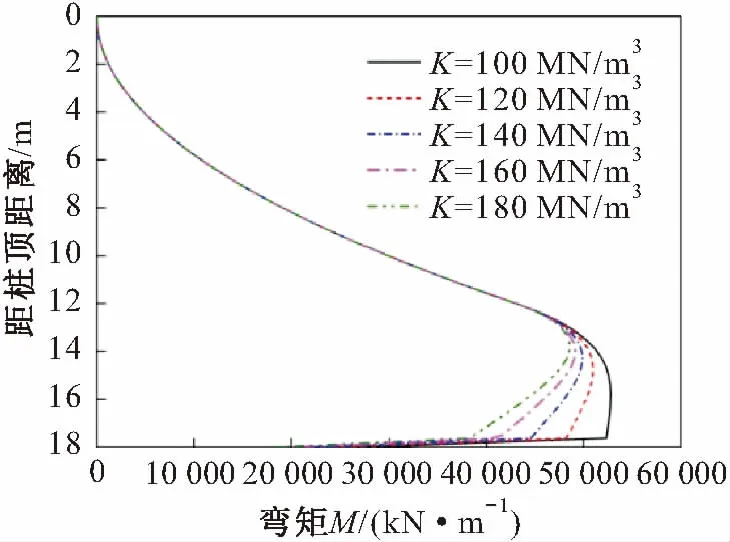
圖8 抗滑樁在不同地基系數下的彎矩圖(固定支承)Fig.8 Bending moment diagram under different foundation coefficients (fixed bearing)

圖9 抗滑樁在不同地基系數下的剪力圖(固定支承)Fig.9 Shear diagram under different foundation coefficients (fixed bearing)

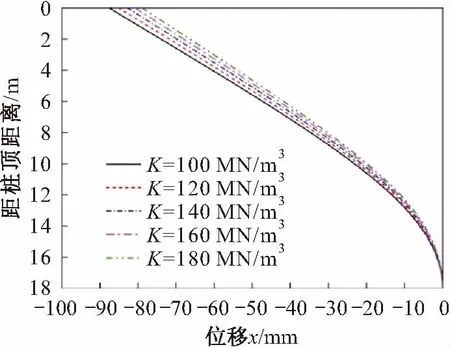
圖10 抗滑樁在不同地基系數下的位移圖(固定支承)Fig.10 Displacement diagram under different foundation coefficients (fixed bearing)

由圖8至圖10可見，對于樁底約束為固定支承的抗滑樁，當抗滑樁嵌固段長度一定時，地基系數K值的變化對抗滑樁嵌固段樁身彎矩M和剪力Q的影響較大，即隨著K值的增加，抗滑樁嵌固段樁身彎矩逐漸減小，K值每增加20 MN/m3，隨著深度的增加，其彎矩減小的百分比越大，最大為8.59%，而抗滑樁嵌固段樁身剪力也逐漸增大，且其增大速率逐漸減慢；地基系數K值的變化對抗滑樁樁身位移的影響較小，即隨著K值的增加，抗滑樁嵌固段樁身位移逐漸減小，且其減小速率逐漸減慢，K值每增加20 MN/m3，隨著深度的增加，其位移減小的百分比越大，最大為9.52%。

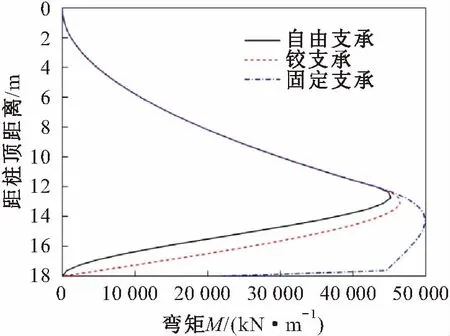
圖11 抗滑樁在不同樁底支承條件下的彎矩圖 (K=140 MN/m3)Fig.11 Bending moment diagram under different bearing conditions (K=140 MN/m3)

圖12 抗滑樁在不同樁底支承條件下的剪力圖 (K=140 MN/m3)Fig.12 Shear diagram under different bearing conditions (K=140 MN/m3)

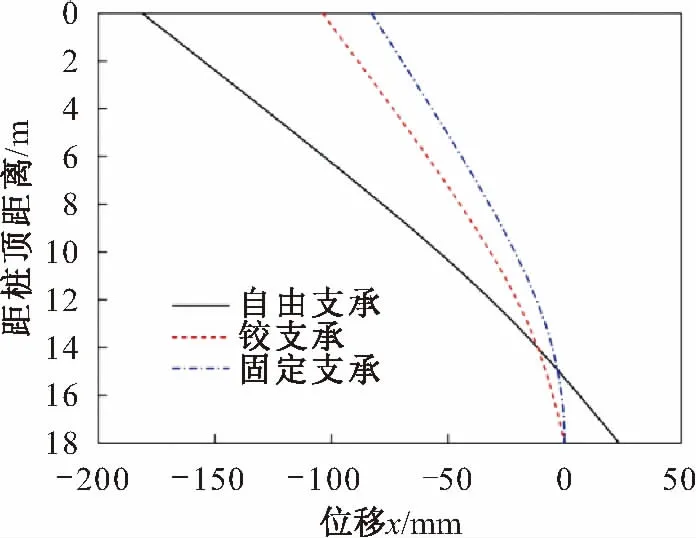
圖13 抗滑樁在不同樁底支承條件下的位移圖 (K=140 MN/m3)Fig.13 Displacement diagram under different bearing conditions (K=140 MN/m3)

由圖11至圖13可見，在3種支承條件下，抗滑樁受荷段樁身彎矩和剪力并無差別，但樁身位移差別較大，樁底約束為自由支承的抗滑樁樁身位移最大，鉸支承次之，樁底約束為固定支承的抗滑樁樁身位移最小；在抗滑樁嵌固段，隨著深度的增加，巖土錨固作用增強，不同樁底支承條件對抗滑樁樁身內力的影響逐漸明顯，樁底約束為固定支承的抗滑樁樁身彎矩最大、剪力最小，樁底約束為自由支承的抗滑樁樁身彎矩最小、位移最大。

綜上所述，通過對抗滑樁樁身內力和位移計算結果的分析可知，樁底支承條件形式不同，則得到的計算結果也不同。其中，固定支承計算得到的抗滑樁樁身彎矩最大，配筋設計時抗滑樁所需要的抗彎縱筋最多，而自由支承計算得到的抗滑樁樁身剪力最大，配筋設計時抗滑樁所需要的抗剪箍筋最多，這兩種支承形式所需要的鋼筋最多，會造成材料的浪費，增加工程投資；鉸支承計算得到的抗滑樁樁身內力和位移更接近實測值，配筋也較合理，也不會造成材料的浪費，因此樁底支承條件按鉸支承來進行抗滑樁設計更為合理。

4 結論與建議

(1) 本文采用傳統的抗滑樁內力計算方法“K”法推導了彈性抗滑樁受荷段和嵌固段樁身內力計算的理論公式，并在抗滑樁嵌固段樁身內力計算時考慮了樁底不同的支承條件。

(2) 當抗滑樁嵌固段長度一定時，嵌固段地基系數K值的變化對樁底約束為固定支承的抗滑樁樁身內力的影響最大，對樁底約束為自由支承和鉸支承的抗滑樁樁身內力的影響很小，因此在抗滑樁工程設計中應盡量避免抗滑樁樁底約束為固定支承的這種情況。

(3) 對于樁底約束為自由支承的抗滑樁，地基系數K值的變化對其樁身位移的影響最大，鉸支承次之，對樁底約束為固定支承的抗滑樁樁身位移的影響最小，因此對于樁身變形要求比較高的工程，對于地基系數K值的取值應更為精確，且應盡量選擇樁底約束為鉸支承的情況。

[1] 鐵道部第二勘測設計院.抗滑樁設計與計算[M].北京：中國鐵道出版社，1983.

[2] 王薇，徐志誠,鄧清祿.滑坡治理抗滑樁內力監測方法與數據處理[J].安全與環境工程,2010,17(2)：5-8.

[3] 宋英杰,陳文強,李長東.抗滑樁加固后邊坡穩定性評價與樁位優化研究進展[J].安全與環境工程,2016,23(5)：44-54.

[4] 吳恒立.計算推力樁的綜合剛度原理和雙參數法[M].2版.北京：人民交通出版社，2000.

[5] 高同玠.在有軟弱滑動帶時滑坡推力、樁身應力、樁前抗力的整體分析計算法[C]//滑坡文集(第四集).北京：中國鐵道出版社，1984.

[6] 陳廣峰，梁雅強.水平基床系數影響因素的探討[J].蘭州理工大學學報,2005,31(2)：116-119.

[7] 黃小鵬，楊樹寶，劉光華,等.嵌巖抗滑樁底端支承條件有限元分析[J].重慶交通大學學報(自然科學版),2011,30(1)：526-529.

[8] 戴自航.抗滑樁滑坡推力和樁前滑體抗力分布規律的研究[J].巖石力學與工程學報,2002,21(4):517-521.

[9] 楊濤,周德培,張俊云,等.抗滑樁滑坡推力分布形式的計算確定[J].巖土工程學報,2006,28(3):322-326.

[10]王敏澤.抗滑樁后滑坡推力分布定量分析[J].人民長江,2014,45(11):60-63.

[11]倪悅.半坡抗滑樁受力特性分析[D].重慶：重慶交通大學，2013.

[12]劉鴻文,林建興,曹曼玲.高等材料力學[M].北京：高等教育出版社，1985.

[13]佴磊,馬麗英,冷曦晨,等.滑坡治理中的抗滑樁設計[J].吉林大學學報(地球科學版),2002,32(2):162-165.

[14]陳靜瑜,趙煉恒,李亮,等.折線型滑面邊坡強度參數反演的極限分析上限法[J].中南大學學報(自然科學版),2015,46(2):638-644.

[15]張金華.巖土體抗剪強度參數反演及滑坡災害預測研究[D].重慶:重慶交通大學，2010:2-4.