基于局部密度自適應(yīng)度量的粗糙K-means聚類算法*

馬福民,逯瑞強(qiáng),張騰飛

(1.南京財(cái)經(jīng)大學(xué)信息工程學(xué)院,江蘇 南京 210023;2.南京郵電大學(xué)自動(dòng)化學(xué)院,江蘇 南京 210023)

1 引言

聚類分析是根據(jù)“物以類聚”的原理將物理或者抽象對(duì)象所組成的集合進(jìn)行分類的一種多元統(tǒng)計(jì)分析方法，己經(jīng)成為數(shù)據(jù)挖掘領(lǐng)域一個(gè)非常重要的分支，被廣泛應(yīng)用于機(jī)器學(xué)習(xí)、圖像分割等眾多領(lǐng)域。按照其特點(diǎn)，聚類算法大致可以分為五類：劃分方法、層次方法、密度方法、柵格方法和模型化方法[1]。K-means算法是最常見(jiàn)的劃分聚類方法之一，于1967年由Queen[2]首次提出，目前依然是眾多數(shù)據(jù)聚類分析任務(wù)首選的經(jīng)典算法。加拿大學(xué)者Lingras[3]在使用K-means算法對(duì)Web數(shù)據(jù)進(jìn)行挖掘分析時(shí)，針對(duì)傳統(tǒng)算法所存在的問(wèn)題，引入了粗糙集理論上、下近似的思想，提出了粗糙K-means聚類算法，在計(jì)算數(shù)據(jù)對(duì)象的歸屬關(guān)系時(shí)，不再是簡(jiǎn)單地用屬于或不屬于來(lái)表示，而是把確定屬于某一簇的對(duì)象歸屬到其相應(yīng)的下近似集中，不確定是否屬于該簇的對(duì)象歸屬到其相應(yīng)的邊界集中，因此，各個(gè)簇可以看作是由下近似集和邊界集兩部分組成。這種對(duì)聚類數(shù)據(jù)對(duì)象相對(duì)客觀的描述方法，在很大程度上提高了K-means聚類算法的精度。

粗糙K-means算法同其它任何的聚類分析算法一樣，算法的性能也依然受到初始參數(shù)、不確定性數(shù)據(jù)交叉重疊等因素的影響。為此，已經(jīng)有很多學(xué)者陸續(xù)提出了進(jìn)一步的改進(jìn)算法，從聚類結(jié)構(gòu)的角度來(lái)看，這些算法大致可以分為兩類[4]：

(1)粗糙K-means的擴(kuò)展算法。這類方法沒(méi)有改變聚類過(guò)程中簇內(nèi)的數(shù)據(jù)結(jié)構(gòu)，僅僅是在原有算法的基礎(chǔ)上，對(duì)初始參數(shù)、聚類指標(biāo)等進(jìn)行優(yōu)化。Peters[5]使用相對(duì)距離代替絕對(duì)距離，排除粗糙K-means算法中存在的受離群點(diǎn)干擾的問(wèn)題，并且結(jié)合遺傳算法對(duì)粗糙K-means算法的初始參數(shù)做了優(yōu)化[6]。

(2)粗糙K-means的衍生算法。這類算法可以認(rèn)為是對(duì)粗糙K-means算法的本質(zhì)提升，主要是針對(duì)均值迭代公式進(jìn)行修正。聚類對(duì)象之間的近似度量得以進(jìn)一步強(qiáng)化，如結(jié)合模糊集理論來(lái)構(gòu)建對(duì)象關(guān)系。文獻(xiàn)[7]發(fā)現(xiàn)了在粗糙K-means聚類結(jié)果中存在僅有邊界集非空的情況，并對(duì)粗糙K-means均值公式做了修正，對(duì)粗糙權(quán)值重新進(jìn)行了定義。文獻(xiàn)[8,9]介紹了粗糙模糊K-means聚類算法，這種方法使用了模糊隸屬度來(lái)反映簇間的差異性，提高了算法的精度。文獻(xiàn)[10]提出一種模糊粗糙K-means算法，對(duì)模糊隸屬度量進(jìn)行了修訂，將下近似集中數(shù)據(jù)對(duì)象的隸屬度設(shè)置為1，僅對(duì)邊界區(qū)域不確定的對(duì)象采用模糊度量。

現(xiàn)有的粗糙K-means衍生算法在構(gòu)造近似關(guān)系時(shí)大多僅關(guān)注單個(gè)數(shù)據(jù)對(duì)象與多個(gè)簇之間的差異性，而忽略了同一簇內(nèi)對(duì)象之間的區(qū)別，在同一個(gè)近似區(qū)域中使用統(tǒng)一的權(quán)值來(lái)衡量不同對(duì)象在均值迭代過(guò)程中的影響程度。然而，在一個(gè)簇的內(nèi)部，不同的數(shù)據(jù)對(duì)象點(diǎn)到均值中心的距離不同以及不同數(shù)據(jù)對(duì)象周圍的數(shù)據(jù)分布疏密程度等都將直接影響著聚類的結(jié)果。文獻(xiàn)[11]提出了一種對(duì)象點(diǎn)加權(quán)的方法，利用類似于方差統(tǒng)計(jì)的權(quán)值變形，區(qū)別簇內(nèi)對(duì)象的差異。文獻(xiàn)[12]利用統(tǒng)計(jì)對(duì)象點(diǎn)鄰域內(nèi)的距離總和來(lái)反映區(qū)域密度，提高了粗糙K-means算法的精度。文獻(xiàn)[13,14]認(rèn)為密度是一種空間特征，反映了樣本屬性的綜合趨勢(shì)和拓?fù)涞牟灰?guī)則構(gòu)型。文獻(xiàn)[15]綜合考慮了距離和密度的混合度量，但對(duì)于密度的度量方法是采用簡(jiǎn)單的鄰域范圍數(shù)據(jù)對(duì)象的數(shù)量統(tǒng)計(jì)，并沒(méi)有真正體現(xiàn)數(shù)據(jù)分布的疏密程度。這些方法利用各個(gè)空間特征構(gòu)建新的近似關(guān)系，但是大都缺乏對(duì)適應(yīng)性的考慮，不同的數(shù)據(jù)聚類可能對(duì)不同空間特征的敏感程度不同，基于空間特征的近似關(guān)系需要有綜合性的合理度量。

本文結(jié)合數(shù)據(jù)對(duì)象的不同分布對(duì)聚類結(jié)果的影響，提出一種局部密度自適應(yīng)度量的方法，并給出基于局部密度自適應(yīng)度量的粗糙K-means聚類算法，通過(guò)統(tǒng)計(jì)數(shù)據(jù)對(duì)象點(diǎn)與均值中心的距離以及鄰域內(nèi)數(shù)據(jù)分布的疏密程度，來(lái)描述簇內(nèi)數(shù)據(jù)對(duì)象分布的特點(diǎn)，靠近聚類中心且鄰域內(nèi)數(shù)據(jù)對(duì)象聚集程度高的數(shù)據(jù)點(diǎn)，將得到更高的自適應(yīng)迭代權(quán)值，從而加快聚類的收斂速度，并提高聚類的效果。最后，通過(guò)實(shí)例計(jì)算分析驗(yàn)證算法的有效性。

2 粗糙K-means聚類算法

粗糙K-means聚類算法是將粗糙集理論與K-means算法相結(jié)合，將具有不確定歸屬關(guān)系的數(shù)據(jù)對(duì)象劃入邊界區(qū)域，并使用不同的權(quán)值度量來(lái)降低邊界區(qū)域數(shù)據(jù)對(duì)象在迭代過(guò)程中的影響。算法實(shí)際上是將同一簇分為了兩個(gè)部分，即具有確定歸屬關(guān)系的下近似區(qū)域和具有不確定歸屬關(guān)系的邊界區(qū)域，通過(guò)區(qū)分下近似集和邊界集中數(shù)據(jù)對(duì)象的不同貢獻(xiàn)，一定程度上提高了模糊邊界的處理精度。

2.1 傳統(tǒng)的粗糙K-means聚類算法

根據(jù)Lingras所提出的粗糙K-means算法，聚類對(duì)象的處理具有以下三個(gè)特征[16]：

(1) 聚類對(duì)象最多只能確定地屬于某一個(gè)簇的下近似集；

(2) 聚類對(duì)象若不能確定地屬于某一個(gè)簇的下近似集，可同時(shí)屬于多個(gè)簇的上近似集；

(3) 每個(gè)簇的下近似集是它的上近似集的子集。

粗糙K-means算法與傳統(tǒng)K-means算法最大的區(qū)別主要體現(xiàn)在特征(2)中，將這些不適合硬劃分的數(shù)據(jù)對(duì)象，歸屬到多個(gè)簇共有的邊界集中。

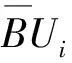
(1)

其中，wlow、wup分別為下近似集和上近似集的粗糙權(quán)值。

若每一個(gè)數(shù)據(jù)對(duì)象的類簇歸屬不再發(fā)生變化，說(shuō)明算法已經(jīng)收斂，算法終止；否則將新的Ci作為初始化中心，重新計(jì)算每一個(gè)數(shù)據(jù)對(duì)象到各個(gè)類簇中心的距離，并根據(jù)當(dāng)前的距離判斷到各個(gè)類簇的歸屬關(guān)系。

由于數(shù)據(jù)對(duì)象到各個(gè)類簇的劃分是依據(jù)其到類簇的均值中心Ci的距離，因此，均值中心的位置直接關(guān)系到聚類對(duì)象近似關(guān)系的判斷。從上述的計(jì)算過(guò)程不難看出，中心均值的迭代公式是影響最終聚類結(jié)果的關(guān)鍵因素。另外，粗糙K-means算法將簇分為下近似集和邊界集兩個(gè)部分，當(dāng)wup取值較小時(shí)，邊界對(duì)象在均值迭代計(jì)算過(guò)程中影響較小，降低了邊界區(qū)域數(shù)據(jù)對(duì)象的不確定性影響。

為評(píng)估粗糙K-means算法的收斂性以及聚類質(zhì)量，Lingras給出了如公式(2)所示的評(píng)估函數(shù)：

(2)

2.2 粗糙K-means的衍生算法

粗糙K-means聚類的衍生算法很多，其中比較經(jīng)典的是粗糙模糊K-means算法和模糊粗糙K-means算法。這兩種算法結(jié)合了模糊理論，以模糊隸屬度來(lái)表達(dá)聚類對(duì)象與各簇之間的從屬關(guān)系，表示對(duì)象以多大的程度歸入當(dāng)前簇。模糊隸屬度的表達(dá)式如下所示[8]：

(3)

其中，μij表達(dá)對(duì)象Xj關(guān)于簇Ui的隸屬度，m是模糊指數(shù)，dij表示Xj到均值中心Ci的距離，且模糊隸屬度滿足：

(4)

模糊隸屬度是一種簇間關(guān)系的表達(dá)，通過(guò)轉(zhuǎn)化比較簇間距離的比例關(guān)系，來(lái)反映對(duì)象與各簇的關(guān)聯(lián)程度。

粗糙模糊K-means算法將模糊隸屬度作為對(duì)象聚類的決策標(biāo)準(zhǔn)，將對(duì)象歸入隸屬程度最大的簇的下近似集；或者當(dāng)對(duì)象關(guān)于多個(gè)簇的隸屬程度相近時(shí)，則將對(duì)象歸入多個(gè)簇的上近似集。并且，算法對(duì)均值中心的迭代計(jì)算公式(1)進(jìn)行了改進(jìn)，如公式(5)所示[9]：

(5)

從均值計(jì)算公式(5)中可以看出，粗糙模糊K-means強(qiáng)調(diào)了對(duì)象在簇間和簇內(nèi)的差異度，與采用固定權(quán)值的粗糙K-means算法相比，其聚類過(guò)程對(duì)邊界的處理更加平滑。

模糊粗糙K-means算法則從另外一個(gè)角度對(duì)模糊隸屬度量公式進(jìn)行了改進(jìn)，即凡是在下近似集中的對(duì)象，隸屬度全部賦值為1，表示分配在下近似集中的對(duì)象絕對(duì)屬于當(dāng)前簇。模糊粗糙K-means算法還將均值中心的計(jì)算公式進(jìn)行了簡(jiǎn)化，省卻了粗糙權(quán)值，公式如下[10]：

(6)

其中，N′表示第i個(gè)簇當(dāng)中所包含的對(duì)象個(gè)數(shù)。

粗糙模糊K-means和模糊粗糙K-means算法一定程度上體現(xiàn)了不同的數(shù)據(jù)對(duì)象在計(jì)算均值中心時(shí)的差異性，但更多的是從對(duì)整個(gè)簇的度量角度出發(fā)，針對(duì)同一簇內(nèi)不同數(shù)據(jù)對(duì)象的不同分布及對(duì)聚類結(jié)果的影響考慮較少[17,18]，然而這些距離或局部密度分布卻對(duì)聚類結(jié)果有著不可忽略的影響。

3 基于局部密度自適應(yīng)度量的聚類算法

3.1 局部密度自適應(yīng)度量

從粗糙K-means及其衍生算法的實(shí)現(xiàn)原理，可以總結(jié)出粗糙K-means系列算法處理邊界模糊性問(wèn)題的特點(diǎn)：

(1) 將帶有不確定歸屬關(guān)系的聚類對(duì)象放在多個(gè)簇的共有邊界中；

(2) 距離均值中心越遠(yuǎn)的對(duì)象在迭代的過(guò)程中其權(quán)重越小；

(3) 聚類對(duì)象無(wú)論是在簇內(nèi)還是簇間，對(duì)聚類迭代過(guò)程及結(jié)果均有不同的影響。

文獻(xiàn)[15]對(duì)比分析了粗糙K-means算法、粗糙模糊K-means算法、模糊粗糙K-means算法在一個(gè)簇中不同數(shù)據(jù)分布的權(quán)值分配，如圖1～圖3所示，其中wlow=0.7，wup=0.3，m=2。

Figure 1 Weight distribution of rough K-means圖1 粗糙K-means算法的權(quán)值分配

Figure 2 Weight distribution of rough fuzzy K-means圖2 粗糙模糊K-means算法的權(quán)值分配

Figure 3 Weight distribution of fuzzy rough K-means圖3 模糊粗糙K-means算法的權(quán)值分配

可以看出，粗糙K-means的權(quán)值顯然比較生硬，只是簡(jiǎn)單地對(duì)同簇的對(duì)象權(quán)值二值化，并沒(méi)有體現(xiàn)出下近似集和邊界集內(nèi)部的差異性；粗糙模糊K-means的權(quán)值則顯得比較平滑，并且在很大程度上降低了邊界區(qū)域?qū)抵行牡挠绊懀牵捎谡瞻崮：`屬度量的原理，使得下近似集當(dāng)中的對(duì)象往往受到虛線部分的簇間影響；模糊粗糙K-means則對(duì)下近似集中的對(duì)象權(quán)重直接賦予1，表示下近似集確定屬于當(dāng)前簇，但是，依然沒(méi)有考慮下近似集對(duì)象因分布不均衡而產(chǎn)生的不同影響。

從上述分析不難看出，數(shù)據(jù)對(duì)象的權(quán)重系數(shù)應(yīng)當(dāng)由均值中心向邊界降低，并且越靠近邊界，下降應(yīng)越快。而且，權(quán)值的設(shè)置除了體現(xiàn)出與距離的關(guān)系，還應(yīng)和簇內(nèi)數(shù)據(jù)對(duì)象的聚集程度即空間分布有關(guān)。為了充分更好地描述數(shù)據(jù)對(duì)象的這種距離與空間分布，給出一種局部密度自適應(yīng)度量的方法。

局部密度自適應(yīng)度量的表達(dá)式如下：

(7)

其中，‖Xj-Ci‖表示對(duì)象Xj到所在簇的中心Ci的歐氏距離；|L(Xj)|ξ表示距離Xj為ξ的鄰域范圍內(nèi)數(shù)據(jù)對(duì)象的個(gè)數(shù)。

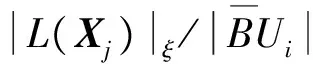
公式(7)的第一部分體現(xiàn)了數(shù)據(jù)對(duì)象點(diǎn)到均值中心的距離對(duì)權(quán)重系數(shù)的影響，可以看做是點(diǎn)到點(diǎn)的不同位置特征分布；第二部分則體現(xiàn)了數(shù)據(jù)對(duì)象點(diǎn)鄰域范圍內(nèi)局部的數(shù)據(jù)空間分布對(duì)權(quán)重系數(shù)的影響，可以看做是點(diǎn)到面的不同空間特征分布。整體而言，上述局部密度自適應(yīng)度量的表達(dá)式較好地體現(xiàn)了簇內(nèi)數(shù)據(jù)對(duì)象不同分布的空間特征，并較好地刻畫了不同空間分布的數(shù)據(jù)對(duì)象之間的差異性。

3.2 基于局部密度自適應(yīng)度量的聚類算法設(shè)計(jì)

結(jié)合上一節(jié)局部密度自適應(yīng)度量的方法，本節(jié)進(jìn)一步給出一種基于局部密度自適應(yīng)度量的粗糙K-means聚類算法RKM-LDAM(RoughK-means clustering based on Local Density Adaptive Measure)，算法流程如圖4所示。

Figure 4 Flow chart of algorithm圖4 算法流程圖

根據(jù)圖4所示的流程，RKM-LDAM算法的詳細(xì)描述如下所示：

算法1RKM-LDAM算法：基于局部密度自適應(yīng)度量的粗糙K-means聚類。

輸入：U：U={Xj|j=1,…,N}，對(duì)象數(shù)為N的數(shù)據(jù)集；

k：聚類簇的個(gè)數(shù)。

輸出：將數(shù)據(jù)對(duì)象集合U劃分為k個(gè)簇。

Step1參數(shù)設(shè)置與初始化，包括：

Ci：聚類均值中心，且i=1,…,k；wlow、wup：分別為下近似集和上近似集的相對(duì)粗糙權(quán)值系數(shù)；Δ：距離判斷閾值；ξ：局部密度統(tǒng)計(jì)范圍閾值。

Step2?Xj∈U，計(jì)算Xj到各均值中心Ci的距離dij(i=1,…,k)，統(tǒng)計(jì)Xj附近ξ范圍內(nèi)對(duì)象個(gè)數(shù)|L(Xj)|ξ；

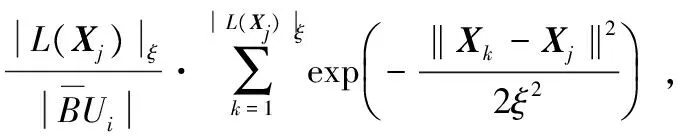
(8)

Step5根據(jù)公式(1)檢測(cè)結(jié)果是否收斂，若不收斂，返回Step 2重新進(jìn)行迭代聚類計(jì)算；否則，算法終止，輸出k個(gè)類簇。

就上述算法的時(shí)間復(fù)雜度而言，步驟2的復(fù)雜度為O(|U|2)，步驟3的復(fù)雜度為O(k|U|)，步驟4在最壞情況下為O(|U|2)，因此本文算法單次迭代計(jì)算的時(shí)間復(fù)雜度為O(|U|2)。

4 實(shí)驗(yàn)仿真與分析

為了驗(yàn)證算法有效性，采用本文基于密度自適應(yīng)度量的粗糙K-means算法(RKM-LDAM)對(duì)多個(gè)UCI數(shù)據(jù)集進(jìn)行聚類測(cè)試，并與典型的粗糙K-means算法RKM(RoughK-means)、模糊K-means算法FKM(FuzzyK-means)、粗糙模糊K-means算法RFKM(Rough FuzzyK-means)、模糊粗糙K-means算法FRKM(Fuzzy RoughK-means)在聚類精度和運(yùn)行速度方面進(jìn)行對(duì)比分析。

4.1 實(shí)驗(yàn)環(huán)境

本文選取了4個(gè)UCI數(shù)據(jù)集作為實(shí)驗(yàn)對(duì)象，分別是Iris、Wine、Fertility和Ionosphere。這4個(gè)UCI數(shù)據(jù)的一些信息和特征描述如下：

Iris是一個(gè)最常用的UCI數(shù)據(jù)集，包含了一些植物特征和鳶尾花分類之間的信息。該數(shù)據(jù)集包含150個(gè)樣本，每個(gè)樣本有4個(gè)條件屬性和1個(gè)決策屬性，其中決策屬性將數(shù)據(jù)分為3類。

Wine數(shù)據(jù)集主要是對(duì)同一區(qū)域的意大利葡萄酒的化學(xué)成分分析。數(shù)據(jù)集包含了178個(gè)樣本，每個(gè)樣本有13個(gè)屬性和1個(gè)決策屬性，其中決策屬性將數(shù)據(jù)分為3類。

Fertility記錄了生育能力和一些生理記錄之間的聯(lián)系。數(shù)據(jù)集包含了100個(gè)樣本，每個(gè)樣本有9個(gè)條件屬性和1個(gè)決策屬性，其中決策屬性將數(shù)據(jù)分為2類。

Ionosphere數(shù)據(jù)集通過(guò)分析電離層結(jié)構(gòu)來(lái)判斷電離層的好壞。數(shù)據(jù)集包含了351個(gè)樣本，每個(gè)樣本有34個(gè)條件屬性和1個(gè)決策屬性，其中決策屬性將數(shù)據(jù)集分為2類。

實(shí)驗(yàn)的計(jì)算機(jī)平臺(tái)使用英特爾酷睿i7(2.90 GHz)處理器，4 GB內(nèi)存，操作系統(tǒng)是Windows 7 SP1。

4.2 聚類效果分析

為了比較算法聚類效果，實(shí)驗(yàn)在聚類精度和運(yùn)行速度兩個(gè)方面對(duì)各個(gè)算法進(jìn)行對(duì)比分析。由于所選數(shù)據(jù)集均有較明確的分類決策，這里聚類精度是指對(duì)比原數(shù)據(jù)集的決策屬性值，被正確聚類的數(shù)據(jù)對(duì)象在數(shù)據(jù)集中所占的百分比，計(jì)算公式為：

(9)

為了便于比較不同算法的性能，實(shí)驗(yàn)過(guò)程中對(duì)同一數(shù)據(jù)集使用統(tǒng)一的初始聚類均值中心，對(duì)算法中多個(gè)參數(shù)的設(shè)置采用經(jīng)驗(yàn)選擇，由于個(gè)別的算法會(huì)涉及不同的參數(shù)，經(jīng)過(guò)測(cè)試，這些參數(shù)均選取較優(yōu)的組合，這里暫不考慮最優(yōu)參數(shù)的選取過(guò)程。

聚類參數(shù)的設(shè)置如表1所示。

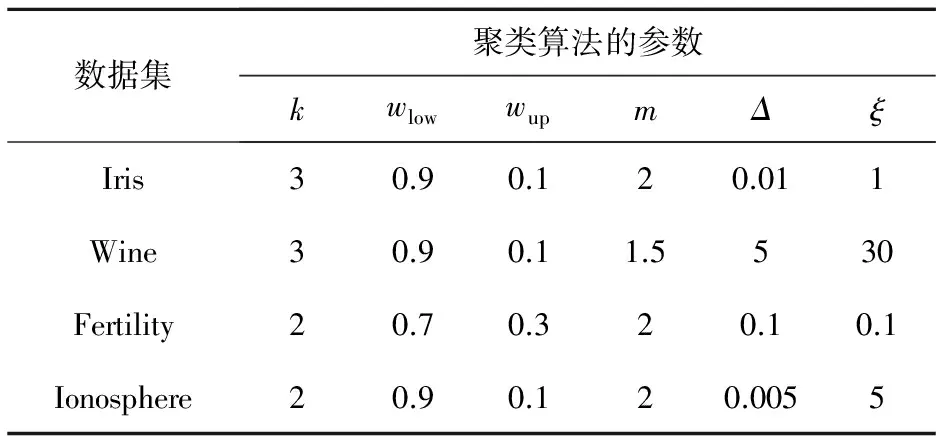
Table 1 Parameter settings for clustering algorithms

為了更為客觀地對(duì)各算法進(jìn)行對(duì)比分析，針對(duì)每一個(gè)數(shù)據(jù)集，每種算法均采用十字交叉驗(yàn)證，表2和表3分別記錄了各個(gè)聚類算法平均的精度和運(yùn)行時(shí)間，圖5和圖6直觀地反映了不同算法在各數(shù)據(jù)集中的聚類效果。

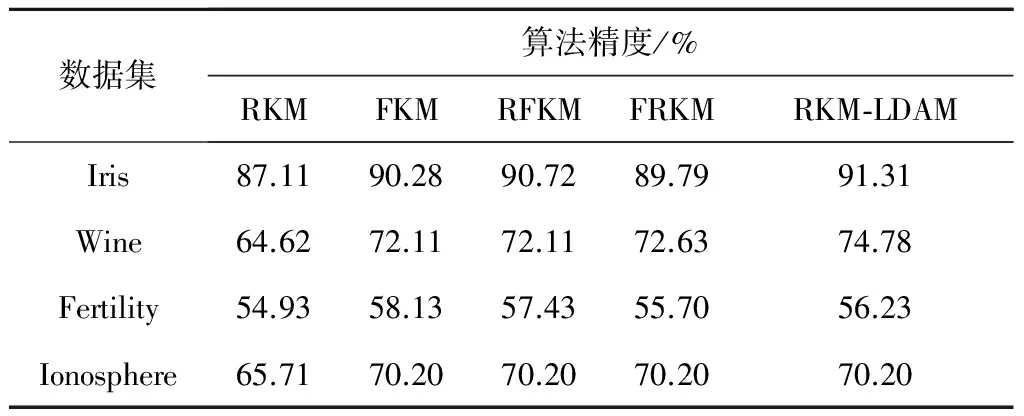
Table 2 Accuracy comparison of differentclustering algorithms on UCI data sets

Table 3 Computational time comparison ofdifferent clustering algorithms on UCI data sets

Figure 5 Accuracy comparison of different algorithms圖5 各算法聚類精度

Figure 6 Computational time of different algorithms圖6 各聚類算法運(yùn)行時(shí)間

從表2和圖5不難看出，本文設(shè)計(jì)的基于密度自適應(yīng)度量的粗糙K-means算法(RKM-LDAM)，有著不輸于其它算法的聚類性能，對(duì)Iris、Wine、Ionosphere三個(gè)數(shù)據(jù)集都達(dá)到了最高的聚類精度，尤其是對(duì)Iris和Wine兩個(gè)數(shù)據(jù)集的效果更好；僅僅對(duì)Fertility數(shù)據(jù)集的聚類精度稍低于采用模糊聚類FKM和RFKM方法的聚類結(jié)果。而由表3和圖6可以看出，除了Fertility數(shù)據(jù)集，本文所使用的RKM-LDAM算法的運(yùn)行速度都比較快，其中對(duì)Ionosphere數(shù)據(jù)集的聚類收斂速度更為突出，相對(duì)5種算法的平均耗時(shí)下降了15.87%。

綜合上述結(jié)果可以看出，基于局部密度自適應(yīng)度量的粗糙K-means算法(RKM-LDAM)，通過(guò)對(duì)聚類數(shù)據(jù)對(duì)象的空間特征進(jìn)行局部密度自適應(yīng)度量，更有利于提高聚類算法的性能，也驗(yàn)證了數(shù)據(jù)對(duì)象點(diǎn)在簇內(nèi)的不同分布會(huì)對(duì)聚類的結(jié)果產(chǎn)生一定的影響。

5 結(jié)束語(yǔ)

簇內(nèi)數(shù)據(jù)對(duì)象與均值中心的不同距離、鄰近范圍內(nèi)數(shù)據(jù)分布的疏密程度直接影響著聚類的精度與收斂速度。針對(duì)這一問(wèn)題，本文提出了一種基于局部密度自適應(yīng)度量的粗糙K-means聚類算法，在聚類的迭代計(jì)算過(guò)程中，通過(guò)對(duì)簇內(nèi)數(shù)據(jù)對(duì)象與均值中心的距離以及局部密度的自適應(yīng)度量，使得聚類結(jié)果簇內(nèi)相似程度更高、收斂速度更快。通過(guò)對(duì)多個(gè)UCI數(shù)據(jù)集進(jìn)行測(cè)試計(jì)算并與以往的多種算法進(jìn)行對(duì)比分析，說(shuō)明本文算法具有較好的聚類效果。

[1] Han Jia-wei, Kamber M. Data mining,concepts and techniques [M].3rd Edition. San Francisco:Morgan Kaufmann Publishers,2011.

[2] Queen M. Some methods for classification and analysis of multivariate observation[C]∥Proc of the 5th Berkeley Symposium on Mathematical Statistics and Probability,1967:218-297.

[3] Lingras P,West C.Interval set clustering of web users with roughk-means [J].Journal of Intelligent Information Systems,2004,23(1):5-16.

[4] Peters G,Crespo F,Lingras P,et al.Soft clustering-fuzzy and rough approaches and their extensions and derivatives [J].International Journal of Approximate Reasoning,2013,54(2):307-322.

[5] Peters G.Outliers in roughk-means clustering [C]∥Proc of International Conference on Pattern Recognition and Machine Intelligence,2005:702-707.

[6] Peters G,Lampart M.A partitive rough clustering algorithm [C]∥Proc of International Conference on Rough Sets and Current Trends in Computing,2006:657-666.

[7] Peters G.Some refinements of roughk-means clustering [J].Pattern Recognition,2006,39(8):1481-1491.

[8] Mitra S, Banka H, Pedrycz W.Rough fuzzy collaborative clustering [J].IEEE Transactions on Systems,Man,and Cybernetics,Part B:Cybernetics,2006,36(4):795-805.

[9] Mitra S,Banka H,Pedrycz W.Collaborative rough clustering [C]∥Proc of International Conference on Pattern Recognition and Machine Intelligence,2005:768-773.

[10] Hu Qing-hua,Yu Da-ren.An improved clustering algorithm for information granulation [C]∥Proc of International Conference on Fuzzy Systems and Knowledge Discovery,2005:494-504.

[11] Liu Bing,Xia Shi-xiong,Zhou Yong,et al.A sample-weighted possibilistic fuzzy clustering algorithm [J].Acta Electronica Sinica,2012,40(2):371-375.(in Chinese)

[12] Zheng Chao,Miao Duo-qian,Wang Rui-zhi.Improved roughK-means clustering algorithm with weight based on density [J].Computer Science,2009,36(3):220-222.(in Chinese)

[13] Liu Qi-liang,Deng Min,Shi Yan,et al.A density-based spatial clustering algorithm considering both spatial proximity and attribute similarity [J].Computers & Geosciences,2012,46:296-309.

[14] Azadeh A,Saberi M,Anvari M,et al.An adaptive network based fuzzy inference system-genetic algorithm clustering ensemble algorithm for performance assessment and improvement of conventional power plants [J].Expert Systems with Applications,2011,38(3):2224-2234.

[15] Zhang Teng-fei,Chen Long,Ma Fu-min.A modified roughc-means clustering algorithm based on hybrid imbalanced measure of distance and density [J].International Journal of Approximate Reasoning,2014,55(8):1805-1818.

[16] Lingras P,Peters G.Rough clustering [J].Data Mining and Knowledge Discovery,2011,1(1):64-72.

[17] Zhang Teng-fei,Chen Long,Li Yun.Roughk-means clustering based on unbalanced degree of cluster [J].Control and Decision,2013,28(10):1479-1484.(in Chinese)

[18] Zhang Teng-fei,Ma Fu-min.Improved rough k-means clustering algorithm based on weighted distance measure with Gaussian function [J].International Journal of Computer Mathematics,2017,94(4):663-675.

附中文參考文獻(xiàn)：

[11] 劉兵,夏士雄,周勇,等.基于樣本加權(quán)的可能性模糊聚類算法[J].電子學(xué)報(bào),2012,40(2):371-375.

[12] 鄭超,苗奪謙,王睿智.基于密度加權(quán)的粗糙K-均值聚類改進(jìn)算法[J].計(jì)算機(jī)科學(xué),2009,36(3):220-222.

[17] 張騰飛,陳龍,李云.基于簇內(nèi)不平衡度量的粗糙K-means聚類算法[J].控制與決策,2013,28(10):1479-1484.