解析大衍筮法及易卦的蓍占概率

孫 滌

一、邵康節的“加一倍法”

北宋的易學大家邵雍在易卦整體結構的探究上達到了超越前賢的高度，他制定的“伏羲六十四卦圓方圖”是一座巔峰。其為易卦排序所遵循的方法，歷來人稱“加一倍法”，然而對內中的機理和邏輯，尚無一致和妥帖的解說。比邵雍略晚的大儒程顥算是慧眼獨具，曾評述道：“堯夫之數，只是加一倍法。以此知《太玄》都不濟事。”他認為“加一倍法”要比揚雄的太玄數更高卓。邵雍聽了程顥這番“識貨”的話，驚而撫其背曰：“大哥，你恁聰明！”*蔡元定亦云：“康節之學，雖作用不同，而其實則伏羲所畫之卦也，明道所謂加一倍法也。”

可是“加一倍法”更深層次的奧義，前代幾乎無人述及的，是邵雍把六十四個易卦“加了一倍”，拓展成(26)2=(64)2，計有4096種變化。因為無論陰爻還是陽爻，又有可變與不可變之分。在此有必要先弄清楚，邵雍之“加一倍法”的真實含義不是簡單地乘二加倍，而是二乘方。

欲準確把握“加一倍法”的真意，尤其要在應用上避免偏誤，還得從解讀“大衍筮法”入手。由大衍筮法筮得的是四個隨機數：6、8、7、9，其中6和8代表陰爻(6為可變之陰爻，8為不可變陰爻)，9和7代表陽爻(9為可變之陽爻，7為不可變陽爻)。這就是說，同為陰爻，有6和8兩種可能，同為陽爻也有9和7兩種可能。如此，每一個卦的六條爻，又包含著26=64種變化。六十四個易卦總共有4096種變化。以三爻的坤卦為例，可以是666(全是可變陰爻)，也可以是888(全為不可變陰爻)，也可以是668、686、866、688、868、886，一共有23=8種變化。坤上坤下的六爻坤卦是兩個地卦的疊加，故有8×8=(23)2=64種變化。

在此之前，先來回顧一下人類思想史上的一個著名片段，為其佐證。引進新的解析工具和更新認知的觀念方法，對于易學的現代探索，有著非同尋常的意義。

二、“加一倍法”與二進制算法

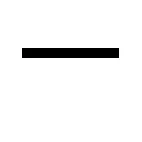
萊布尼茨在1703年4月1日讀到了在中國傳教的耶穌會士、法國人白晉*白晉(Joachim Bouvet)，1656年生于法國勒芒市，1686年被法皇路易十四選派為首批六名來華耶穌會士之一，于1688年抵達北京。作為親善大使，白晉直接溝通路易十四和康熙兩位君主，并深受器重，在《易經》探究上同康熙的切磋尤其頻繁。他通過與萊布尼茨的通信往返切磋，對二進制的開創有著(間接的)歷史性貢獻。雍正八年(1730)卒于北京。從北京寄給他的邵雍所制“伏羲六十四卦圓方圖”，頓時明白，“加一倍法”與他專研的二進制算法是高度契合的。白晉是當時屈指可數的漢學大師，他向萊布尼茨介紹了《周易》和八卦的系統。萊布尼茨認為陰、陽基本上就是他終身在探究的二進制的漢文明版本，并嘗試用二進制算法替八卦(三爻)和六十四個易卦作數字“身份認定”，從而排出了卦序的編號。

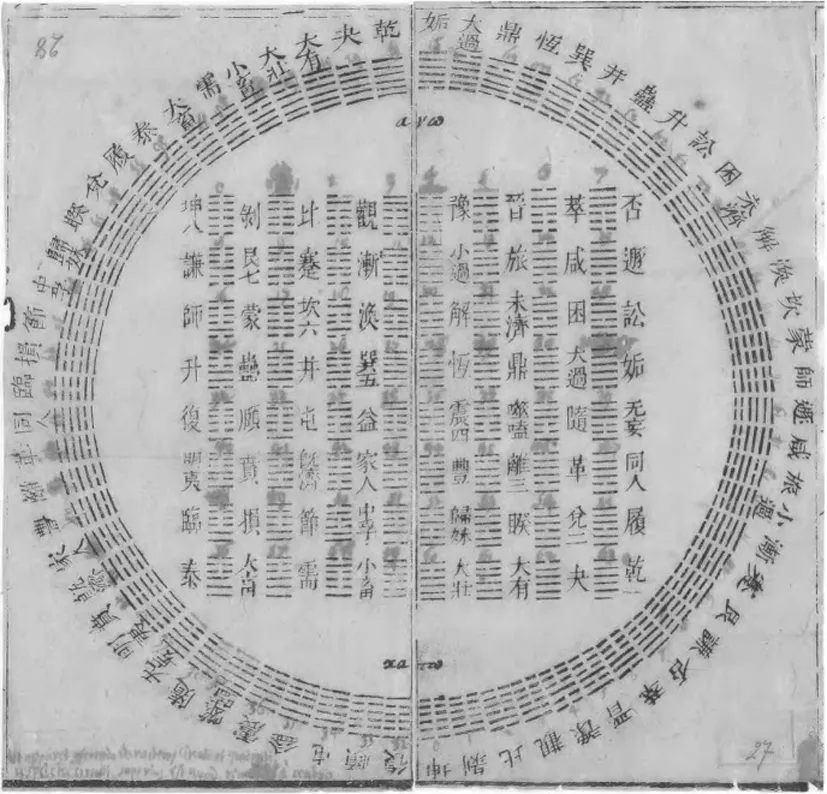
圖1

萊布尼茨專研和制定二進制算術的努力始于1670年代，他的相關論文則正式發表于1703年，而且終其一生都在不斷推進和改善。1697至1707年間，萊布尼茨和白晉通過書信往返，在《易經》探索上有長期的交流，其中至少有十五封書信現保存在德國圖林根的圖書館和漢諾威的萊氏文獻館。萊布尼茨懷著高度興趣研讀了白晉郵寄給他的易經《先天圖》(即由邵雍率先披露、托名伏羲的《伏羲六十四卦次序圖》和《伏羲六十四卦方位圖》)，并迅即給出了八個三爻卦和所有六十四個易卦的二進制編號(見圖1)*圖1為萊布尼茲所見到的邵雍“伏羲先天圓圖”和“伏羲先天方圖”，系由耶穌會士白晉隨信寄給他的原圖。該信1701年11月4日寫于北京，估計在1702年秋間送達德國漢諾威，但直到1703年4月1日方才為萊布尼茨讀到。萊氏閱后大喜過望，因為易卦結構明顯展現出其蘊涵的數理與自己專研了二十余年的二進制算法如出一轍。萊布尼茨于次日立即回復，詳細記錄了白晉有關這兩個系統具有同一性的發見以及自己的一些思考。隨后，萊氏于5月5日寄出他受到此圖啟發后修改完成的里程碑意義的論文，同年發表于法蘭西皇家學院學刊。該論文的初稿曾于兩年前投稿法蘭西皇家學院，由于缺乏應用實例和歷史依據，被質疑其可用性而遭到擱置。白晉提供的易經圖及應用佐證，幫助萊氏完成并成功發表了論文。。

在白晉提供的邵雍伏羲先天圖的啟發下，萊布尼茲從易卦的卦象得出了二進制編號，不禁為之驚喜。他在給白晉的回信中寫道：“我發現二進制數是二十年前。到今天我才發現……中國人在四千年前，已經了解到0與1的二元數學了。”而他發表于1703年的那篇劃時代論文的完整題目為《二進制算術的解釋——只用0和1符號，兼及它的一些應用，以及對中國古代伏羲圖像的破解》。足見萊布尼茨關于二進制的思考，與邵雍的象數和圖的確是息息相通的。

那么，萊布尼茲是怎樣用他首創的二進制算法來得到易卦的排序的？同“加一倍法”一般無二，萊氏以陽爻為1，陰爻為0，自上而下逐爻加倍來算出的。最簡單的,如坤卦的000000，排序為0(0×20+0×21+0×22+0×23+0×24+0×25=0)；乾卦111111的排序則是63(1×20+1×21+1×22+1×23+1×24+1×25=63)。 然而，既濟的010101，六條爻自上而下為0、1、0、1、0、1，排序又是多少呢？是0×20+1×21+0×22+1×23+0×24+1×25=42。如此可以很容易驗證，圖1里萊布尼茨給出的屯卦的010001和蒙卦的100010的排序分別是34和17，而否卦的111000和泰卦的000111排序則分別為7和56(結果見圖2)。

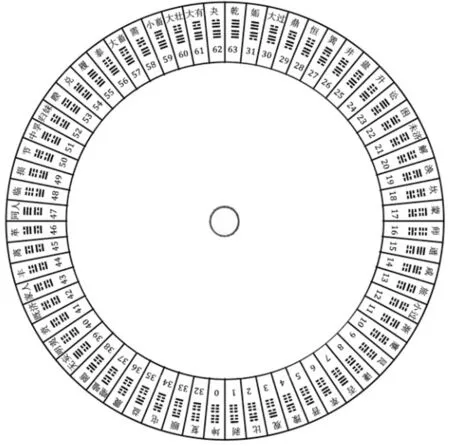
圖2

從坤卦0、剝卦1直到姤卦31逆時針排成圓圖的右半圈，然后從復卦32、頤卦33直至乾卦63，順時針排成圓形的左半圈。邵雍的伏羲先天圓圖實為“兩儀相逆”排列的結果*見圖1中萊布尼茨手寫的頁碼。27、28是倒著寫的，表明萊氏已深諳“兩儀相逆”之理。。非常有意思的是，經過圓心的連線聯接的兩卦成為一對，其排序之和必為63。這樣構成的32對卦里，只有8對(坤乾、小過中孚、坎離、大過頤，以及否泰、漸歸妹、未濟既濟、蠱隨)，在《周易》里原來就構成對卦，其余的24對都不是。這又是為什么呢？

再來看萊布尼茨對八個純卦(三爻)的排序：地0—山1—水2—風3—雷4—火5—澤6—天7，與邵雍在伏羲先天方圖里的排序(漢文數目字)正相逆。但是，兩種排序的相對位置則是相同的。若萊氏以陰爻為1、陽爻為0的話，排出的八卦序就幾乎跟邵雍完全一樣，將是地7—山6—水5—風4—雷3—火2—澤1—天0。生活在歐陸文明的人，單一起源的宇宙觀，猶太基督教的單一神主宰的范式是非常強有力的。萊布尼茨因而只能作另一選擇，即以陽爻為1，為至上的單一神所代表的宇宙最高的秩序和善；而以陰爻為0，表示混亂、渙散、虛無、不完善、甚至邪惡，總之，沒有結構可言。況且，天排在7，與西方固有的價值信仰并無出入，7在他們是個“圣數”，上帝造了六天的世界之后，第七天(星期天)是個休息日。

在萊氏排序里，山卦的排序為1。那么山1又是如何計算出來的呢？山卦的二進制代碼是100，按規范的二進制算法，其排序應當是0×20+0×21+1×22=4。萊布尼茨作出的“妥協”，是倒過來計算的，即自上而下逆向地“加一倍法”。也就是，以上爻位為初位，乘數為20=1，而以初爻位為最高的第三位，乘數為22=4計算出來的，結果序號才可能是1×20+0×21+0×22=1。問題是，倒過來看還是山卦嗎？它不就成了序號為1的雷卦001？同理，邵雍與萊氏排序中的雷4，按照規范的二進制算法，排序理當為雷1；而風3和澤6則分別應當是風6和澤3。換言之，八卦里面倒有一半排序發生了問題(見圖3)*該圖摘引自萊布尼茨于1703年發表于法國皇家學會學刊的二進制算法的論文，該論文在科學史上具有里程碑的意義。其中萊氏替被他稱作二進制算法源頭的中國遠古圣賢伏羲氏智慧的八卦，排了卦序。可以看到，萊氏所作的“妥協”，是他把卦象豎了起來，這在伏羲先天圖里是未曾有過的。結果，排為1的卦象究竟是山卦還是雷卦，于是含混起來(排序為3、4、6的卦象也是如此)。這個妥協帶來的含混產生了一系列后果，引致各種誤導。譬如，對太極圖里八卦的方位解讀問題。這里討論的自下而上與自上而下的差別，在八卦方位的環圖中，則是卦象究竟應該從外向環心看，還是從里朝環周看？對于萊氏豎著的卦象，問題卻變為卦象應該是從右到左，還是從左到右來看？。

圖3

這個問題蔓延到全部的六十四個易卦。譬如，否卦111000的排序應當是7(萊布尼茨的)，還是56(二進制數值法的)？與否卦成對的泰卦，排序究竟是7還是56？再以《周易》里的屯卦3—蒙卦4為例分析，萊氏及邵雍的排序，是屯卦34—蒙卦17，而在正規的二進制數值排序里，理應為屯卦17—蒙卦34！

這個困擾的肇因，絕不僅僅是簡單的算法技術問題，而是思考觀察的分析框架所致，背后有著文化和觀念的深厚積淀。萊布尼茨受此困擾，放棄了繼續深入挖掘。但是誰又想得到，這個問題竟得拖延三百余年，到今天才來解答呢？筆者將在另處，以“易學的現代詮釋”、“易卦結構與二進制的關系”等為題，展開深入辨析。

三、大衍筮法辨析

大衍筮法又稱揲蓍法、蓍占，或直接稱作周易占法，是載入《周易》原文的唯一筮法。歷朝歷代的易學家們口授心傳的依據，是《易傳·系辭》里的一段原文(《大衍之數五十》章及原注)*《易傳·系辭上》“大衍之數五十”章：“大衍之數五十，其用四十有九。分而為二以象兩，掛一以象三，揲之以四以象四時，歸奇于扐以象閏，五歲再閏故再扐而后掛。天數五，地數五，五位相得而各有合。天數二十有五，地數三十。凡天地之數五十有五，此所以成變化而行鬼神也。乾之策二百一十有六，坤之策百四十有四，凡三百有六十，當期之日。二篇之策萬有一千五百二十，當萬物之數也。是故四營而成易，十有八變而成卦，八卦而小成，引而伸之，觸類而長之，天下之能事畢矣。”。

筮占之“筮”，從竹從巫，“竹”代表草木，“巫”代表占卜。筮是用植物進行的預測，卜則是用動物做的預測。蓍占以蓍草為工具來指導“風險決策”，而卜則以龜甲、獸骨作為工具。《說文》有曰“筮，易卦用蓍也”，反映了西周時代就很流行的蓍筮文化。蓍占在早期是與龜卜并重的。《周易》大衍筮法得到重視，得以廣泛流傳和使用，與孔子及其門人作《易傳》并推崇蓍占有很大的關系，龜卜的方法漸漸失傳了。

圖4

筮占所用的道具是蓍草，一種長于西伯利亞和中國北方的多年生直立篙類植物。河南淮陽的伏羲太昊陵有蓍草園，但蓍草只生于那個園地的說法，并不確實。筮占是用50莖經過香薰的、長約尺許的干蓍草來進行的占卜，因其方法基于“大衍之數”，又被稱為“大衍筮法”。本質上，筮占是借“植物靈性”來“溝通天意”的(圖4)。

大衍筮法是八卦系統的四象筮法，得到的6、7、8、9四個數，6為可變之陰爻，9為可變之陽爻；7為不可變之陽爻，8為不可變之陰爻。這里的“可變”有待變之意，陰陽轉換——6待變為7，9待變為8。

就其實質而言，大衍筮法的過程是一個“隨機發生器”。問題在于，得到6、7、8、9這四個隨機數的概率分別是多少呢？下文的分析推導得出結論：同為陰爻，得到可變陰爻6的概率是1/16，得到不可變陰爻8的概率則為7/16；同為陽爻，得到可變陽爻9和不可變陽爻7的概率，分別是3/16和5/16*邵雍曰：“大衍之數，其算法之原乎？是以算數之起，不過乎方圓曲直也。乘數，生數也。除數，消數也。算法雖多，不出乎此矣。”(邵雍著，黃畿注，衛紹生校理：《皇極經世書》卷七上《觀物外篇上·河圖天地全數第一》，鄭州：中州古籍出版社，1993年，第311頁)沈括《夢溪筆談》卷七《象數一》：“《洪范》‘五行’數，自一至五。先儒謂之此‘五行生數’，各益以土數，以為‘成數’。以謂五行非土不成，故水生一而成六，火生二而成七，木生三而成八，金生四而成九，土生五而成十，合之為五十有五。唯《黃帝素問》：‘土生數五，成數亦五。’蓋水、火、木、金皆待土而成，土更無所待，故止一五而已。畫而為圖，其理可見。為之圖者，設木于東，設金于西，火居南，水居北，土居中央。四方自為生數，各并中央之土，以為成數。土自居其位，更無所并，自然止有五數，蓋土不須更待土而成也。合五行之數為五十，則大衍之數也。此亦有理。揲蓍之法：四十九蓍，聚之則一，而四十九隱于一中；散之則四十九，而一隱于四十九中。一者，道也。謂之無，則一在；謂之有，則不可取。四十九者，用也。靜則歸于一，動則惟睹其用，一在其間而不可取。此所謂‘大衍之數五十，其用四十有九’。”(沈括撰，胡道靜校注：《新校正夢溪筆談》，北京：中華書局，1957年，第78頁)。

大衍筮法產生的隨機結果，不加細辨的話，很容易誤以為得到這四個數的幾率是相等的，均為1/4。或者注意到了大衍筮法生成一爻需經過“三變”，三個階段的組合之后，得到6、7、8、9四個數的概率分別為1/8、3/8、3/8、1/8。雖說這幾種替代大衍筮法的簡化辦法，得到陰爻和陽爻(可變+不可變的)的概率，都還是各半(1/2)，然而其間微妙的變化，可以導致非常懸殊的結果。

厘清大衍筮法獲得6、7、8、9四個數的(隨機)準確概率，非常之有必要。畢竟，在《易傳》里得到奠基的卦辭、象辭、爻辭，以及各家的詮釋，所依據的都是大衍筮法的蓍占結果*諸多占卦預測的方法里，大衍筮法始終占據著主導地位。《左傳》、《國語》中記載的二十多則先秦筮案均為大衍筮案。后世以預測精確著稱的管輅、郭璞等高人所用的無不是大衍筮法，北宋的陳摶和邵雍用的也都是大衍筮法。近代如易學大家尚秉和先生的《筮案輯存》，數十則案例無一不是大衍筮案。。不嚴格按照大衍筮法生成爻和卦的概率，會對易卦的詮釋造成很大的偏誤。其他的概率，包括變通簡化方法得到的，如果不作相應的調整，很可能導致謬以千里的解卦結論和估測判斷。

歷來對大衍筮法產生的隨機結果有種種偏誤的理解，并不奇怪。大衍筮法的過程莊嚴繁瑣，不只令現代人感到茫然，古人也一定覺得很撓頭。朱熹不愧為不世出的大學者，他經過執著精細的研析，暗示出了6、7、8、9四個數，即可變之陰爻、不可變之陽爻、不可變之陰爻、可變之陽爻的得到概率是不平衡的，即所謂“可變之爻常少而不可變之爻常多”的道理*朱熹曰：“六爻皆不變，占本卦彖辭。”(朱熹撰，蘇勇校注：《周易本義》附錄二《易學啟蒙·考變占》，北京：北京大學出版社，1992年，第234頁)他又認為，“有天地自然之易，有伏羲之易，有文王周公之易，有孔子之易。自伏羲以上，皆無文字，只有圖畫，最宜深玩，可見作《易》本原精微之意。文王以下，方有文字，即今之《周易》。然讀者亦宜各就本文消息，不可便以孔子之說為文王之說也”(朱熹撰，蘇勇校注：《周易本義》附錄一《周易本義附圖·卦變圖》，第204頁)。而弄明白“伏羲卦象”要比讀懂《周易》通行文本更為重要。他說：“必欲知圣人作《易》之本，則當考伏羲之畫；若只欲知今《易》書文義，則但求之文王之經、孔子之傳足矣。兩者初不相妨，而亦不可以相雜。”。

在其名著《周易本義》卷首《筮儀》篇中，朱熹對大衍筮法的過程有相當詳盡的描述和注解。他說，四個數的概率之所以不平衡，是因為大衍筮法過程的端始，“取其一策，反于柜中”——“但用四十九蓍耳”，即大衍之數50，用的是49根蓍草的緣故*大衍筮法用49根蓍草，因此變化非常豐富奇譎。設若“取其二策，反于柜中”，即用的是48根蓍草的話，變化就要簡單得多，在那種情況下得到6、7、8、9四個隨機數的概率才是1∶3∶3∶1。。

第一變，“掛一”之后，隨機分成兩刻的蓍草剩下48莖。從每一群蓍草里分別取走4莖的整倍數后，再剔除其余數——或1或2或3或4莖，剩下了44莖或40莖。在第二變“掛一”之后，分別成了43莖或39莖。“歸奇”即剔除余數(3或7)后，從43莖剩下的是40莖或36莖，概率各半；從39莖則剩下36莖或32莖，概率也是相等的。然后是第三變，“掛一”之后則成了39莖、35莖或31莖。“歸奇”即剔除余數(3或7)后，從39莖剩下36莖或32莖，從35莖剩下32莖或28莖，從31莖則剩下28莖或24莖，概率也是各占其半。以朱熹的話來講，是“奇耦各得四之二焉”(3=1+2或2+1；7=3+4或4+3，各在四種可能性里占了兩種)。

然而其中的奧妙，是第一變所得到的“奇耦”，是否也“各得四之二焉”呢？非也。其關鍵就在于“但用四十九蓍耳”。

三變之后所剩下的24莖、28莖、32莖、36莖蓍草的4的整倍數，就是6、7、8、9(扐數)。得到6、7、8、9的概率，結果分別為1/16、5/16、7/16、3/16，其中得到7的概率是5/16=1/16+1/16+3/16；得到8的概率是7/16=1/16+3/16+3/16。

第一變在概率上的變化，導致了6、7、8、9隨機結果的比例是1∶5∶7∶3，而非4∶4∶4∶4。同樣的，2∶6∶6∶2也不準確*設若“存體”的蓍草莖數不是1，而是2的話，那么產生6、7、8、9這四個隨機數的概率分布將為八分之1∶3∶3∶1。這個概率分布是自唐代以來民間所習用的“搖錢筮法”等簡化方法產生的結果。作者把各個可能的“存體”數為初始值的大衍筮法的結果列表如下。假設：1.“存二”(50策蓍草里先取出2策不用)，得到四種爻的概率是多少？2.“存0”，即從50策蓍草先取出0策不用的話，又是怎樣的結果？3.“存三”，即從50策蓍草先取出3策不用的話，又是如何的呢？結果如下表所列：。這個道理，用概率分析的工具“決策樹”(三個階段)來描述，應當能一目了然(見附錄二)。

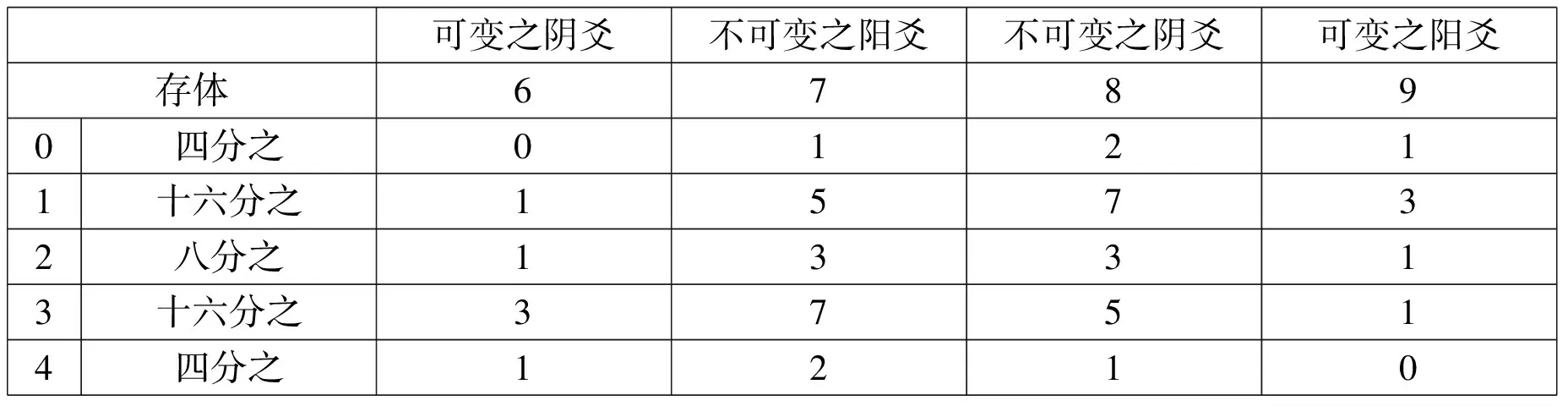
可變之陰爻不可變之陽爻不可變之陰爻可變之陽爻存體67890四分之01211十六分之15732八分之13313十六分之37514四分之1210

不過要做出一個簡單的隨機發生器來精確模擬“大衍筮法”的概率，卻有點復雜。由于世界上不存在正十六面體，無從設計出一個簡單的“骰子”，來隨機地獲得概率為1/16、3/16、5/16和7/16的四個隨機結果。作為替代，筆者建議的辦法，是用兩枚錢幣(fair coin)進行兩次拋擲，從而得到一條爻。其隨機概率可以列表如圖6。重復六遍，結果得到六條爻，便構成一個六爻易卦(圖5)。

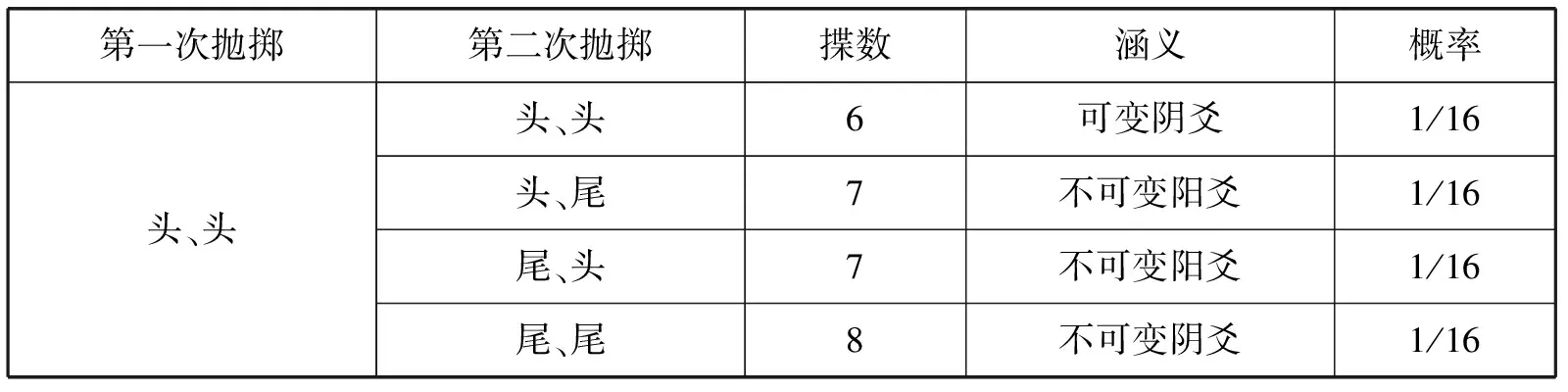
第一次拋擲第二次拋擲揲數涵義概率頭、頭頭、頭6可變陰爻1/16頭、尾7不可變陽爻1/16尾、頭7不可變陽爻1/16尾、尾8不可變陰爻1/16

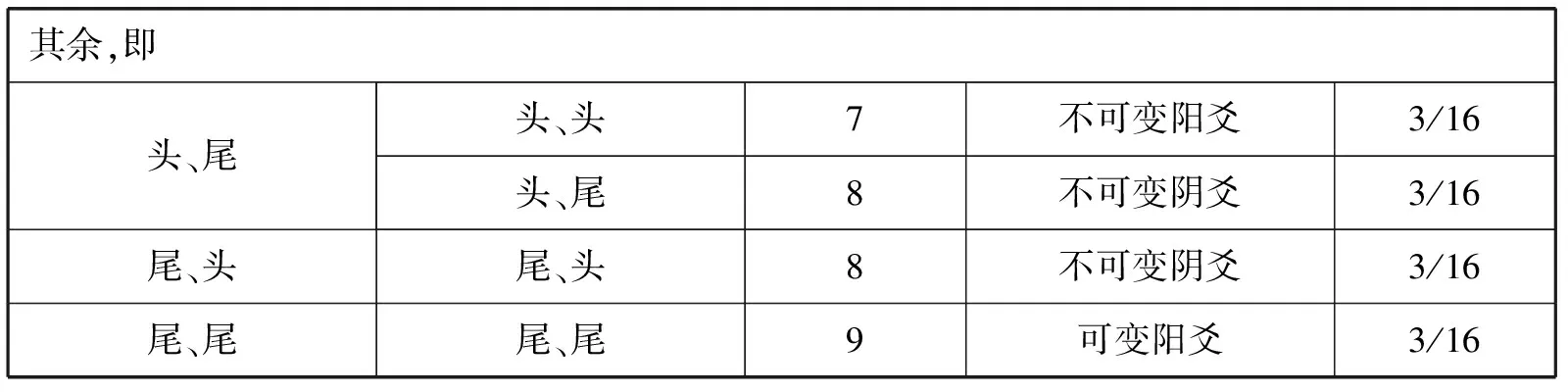
其余，即頭、尾頭、頭7不可變陽爻3/16頭、尾8不可變陰爻3/16尾、頭尾、頭8不可變陰爻3/16尾、尾尾、尾9可變陽爻3/16

圖5

由此得到的易卦，不但知道其為何卦，而且能很清晰地明白每一條爻是可變的還是不可變的。聯系《易經》、《易傳》對易卦的詮釋，對所得之卦的解釋才有可能做到精準。

四、由大衍筮法得到的易卦概率

那么，大衍筮法得到每個易卦的概率又是如何來計算的呢？以最簡單的純陰坤卦和純陽乾卦為例來說明。坤卦的六條陰爻，每條爻可以是可變的6或不可變的8，所以共有64種(2的六次方)變化來構成坤卦。六條爻皆為不可變(888888，數字從右至左代表初爻到上爻)的坤卦概率(7/16的六次方)，是六爻皆為可變(666666)的坤卦概率(1/16的六次方)的117649倍(7的六次方)。同理，同為六陽的乾卦，僅一條可變陽爻的乾卦977777(5/16的五次方×3/16)的概率是有四條可變陽爻的乾卦799997(5/16的二次方×3/16的四次方)的12.1倍。

大衍筮法生成每條爻是獨立生成的，三變成一爻、重復六遍成一卦，因此，每爻生成的概率相互獨立，與所在的爻位無關。例如，不可變陰爻8無論是在二爻位、五爻位，或任何爻位，概率都是7/16；可變陽爻9無論在哪個爻位，概率也都等于3/16。所以成卦的概率只決定于陰爻條數和陽爻條數(加起來為6)，及其可變性或不可變性。簡單地說，取決于n個6或8，與(6-n)個9或7的組合。因而計算卦的概率用的也是組合，而非排列方法。

以坤卦來說，它的64種變化只有7種獨立的概率，分別是n條(n=0、1、2、3、4、5、或6)可變陰爻的概率(1/16)乘以(6-n)條不可變陰爻的概率(7/16)，加權后成卦的概率為0.015625。以乾卦而言，也只有7種獨立的概率，分別是m條(m=0、1、2、3、4、5、或6)可變陽爻的概率(3/16)乘以(6-m)6條不可變陽爻的概率(5/16)，加權后成卦的概率也是0.015625(見圖6)。

1.5625%即1/64，說明在邵雍的“加一倍法”，得到所有的64個易卦的概率依然相等，即等概的。而每卦的構成盡管有64種變化，總共642=4096種變化，不過獨立概率的數目卻少得多。計算的結果表明，獨立概率總共才84個(詳見附錄二，完整的易卦概率表)。

“附錄二”的易卦概率表，是從陽爻的角度來對易卦分類，從而計算出各類卦的概率表。所有的64個卦，概率都是1/64，即1.56%。但是，1.56%的概率是如何分布為可變或不可變陽爻，可變或不可變陰爻的具體組合，則是大不相同的。

以三陽類的泰卦為例，它的三條陽爻可以有4種組合(0、1、2或3條可變陽爻結合相應的3、2、1或0條不可變陽爻)，它的三條陰爻也有4種組合(0、1、2或3條可變陰爻結合相應的3、2、1或0條不可變陰爻)。所以，構成泰卦的64種變化僅有4×4=16個獨立概率。這16個獨立概率適用于所有20個三陽類卦，這就是說，構成三陰類卦的1280種變化(64×20)里只有16個獨立的概率。譬如，688997的泰卦甲和868799的泰卦乙，概率是相等的，是(1×72×32×5)/166=0.000131428，故概率為0.01314%。這是因為，兩者都是由一條可變陰爻+兩條不可變陰爻+兩條可變陽爻+一條不可變陽爻來構成的。有同樣概率的泰卦共有9種變化。三陽卦類有20個，所以共有1280種變化(64×20)的三陽類卦，概率合起來是0.015625×20=31.25%(見圖7)。

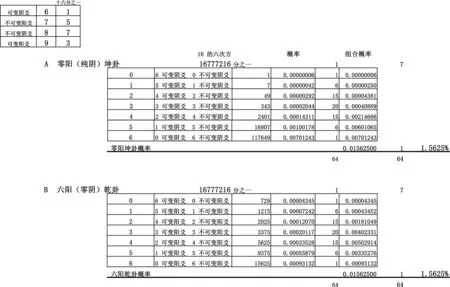
圖6

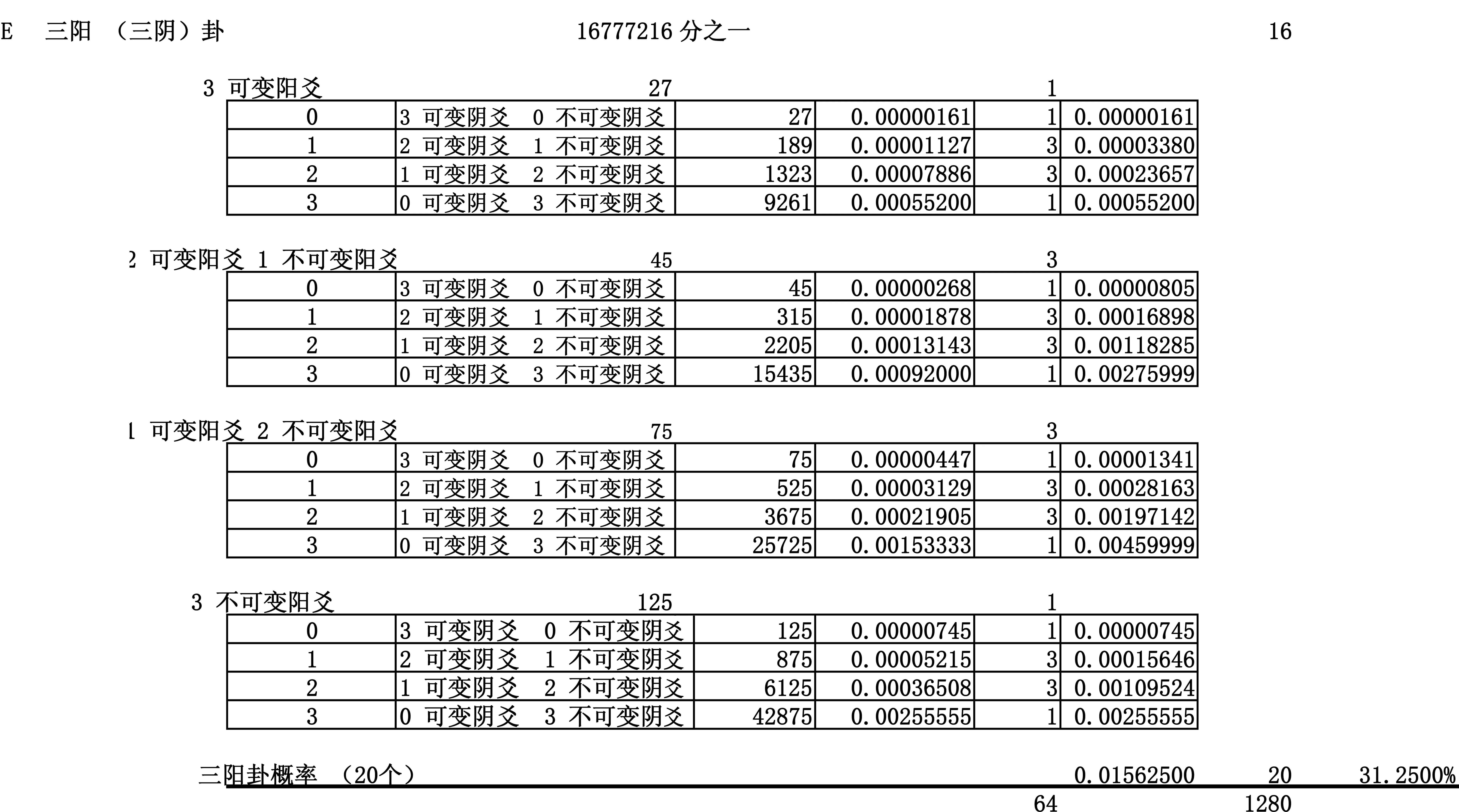
圖7

我們也可以從另外一個角度切入，來計算和運用附錄三的概率表。既然每個易卦都是兩個三爻純卦的疊加，另一個方法脈絡更單純、更易于理解，就是計算8個純卦的概率，然后相乘而成為64卦(詳見圖8)。

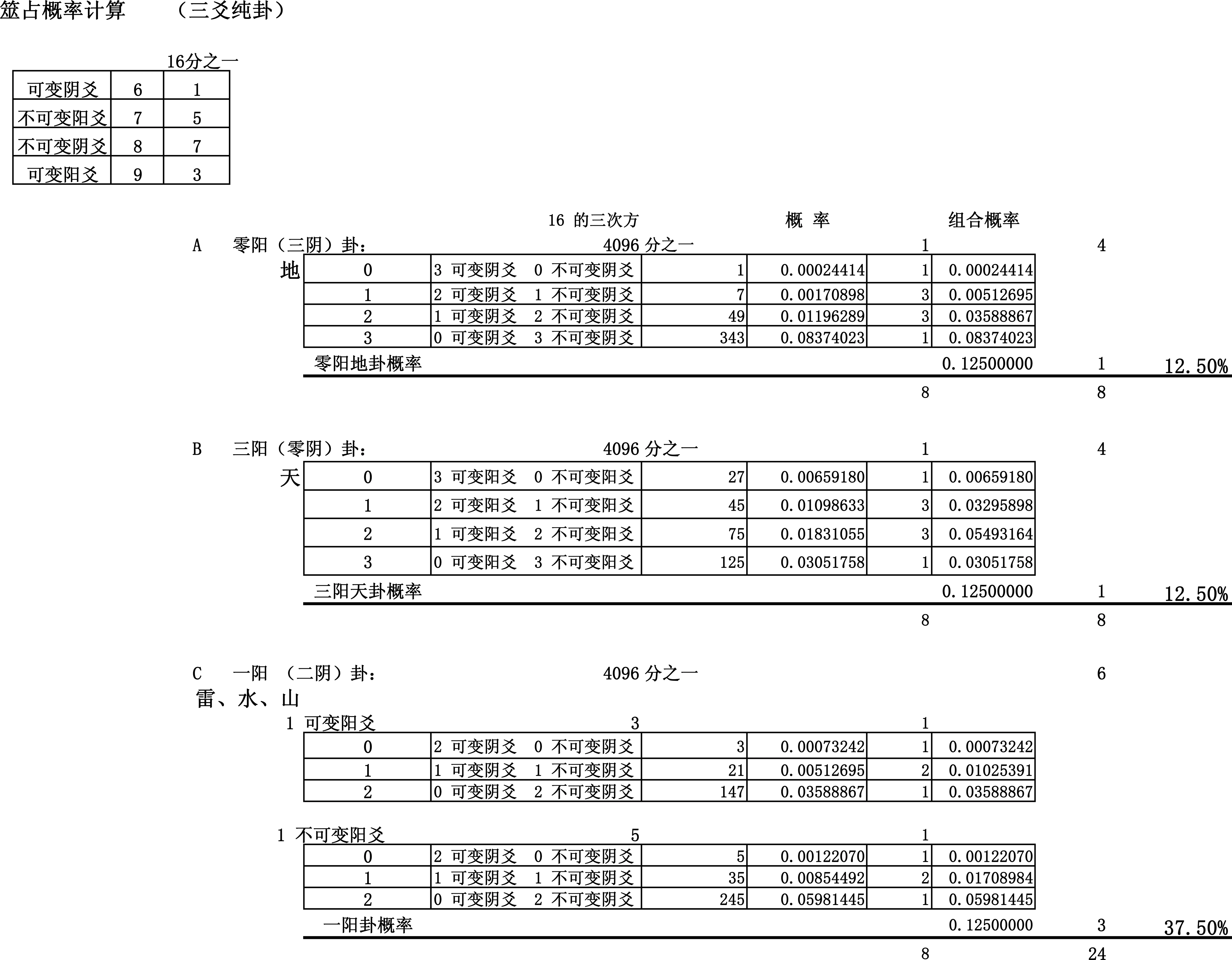
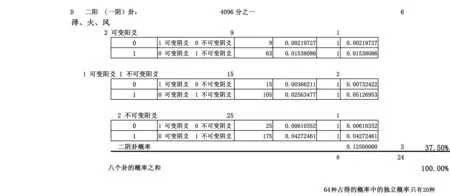
圖8

八卦可分四類：A零陽卦——地；B三陽卦——天；C一陽卦——雷、水、山；D二陽卦——澤、火、風。各卦的概率均為12.5%，也就是1/8。一陽、二陽類各有三個，所以一陽類、二陽類的概率，各為37.5%。四類的概率加總當然是100%。

據此不難明白，筮占獲得一個易卦(所謂“起卦”)，可以有64種變化，其中獨立的概率僅20個。用上文里舉過的例子，泰卦甲688997和泰卦乙868799來驗證。地天泰卦，甲的上體地卦688，乙的上體地卦868，都是三條陰爻，一條可變兩條不可變，概率同為0.011962891；甲的下體天卦997，乙的下體天卦799，三條陽爻里也都是兩條可變一條不可變，概率同樣都是0.010986328。兩者的乘積為0.000131428，同上面計算的結果是一樣的。也就是說，泰卦甲和泰卦乙的概率都是0.01314%。

邵雍的“加一倍法”有4096種變化，即六十四個易卦，每卦各有64種變化。計算分析的結果表明，其獨立的概率才84個。從附錄三的概率表，我們很容易加總起來得出；在圖8里也可以計算得到。八卦(三爻)的變化“加一倍”即二次方是64種，其獨立的概率僅20種。那么兩個八卦疊加之后，獨立概率又是幾何？也是84種。讀者不妨排出一個20×20的矩陣，400個乘積歸并之后，剩下的不同概率值(distinct values)，也正好是84個。

從實用的角度來講，不必太過精確。于是六十四個易卦，得到每卦的概率為1.56%。其中零陽卦1個、一陽卦6個、二陽卦15個、三陽卦20個、四陽卦15個、五陰卦6個、六陽卦1個。這七個類別的概率，分別為1.56%、9.36%、23.4%、31.36%、23.4%、9.36%、1.56%。

通過辨析大衍筮法，得以知道蓍占的結果，陰爻和陽儀——可變及不可變——的不同組合的準確概率，從而了解占得一卦的各種變形的機會有多少，占得的卦又將作何變化，用易學術語來講，是得到“之卦”的機會又是多少。在此“起卦”正確的基礎上，才能夠解卦，問兇吉、知得失，才有可能順應“道”或“天意”，從而順勢利導地趨利避害。

附錄一：三階段決策樹

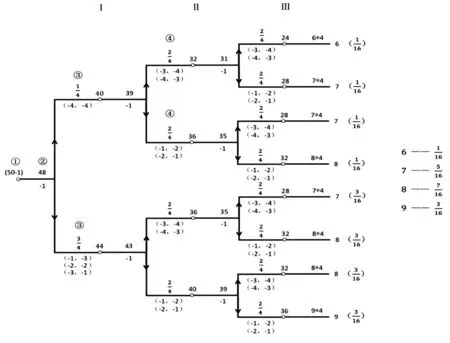
注解：①“存體”(50莖蓍草里先取出1莖不用)；②“掛一”(再拿走1莖)后把“致用”的48莖蓍草分作兩群(“分二”)；③按“扐”(“揲四”即以4莖為一簇)，取走核定的余數(“歸奇”)。此第一變(I)，余下40莖的概率為四分之一，余下44莖的概率則為四分之三；④重復②、③成第二變(II)。“掛一”和“歸奇”之后，分別剩下43莖或39莖。即剔除余數(3或7)后，從43莖剩下的是40莖或36莖，概率各半，從39莖剩下的是32莖或36莖，概率都是各半。再重復②③④成第三變(III)，則剩下24、36、28、32莖，概率分別為十六分之一、十六分之三、十六分之一(或三)、十六分之三(或一)。結果是，得到6、7、8、9(四的整除數)的概率，歸并起來，分別為1/16、5/16、7/16和3/16。

附錄二：易卦成卦概率表(大衍筮法引入可變和不可變爻后)

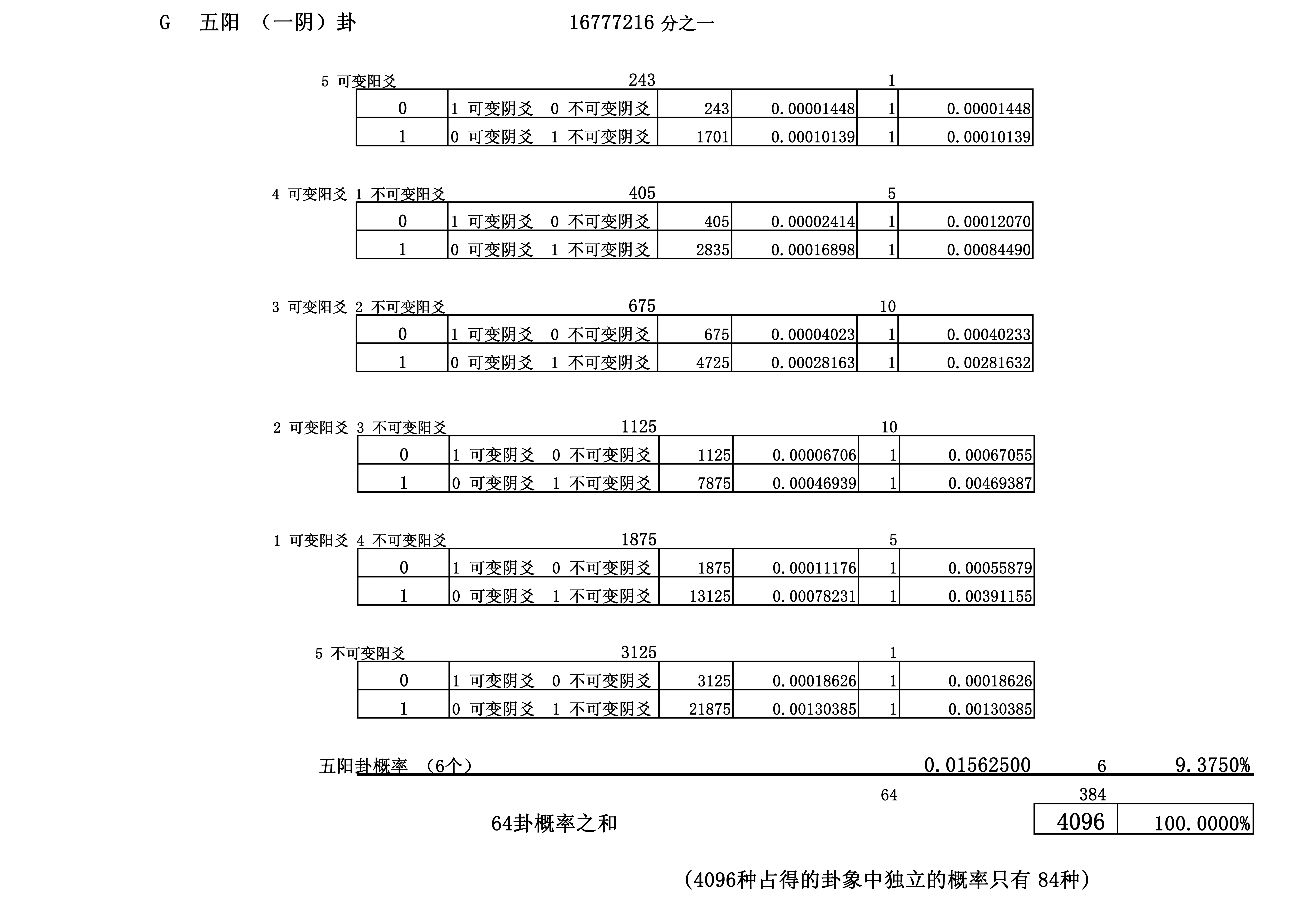
[責任編輯揚眉]