多軸電驅動車輛橫擺穩定性控制仿真研究

楊松樸，曾廣貴，駱志偉，吳春燕

?

多軸電驅動車輛橫擺穩定性控制仿真研究

楊松樸，曾廣貴，駱志偉，吳春燕

（北京航天發射技術研究所，北京，100076）

隨著近年來對行車安全要求的提高，車輛的安全性研究也成為當前車輛研究中重要的一部分，對用于運載、發射等重型車輛尤其如此。對車輛橫擺穩定性的控制是一種主動安全控制的手段，能夠有效地保障汽車行駛過程中的側向穩定性。因此對橫擺穩定性控制方法的研究顯得尤為重要。針對各輪獨立電驅動多軸重型發射車輛的結構特點，建立了二自由度數學模型，利用其各電動輪獨立可控的優點，對基于直接橫擺力矩控制（Direct Yaw-moment Control，DYC）理論的橫擺穩定性控制策略進行了研究和分析。并利用聯合仿真，從響應速度、精確性等方面，驗證了橫擺穩定性控制系統的可行性。仿真結果表明該車輛穩定性控制系統可以使車輛橫擺角速度和質心側偏角得到有效控制，從而提高其穩定性。

穩定性控制；直接橫擺力矩控制；聯合仿真

0 引 言

當車輛在高速下進行轉向操作或受外界其他影響時，側向附著力易達到極限，從而發生危險的橫擺穩定性失穩現象[1]。國外對汽車橫擺穩定性控制的研究較早，2002年投入市場的Bosch公司的第8代ESP在車身橫擺穩定的控制上性能已經十分優越，廣泛應用于中高低檔汽車。目前除了ESP，很多整車廠商都開發了車輛橫擺穩定性控制系統，如Volvo的DTSC、GM的ESC等[2]。而在中國，車輛橫擺穩定性控制的相關研究與國外相比起步很晚，雖然中國現時的ESP等橫擺穩定系統產品的裝配率已經比較高，但實際應用的技術仍沒有掌握[3]。在軍用重型多軸電驅動車的應用方面的相關技術研究更是空白。但隨著中國多軸電驅動車輛的大力發展和對車輛安全性和動力學特性的要求不斷提高，橫擺穩定性相關研究前景良好[4]。

車輛穩定性控制的實現一般通過直接橫擺力矩來防止轉向不足和過度轉向。相比于機械式傳動，各輪獨立電驅動車輛各個車輪驅動力能夠實時地進行獨立控制，車輛的橫擺穩定性控制變得更加靈活有效，電機快速準確的力矩響應使其控制效果比傳統的發動機控制大大提高。本文針對各輪獨立電驅動重型車輛的特點，采用車輛橫擺穩定性典型實施控制方案的直接橫擺力矩控制，通過控制各輪縱向力以形成糾正車輛姿態的橫擺力矩來實現穩定性控制。本文首先對車輛模型進行簡化，建立多軸車二自由度數學模型，并以質心側偏角和橫擺角速度為控制變量，設計基于線性二次型最優控制算法的橫擺力矩控制器，其中前饋控制器的比例增益系數由質心側偏角和橫擺角速度按照變動的權重系數確定，權重系數的取值與多軸車輛的特性相關[5]。然后建立車輛動力學仿真模型和控制模型，通過建立聯合仿真接口，對車輛控制系統進行聯合仿真。

1 橫擺穩定性控制原理

對車輛穩定性的控制屬于主動安全的范圍，控制系統在車輛行駛過程中對行駛狀態進行實時分析，糾正不理想的轉向，并在極限工況下對車輛進行輔助操縱，保證其橫向穩定性。由車輛動力學可知，橫擺角速度和質心側偏角是2個表征車輛行駛狀態的重要量，它們反映了車輛的穩定性[6]。當車輛發生側滑、甩尾等側向失穩的危險現象時，車輛的橫擺角速度與質心側偏角也會偏離理想值，因此將橫擺角速度和質心側偏角進行控制使其處在理想值范圍內是穩定性控制的核心內容。通過對車輪縱向力的控制提供橫擺力矩糾正車輛的轉向不足或過度轉向，減小車輛質心側偏角、使橫擺角速度跟隨理想的穩態橫擺角速度，保持良好的駕駛感覺。

2 數學模型建立

為了進行控制策略的研究，首先對研究對象（即八軸電驅動車輛），進行數學建模，如圖1所示。圖1中將該結構簡化為二自由度模型，其中前三軸與后兩軸為轉向軸，轉向方式為逆相位轉向。

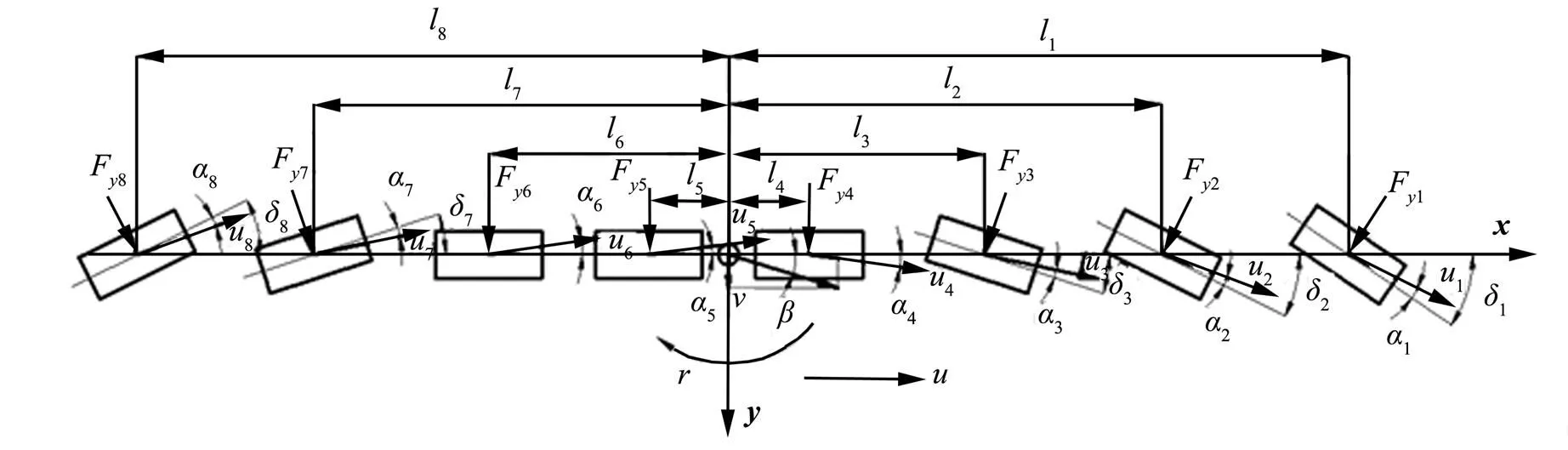
圖1 八軸車的二自由度模型

u—各輪縱向速度；l—第軸到質心的距離；δ—各軸轉角；α—各輪輪胎側偏角；F—各輪輪胎橫向力（以上=1~8）；—縱向速度；—側向速度；—橫擺角速度；—質心側偏角

根據牛頓定律，建立八軸車的線性二自由度車輛模型的運動微分方程[4]：

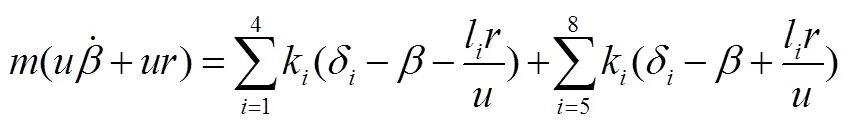
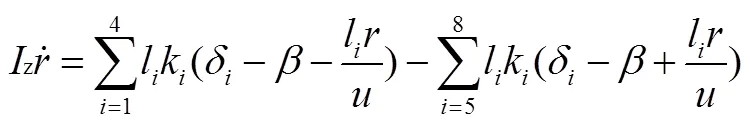
式中為整車質量；k為等效輪胎側偏剛度，總定義為正值；z為汽車的轉動慣量。

根據Ackermann轉角關系，有：

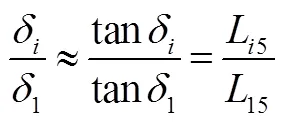
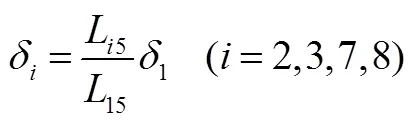
為了能夠更準確驗證控制算法的有效性，八軸車的整車動力學模型采用ADAMS軟件建立。在ADAMS環境中建立38個自由度的整車動力學模型，整車模型包括簧上質量的6個自由度，16個懸架的自由度，16個車輪的自由度，采用UA輪胎模型。

該八軸電驅動車輛配備16個輪邊電機，通過輪邊減速器降速增扭進而驅動各車輪。

3 控制策略與控制器的設計

根據直接橫擺力矩的控制思想，該多軸車輛為各輪獨立電驅動結構，可根據各輪獨立可控的優點實時調整各輪驅動力矩，以保證車輛安全穩定行駛。圖2為控制系統結構，駕駛員模型根據車輛的行駛狀態調整方向盤轉角和油門踏板開度，油門踏板開度決定了整車輸出功率，由此確定各輪輸出的初始驅動力矩T0，當整車的質心側偏角和橫擺角速度與理想值偏差過大時，上層控制器計算出糾正偏差需要的橫擺力矩，由下層控制器按照相應的驅動力分配算法分配至各輪，得到各輪驅動力矩的調整值ΔT，T0與ΔT之和即為各輪實際輸出驅動力矩，方向盤轉角與各輪驅動力矩輸出至整車模型，整車實時運行狀態通過傳感器獲得，經過處理計算反饋至各層。

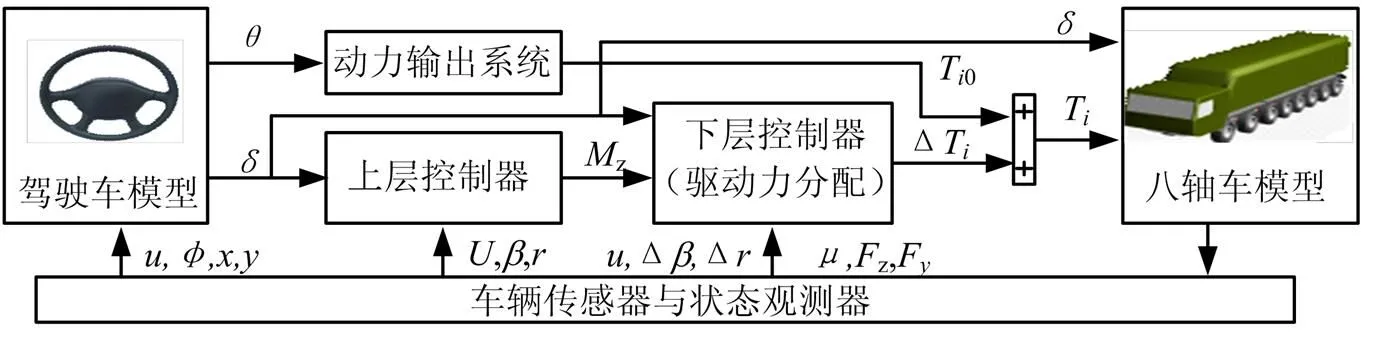
圖2 穩定性控制系統結構示意

3.1 上層控制器設計

上層控制器以駕駛員給定的方向盤轉角、車速、車輛的質心側偏角和橫擺角速度作為輸入，經控制算法得到橫擺力矩，輸出至下層控制器。

圖3為上層控制器結構原理，由整車理想模型、前饋控制器和反饋控制器組成。整車的理想模型由方向盤轉角和當前車速確定，根據車輛達到理想狀態所需的橫擺力矩確定前饋控制器，反饋控制器基于線性二次型最優控制算法對車輛的質心側偏角和橫擺角速度誤差進行糾正。

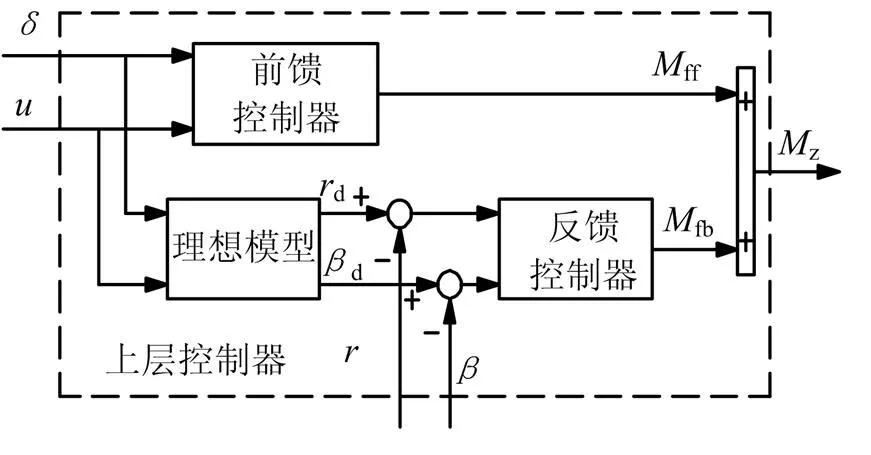
圖3 上層控制器結構原理

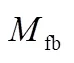
a）控制系統模型。

若給車輛一個附加的橫擺力矩z來控制車輛的操縱穩定性：

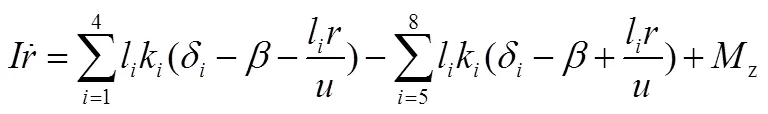
將式（1）、式（2）簡化，得：

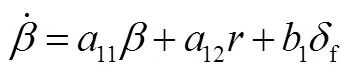
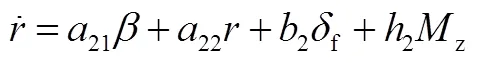
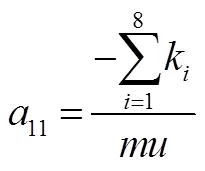
將式（5）、式（6）寫為狀態方程的形式，有：

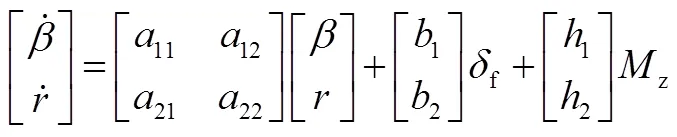
即：

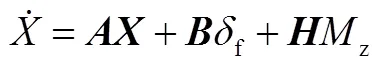
將式（5）、式（6）進行拉普拉斯變換，得：

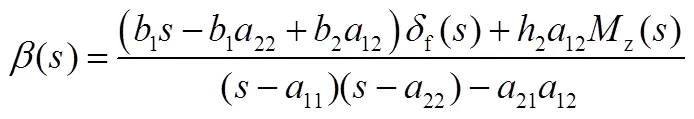
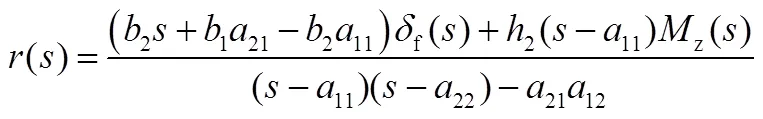
b）前饋補償控制器設計。

前饋控制器是在車輛失穩之前對車輛運動姿態的一種提前預測，目的是使車輛的穩態質心側偏角和橫擺角速度趨于理想值。設計前饋補償控制器，車輛的補償橫擺力矩ff與前輪轉角的關系為

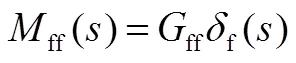
式中ff為前饋控制器的比例增益系數。

首先按照質心側偏角確定的前饋控制系數：將 式（10）代入式（8），可得到穩態轉向時，質心側偏角對前輪轉角的響應為

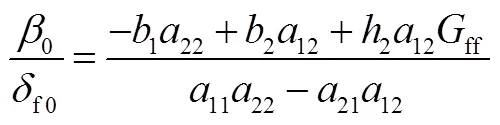
式中f0，0分別為穩態時的前輪轉角及質心側偏角。

理想的質心側偏角大小可簡化為

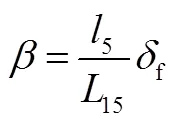
前饋橫擺力矩控制的效果，應該使車輛的穩態質心側偏角達到理想質心側偏角，為此，使β=β，ff0，將式（12）代入式（11）可得：

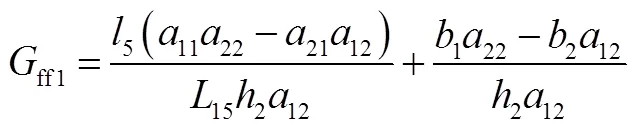
再按照橫擺角速度確定的前饋控制系數：將式（10）代入式（9），可得到穩態轉向時，橫擺角速度對前輪轉角的響應為

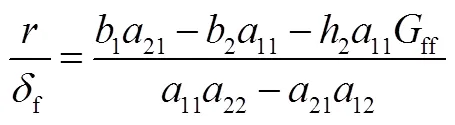
理想的橫擺角速度大小可簡化為

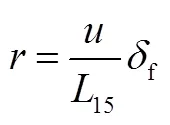
將式（15）代入式（14）可得：

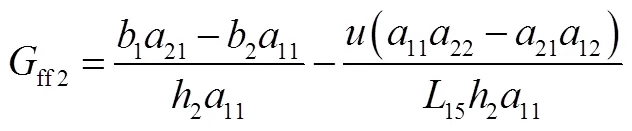
如果只按照質心側偏角進行前饋控制，最終會使得前饋橫擺力矩過大，使車輛的不足轉向趨勢過于嚴重，造成車輛嚴重偏離行駛軌跡；若只按照橫擺角速度進行前饋控制，橫擺力矩不足，使得質心側偏過大。由于車輛的質心側偏角和橫擺角速度是相互耦合的，控制目標必須是兩個能夠同時達到的狀態。因此設計不同權值變量的前饋控制器比例增益系數：

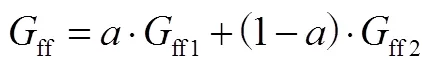
式中為ff1的權重系數，考慮多軸車輛的穩態質心側偏角增益曲線接近于二次函數，因此定義為關于車速的二次函數進行擬合，=2。

c）DYC控制的車輛理想模型。

將式（10）代入式（9），可以得到橫擺角速度的理想傳遞函數：

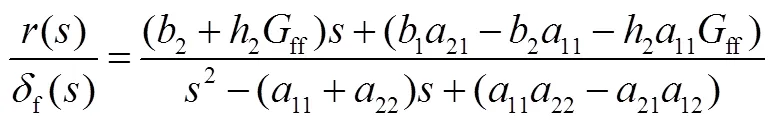
將式（10）帶入式（8），可得到理想的質心側偏角的傳遞函數：

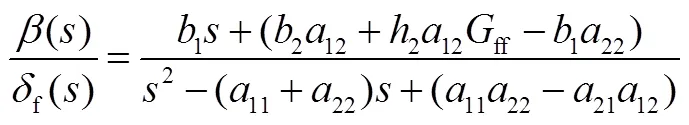
可得理想模型的狀態方程為

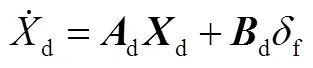
d）反饋控制器的設計。

應用線性二次型最優控制算法設計反饋控制補償器，反饋控制器中實際質心側偏角和橫擺加速度與理想值的偏差為

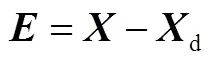
則，

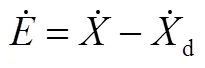
將式（7）和式（20）帶入式（21），可得：

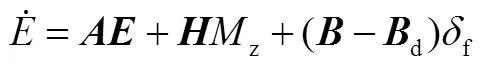
式（22）第3項為前輪轉角引起的干擾項，令其為零，則偏差方程可進一步簡化為

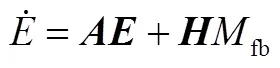
應用線性二次型最優控制算法求解反饋補償增益。設反饋控制系統中的反饋控制力矩為

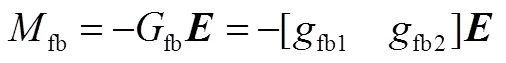
式中fb1和fb2為實際車輛模型與理想模型的狀態偏差反饋增益。

設最小化性能指標函數為

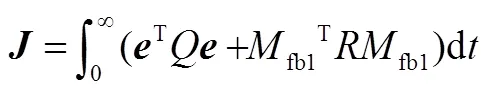
通過線性二次型最優控制算法，求解Riccati方程可得到反饋控制器反饋增益。

因此，總的附加橫擺力矩為

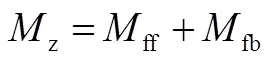
3.2 下層控制器設計

通過上層控制器計算得到糾正車輛姿態所需的橫擺力矩后，建立相應的驅動力分配算法將驅動力分配至各驅動輪。各輪驅動力的調整量ΔFa是根據橫擺力矩確定的，對不同側車輪的驅動力做相反方向的調整。

橫擺力矩分配的原則為：在沒有車輪打滑時對各輪驅動力的調整量按照平均分配原則，從而保證對各輪驅動力最小的調整量；若在平均分配原則下出現打滑車輪，則對各輪驅動力的調整量改為按照各輪垂向力的比值分配，以防再次出現打滑車輪；若按照比值分配后仍然出現車輪打滑，則打滑車輪按照當前最大附著極限分配驅動力，未打滑車輪驅動力調整量仍然按照各輪垂向力的比值分配，但必須保證總的橫擺力矩；最大分配驅動力超過電機所能輸出極限時，該輪驅動力按照電機所能提供值分配，驅動力不足部分由其他未打滑車輪提供。

a）各輪驅動力調整方向的判定。

車輛在小轉向角度發生失穩時，橫擺力矩的控制中僅對左右兩側車輪進行區分即可。但在較大轉角情況下，前輪或后輪的內側車輪形成的橫擺力矩方向改變，以整車右轉為例。圖4為該車處于最大轉角時的示意，其中ΔLia和ΔRia為左右側車輪的驅動力調整量。可以看到，在最大轉角時1、2、8軸內側車輪繞質心的橫擺力矩力臂在質心左側，形成的橫擺力矩方向與外側車輪相同，因此在最大轉角下調整橫擺力矩時，這3個車輪的驅動力調整方向應保持與外側車輪一致，從而保證用最小的驅動力調整量形成最大的橫擺力矩。

當內側前輪轉角從0逐漸增加到最大時，1，2，8軸內側車輪延長線依次越過質心偏向另一側，其驅動力調節方向發生改變。

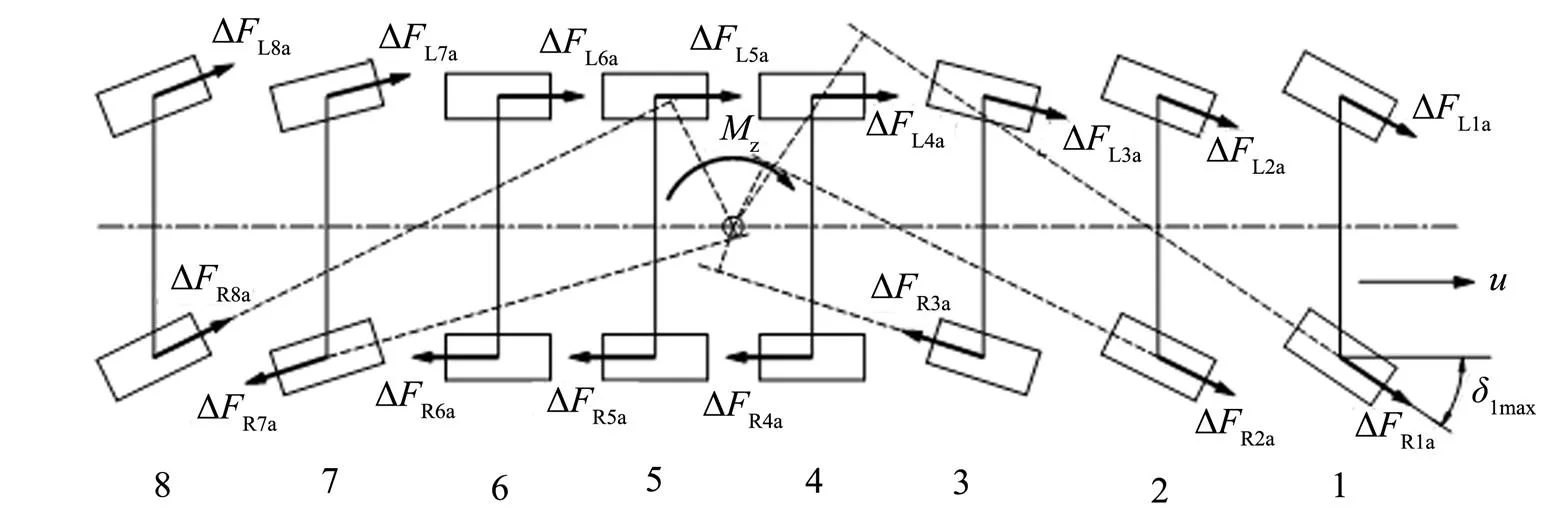
圖4 最大轉角時內側車輪繞質心力臂示意

b）通過橫擺力矩分配各輪驅動力。

定義橫擺力矩z沿順時針旋轉方向時為正，前輪右轉為正，通過各輪驅動力調整量形成的橫擺力矩為

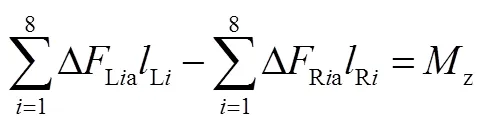
式中 ΔLia和ΔRia為左右側車輪的驅動力調整量，驅動力增加為正，驅動力降低為負；Li和Ri為左右側車輪驅動力在整車質心處形成的力臂，當第軸車輪的力臂與同側車輪力臂不相同時為負，相同時為正。

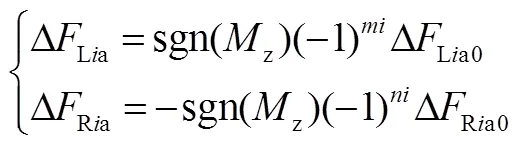
式中和分別為左右兩側車輪的力臂系數，當第軸車輪的力臂與同側車輪力臂不相同時取1，相同時取2，式中ΔLia0和ΔRia0均為正值。

當內側前輪轉角1不為0時，軸內、外兩側輪轉角為

式中分別取1，2，3，7，8；15，25，35為正；75，85為負。

軸內、外兩側輪力臂分別為

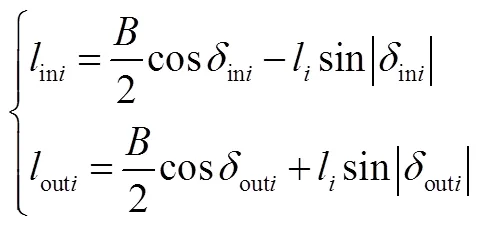
式中為輪距。

因此，左右兩側車輪的力臂為

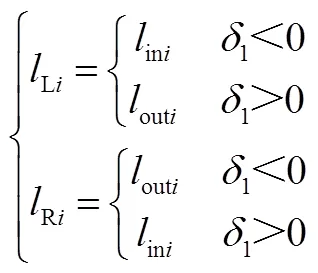
得到由橫擺力矩確定的各輪驅動力的調整量ΔLia0和ΔRia0。

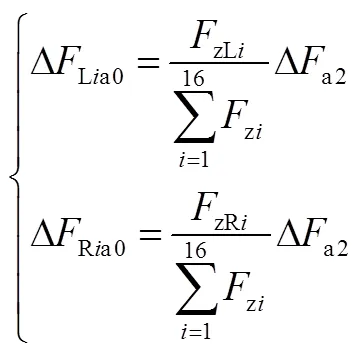
在沒有車輪打滑時對各輪驅動力的調整量按照平均分配原則：

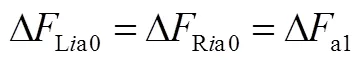
出現打滑車輪時，各輪驅動力調整量按照各輪垂向力的比值分配：

實驗樣車的整車驅動控制系統模型在Matlab/Simulink建模環境下建立，系統模型包括駕駛模塊、初始力矩分配模塊、差速控制模塊、側向穩定性控制模塊、滑轉控制模塊等，如圖5所示。

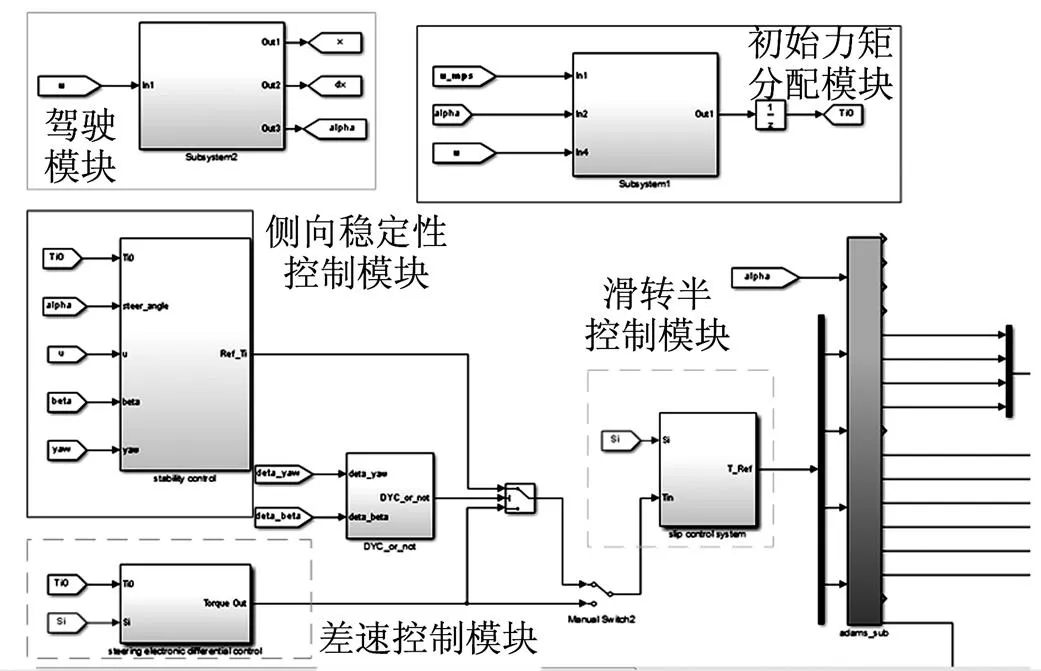
圖5 Matlab/Simulink下整車驅動控制系統

4 仿真驗證

為了驗證所建立的穩定性控制系統的可行性，利用搭建好的整車機械模型和控制模型進行聯合仿真驗證。首先在附著系數=1.0、車速給定值35 km/h時，前輪轉向角輸入4°的轉角階躍函數，對施加控制和不施加控制力矩直接給定直接為初次分配值，分別進行聯合仿真。橫擺角速度和質心側偏角的仿真結果如圖6~8所示。由圖6、圖7可以看出，無控制作用時，橫擺角速度和質心側偏角實際值偏離理想值，存在波動；在控制作用下，車輛的橫擺角速度與質心側偏角均被控制在安全范圍內，橫擺角速度在偏離理想值 1.7 s后，被控制在安全范圍內，超調20%左右，控制效果比較理想。而車速也略有下降后迅速保持原有速度。

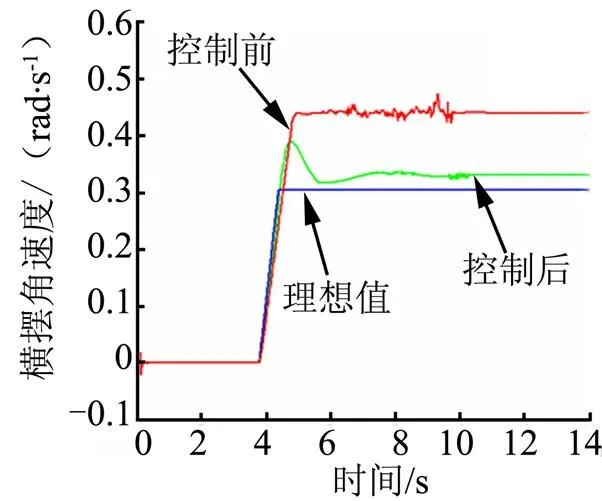
圖6 橫擺角速度響應

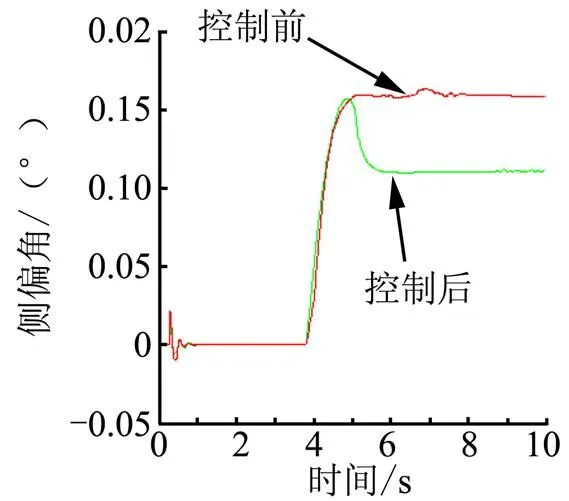
圖7 質心側偏角響應

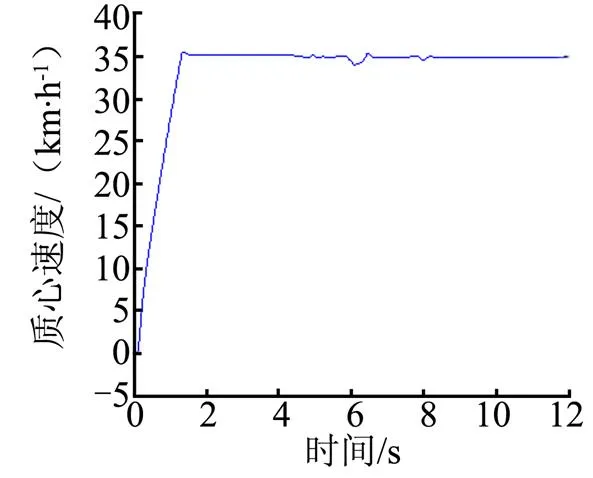
圖8 質心車速仿真曲線

在附著系數=0.3、車速給定值35 km/h時，前輪轉向角輸入4°的轉角階躍函數，對施加控制和不施加控制分別進行聯合仿真。橫擺角速度和質心側偏角的仿真結果如圖9、圖10所示。由圖9、圖10可以看出，無控制作用時，橫擺角速度和質心側偏角嚴重偏離理想值，車輛發生過度轉向偏離理想軌跡，駕駛員已經無法較好地操縱車輛了；而在控制作用下，車輛的橫擺角速度與質心側偏角則被控制在安全范圍內，控制效果比較理想。質心車速仿真曲線如圖11所示，由于路面較滑，轉向時進行控制引起的力矩變化使車速略有波動，但控制結束后恢復穩定。

由此可見，基于線性二次型最優控制理論的橫擺穩定性控制系統性能較好，在保證穩態側偏角為零的同時較好地跟蹤了原有的橫擺角速度。瞬態響應也有較好地改善，側偏角峰值減小，橫擺角速度響應迅速，較好地跟蹤了駕駛員的轉向意圖。

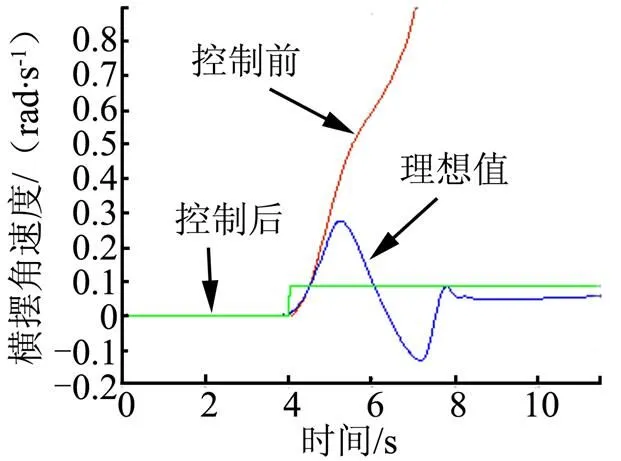
圖9 橫擺角速度響應

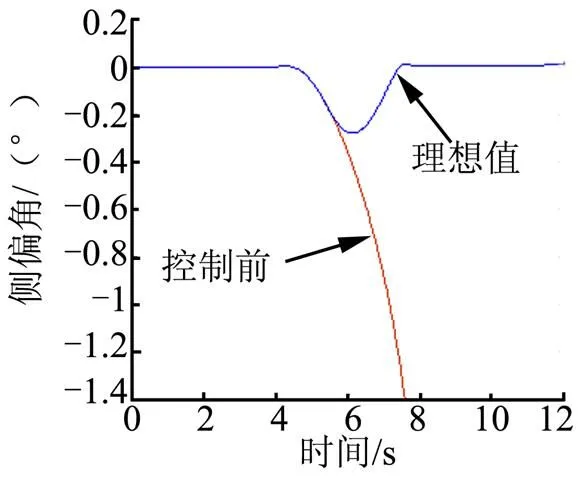
圖10 質心側偏角響應

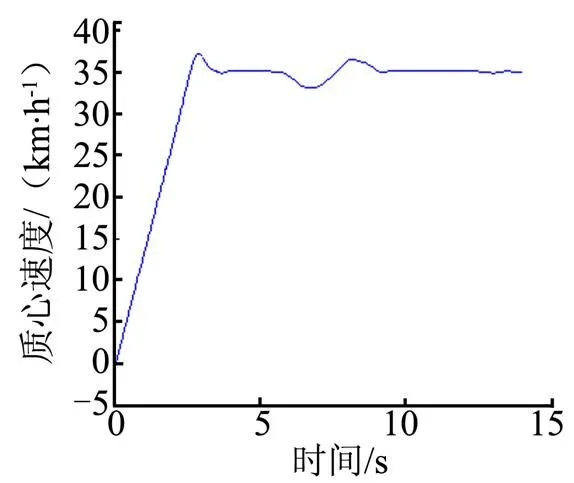
圖11 質心車速仿真曲線

5 結束語

本文針對多軸電驅動重型車輛的結構特點，建立了電驅車輛的二自由度數學模型。應用前饋-后饋控制器，基于線性二次型最優控制算法，設計了基于質心側偏角和橫擺角速度的最優橫擺力矩控制系統，以改善車輛的操縱穩定性。通過仿真分析，所設計的控制方式對整車的操縱穩定性具有良好的控制效果。

[1] Zanten A T V, Rainer E, Georg P.Control aspects of the Bosch-VDC[C]. RWTH Aachen: AVEC, 1996.

[2] 王德平, 郭孔輝, 宗長富. 車輛動力學穩定性控制的理論研究[J]. 汽車工程, 2000(1): 121-202.

[3] Azadzad N L, Khajepour A, Mcphee J. Analysis of jack-knifing in articulated steer vehicles[C]. USA: IEEE Conference on Vehicle Power and Propulsion, 2005.

[4] 汪建春. 鉸接式車輛對擾動的瞬態和穩態響應（上）[J]. 礦山機械, 2008, 36(9): 26-29.

[5] 申焱華. 電驅動鉸接式工程車輛操縱穩定性控制分析[J]. 農業工程學報, 2013, 29(12): 71-74.

[6] 何鋒, 楊寧. 汽車動力學[M]. 貴州: 貴州科技出版社, 2003.

Study on Simulation of Yaw Stability Control ofMulti-axle Electric Driven Vehicle

Yang Song-pu, Zeng Guang-gui, Luo Zhi-wei, Wu Chun-yan

(Beijing Institute of space launch technology, Beijing, 100076)

With the increase of public’s safety awareness, the study of safety of vehicles has become an important part in vehicle research. Controlling of the vehicle yaw stability is an approach of active safety control which can effectively guarantee the lateral stability, hence the significance of the study of the control methods of yaw stability. Aiming on the features of multi-axle electric driven vehicle, this paper researches the strategy of control of yaw stability based on DYC (Direct Yaw-moment Control) theory by establishing vehicle dynamics model.Then the joint simulation was implemented under the typical test．The results illustrates that the control system designed can effectively improve the vehicle yaw stability．

Yaw stability control; Direct yaw-moment control; Joint simulation

1004-7182(2017)06-0082-07

10.7654/j.issn.1004-7182.20170618

U461

A

2016-07-25；

2017-10-31

楊松樸（1990-），男，助理工程師，主要研究方向為電力電子與電力傳動