螺桿數學模型及數控加工銑刀廓形求解

王家祥，楊向紅，孫建軍

（天津工業大學機械工程學院，天津300387）

引言

梯形螺桿將旋轉運動轉換成直線運動、將扭矩轉換成推力等優點而被大量使用在航空航天、海洋領域以及生產的各行各業。由于其截面型線的多樣性和加工過程中空間嚙合的復雜性，導致螺桿嚙合間隙不均勻、運轉振動大、齒間嚙合出現局部干涉，使得梯形螺桿普遍存在嚙合沖擊大、壽命低等問題。賈寅等人基于螺桿真空泵針對單頭梯形螺桿齒頂圓周螺旋升角小于齒根圓周螺旋升角,在兩螺桿齒間嚙合區，一螺桿的齒頂部分與另一螺桿的齒根部分上升速率不一，導致產生根切現象,即運動過程中出現二級轉子齒間干涉[1]進行型線研究[2]。張世偉等針對單頭等螺距梯形螺桿轉子型線的干涉問題提出平移齒面法和內凹齒面法[3]，并未涉及各型線方程之間的一階連續性問題。基于螺桿加工過程中的嚙合情況，趙春秀等對成型銑刀加工螺桿過程的坐標計算進行了研究[4]，景寧等建立了圓柱立銑刀成型加工螺桿曲面模型[5]，Yang等使用逆包絡法的思想建立了11∶6單螺桿壓縮機的數字化模型并進行了加工刀具的設計[6]，王艷琴等建立并仿真了球頭銑刀加工螺桿的過程[7]。刀具刃形的求解方法無法解決任意型線的情況，尤其展現于對螺桿齒形曲線的光滑連續性方面。本文采用內凹齒面法設計螺桿截面型線，解決了螺桿截面各型線之間的一階連續問題，有效避免齒間干涉的出現，建立并解析出螺桿曲面模型。基于空間包絡原理，對解析出的螺桿模型，將螺桿齒形離散成一系列離散點，研究螺桿于刀具加工過程中的空間嚙合特性和幾何特性，建立工件—刀具坐標轉換方程，結合嚙合原理解析出刀具接觸跡方程、刀具軸向刃形。

1 螺桿三維建模

1.1 等螺距螺旋面方程

在圖1中，該螺旋面是由曲線c沿著z軸方向作等速移動，同時沿著z軸作等速旋轉形成，即由曲線c沿著軸向作螺旋運動形成。建立如圖1所示的直角坐標系（x，y，z），三個坐標的矢量分別表示，引入端截面角度參數φ，可以得到已知的螺桿端截面曲線c的坐標方程為：

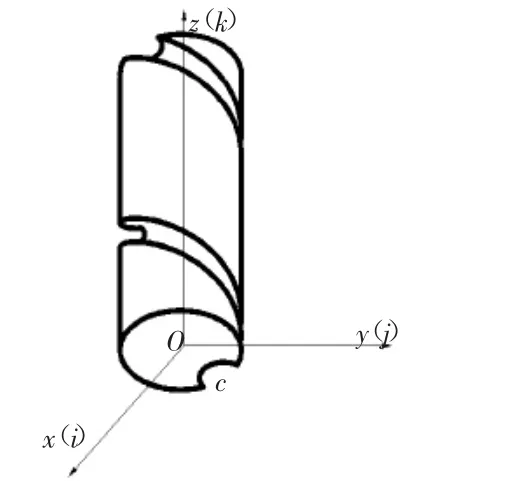
圖1 螺旋曲面

若已知的螺桿端面廓形——曲線c繞著z軸轉過一個角度θ，同時曲線c沿著z軸方向以導程pz上升一個距離時，引入螺旋參數p來表示，其中p=pzθ/（2π）[8-9]，則上式沿螺旋線形成的左螺旋面方程可以表達成：

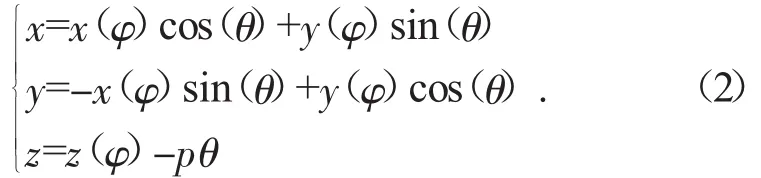
右螺旋面方程則為：

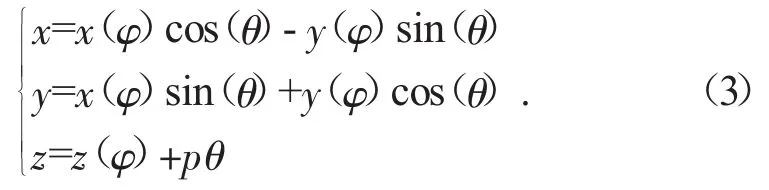
式中：θ為角度參數，表示母線沿z軸轉過的角度，沿著z軸看，以順時針為正；p為螺旋參數，表示母線繞z軸轉過單位角度，沿z軸方向移動的距離[10]。

由式（2）或式（3）可知，若以θ為常數，而只改變φ，可得到不同軸向位置處的端截面廓形曲線。反之，保持φ為常數，而改變θ，便可得到該螺旋面上的一系列螺旋線[11-12]。

1.2 單頭等螺距內凹螺桿形線設計

螺桿的截面線型一般有對稱圓弧型線、不對稱圓弧型線以及新型不對稱型線等，常用的是漸開線和擺線[13]。本文用漸開線、擺線和圓弧曲線作為所要設計的單頭等距內凹螺桿的形線，如圖2和圖3所示。對于螺桿的左、右旋向而言，在實際制造過程中其線形設計基本參數一致，左右旋向不同，從而配對成一對螺桿轉子。

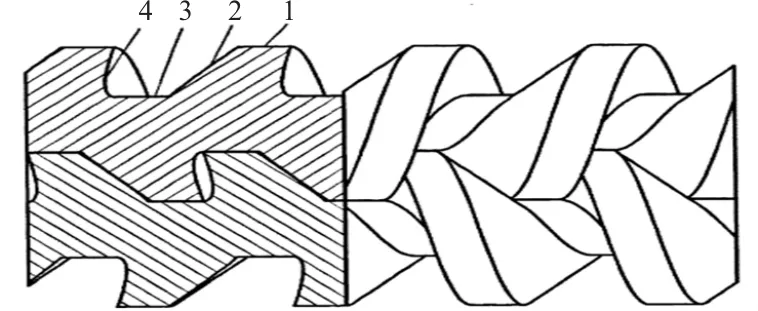
圖2 螺桿嚙合半剖示意圖

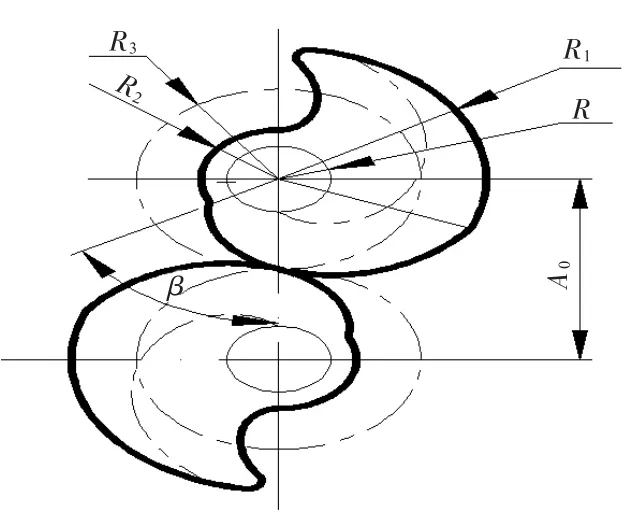
圖3 螺桿截面嚙合示意圖

如圖2所示，1為齒頂圓線形，2為漸開線線形，3為齒根圓線形，4為內凹擺線線形。螺桿嚙合點處的端截面形線則如圖3所示，主要參數包括：嚙合中心距A0，齒頂圓半徑R1，齒根圓半徑R2，漸開線的生成圓半徑R，理論嚙合圓其半徑R3，以及參數p（p=導程（/2π））。其中：

所設計的螺桿端截面各段截面形線方程分別為：

1）齒頂圓方程：

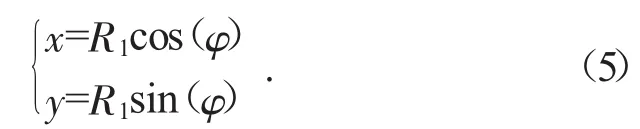
2）齒根圓方程：

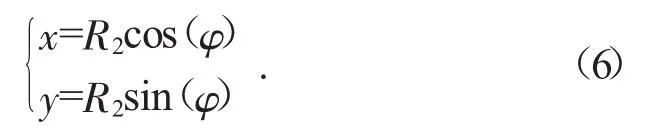
3）漸開線部分是由標準漸開線方程先順時針旋轉π/2，同時為了使得嚙合點位于兩嚙合圓心連線上，需再將漸開線方程順時針旋轉β角。本文中的漸開線方程是由標準漸開線方程經過這兩步旋轉變化所得，其方程的矩陣形式為：

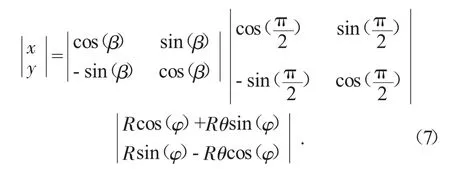
4）擺線部分亦是由擺線的標準方程逆時針旋轉π/2所得，則其方程矩陣表達式為：

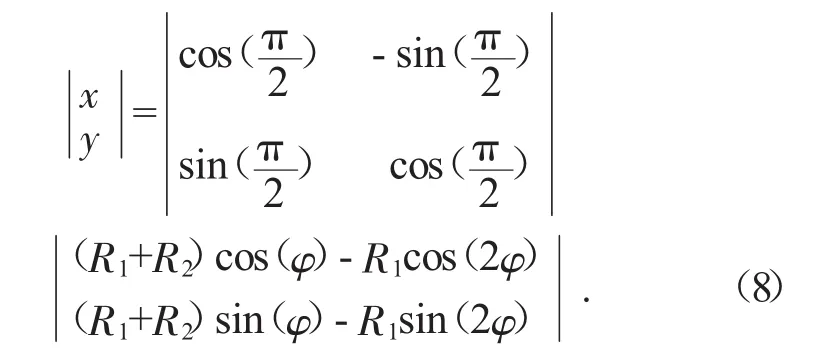
初步設計的截面形線中齒根圓與漸開線、漸開線與齒頂圓、齒頂圓與擺線相交點處一階導數不存在，導致螺桿運動過程中產生較大的震動、兩螺桿間嚙合不順暢，損耗螺桿的使用壽命，因而必須減少不可導點的出現。為了能夠使得各段形線連接點處導數存在，本文采用圓弧過渡的方法：

齒根圓與漸開線部分采用外切圓弧過渡，設此圓弧方程為：

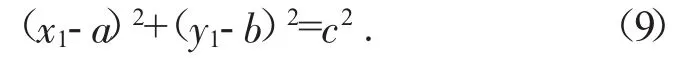
其中：（a，b）為過渡圓弧圓心點坐標，c為過渡圓弧半徑。則聯立公式（6）和（9）可得方程組（10），即可得到過渡圓弧與齒根圓的交點：

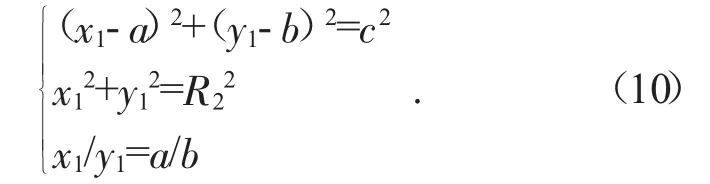
聯立公式（7）和（9）可得方程組（11），即得到過渡圓弧與漸開線的交點：

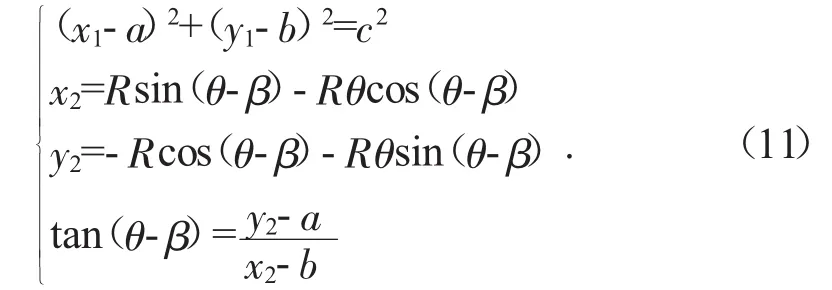
通過給定過渡圓弧半徑，求解方程組（10）（11），可得兩個交點坐標（x1，y1），（x2，y2），由這兩點坐標與過渡圓弧半徑就可確定過渡圓弧圓心位置。此外把點（x1，y1）代入到公式（6），可求解出齒根圓終止角θ1；把（x2，y2）代入到公式（7），可求得漸開線部分的起始角θ2。

齒頂圓與漸開線采取內切圓弧過渡，同上可確定此時過渡圓弧圓心位置，并求解齒頂圓起始角與漸開線終止角。對于齒頂圓與內凹擺線處的過渡方式，可用內切圓弧過渡，求解出過渡圓弧圓心位置，并確定齒頂圓和內凹曲線的終止位置。

根據上文推導，代入各個參數的實際賦值（R=20，R1=80，R2=30，c=5），通過C語言編程計算，將求解出的數據用Grapher繪制，得到如圖4所示含過渡曲線的螺桿數學模型圖：

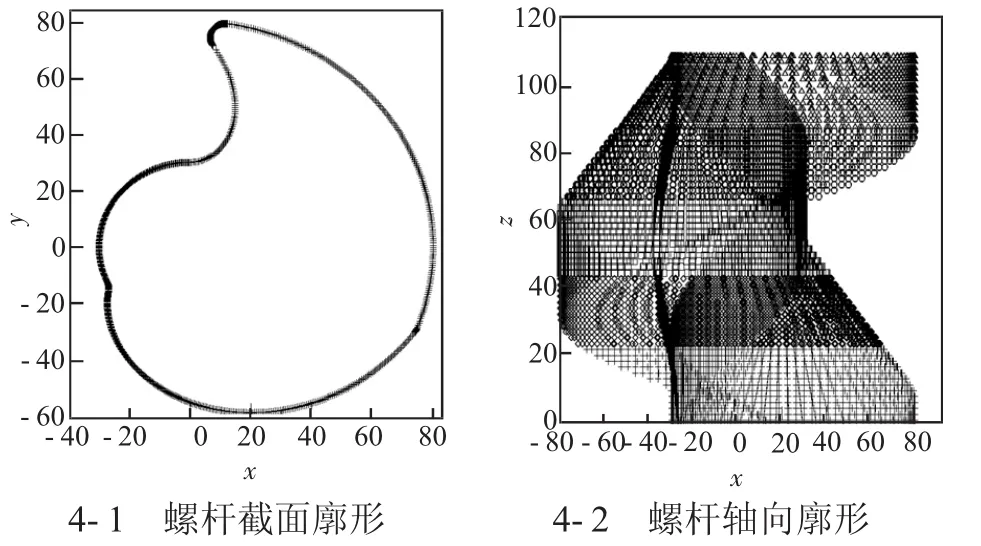
圖4 螺桿數學模型圖

2 刀具及工件坐標系的建立

考慮螺桿的實際加工過程，建立刀具模型，基于包絡法加工螺桿[14]的過程確定工件和刀具坐標系的轉換關系。由于銑刀在加工過程中一直處于旋轉狀態，所以可以將刀具模型簡化為其旋轉過程中形成的回轉工作面，即將刀具的回轉工作面作為所要建立的刀具模型。

如圖5所示，使刀具沿著工件坐標軸x正方向由遠及近進行運動，在工件和刀具達到接觸時，接觸點稱為第一接觸點即為刀具與工件接觸的初始位置（初始切削點位置）。

2.1 銑刀方程的建立

成形銑刀工作的有效切削表面是其形成的回轉面，其結構可以簡化為如圖6所示。

則刀具簡化模型的軸向截形即刀具廓形方程可表示為：

其中：R表示刀具表面點刀刀具軸線的距離，zr表示刀具軸向坐標值，即刀具厚度。

2.2 刀具與工件坐標系的關系

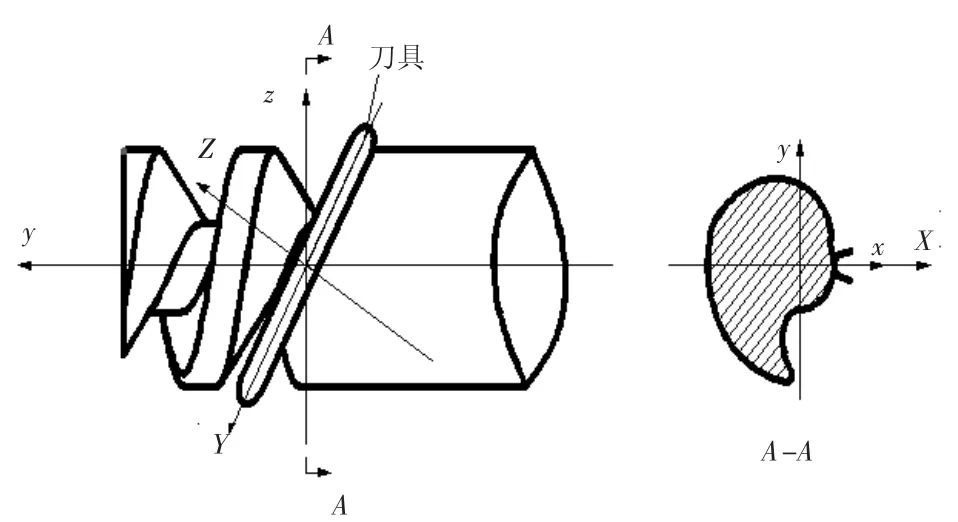
圖5 包絡法加工示意圖

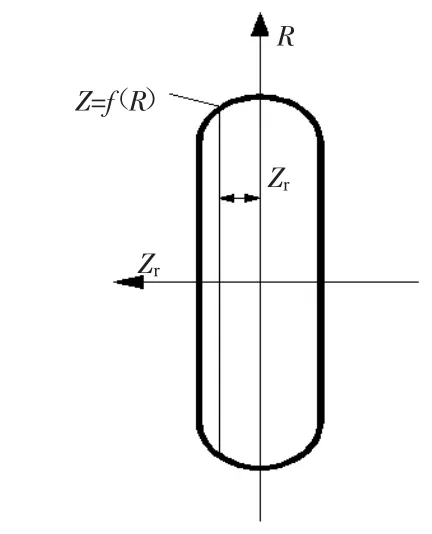
圖6 刀具簡化模型示意圖

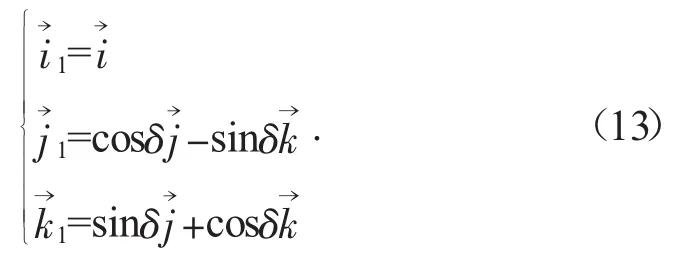
3 刀觸點軌跡的推導與驗證

基于空間包絡法，工件與刀具是點對點的接觸切削，且工件表面曲線與刀具表面曲線是一對共軛曲線，則滿足共軛曲線接觸的三個基本條件[15]：

1）在接觸點處位置重合；

2）在接觸點處相切；

3）在共軛接觸點處，該點處的瞬時運動速度方向必須垂直于該點處的公法面即垂直于兩曲面內任意法線。

螺桿是由工件繞著C軸的旋轉運動與刀具沿著螺桿z軸向的進給運動包絡而成。若設取螺桿面上一點M（x，y，z），則該點相對于兩個坐標系原點的徑矢為：

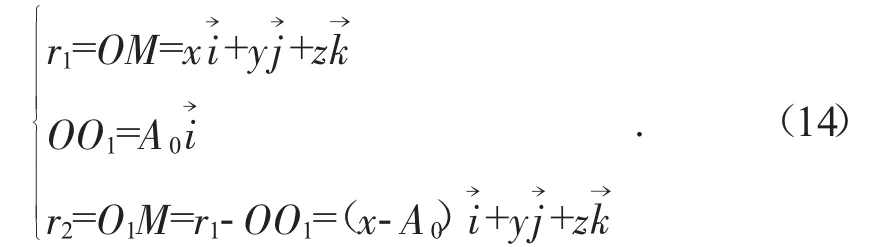
設刀具回轉角速度為ω2，工件螺旋面回轉的角速度為ω1，并以pω1勻速沿螺桿z軸向平移以滿足螺旋面自身的螺旋運動。

則M點處隨螺旋面運動的線速度為：

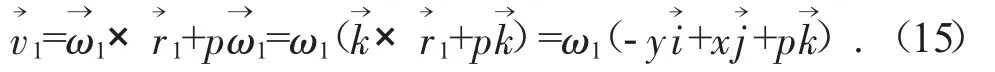
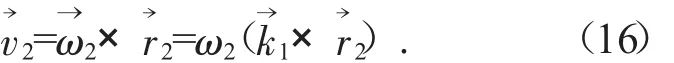
M點處隨刀具運動的線速度為：將式（13）和式（14）代入式（16）整理得：由嚙合原理可得：

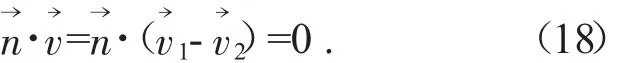
根據右螺旋方程矢量表達式可以求解出右螺旋螺桿曲面上任意一點M（x，y，z）處的法矢量方程→n：

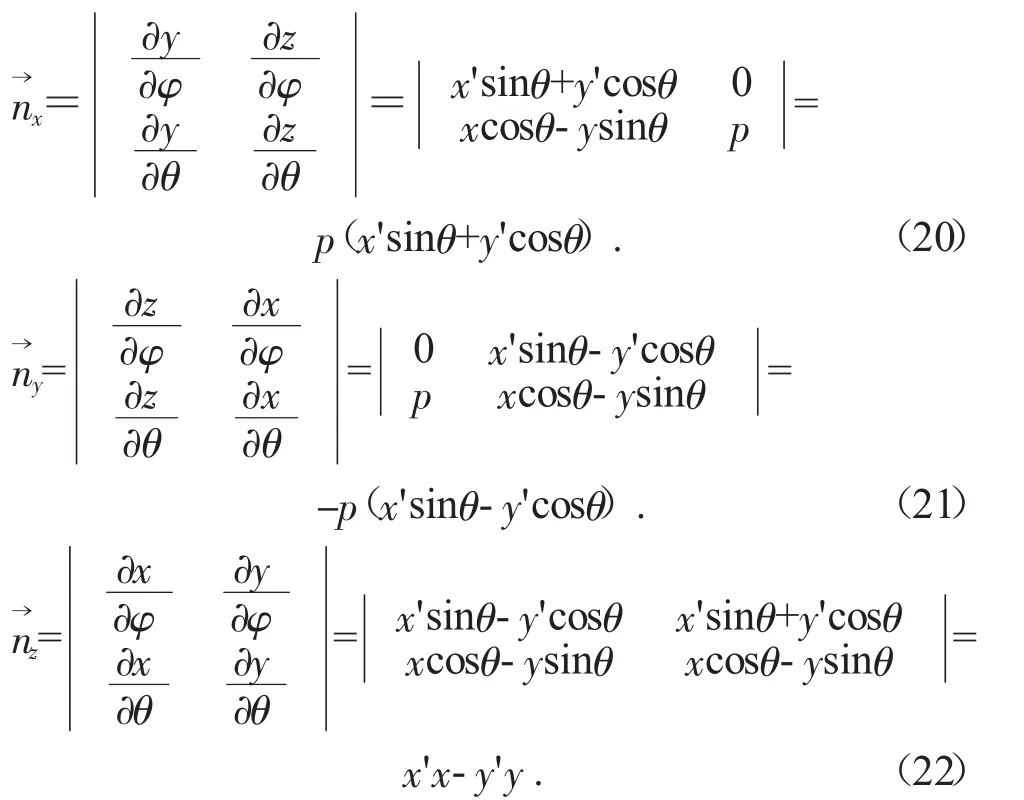
則由矢量運算法則得：整理式（20）、式（21）、式（22）可得：

稱式（23）為右螺旋面特性方程。

同理可以得到左螺旋面特性方程：

將式（15）、式（16）、式（23）代入式（18），化簡整理得：

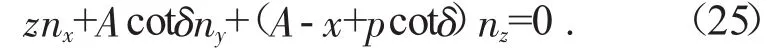
式（25）稱為刀觸點方程，在工件的端面截形上取一個定φ值，則可以通過式（25）可以求解出一個對應的θ值，表示工件截面上的一個坐標點按螺旋運動旋轉過θ后成為接觸點，將點（φ，θ）代入螺旋面方程就得到了一個接觸點，一系列的接觸點構成了空間的接觸線（也稱為接觸跡）。將接觸線繞著刀具回轉軸線進行回轉，可得到刀具的回轉面。利用坐標變換式（13）將接觸點轉換到刀具坐標系O-XYZ中，得到坐標（x1，y1，z1），將一系列離散點通過轉換方程求解出的坐標代入式（11）可得到銑刀軸向截形。

其中，取A0=140 mm，p=110.0/（2π），R=80.0 mm，δ=41.197352°，δ所取的值為被加工螺桿的螺旋升角，用C語言編程求解，可以求解出刀具廓形上的點，如圖7所示。

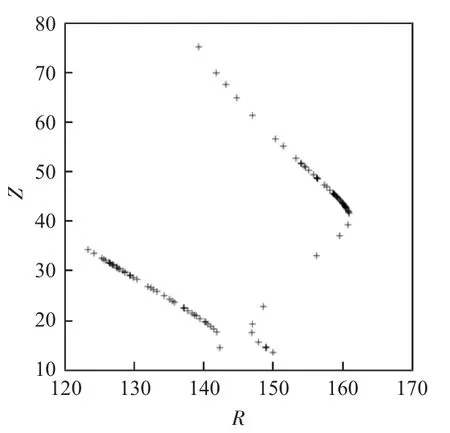
圖7 銑刀廓形截面點分布圖

如圖7所示，求解過程中存在導數無窮大點，所以求解處的廓形曲線上有突變點，對突變點處進行修整，整理數據可得到銑刀在廓形截面上的刀具厚度與半徑之間的函數圖像關系。對上圖中的銑刀截形使其繞著刀具軸線R=0旋轉一周即可得到完整的銑刀廓形。

4 結論

1）為避免齒間嚙合干涉，針對單頭等螺距梯形螺桿進行形線設計，解析各形線方程、起始點位置，求解出一系列的離散點坐標，并用Grapher進行坐標點圖形繪制；

2）提出應用空間包絡法加工螺桿，建立刀具與工件的坐標轉換關系以及簡化的刀具模型；

3）研究空間包絡法加工工件的過程，并根據加工時刀具與工件所必須符合的嚙合原理推導出刀觸點方程，求解出刀位接觸點軌跡的方程，通過C語言依據坐標轉換關系編程解出工件上離散接觸點對應的刀具接觸點坐標，得出了刀具廓形。

[1]Stosic.N.On gearing of helical screw compress rotors[J].Proceedings of the Institution of Mechanical Engineers Part C:Journal ofMechanical EngineeringScience,1998,212(7):587-594.

[2]陳長琦，賈寅，鄭定保，等.螺桿真空泵單頭等螺距內凹轉子型線研究[J].真空，2011（3）：8-11.

[3]張世偉，徐成海，祖文文，等.單頭等螺距梯形齒螺桿轉子型線的干涉問題研究[J].真空科學與技術學報，2007（1）：46-49.

[4]趙春秀，劉建寧.螺桿加工成型銑刀廓形坐標計算方法[J].機械設計，2008（6）：69-70.

[5]景寧，孫麗，王秀倫.用標準圓柱立銑刀加工成形圓柱螺旋曲面機理的研究[J].機床與液壓，2001（4）：30-33.

[6]YANG，CHENGS.Modeling and manufacturing of pp-type single screw compressor[J].Transactions of the Canadian Society for Mechanical Engineering,2007,31(2):219-234.

[7]王艷琴.螺旋轉子的幾何建模與數控加工仿真[D].合肥：合肥工業大學，2006.

[8]張元勛，唐倩，江振偉，等.基于嚙合間隙的螺桿齒形設計與成形加工方法[J].機械工程學報，2014（9）：48-57.

[9]姜淼.一種特殊螺旋曲面及其共軛曲面的研究[D].沈陽：沈陽工業大學，2009.

[10]萬久遠.特種供送螺桿關鍵技術研究[D].秦皇島：燕山大學，2015.

[11]宋玉杰，王力，韓國有.基于UG的單螺桿泵參數化建模[J].油氣田地面工程，2008（3）：23-24.

[12]STOSICN,SMITHIK,KOVACEVICA,et al.Geometry of screw compressor rotors and their tools[J].Journal of Zhejiang University，2011，12（4）：310-326.

[13]張世偉，徐成海，關奎之.螺桿真空泵單頭變螺距螺桿轉子型線的研究[J].真空，2002（4）：9-11.

[14]趙文珍，楊向紅，孫新，等.包絡法數控加工螺桿的刀具軌跡計算方法[J].組合機床與自動化加工技術，2000（5）：20-25.

[15]陳兵奎，梁棟，高艷娥.齒輪傳動共軛曲線原理[J].機械工程學報，2014（1）：130-136.