基于EEMD和CICA的風(fēng)電機(jī)組軸承故障特征提取

許崇新，徐樊浩

（國(guó)網(wǎng)山東省電力公司煙臺(tái)供電公司，山東 煙臺(tái) 264001）

0 引言

作為一種具有大規(guī)模應(yīng)用的清潔能源，風(fēng)能發(fā)電在電網(wǎng)滲透率日益增高。風(fēng)電機(jī)組作為風(fēng)能發(fā)電的核心設(shè)備，保證其安全穩(wěn)定運(yùn)行顯得至關(guān)重要。而風(fēng)電機(jī)組運(yùn)行環(huán)境相對(duì)惡劣，且安裝位置高，不便于檢修。為此，研究人員開(kāi)展了一系列有關(guān)風(fēng)電機(jī)組的狀態(tài)監(jiān)測(cè)研究工作，盡早發(fā)現(xiàn)故障，避免事故擴(kuò)大［1］。風(fēng)電機(jī)組多個(gè)部位裝配有軸承，諸如主軸、齒輪箱等，軸承故障在風(fēng)電機(jī)組故障中所占比例很高［2］。

振動(dòng)信號(hào)分析方法是軸承等機(jī)械設(shè)備狀態(tài)監(jiān)測(cè)與故障診斷的主要方法之一。目前，快速傅里葉變換FFT（Fast Fourier Transform）［3］、小波變換［4］、經(jīng)驗(yàn)?zāi)B(tài)分解［5-6］（Empirical Mode Decomposition，EMD）等方法常被用來(lái)分析軸承等機(jī)械設(shè)備的振動(dòng)信號(hào)。但是這些方法存在一定的缺陷，諸如FFT只適合處理平穩(wěn)信號(hào)、小波變換中小波基的選取對(duì)結(jié)果影響較大、經(jīng)驗(yàn)?zāi)B(tài)分解存在模態(tài)混疊等。為解決模態(tài)混疊問(wèn)題，Huang等人提出的EEMD方法在需要分解的信號(hào)中引入白噪聲，不但可以抑制EMD方法中存在的模態(tài)混疊問(wèn)題，而且可以將需要分解的信號(hào)與白噪聲當(dāng)作一個(gè)整體進(jìn)行EMD分解。因此，利用EEMD方法對(duì)測(cè)得的風(fēng)電機(jī)組軸承故障振動(dòng)信號(hào)進(jìn)行自適應(yīng)分解，并選取能體現(xiàn)軸承故障特征的本征模函數(shù)（Intrinsic Mode Function，IMF），對(duì)于提取軸承故障振動(dòng)信號(hào)特征具有重要價(jià)值［7］。此外，這些方法均是直接分析測(cè)得的變壓器振動(dòng)混合信號(hào)，得到的信號(hào)特征成分比較復(fù)雜，不易于辨識(shí)具體的異常狀況。

基于參考信號(hào)的獨(dú)立分量分析方法（Constrained Independent Component Analysis，CICA） 是在獨(dú)立分量分析（Independent Component Analysis，ICA）的基礎(chǔ)上發(fā)展而來(lái)，近年來(lái)普遍應(yīng)用在生物醫(yī)療、圖像以及語(yǔ)音信號(hào)處理等問(wèn)題上。其應(yīng)用先驗(yàn)知識(shí)建立能夠表征目標(biāo)信號(hào)時(shí)間特性的參考信號(hào)，將其引入基于參考信號(hào)的獨(dú)立分量分析運(yùn)算中，形成某種約束限制算法的收斂方向，從而可以從多異常混合信號(hào)中得到目標(biāo)異常的特征信息。文獻(xiàn)［8］采用CICA方法從人臉圖像和功能磁共振數(shù)據(jù)中提取了有效特征信息；文獻(xiàn)［9］利用感興趣信號(hào)的周期特性，建立脈沖參考信號(hào)，從而采用CICA方法分離出軸承故障信號(hào)。但是在實(shí)際應(yīng)用中，有些時(shí)候軸承的先驗(yàn)知識(shí)不容易確定，并不能建立較好的參考信號(hào)，從而限制了該方法的應(yīng)用。

為解決上述問(wèn)題，提出基于EEMD和CICA的風(fēng)電機(jī)組軸承故障特征提取方法對(duì)風(fēng)電機(jī)組軸承故障振動(dòng)信號(hào)進(jìn)行分析。根據(jù)EEMD方法分解信號(hào)的特點(diǎn)，并結(jié)合信號(hào)獨(dú)立性要求，建立參考信號(hào)。然后利用CICA方法提取軸承故障中包含的信號(hào)特征，并進(jìn)行包絡(luò)解調(diào)得到包絡(luò)譜。分析實(shí)測(cè)實(shí)驗(yàn)數(shù)據(jù)表明，該方法不僅能夠?qū)崿F(xiàn)信號(hào)特征提取，而且可以實(shí)現(xiàn)故障與正常振動(dòng)信號(hào)特征的分離。

1 風(fēng)電機(jī)組軸承故障振動(dòng)信號(hào)EEMD

風(fēng)電機(jī)組軸承故障振動(dòng)信號(hào)EEMD方法具體步驟為：

1）初始化EMD次數(shù)N，選擇加入白噪聲的幅值系數(shù)k。

2）向測(cè)得的軸承故障振動(dòng)信號(hào)x（t）中加入 N次均值為0，幅值系數(shù)為k的高斯白噪聲序列ni（t）（i=1，2，…，N），即

3）對(duì)得到的xi（t）分別進(jìn)行 EMD 分解，得到各個(gè)IMF分量和殘余項(xiàng)，即

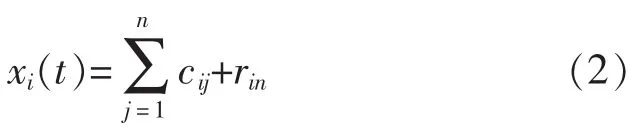
式中：cij為第 i次引入高斯白噪聲信號(hào)后，對(duì) xi（t）進(jìn)行分解得到的第j個(gè)IMF分量；rin為第i次加入高斯白噪聲后，對(duì)xi（t）進(jìn)行分解后的余項(xiàng)；n為分解層數(shù)。

4）將通過(guò)上述步驟得到的IMF分量進(jìn)行總體平均運(yùn)算，抵消引入高斯白噪聲信號(hào)所帶來(lái)的影響，最終得到EEMD方法對(duì)應(yīng)的IMF分量為

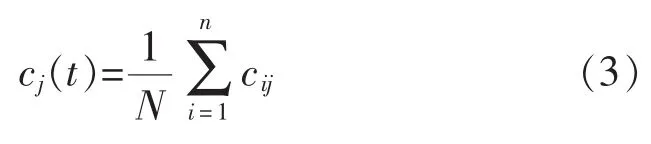
式中：cj（t）為EEMD方法分解軸承故障振動(dòng)信號(hào)后所得到的第j個(gè)IMF分量。

2 風(fēng)電機(jī)組軸承振動(dòng)信號(hào)特征提取

2.1 CICA算法

CICA算法的基本模型為［10］

目標(biāo)函數(shù)：

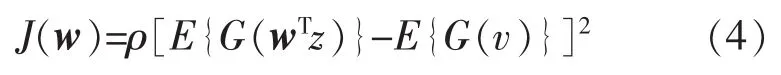
約束條件：

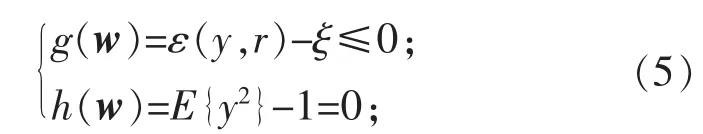
式中：ρ為正常量；w為使目標(biāo)函數(shù)極大的估計(jì)系數(shù)矩陣；E｛·｝為期望值；z為輸入信號(hào)；y=wTz為輸出信號(hào)；r為參考信號(hào)；v為零均值、單位方差的高斯變量；G（·）為任意一個(gè)非二次方程；g（w）為相似性測(cè)度參數(shù)；ξ為閾值參數(shù)；ε（y，r）為源估計(jì) y 和 r之間的廣義距離函數(shù)；h（w）為獨(dú)立分量等式約束。根據(jù)高斯性的不同，G（·）可以取以下函數(shù)：

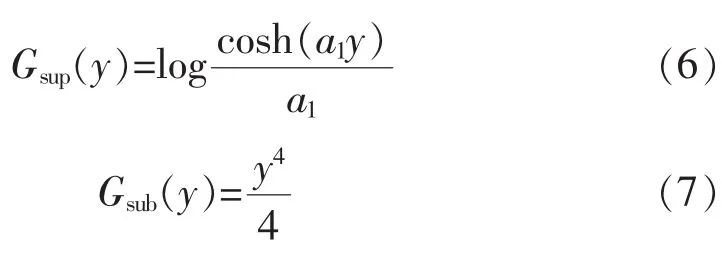
式中：1≤a1≤2，a2≈1。 根據(jù) y和 r的差異程度的不同，可以選擇或者ε（y，r）=-（E｛（yr）｝）。 ξ是門(mén)限，用于區(qū)分目標(biāo)信號(hào)與其他信號(hào)，其取值范圍為

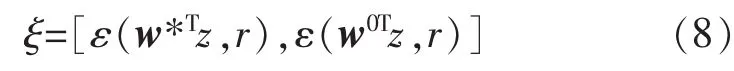
為了獲得在條件式（5）約束下目標(biāo)函數(shù)式（4）的最優(yōu)解，首先建立拉格朗日函數(shù)

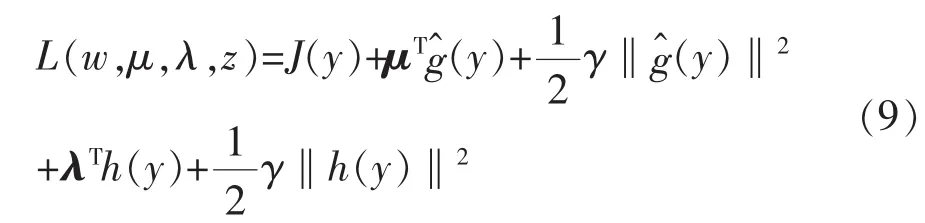
極大化拉格朗日函數(shù)式（9），即可獲得單元CICA的Newton-like算法為

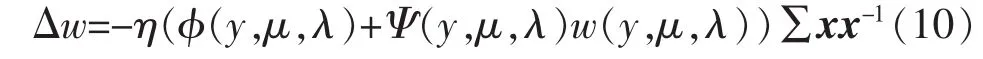
其中，

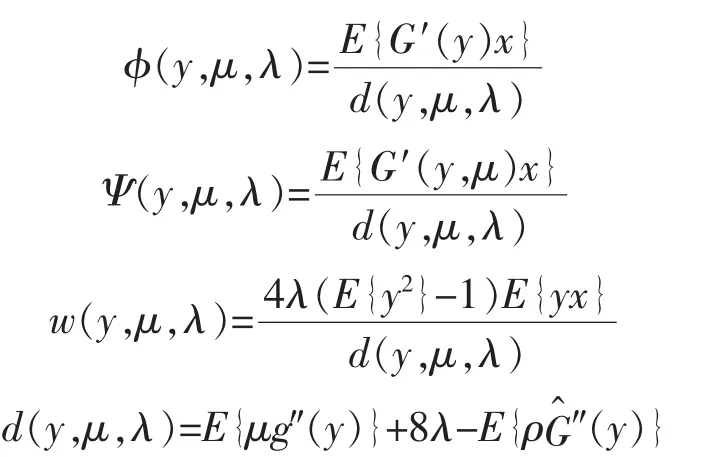
式中：G′y（y）、G″y（y）和 g′（w）、g″（w）分別為 Gy（y）、g（w）的一階導(dǎo)數(shù)和二階導(dǎo)數(shù)；μ、λ為拉格朗日因子，由以下迭代算法得到：

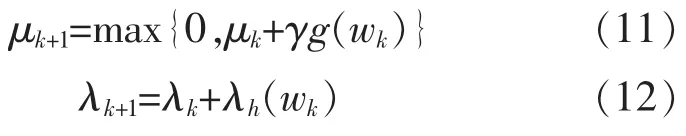
2.2 參考信號(hào)的選取

采用EEMD方法對(duì)軸承故障振動(dòng)信號(hào)x（t）進(jìn)行分解，得到若干 IMF 分量 ci（t）（i=1，2，…，d）及殘余項(xiàng)。將及其IMF分量重新組合，得到一個(gè)虛擬的多通道傳感器觀測(cè)信號(hào)則虛擬信號(hào)xIMF（t）的協(xié)方差矩陣Rx可表示為

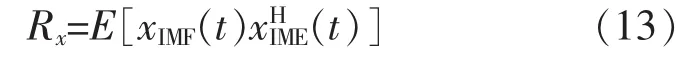
對(duì)協(xié)方差矩陣進(jìn)行奇異值分解，可以有效消除軸承故障振動(dòng)信號(hào)中包含的噪聲成分，得到相對(duì)純凈的特征信號(hào)。協(xié)方差矩陣Rx的奇異值分解為

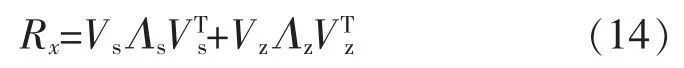
式中：Λs=diag｛λ1，…，λd｝表示為 d 個(gè)按照遞減順序排列的主特征值；ΛZ＝diag｛λd+1，…，λv｝表示為 v-d 個(gè)噪聲特征值。

由于主特征值與噪聲特征值之間閾值難以設(shè)定，因此采用鄰近奇異值差值法對(duì)源信號(hào)數(shù)進(jìn)行估計(jì)。其以協(xié)方差矩陣的奇異值分解為基礎(chǔ)，計(jì)算得到鄰近奇異值的差值統(tǒng)計(jì)量為

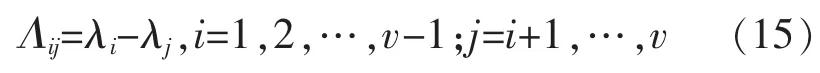
當(dāng) λi和 λj都是噪聲奇異值時(shí)，Λij比較小；λi當(dāng)和λj其中的一個(gè)或兩個(gè)都是信號(hào)奇異值時(shí)，Λij比較大。從最小奇異值開(kāi)始比較，相鄰奇異值差值較大的分界處，就是軸承故障振動(dòng)信號(hào)子空間和噪聲子空間的分界面。從而估計(jì)出軸承故障振動(dòng)源信號(hào)個(gè)數(shù)m。

由政府主導(dǎo)，行業(yè)協(xié)會(huì)指導(dǎo)，跨境電商領(lǐng)軍型企業(yè)牽頭，在共享供應(yīng)鏈的基礎(chǔ)上，以跨境物流聯(lián)盟的形式共建海外倉(cāng)。針對(duì)義烏跨境電商產(chǎn)業(yè)中跨境物流成本高的問(wèn)題，一方面通過(guò)引導(dǎo)義烏中小跨境電商出口企業(yè)在共創(chuàng)品牌提升產(chǎn)品附加值的基礎(chǔ)上提高海外倉(cāng)的應(yīng)用，加強(qiáng)海外倉(cāng)物流信息的可視化和透明化，讓賣家更好掌控物流、運(yùn)營(yíng)、財(cái)務(wù)等狀況；另一方面需要加強(qiáng)規(guī)范化建設(shè)，主動(dòng)為企業(yè)提供海外倉(cāng)政策、法律、稅收等咨詢服務(wù)，提供融資、審批、資格認(rèn)證等政策支持，可通過(guò)政府專項(xiàng)資金幫助義烏中小跨境電商出口企業(yè)體驗(yàn)海外倉(cāng)帶來(lái)的便利和業(yè)績(jī)提升，提升義烏小商品的產(chǎn)品附加值和競(jìng)爭(zhēng)力。

由于EEMD方法分析軸承故障振動(dòng)信號(hào)x（t）所得IMF分量能體現(xiàn)源信號(hào)特征信息，若IMF分量統(tǒng)計(jì)獨(dú)立性越高，則其能夠體現(xiàn)源信號(hào)獨(dú)立成分，越適合用于建立參考信號(hào)。由于互信息是衡量一組隨機(jī)變量之間獨(dú)立性的重要準(zhǔn)則，因此將其當(dāng)作IMF分量選取的準(zhǔn)則。互信息值可以根據(jù)互累積量近似得到［11］，即

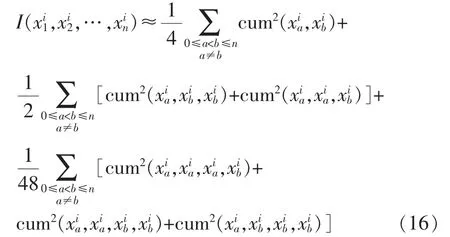
式中：cum（*，*）、cum（*，*，*）、cum（*，*，*，*）分別為xi（t）的二、三、四階互累積量。

通過(guò)計(jì)算IMF分量的歸一化互信息值，根據(jù)估計(jì)的源信號(hào)個(gè)數(shù)m，選取互信息值較小的m個(gè)IMF分量組成參考信號(hào)提取軸承故障振動(dòng)信號(hào)特征。

2.3 信號(hào)特征提取步驟及效果評(píng)價(jià)

對(duì)測(cè)得的軸承故障振動(dòng)信號(hào)進(jìn)行去均值等預(yù)處理，削弱噪聲信號(hào)的影響；利用EEMD對(duì)風(fēng)電機(jī)組軸承故障振動(dòng)信號(hào)x（t）進(jìn)行分解，獲得若干IMF分量；利用鄰近奇異值差值法估算源信號(hào)的個(gè)數(shù)m；根據(jù)式（16）分別計(jì)算各個(gè)IMF分量的歸一化互信息值，選取歸一化互信息值最小的m個(gè)IMF分量建立參考信號(hào)；利用CICA方法提取軸承故障信號(hào)，并進(jìn)行包絡(luò)解調(diào)，得到軸承故障特征。

3 軸承故障實(shí)例分析

3.1 實(shí)例設(shè)計(jì)

本實(shí)例使用來(lái)源于Western Reserve University的軸承故障數(shù)據(jù)［12］。測(cè)試平臺(tái)包括發(fā)電機(jī)、轉(zhuǎn)矩傳感器等設(shè)備，如圖1所示。

圖1 測(cè)試實(shí)驗(yàn)臺(tái)

實(shí)驗(yàn)中，采樣頻率為12 000 Hz，軸承轉(zhuǎn)速為1 749 r／min。軸承具體參數(shù)如表1所示。

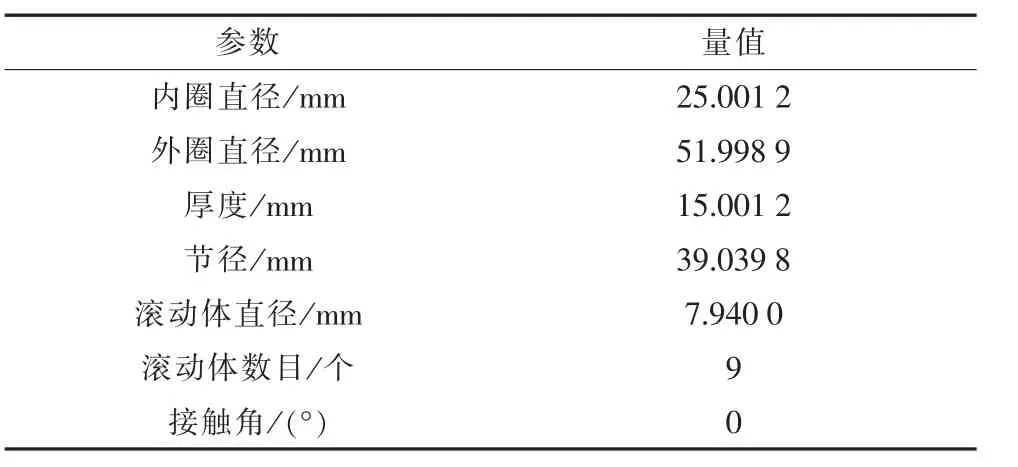
表1 軸承參數(shù)

計(jì)算軸承內(nèi)外圈故障的公式為

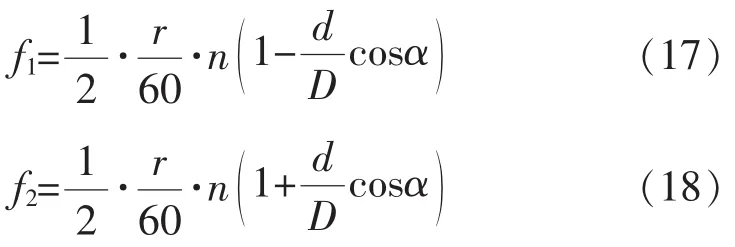
式中：f1、f2分別為內(nèi)圈、外圈故障頻率；r為轉(zhuǎn)速；n為滾動(dòng)體個(gè)數(shù)；d為滾動(dòng)體直徑；D為軸承節(jié)徑；α為接觸角角度。

進(jìn)而，可得軸承正常與故障時(shí)特征頻率，如表2。

表2 軸承特征頻率 Hz

3.2 軸承外圈故障特征提取

主軸承外圈早期故障時(shí)，傳感器采集振動(dòng)信號(hào)，經(jīng)取均值、去噪等預(yù)處理后，到的時(shí)域波形與頻譜如圖2所示。從圖中雖然可以看出故障特征頻率成

分，但幅值相對(duì)較小，不容易分辨。

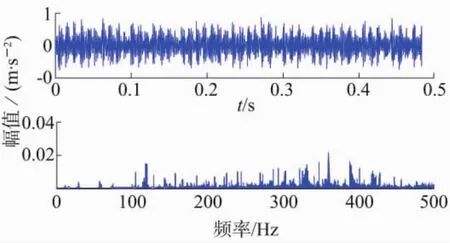
圖2 主軸承外圈故障時(shí)域波形與頻譜圖

對(duì)測(cè)得的主軸承外圈故障信號(hào)x1（t）進(jìn)行EEMD分解，得到 IMF 分量 c1（t），…，c10（t）以及殘余分量r10（t）。 圖 3 表示 x1（t）經(jīng)分解后得到的前 7 階 IMF分量圖。

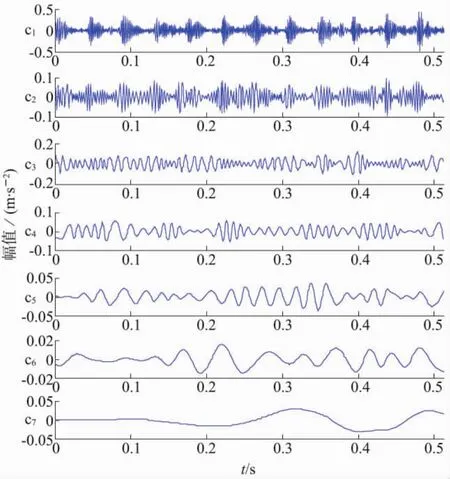
圖 3 IMF 分量（c1～c7）

將故障信號(hào)x1（t）與得到的IMF分量組成新的多維信號(hào) xIME（t）=（x1（t），c1（t），…，c10（t），r10（t）），并進(jìn)一步計(jì)算對(duì)應(yīng)的相關(guān)矩陣然后對(duì)Rx進(jìn)行奇異值分解，得到特征值按照從大到小的順序排列的矢量 Λ=diag｛λ1，…，λ12｝。 根據(jù)鄰近奇異值差值法，計(jì)算相鄰特征值之差，如圖4所示，可知源信號(hào)個(gè)數(shù)為2個(gè)。

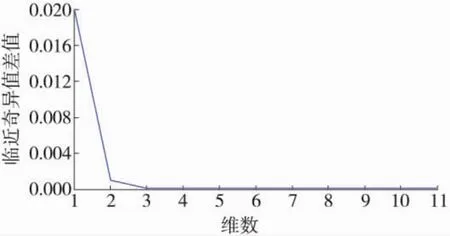
圖4 多維信號(hào)奇異值差值分布

根據(jù)前文所述參考信號(hào)選取方法，選取歸一化互信息值最小的前兩IMF分量作為參考信號(hào)，提取故障數(shù)據(jù)中包含的故障特征，并進(jìn)行包絡(luò)解調(diào)，得到圖5所示包絡(luò)譜。

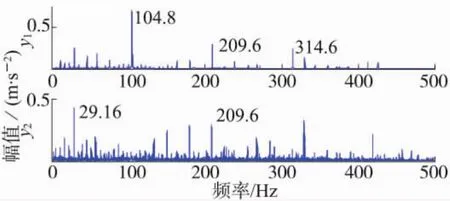
圖5 軸承外圈故障提取信號(hào)包絡(luò)譜

從圖5可以看出，利用所述方法得到的信號(hào)包絡(luò)譜中，在104.8 Hz頻率成分及其二倍頻、三倍頻（209.6 Hz、314.6 Hz）位置處幅值明顯較大，且與計(jì)算所得軸承外圈故障特征頻率值及其倍頻基本一致。據(jù)此，可以得知軸承外圈存在故障。同時(shí)，y2中還包含有軸承的旋轉(zhuǎn)頻率（29.16 Hz），說(shuō)明所提方法同時(shí)也能夠?qū)崿F(xiàn)軸承故障與正常振動(dòng)信號(hào)特征的分離。

3.3 軸承內(nèi)圈故障特征提取

主軸承內(nèi)圈故障時(shí)，傳感器采集振動(dòng)信號(hào)，圖6為經(jīng)預(yù)處理后軸承內(nèi)圈故障時(shí)域波形及頻譜，從圖中也很難辨識(shí)出內(nèi)圈故障特征頻率。

圖6 主軸承內(nèi)圈故障時(shí)域波形與頻譜

與軸承外圈故障特征提取類似，利用本文所提方法得到提取信號(hào)的包絡(luò)譜，如圖7所示。

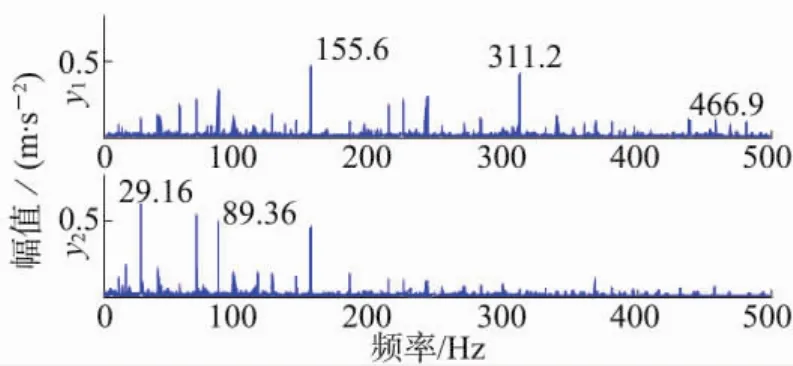
圖7 軸承內(nèi)圈故障提取信號(hào)包絡(luò)譜

從圖7可以看出，在155.6 Hz頻率成分及其二倍頻、三倍頻（311.2 Hz、466.9 Hz）位置處幅值明顯較大，且與計(jì)算所得軸承內(nèi)圈故障特征頻率值及其倍頻基本一致。據(jù)此，可以得知軸承內(nèi)圈存在故障。同時(shí)，軸承內(nèi)圈故障提取信號(hào)y2中也還包含有軸承的旋轉(zhuǎn)頻率（29.16 Hz），以及三倍頻，進(jìn)一步驗(yàn)證所提方法的有效性。

4 結(jié)語(yǔ)

利用基于EEMD和CICA的風(fēng)電機(jī)組軸承故障特征提取方法分別提取軸承外圈、內(nèi)圈故障振動(dòng)信號(hào)中包含的特征信息，并對(duì)提取信號(hào)進(jìn)行包絡(luò)解調(diào)，得到明顯的軸承內(nèi)、外圈故障特征頻率成分。因此，所提方法可以有效突出軸承故障特征信息，實(shí)現(xiàn)對(duì)不同軸承故障特征的有效提取，有利于避免軸承故障的擴(kuò)大。

［1］HAMEED Z，HONG Y S，CHO Y M，et al．Condition monitoring and fault detection of wind turbines and related algorithms：A review［J］．Renewable and Sustainable Energy Reviews，2009，13（1）：1-39．

［2］趙明浩．風(fēng)力機(jī)故障特征分析與實(shí)驗(yàn)研究［D］．北京：清華大學(xué)，2010．

［3］BAFROUI HH，OHADI A.Application of wavelet energy and Shannon entropy for feature extraction in gearbox fault detection under varying speed conditions ［J］.Neurocomputing，2014，133（8）：437-445.

［4］嚴(yán)如強(qiáng)，錢宇寧，胡世杰，等．基于小波域平穩(wěn)子空間分析的風(fēng)力發(fā)電機(jī)齒輪箱故障診斷［J］．機(jī)械工程學(xué)報(bào)，2014，50（11）：9-16．

［5］郭艷平，顏文俊，包哲靜，等．基于經(jīng)驗(yàn)?zāi)B(tài)分解和散度指標(biāo)的風(fēng)力發(fā)電機(jī)滾動(dòng)軸承故障診斷方法［J］．電力系統(tǒng)保護(hù)與控制，2012，40（17）：83－87，93．

［6］林近山．基于經(jīng)驗(yàn)?zāi)Ｊ椒纸夂妥V峭度的滾動(dòng)軸承故障診斷［J］．機(jī)械傳動(dòng)，2012，36（9）：76－79．

［7］胡愛(ài)軍，馬萬(wàn)里，唐貴基．基于集成經(jīng)驗(yàn)?zāi)B(tài)分解和峭度準(zhǔn)則的滾動(dòng)軸承故障特征提取方法［J］．中國(guó)電機(jī)工程學(xué)報(bào)，2012，32（11）：106-111，153.

［8］LU W，RAJAPAKSE J C．Approach and applications of constrained ICA［J］.IEEE Transactions on Neural Networks，2005，16（1）：203．

［9］王志陽(yáng)，陳進(jìn)，肖文斌，等，基于約束獨(dú)立成分分析的滾動(dòng)軸承故障診斷［J］．振動(dòng)與沖擊，2012，31（9）：118－122．

［10］ WEI L，RAJAPAKSE JC．ICA with reference ［J］．Neurocomputing，2006，69（16-18）：2 244-2 257．

［11］ CARDOSO J F．Dependence，correlation and Gaussianity in independent component analysis［J］．Journal of Machine Learning Research，2003，4（4）：1 177-1 203．

［12］ Case Western Reserve University.Bearing data center［EB／OL］．http：／／csegroups.case.edu／bearingdatacenter／pages／，2013－07－15.