純小數加工的心理機制：選擇通達還是平行通達？

孫悅亮 鄭偉意 何先友

(1華南師范大學心理應用研究中心/心理學院/心理健康與認知科學廣東省重點實驗室,廣州 510631)(2韓山師范學院教育科學學院,廣東 潮州 521041)

1 前言

數字的出現是基于人類對計算物體數目的需要。隨著人類社會活動的增加,抽象思維也不斷得到發展,人們發現測量物體時往往會得到不是整數的數,古人就發明了小數來補充整數。小數是十進制分數的一種特殊表現形式。小數由整數部分、小數部分和小數點組成。整數部分是零的小數叫做純小數,整數部分不是零的小數叫做帶小數,例如0.3是純小數,3.1是帶小數。由此可見,小數與整數具有緊密的關系。要全面理解數字的加工與認知,同樣需要關注純小數的加工(Siegler,Thompson,&Schneider,2011;Varma &Schwartz,2011)。

近年來,對數字的認知加工和心理表征吸引了越來越多研究者的興趣。已有一些研究者對整數的認知機制進行了研究,特別是對 10以內的整數的研究更為普遍(Moyer &Landauer,1967;Dehaene,Dupoux,&Mehler,1990)。這些研究為我們認識數字的認知機制提供了很多證據。由于純小數與整數在數的性質上存在一定的差異,因此關于純小數的加工和表征可能也與整數不盡相同。純小數的加工與表征是否也與空間存在關聯,這種關聯與整數與空間的關聯是否相同,整個數字大家族與空間的關聯如何等都是值得探討的問題。

自Dehaene和同事首次發現數字加工和空間認知的關系后(Dehaene,Bossini,&Giraux,1993;Dehaene et al.,1990),數字的空間表征和加工機制一直是數字認知研究的熱點問題。在 Dehaene等(1990)的實驗中,被試的任務是對數字做奇偶判斷,數字的大小是任務不相關的,結果發現,不論是奇數還是偶數,被試對小數字的反應左手要顯著快于右手,而對大數字的反應則是右手顯著快于左手,這種現象被稱為空間?數字反應編碼聯合效應(Spatial Numerical Association of Response Codes,SNARC),這種效應顯示,人們對數字進行加工和表征時,存在一條“心理數字線(Mental Number Line,MNL)”,其方位很可能是自左向右的,小數字表征在心理數字線的左側,大數字則表征在心理數字線的右側。更重要的是,數字加工與空間認知的聯合關系似乎說明了對數字的空間信息的編碼和表征很可能是在較低水平加工,并且是快速和自動完成的(Dehaene et al.,1993;Mapelli,Rusconi,&Umiltà,2003)。此后,很多研究者采用不同的范式和刺激材料更深入地探討了這一效應,結果都一致證明了數字和空間的確存在著編碼聯合效應(Nuerk,Wood,&Willmes,2005;劉超,買曉琴,傅小蘭,2004;Schwarz &Keus,2004;Fischer,Warlop,Hill,&Fias,2004;Gevers,Reynvoet,&Fias,2003)。

Fischer,Castel,Dodd和Pratt (2003)從空間注意的角度對數字加工引起的空間信息的自動激活進行了研究(Fischer et al.,2003),發現僅僅注視數字就會引起空間注意的轉移,當呈現刺激為小數字(1或 2)時,左側刺激的探測要快于右側;當呈現刺激為大數字(8或9)時,右側刺激的探測要快于左側。由此可以看出,數字大小和注意密切相關,大小信息能引起空間注意的分配和轉移,而且注意轉移的方向是由大小數字在心理數字線上的空間位置決定的。

自從 Fischer等(2003)證實空間注意和數字加工的關系以后,對于空間注意如何影響數字加工的研究不斷涌現。Dehaene,Molko,Cohen和Wilson(2004)提出了數字加工的頂葉三回路理論。劉超等(2004)比較了不同注意條件對數字加工的影響,結果發現,注意對大數字和小數字的影響方式是不一樣的：無論是采用內源性線索還是外源性線索,空間注意都在SNARC效應中發揮著重要作用;無論是哪一種注意條件,SNARC效應會隨注意強度的減弱而逐漸弱化,而且外源性注意起到的作用要大于內源性注意,這表明自下而上的自動化注意對SNARC效應起主要作用。這與Fischer等(2003)的研究一致,即SNARC效應的發生是一種自動化的過程。

上述研究從不同角度探討了數字加工和表征與空間表征的關系,但對純小數的認知加工和表征及其與空間表征的關系還不很清楚。先前對數字加工和表征的研究關注了自然數(整數、正數和負數),特別是對 10以內的整數的研究,但尚未涉及小數,然而這些研究為探索小數加工的機制提供了重要的啟示。

先前對自然數的表征和加工研究,一方面關注大小比較中一位自然數和多位自然數的連續性和分離性問題,并提出了連續性假說(continuous hypothesis)和分離假說(discrete hypothesis);另一方面從語義和語法的角度關注十進制中的位置值符號系統(place-value symbol system)在命名大量數字時所帶來的語義和語法的干擾效應對位置值成分加工(place-value components processed)的影響(Moyer &Landauer,1967;Nuerk,Weger,&Willmes,2001;Korvorst &Damian,2008)。

連續性假說認為數字1～9所具有的量級大小在心理上是通過距離效應來進行表征：比較一對數字的大小時,二者的量級差異越大,反應時間越快。比如人們比較1和9的速度要快于1和3的速度。分離假說認為十進制數字是以結構的形式來表征：基于十進制數字符號系統和具體化的語法表達。十進制數字符號結構的語義意義是通過語義數位值成分中的語法結構規律來呈現和計算的。比如,“29”被表征為十位是 2、個位是 9的結構,它是由十進制算法所計算出來的。

以往對自然數大小比較的研究驗證了上述兩種假說,一位自然數在心理加工過程中具有連續的量級大小表征(Moyer &Landauer,1967),多位自然數的大小比較是被分離表征的,而且其數位價值成分(place-value components)是平行加工的(Hinrichs,Berie,&Mosell,1982;Poltrock &Schwartz,1984;Wood,Mahr,&Nuerk,2005;Korvorst &Damian,2008)。比如人們比較21和87時相對更快,因為十位數上2小于8,因而21小于87,個位數的1也小于7,因此21小于87。相反,在比較29和83時反應相對較慢,因為十位數產生的判斷是 2小于 8,而個位數會產生 9大于 3,二者存在一定的沖突,因此反應時延長。

由于純小數與整數在數的性質上存在一定的差異,先前研究未能涉及純小數的數位價值成分平行加工問題。直至2013年,Varma等人采用大小比較任務首次對純小數的加工與空間表征的關系進行了研究,該研究的意義在于：首先,Varma和Karl(2013)在綜述先前自然數的表征和加工研究成果基礎上,從純小數的語義和語法關系角度論述了純小數表征和加工的選擇通達假說(elective access hypothesis)和平行通達假說(parallel access hypothesis)。選擇通達假說認為,純小數的加工與表征只激活了一個正確的指示物(referent),并且這個指示物就是純小數本身。與之相反,平行通達假說認為,純小數的加工與表征同時激活了正確的和不正確的指示物,即不僅激活了純小數本身,同時還激活了小數點右邊的自然數。平行通達假說支持語義干擾效應,即當純小數的加工與表征同時激活了正確的和不正確的指示物時會產生沖突的判斷,導致反應時變慢,如比較 0.2和 0.87會相對較快,因為0.2小于0.87,2小于87,而0.27和0.9的判斷會更慢,因為 0.27小于 0.9,而 27大于 9。其次,Varma和 Karl (2013)的研究結果發現,純小數的大小表征存在語義干擾效應(semantic interference effect),語義干擾效應的發現證明了平行通達假說,而不是選擇通達假說;同時,純小數也存在SNARC效應。

因此,Varma和Karl (2013)的研究拓展了數字的加工與認知研究領域,為探索純小數加工的機制提供了重要的證據和啟示。正是基于Varma和Karl(2013)研究的啟示和對純小數加工的機制的探究,啟發我們改進研究范式,從而對純小數的加工及其與空間表征的聯系進行深入研究。

已有研究認為,任務要求可能影響數字表征,特定的任務要求可能誘導被試產生不同的表征(B?chtold,Baumüller,&Brugger,1998;Fischer &Rottmann,2005;Hung,Humg,Tzeng Ovid,&Wu,2008;Lindemann,Abolafia,Pratt,&Bekkering,2008;Shaki &Fischer,2008;Shaki &Petrusic,2005)。要探究不同符號數字以及非數字信息的空間表征機制,自動加工范式有其獨特優勢,這可以使線索信息的加工不會受到任務要求和有意反應策略的影響(Kadosh,2008;Kadosh,Henik,&Rubinsten,2008;Tzelgov &Ganor-Stern,2004)。自動化加工可以給探究表征機制問題提供一種更好的途徑(Ganor-Stern &Tzelgov,2008;Ganor-Stern,Tzelgov,&Ellenbogen,2007)。Tzelgov和 Ganor-Stern (2004)認為,當數字被自動加工而且被試按要求無意識完成實驗任務時,可以更好地對心理表征進行探測,因此,為了解數字心理表征的基本特征,應該使用把有意策略最小化的實驗范式。

盡管Varma和Karl (2013)對純小數的加工和表征的研究取得了意義重大的結論,但由于Varma和Karl (2013)的研究使用的實驗任務屬于有意控制任務,被試的反應可能受到自身的有意反應策略的影響,而且,大小判斷等二分類別判斷可能產生言語編碼,進而影響了數字自動表征的結果。因此,我們認為,使用有意策略最小化的實驗范式可以更好的探究純小數的加工及其與空間表征的聯系,研究結論將為純小數的加工與表征機制提供新的研究證據。

因此,本研究采用 Dodd等(Dodd,van der Stigchel,Leghari,Fung,&Kingstone,2008)使用的目標覺察范式(該實驗范式中實驗任務與考察目標無關,而且實驗任務完成過程中排除了其他認知過程),對純小數的加工及其與空間表征的聯系進行深入研究。本研究設計了3個實驗,探討純小數的加工是否能引起空間注意的SNARC效應,從而探討純小數的通達方式。實驗 1采用目標覺察范式(Dodd et al.,2008),使用純小數和小數點后自然數的數量大小判斷一致的材料,探討純小數作為線索時是否可以引起空間注意的SNARC效應。研究邏輯是,如果純小數能夠誘發注意的空間轉移,那么在目標覺察任務中,純小數大小表征會影響空間目標覺察反應,就會引發注意 SNARC效應,則支持平行通達假設。實驗2探討數量值大小相同但表達方式不同的純小數能否引起注意的SNARC效應。研究邏輯是,如果純小數的加工符合平行通達假說,即同時激活了純小數本身及小數點右邊的自然數,那么在數量值大小相同但表達方式不同的純小數之間就會出現注意 SNARC效應,則支持平行通達假說。反之,如果純小數的加工符合選擇通達假說,即只是激活了純小數本身,則不會出現注意 SNARC效應。實驗3比較純小數的加工對小數本身及對應的自然數激活強度的大小。研究邏輯是,在純小數本身大小判斷與對應自然數大小判斷不一致的條件下,如果純小數的加工同時激活了純小數本身及小數點右邊的自然數,并且純小數本身與小數點右邊的自然數激活強度一樣大時,那么不會出現注意SNARC效應,則支持平行通達假設;如果純小數本身的激活強度與小數點右邊的自然數不一樣,則會出現注意SNARC效應,則支持選擇通達假說。

2 實驗1 純小數引發的注意SNARC效應研究

2.1 實驗目的

采用目標覺察范式,使用純小數和小數點后自然數的數量大小判斷一致的材料,探討純小數作為線索時是否可以引起空間注意的轉移。

2.2 研究方法

2.2.1 被試

選取20名右利手被試,其中男8名,女12名,視力或矯正視力正常,完成實驗給予適當的報酬。被試來自華南師范大學的在校本科生或研究生,平均年齡22歲,母語為漢語。

2.2.2 實驗材料

4個純小數：0.17,0.27,0.83,0.93作為刺激材料的提示線索,隨機出現于探測刺激之前。4個純小數組成數量的兩個水平：小(0.17,0.27);大(0.83,0.93)。探測刺激是視角為4°的黑色方塊。

2.2.3 實驗設計

實驗采用2×2×4完全組內設計。3個自變量分別是：(1)線索類型：數值小和數值大;(2)探測刺激位置：左邊(目標出現在注視點的左邊)和右邊(目標出現在注視點的右邊);(3)SOA (延遲)：100 ms、250 ms、500 ms和750 ms。實驗因變量為目標覺察的反應時和反應錯誤率。實驗中的控制變量為反應手和刺激呈現位置。要求被試使用右利手進行按鍵反應。

2.2.4 實驗程序

實驗在保持日光燈照明的房間內進行,被試坐在距離計算機屏幕60 cm左右處,按鍵盤空格鍵作反應。實驗的刺激材料呈現于聯想 17寸彩色顯示器,刷新頻率為100 Hz,分辨率為1024×768。

實驗中每個trial從中央注視點(圓點,黑色,直徑為0.3°視角)開始,在注視點水平左右各有1個白色的正方形方框,方框的直徑 1.5°視角,其中左右方框到注視點的距離為4°視角,作為實驗材料呈現在黑色背景的計算機屏幕上,實驗流程如圖1所示。

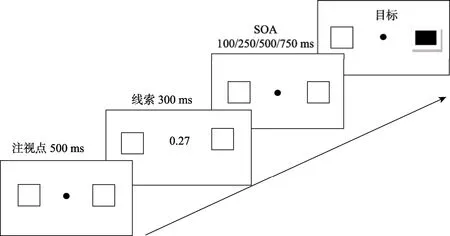
圖1 實驗流程圖示

首先在白色屏幕正中呈現一個視角為0.3°的注視點(黑色圓點)500 ms,不采用“+”為注視點字是為了避免實驗中被試將“+”看成或聯想到“十”,而對實驗結果產生污染。實驗要求被試凝視中央的注視點,并且眼睛不要移動;然后注視點被數字(黑色,視角為0.8°)取代,其中不同大小的純小數隨機出現在中央注視點位置,每個數字出現的概率相同,呈現的時間均為300 ms。指導被試忽視呈現在注視點的數字,這些數字和實驗任務無關,并且不能預測即將出現的目標的位置;隨后在注視點處出現一個0.3°視角的黑色圓點,持續時間分別為100 ms、250 ms、500 ms或750 ms,不同的持續時間隨機變化,以避免被試的習慣性反應;隨后在屏幕左右視野兩個方框之一中出現黑色的方塊(方框的直徑為1.5°視角),方塊出現在左右空間視野是隨機的,但是呈現的概率相等,呈現的方塊持續的時間由被試控制,按鍵反應進入下一個界面;指導被試當其覺察到目標時就盡可能快的按空格鍵作反應。為了避免提早發生反應,線索?目標 SOA在 trials中是隨機變化的。反應小于100 ms或者長于1000 ms被認為是做了錯誤反應,在練習階段給予反饋;被試按鍵反應之后,出現黑色的緩沖界面,持續時間為500 ms,隨后是下一輪trial。

2.3 結果與分析

使用SPSS 17.0對數據進行統計分析。反應時短于100 ms或長于1000 ms的反應被認為是做了錯誤的反應,所有trials錯誤率小于2%,這些錯誤trials在隨后的進一步分析中被排除。實驗結果采用2(探測刺激位置：左邊和右邊)× 2(線索類型：數字數量值小和大)× 4(SOA延遲：100 ms,250 ms,500 ms,750 ms)的重復測量方差分析。

不同條件下目標覺察的反應時與標準差見表1,分析結果表明,SOA的主效應顯著,

F

(3,17)=19.88,

p

<0.001,η=0.41,1?β=0.996;其他主效應不顯著,

p

>0.05;位置×數值×延遲的三重交互作用顯著,

F

(3,57)=12.73,

p

<0.01,η=0.31,1?β=0.991,如圖2所示。當探測刺激前的提示線索為數量值大的數字(0.83,0.93),數字提示線索與探測刺激之間的延遲為 500 ms時,被試對右側目標刺激的探測顯著快于左側,

F

(1,19)=6.51,

p

<0.001,η=0.20,1?β=0.997;當探測刺激前的提示線索為數量值小的數字(0.17,0.27)時,當數字提示線索與探測刺激之間的延遲為 500 ms時,被試對左側刺激的識別要快于右側,

F

(1,19)=4.79,

p

<0.001,η=0.18,1?β=0.989;在其他延遲時間均沒有發現顯著差異(

p

>0.05)。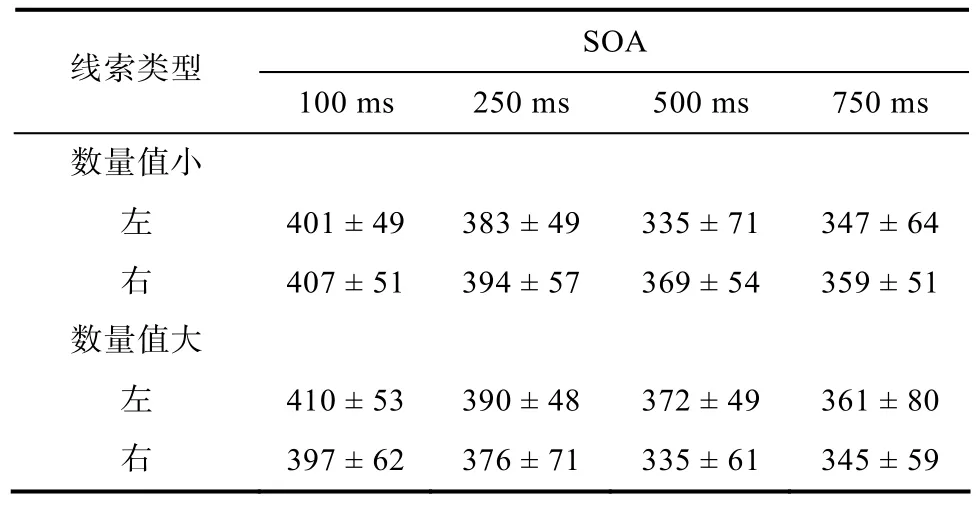

表1 不同條件下目標覺察的平均反應時(M ± SD)

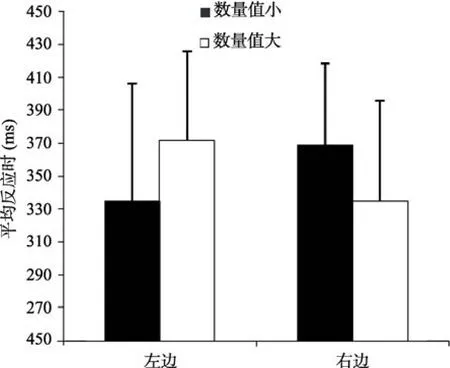
圖2 純小數數量值大小與探測刺激位置的交互作用

實驗1的結果顯示,純小數的加工和表征與空間存在關聯,能夠引起空間注意的轉移。這一結果表明,被試的心理表征中存在一條表征純小數數量值的心理數字線,數量值小的小數表征在心理數字線的左側,數量值大的純小數表征在心理數字線的右側。在500 ms時,純小數大小與探測刺激方向的交互作用效應顯著,這一研究結果和先前研究者用其他數字作為材料得到的結果一致(Fischer et al.,2003;Dodd et al.,2008)。

據此,我們還不能認為,純小數的加工可以自動地引起基于純小數真實數量大小的空間注意的轉移。因為按照Varma和Karl (2013)年提出的平行通達假說,純小數在大小加工時會同時激活純小數點右邊的自然數,在實驗 1的材料中,每一個純小數對于純小數本身的數量大小和對于對應自然數大小判斷是一致的(比如 0.27對應 0.93判斷為小,27對應93判斷也為小),因此我們不能確定此時的空間注意轉移是由純小數本身的數量大小還是同時激活的自然數大小引起的。以往研究結果表明,自然數大小可以引起空間注意的轉移(Fischer et al.,2003;Dehaene et al.,2004;劉超等,2004;Casarotti,Michielin,Zorzi,&Umilta,2007),因此,我們要解決這一問題,就需要先確定純小數的大小加工是否激活了純小數點右邊的自然數。

3 實驗 2 表達方式不同但數值相同的純小數引發的注意 SNARC效應研究

3.1 實驗目的

探討數量值大小相同但表達方式不同的純小數能否引起注意的 SNARC效應,進一步驗證純小數的加工是否符合平行通達假說。

3.2 研究方法

3.2.1 被試

選取20名右利手被試,其中男6名,女14名,視力或矯正視力正常,完成實驗給予適當的報酬。被試來自華南師范大學的在校本科生或研究生,平均年齡22歲,母語都是漢語,而且被試沒有參加過實驗1。

3.2.2 實驗材料

4個純小數：0.2,0.20,0.3,0.30作為刺激材料的提示線索,隨機出現于探測刺激之前。探測刺激為白色背景上的黑色方塊。4個純小數分成百分位無0 (0.2,0.3)和百分位有0 (0.20,0.30)兩個水平。探測刺激是視角為4°的黑色方塊。

3.2.3 實驗設計

實驗采用2×2×4完全組內設計。3個自變量分別是：(1)線索類型：百分位無0和百分位有0;(2)探測刺激位置：左邊(目標出現在注視點的左邊)和右邊(目標出現在注視點的右邊);(3)SOA延遲：100 ms、250 ms、500 ms和750 ms。實驗因變量為目標覺察的反應時和反應錯誤率,實驗中的控制變量為反應手和刺激呈現位置。要求被試使用右利手進行按鍵反應。

3.2.4 實驗程序

實驗程序同實驗1。

3.3 結果與分析

使用SPSS 17.0對數據進行統計分析。反應時短于100 ms或長于1000 ms的反應被認為是做了錯誤的反應,所有 trials錯誤率小于 1.8%,這些錯誤 trials在隨后的進一步分析中被排除。實驗結果采用2(探測刺激位置：左邊和右邊)× 2(線索類型：百分位有0和百分位無0)× 4(SOA延遲：100 ms,250 ms,500 ms,750 ms)的重復測量方差分析。

不同條件下的平均反應時和標準差見表2,分析結果表明,數字類型的主效應顯著,

F

(1,19)=65.87,

p

<0.01,η=0.70,1?β=0.997;SOA 的主效應顯著,

F

(3,17)=17.78,

p

<0.01,η=0.38,1?β=0.995。其他主效應不顯著,

p

>0.05;更重要的是,位置×數字×延遲的三重交互作用顯著,

F

(3,57)=13.10,

p

<0.01,η=0.33,1?β=0.965,如圖3所示。當探測刺激前的提示線索為百分位有 0(0.20,0.30),探測刺激之間的延遲為 500 ms時,被試對右側目標刺激的探測顯著快于左側,

F

(1,19)=9.52,

p

<0.001,η=0.18,1?β=0.998;當探測刺激前的提示線索為百分位無 0 (0.2,0.3),數字提示線索與探測刺激之間的延遲為 500 ms時,被試對左側刺激的識別要快于右側,

F

(1,19)=5.81,

p

<0.001,η=0.13,1?β=0.987;在其他延遲時間均沒有發現顯著差異(

p

>0.05)。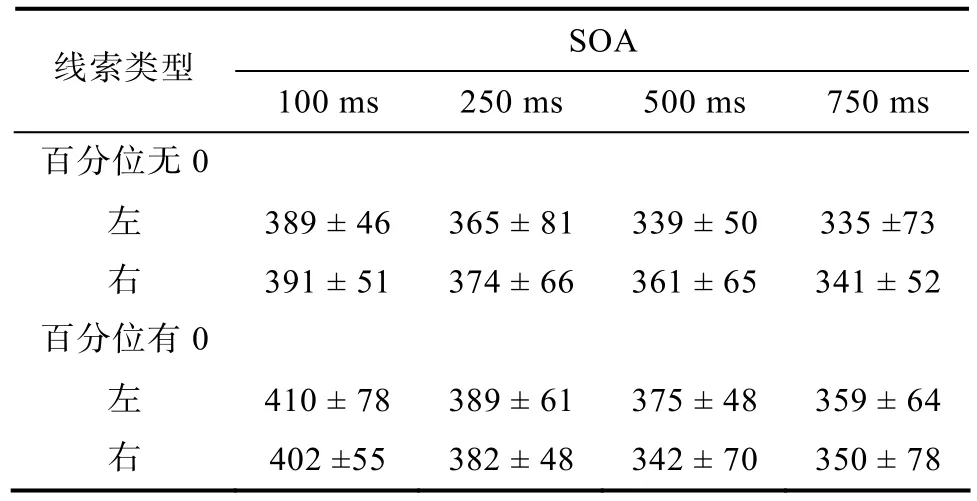

表2 不同條件下目標覺察的平均反應時(M ± SD)

實驗2的結果顯示,左右兩側探測刺激的探測速度出現顯著差異的時間仍然為 500 ms,重復了實驗1的結果,這說明對小數點右邊的自然數的激活是自動、快速的。據此,我們可以說,純小數在大小表征時是同時激活了純小數本身和小數點右邊的自然數,這個結果與平行通達假說預期一致。

由于我們采取的是兩組數量值大小相同但是表達式不同的純小數的提示線索,但在這種實驗條件下,如果被試覺得對小數點和小數點左邊的0的加工是沒有意義的,被試就會忽視小數點和小數點左邊的0,從而只對小數點右邊的自然數進行加工,如果真是這樣,我們仍不能確定平行通達假設的合理性。因此,還有一個問題需要解決,即對小數點右邊的自然數激活程度如何,是與純小數本身一樣大還是比純小數本身激活程度更大。

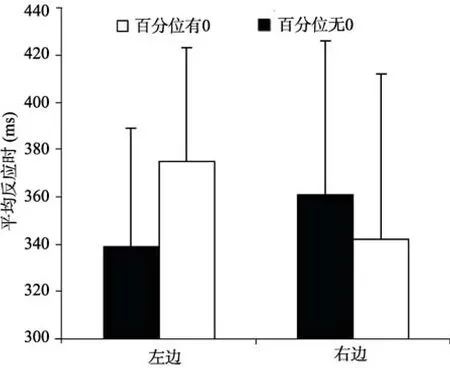
圖3 純小數數字類型與探測刺激位置的交互作用

4 實驗 3 純小數加工對小數本身及對應的自然數激活強度的比較

4.1 實驗目的

實驗2中得到的對純小數加工引起的空間注意的轉移是否是真正的對純小數作為整體進行了加工呢？純小數的加工對小數本身及對應的自然數激活強度如何？這些問題還需要進一步探討。實驗3通過選取特殊的材料,將純小數本身大小判斷與對應的自然數大小判斷沖突的兩組純小數混合在一起作為實驗材料的提示線索,進一步探討純小數加工。

4.2 研究方法

4.2.1 被試

選取20名右利手被試,其中男8名,女12名,視力或矯正視力正常,完成實驗給予適當的報酬。被試來自華南師范大學的在校本科生或研究生,平均年齡23歲,母語都是漢語,而且被試沒有參加過實驗1和實驗2。

4.2.2 實驗材料

4個純小數：0.17,0.27,0.8,0.9作為刺激材料的提示線索,隨機出現于探測刺激之前。探測刺激為白色背景上的黑色方塊。4個純小數分成數量小但自然數大(0.17,0.27)和數量大但激活的自然數小(0.8,0.9)兩個水平。探測刺激是視角為4°的黑色方塊。

4.2.3 實驗設計

實驗采用2×2×4完全組內設計。3個自變量分別是：(1)線索類型：數量小但自然數大(0.17,0.27)和數量大但激活的自然數小(0.8,0.9);(2)探測刺激位置：左邊(目標出現在注視點的左邊)和右邊(目標出現在注視點的右邊);(3)SOA延遲：100 ms、250 ms、500 ms和750 ms。實驗因變量為目標覺察的反應時和反應錯誤率。實驗中的控制變量為反應手和刺激呈現位置。要求被試使用右利手進行按鍵反應。

4.2.4 實驗程序

實驗程序同實驗1、實驗2

4.3 結果與分析

使用SPSS 17.0對數據進行統計分析。反應時短于100 ms或長于1000 ms的反應被認為是做了錯誤的反應,所有trials錯誤率小于2%,這些錯誤trials在隨后的進一步分析中被排除。實驗結果采用2(探測刺激位置:左和右)× 2(線索類型:數量值小和數量值大)× 4(SOA延遲：100 ms,250 ms,500 ms,750 ms)的重復測量方差分析。

不同條件下的平均反應時和標準差見表3,分析結果表明,純小數數量大小的主效應顯著,

F

(1,19)=74.97,

p

<0.05,η=0.53,1?β=0.748;SOA的主效應顯著,

F

(3,17)=19.53,

p

<0.01,η=0.32,1?β=0.992。數字的數量大小與探測刺激呈現位置交互作用不顯著,

F

(3,17)=16.20,

p

>0.05,η=0.04,1?β=0.266。

表3 不同條件下目標覺察的平均反應時(M ± SD)

實驗3的結果顯示,純小數大小加工沒有引起空間注意的轉移,被試并沒有形成像實驗1或實驗2一樣的心理數字線。這個結果可以很好的回答實驗2所產生的疑問。因為在實驗3的條件下,如果被試只對小數點右邊的自然數進行加工,那么實驗結果應該出現經典的注意SANRC效應,即我們可以得到一條與實驗 1中形成的不同的心理數字線,這條線并沒有按照純小數的實際數量值大小進行排列,而正好相反,本身數量值小的純小數(如,0.27對應得到的自然數為 27,比 9大)排在數字線的右端,數量值大的純小數(如,0.9對應得到的自然數為 9,比 27小)排在數字線的左端。說明被試對純小數的大小判斷出現了沖突,這個沖突導致了被試不能形成一條清晰的心理數字線。這個結果說明了實驗2的結論是正確的,純小數在大小表征時同時激活了純小數本身和小數點右邊的自然數。同時實驗3也再次證明了平行通達假說的合理性。

實驗3結果表明,純小數的加工與表征對本身與對應的自然數激活強度是一樣的。在時間進程上,3種延遲條件都沒有出現顯著差異,這主要與實驗任務有關。我們的實驗任務使得被試只是對純小數進行了低水平的加工,并沒有讓被試最終對純小數的真實數量大小做出判斷,這和 Varma和 Karl(2013)的研究是不一樣的。Varma和Karl (2013)使用的是大小判斷任務來研究純小數的加工和表征,在這種實驗任務下,被試雖然會因為純小數本身的大小判斷和激活的自然數的大小判斷出現了沖突導致反應時間加長,但最終被試還是會對純小數真實的數量大小進行了判斷,使得實驗結果出現經典的SNACR效應。

5 討論

本研究采用不同的數字組作為提示線索,采用目標覺察范式(Dodd et al.,2008),探討了純小數的加工與表征是否也與空間存在關聯,是否也可以引起空間注意的轉移,產生空間注意的轉移原因是基于純小數的數量大小還是同時與純小數點后面的自然數有關,以及可能形成的心理數字線,從而進一步驗證平行通達假說的正確性。

實驗1發現,在中央注視點位置呈現大小判斷一致的純小數能夠自動誘發注意的 SNARC效應,當呈現數量值較小的純小數時,發現左側的刺激探測要顯著快于右側;當呈現數量值較大的純小數時,右側的刺激探測要顯著快于左側。值得注意的是,在實驗中,雖然明確告知被試呈現在固定點的數字線索信息與實驗的目標覺察任務無關或者不能提供什么信息,即意味著純小數本身與任務沒有直接的聯系,但實驗結果還是觀察到純小數線索能夠自動地誘發注意空間轉移,并且影響到隨后目標的覺察。Kadosh等(2008)認為,分析自動加工(即數字加工與任務無關時)是了解內部表征本質的一種更好的方法,因此本實驗更好地說明了純小數的空間表征機制。

實驗2是將數量值大小相同但是表達式不同的純小數作為探測刺激前的線索,當呈現百分位無 0(如0.2,0.3)的純小數時,發現左側刺激識別要顯著快于右側;當呈現百分位有 0的純小數(如 0.20,0.30)時,右側刺激探測要顯著快于左側。這表明空間注意的轉移是基于小數點后面的自然數而不是純小數的真實數量大小。綜合實驗1和實驗2的研究結果可以看出,純小數在大小加工時會同時激活小數點右邊的自然數,驗證了Varma和Karl (2013)提出的平行通達假說。

實驗3進一步驗證了Varma和Karl (2013)提出的平行通達假說,同時說明被試對于純小數是作為一個整體進行自動化加工的,并沒有出現忽視小數點及小數點左邊的0的情況。實驗3中我們將純小數本身大小判斷與對應的自然數大小判斷沖突的純小數作為探測刺激前的線索,該條件下我們并沒有得到由有效提示線索所引發的對數字數量大小加工引起的空間注意的轉移。這說明被試對純小數的大小判斷出現了沖突,這個沖突導致了被試不能在心理形成一條清晰的心理數字線。

5.1 純小數的加工及表征與空間的關聯問題

在3個實驗中,我們通過呈現不同類型的數字組作為提示線索,兩個實驗結果發現,純小數的加工引發了空間注意的轉移,說明純小數的加工與空間存在關聯,能夠引起空間注意的轉移。但在目標覺察范式中,究竟是對純小數整體的加工還是部分的加工引起了空間注意的轉移呢？純小數與分數、負數一樣相對于自然數屬于更抽象的數字,在他們的表達式里含有一定的數學符號,這些數學符號會不會影響到空間注意的轉移呢？Shaki和 Petrusic(2005)針對負數的心理表征提出了數量?極性假說(Magnitude-Polarity Hypothesis),他們認為負數的心理表征取決于任務設置以及任務的需求：若個體在提前獲知需要加工負數或者正數的條件下,會優先加工數字數量,而后加工數量的極性(正或負),此時負數的心理表征由其絕對值決定,形成的心理數字線也僅僅按照負數的絕對值部分將其排列在心理數字線上;反之,若個體在未提前獲知的條件下,符號和數量會作為一個整體同時得到加工,負數的心理表征由實際數量值決定,形成的心理數字線也會相應地按照負數的實際數量值將其排列在數字線上。張宇和游旭群(2012)采用刺激探測任務研究了負數加工,得到了與Shaki和Petrusic (2005)采用大小比較任務一致的結果。

在本研究中,我們必須排除這種可能：當所有的數字都為純小數時,由于數字與反應任務無關,被試會迅速適應于所有的提示線索數字都是純小數,并且對數字每次出現在屏幕的位置也會熟悉,進而形成預期,因此純小數的小數點和小數點左邊的0都會變得對純小數加工沒有意義,從而被試會忽視純小數點和小數點左邊的 0,而只對純小數點右邊的自然數進行加工。在實驗2中,我們采取的是兩組數量值大小相同但是表達式不同的純小數的提示線索,在這種條件下,如果被試覺得對小數點和小數點左邊的0的加工是沒有意義的,被試就會忽視小數點和小數點左邊的 0,從而只對純小數點右邊的自然數進行加工,這樣也有可能引起空間注意的轉移,如果真是這樣,我們將不能確定實驗得到的空間注意轉移是被試僅僅對自然數部分進行了加工還是對純小數整體進行了加工引起的。

然而,通過實驗 3,我們可以確定在本實驗范式下,被試對純小數進行了整體的加工。因為在實驗3條件下,如果被試只對小數點右邊的自然數進行加工,那么實驗結果應該出現經典的注意SANRC效應,即我們可以得到一條與實驗 1中形成的不同的心理數字線,這條線并沒有按照純小數的實際數量值大小進行排列,而正好相反,本身數量值小的純小數(如,0.27對應得到的自然數為 27,比9大)排在數字線的右端,數量值大的純小數(如,0.9對應得到的自然數為9,比27小)排在數字線的左端。實驗3的結果說明了實驗1、實驗2的所得到的空間注意的轉移是由被試對純小數整體的加工引起的。但是,與其他數字不同的是,純小數的空間注意轉移的方向同時受到純小數本身以及對應的自然數的影響,當純小數本身與空間關聯的方向與對應的自然數的空間關聯方向一致時,被試能夠形成心理數字線,結果產生注意的SNARC效應;當純小數本身與空間關聯的方向與對應的自然數的空間關聯方向不一致時,在本實驗任務下,被試不能夠形成心理數字線,結果沒有出現注意的SNARC效應。

5.2 純小數的加工是否同時激活了純小數及小數點右邊的自然數問題

關于純小數的加工存在著兩種不同的假說。選擇通達假說認為,純小數的加工只激活了一個指示物,并且這個指示物就是純小數本身。與之相反,平行通達假說認為,純小數的加工與表征不僅激活了純小數本身,同時還激活了小數點右邊的自然數。Varma和Karl (2013)在大小比較任務中發現了語義沖突效應：當純小數本身和小數點右邊的自然數的大小判斷出現沖突時,被試的反應時加長。比如,0.2和0.87的大小判斷應該比較快,因為純小數本身和小數點右邊的自然數的大小判斷是一致的(0.2 <0.87,2 <87),而0.27和0.9的大小判斷應該比較慢,因為純小數本身和小數點右邊的自然數的大小判斷出現了沖突(0.27 <0.9,27 >9)。語義沖突效應的發現證明了純小數的加工和表征采取的是平行通達方式。然而,我們認為,Varma和 Karl(2013)使用的實驗任務屬于有意控制任務,被試的反應可能受到自身的有意反應策略的影響。而且,大小判斷等二分類別判斷可能產生言語編碼,進而影響了數字自動表征的結果。大小比較任務中一致性效應可能被言語因素驅動,言語表征可能會影響實驗任務的完成(Nuerk,Bauer,Krummenacher,Heller,&Willmes,2005)。因此,如果要探究數字的空間表征機制,使用自動加工范式有其重要的優勢,其可以讓線索信息的加工不會受到任務要求和有意反應策略的影響(Kadosh,2008;Kadosh et al.,2008;Tzelgov &Ganor-Stern,2005)。我們改進了實驗方式,采用了目標覺察范式(Dodd et al.,2008)來探究純小數的空間表征中是否存在注意 SNARC效應,以此驗證純小數的空間表征是否激活了純小數本身和小數點右邊的自然數。目標覺察范式的實驗任務與考察目標無關,這樣可以更好的探究數字空間表征的內部機制以及數字誘發的相關效應。在實驗2中,我們得到了注意的 SNARC效應,究其原因,我們認為是純小數的加工和表征不僅激活了純小數本身,同時還激活了小數點右邊的自然數,在純小數本身的數量大小一致的情況下,基于純小數激活的不同自然數數量大小加工引起了空間注意轉移。據此,我們認為純小數的加工和表征采取的是平行通達方式。

5.3 本研究的不足與未來研究

本研究雖然使用目標覺察范式驗證了平行通達假說的正確性。但是對于純小數的加工與表征為什么會同時激活純小數本身以及純小數點右邊的自然數還沒能進行探究。純小數的概念更多是來自人們后天的學習和練習,并且在純小數的學習與練習中,我們還會不斷的使用到整數的法則。例如,純小數大小的比較方法與整數基本相同,即從高位起,依次把相同數位上的數加以比較。這導致了純小數和整數一樣在進行大小比較的時候會出現句法沖突效應(Nuerk et al.,2001;Varma &Karl,2013)。正是因為人們進行純小數大小比較的時候使用了整數的法則,可能使得人們在加工和表征純小數時習慣性的激活了相應的整數,最終出現了語義沖突效應(Varma &Karl,2013)。如果純小數本身的激活與對應的自然數激活強度確實一樣,那么,二者是否會隨著人們對數字學習程度的變化而發生變化呢？個體對數字的學習一般都是先整數后小數,因此,未來的研究可以從發展的角度進一步探討該問題。

6 結論

本研究采用策略性更小的目標覺察范式,探討了純小數加工及其與空間表征的聯系,結果發現：(1)純小數的加工可以引起空間注意的轉移,即產生注意的SNARC效應;純小數加工采取的是平行通達的方式。這一結論與前人研究基本一致。(2)本研究同時發現,純小數的加工會同時激活純小數本身和對應的自然數,并且對應自然數的激活強度與純小數本身一樣大,這是一種整體自動化的加工;純小數引發的空間注意的轉移方向同時受到純小數本身以及對應的自然數的影響。

B?chtold,D.,Baumüller,M.,&Brugger,P.(1998).Stimulus-response compatibility in representational space.

Neuropsychologia,36

,731?735.Casarotti,M.,Michielin,M.,Zorzi,M.,&Umilta,C.(2007).Temporal order judgment reveals how number magnitude affects visuospatial attention.

Cognition,102

,101?117.Dehaene,S.,Bossini,S.,&Giraux,P.(1993).The mental representation of parity and number magnitude.

Journal of Experimental Psychology:General,122

,371?396.Dehaene,S.,Dupoux,E.,&Mehler,J.(1990).Is numerical comparison digital? Analogical and symbolic effects in two-digit number comparison.

Journal of Experimental Psychology:Human Perception and Performance,16

,626?641.Dehaene,S.,Molko,N.,Cohen,L.,&Wilson,A.J.(2004).Arithmetic and the brain.

Current Opinion in Neurobiology,14

,218?224.Dodd,M.D.,van der Stigchel,S.,Leghari,M.A.,Fung,G.,&Kingstone,A.(2008).Attentional SNARC:There’s something special about numbers (let us count the ways).

Cognition,108

,810?818.Fischer,M.H.,Castel,A.D.,Dodd,M.D.,&Pratt,J.(2003).Perceiving numbers causes spatial shifts of attention.

Nature Neuroscience,6

,555?556.Fischer,M.H.,&Rottmann,J.(2005).Do negative numbers have a place on the mental number line?

Psychology Science,47

(1),22?32.Fischer,M.H.,Warlop,N.,Hill,R.L.,&Fias,W.(2004).Oculomotor bias induced by number perception.

Experimental Psychology,51

(2),91?97.Ganor-Stern,D.,&Tzelgov,J.(2008).Across-Notation Automatic Numerical Processing.

Journal of Experimental Psychology:Learning,Memory,and Cognition,34

(2),430?437.Ganor-Stern,D.,Tzelgov,J.,&Ellenbogen,R.(2007).Automaticity and two-digit numbers.

Journal of Experimental Psychology:Human Perception and Performance,33

,483?496.Gevers,W.,Reynvoet,B.,&Fias,W.(2003).The mental representation of ordinal sequences is spatially organized.

Cognition,87

,B87?B95.Hinrichs,J.V.,Berie,J.L.,&Mosell,M.K.(1982).Place information in multidigit number comparison.

Memory &Cognition,10

,487?495.Hung,Y.H.,Hung,D.L.,Tzeng Ovid,J.L.,&Wu,D.H.(2008).Flexible spatial mapping of different notations of numbers in Chinese readers.

Cognition,106

,1441?1450.Kadosh,R.C.(2008).Numerical representation:Abstract or nonabstract?.

The Quarterly Journal of Experimental Psychology,61

(8),1160?1168.Kadosh,R.C.,Henik,A.,&Rubinsten,O.(2008).Are Arabic and verbal numbers processed in different ways?.

Journal of Experimental Psychology:Learning Memory,and Cognition,34

(6),1377?1391.Korvorst,M.,&Damian,M.F.(2008).The differential influence of decades and units on multidigit number comparison.

The Quarterly Journal of Experimental Psychology,61

,1250?1264.Lindemann,O.,Abola fi a,J.M.,Pratt,J.,&Bekkering,H.(2008).Coding strategies in number space:Memory requirements in fl uence spatial-numerical associations.

The Quarterly Journal of Experimental Psychology,61

(4),515?524.Liu,C.,Mai,X.Q.,&Fu,X.L.(2004).The spatial numerical association of response codes effect of number processing in different attention conditions.

Acta Psychologica Sinica,36

(6),671?680.[劉超,買曉琴,傅小蘭.(2004).不同注意條件下的空間——數字反應編碼聯合效應.

心理學報,36

(6),671?680.]Mapelli,D.,Rusconi,E.,&Umiltà,C.(2003).The SNARC effect:An instance of the Simon effect?

Cognition,88

,B1?B10.Moyer,R.S.,&Landauer,T.K.(1967).Time required for judgments of numerical inequality

.Nature,215

,1519?1520.Nuerk,H.C.,Weger,U.,&Willmes,K.(2001).Decade breaks in the mental number line? Putting the tens and units back in different bins.

Cognition,82

,B25?B33.Nuerk,H.C.,Bauer,F.,Krummenacher,J.,Heller,D.,&Willmes,K.(2005).The power of the mental number line:How the magnitude of unattended numbers affects performance in an Eriksen task.

Psychology Science,47

(1),34?50.Nuerk,H.C.,Wood,G.,&Willmes,K.(2005).The universal SNARC effect.

Experimental Psychology,52

(3),187?194.Poltrock,S.E.,&Schwartz,D.R.(1984).Comparative judgments of multidigit numbers.

Journal of Experimental Psychology:Learning,Memory,and Cognition,10

,32?45.Schwarz,W.,&Keus,I.M.(2004).Moving the eyes along the mental number line:Comparing SNARC effects with saccadic and manual responses.

Perception &Psychophysics,66

(4),651?664.Shaki,S.,&Fischer,M.H.(2008).Reading space into numbers - A cross-linguistic comparison of the SNARC effect.

Cognition,108

(2),590?599.Shaki,S.,&Petrusic,W.M.(2005).On the mental representation of negative numbers:Context-dependent SNARC effects with comparative judgments.

Psychonomic Bulletin &Review,12

,931?937.Siegler,R.S.,Thompson,C.A.,&Schneider,M.(2011).An integrated theory of whole number and fractions development.

Cognitive Psychology,62

,273?296.Tzelgov,J.,&Ganor-Stern,D.(2004).Automaticity in processing ordinal information.In J.I.D.Campbell (Ed.),

Handbook of mathematical cognition

(pp.55?66).New York:Psychology Press.Varma,S.,&Schwartz,D.L.(2011).The mental representation of integers:An abstract-to-concrete shift in the understanding of mathematical concepts.

Cognition,121

,363?385.Varma,S.,&Karl,S.R.(2013).understanding decimal proportions:Discrete representations,parallel access,and privileged processing of zero.

Cognitive Psychology,66

,283?301.Wood,G.,Mahr,M.,&Nuerk,H.-C.(2005).Deconstructing and reconstructing the base-10 structure of Arabic numbers.

Psychology Science,47

,84?95.Zhang,Y.,&You,X.Q.(2012).Spatial representation of negative numbers induces spatial shifts of attention.

Acta Psychologica Sinica,44

(3),285?294.[張宇,游旭群.(2012).負數的空間表征引起的空間注意轉移.

心理學報,44

(3),285?294.]