船用大側斜螺旋槳的噪聲計算與分析

楊 光，房 毅，馮鵬飛

(中國人民解放軍91439部隊，遼寧 大連 116041)

0 引 言

螺旋槳噪聲是船舶的主要噪聲源之一，隨著螺旋槳設計方法的不斷改進，空泡起始航速較以往有所提高，無空泡噪聲問題凸現出來。而艦船的噪聲性能要求在不斷提高，研究螺旋槳無空泡噪聲越來越具有現實意義。螺旋槳噪聲的主要成分是負載噪聲[1]，而負載噪聲受螺旋槳軸承力影響很大[2]，其分析方法主要分為試驗測量和理論計算2種[3–4]，理論計算方法中一般先采用面元法或計算流體力學方法得到螺旋槳的脈動壓力，然后基于FW-H方程求解螺旋槳的負載噪聲[5–6]。

本文通過數值方法計算螺旋槳的無空泡噪聲，采用Virtual. Lab聲學計算軟件，根據聲類比理論和直接邊界元方法，分析伴流場中螺旋槳的無空泡噪聲規律，總結噪聲的衰減性、指向性等特性，還探究了螺旋槳軸承力與其噪聲特性之間的關系。

1 計算方法

1.1 流體計算模型

本文以材料為銅合金的5葉大側斜螺旋槳為研究對象，螺旋槳直徑為0.24 m，P/D0.7R=1.335，盤面比為0.72。在ICEM中建立計算流體力學模型，根據螺旋槳幾何參數通過Matlab編程得到各半徑處槳葉剖面的三維坐標點，通過點-線-面的建模順序建立螺旋槳模型[7]，如圖1所示。流體計算域分為旋轉域和靜止域，均劃分結構化網格，可以較為準確地控制槳葉邊界層和近壁面加密區域的網格尺寸。首先進行旋轉域單通道網格的創建（見圖2），在槳葉表面創建外O-Block，可以很好地解決槳葉周圍Block頂點處網格扭曲的問題。在葉根、導邊和隨邊處進行局部加密，螺旋槳周圍第1層網格尺寸為0.18 mm，然后旋轉單通道得到旋轉域整體網格。靜止域半徑為1.2 m，速度進口位于盤面前1.2 m處，壓力出口位于盤面后2 m處。將靜止域和旋轉域合并得到流體計算域網格，如圖3所示，最終網格數為400萬，網格質量為0.35以上。

圖 1 螺旋槳模型Fig. 1 Propeller model

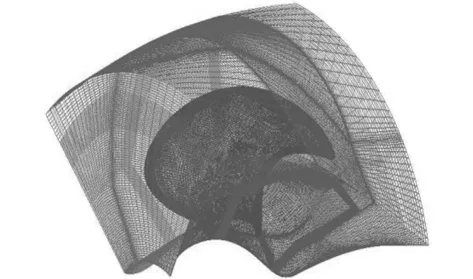
圖 2 旋轉域單通道網格Fig. 2 Rotating domain structured mesh

圖 3 流體計算域網格Fig. 3 Computation domain structured mesh

噪聲數值計算中選用分離渦模型（DES），是Spalart提出的一種結合經典雷諾時均（RANS）方程和大渦模擬（LES）湍流模型的混合方法，意在改善流動分離較為劇烈區域湍流模型的預報能力。DES采用RANS方法求解邊界層，在流動分離區域轉換成LES湍流模型，優先地從RANS模型預報分離流線，然后通過解決變化的湍流結構來捕捉非定常的動態分離剪切層，相比于LES方法可以顯著地節省計算資源[8]。

1.2 聲學計算模型

本文基于Lighthill聲類比理論[9]和FW-H方程[10]，對螺旋槳非均勻流場噪聲進行計算。Lighthill方程可以實現單獨計算聲源流場和聲場，如式（1）所示：

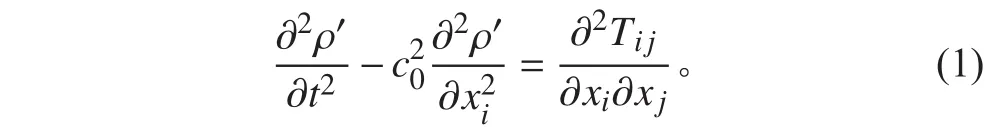
其中，Tij為Lighthill應力張量：

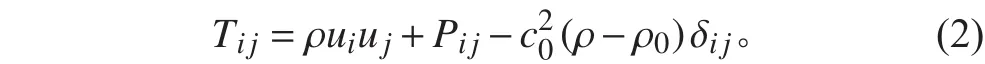
其中：σij為雷諾應力張量的粘性部分；Pij為可壓縮應力張量：

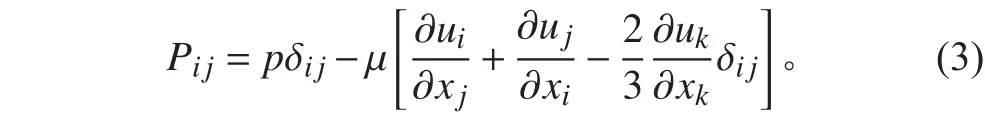
Curle將Lighthill理論推廣到考慮靜止固體邊界的影響。Ffowcs Williams和Hawkings進一步考慮了運動壁面的影響，得到FW-H方程：

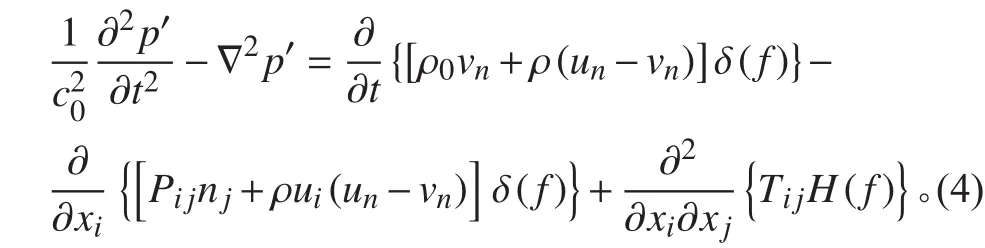
其中：c0為聲速；p'為壁面聲壓脈動；ui為流體速度在i方向的分量；vn為槳葉表面法向速度；un為槳葉表面流體法向速度分量；δ (f)為Dirac-δ函數；H (f)為Heaviside函數。等式右端分別為單極子、偶極子、四極子項。f=0表示輻射聲源表面，f＞0表示外部流場區域，f＜0表示聲源區。

與CFD流體計算網格不同，聲學網格尺寸L要滿足式（5）的要求。因此每個聲學網格的尺寸要小于0.25 m，在ICEM CFD中建立聲學網格，網格數為16 774，如圖4所示。

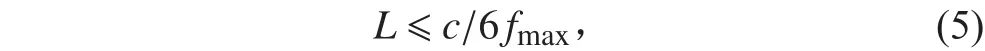
其中，水中聲速c=1 500 m/s；fmax為計算的最高頻率，

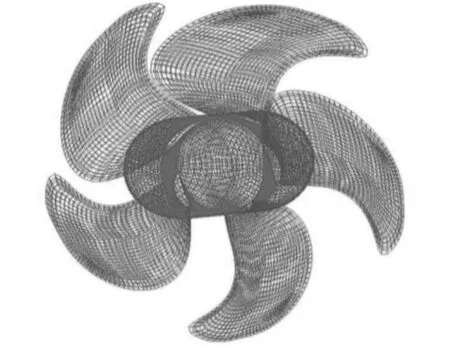
圖 4 聲學網格Fig. 4 Acoustic mesh

首先通過CFD方法求解伴流場中螺旋槳槳葉表面的時域軸承力，將螺旋槳葉面的壓力脈動作為旋轉偶極子聲源保存在CGNS文件中，將時域結果導入聲學計算軟件Virtual. Lab中，映射至聲學網格上并進行傅里葉變換，采用直接邊界元法計算螺旋槳的無空泡噪聲。計算流程如圖5所示。

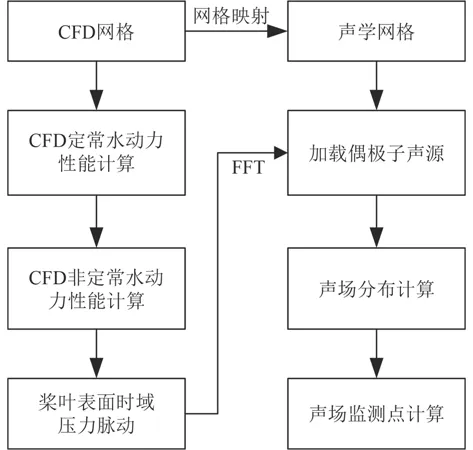
圖 5 螺旋槳噪聲計算流程Fig. 5 Flow chart of propeller noise prediction

2 螺旋槳軸承力和噪聲分析

2.1 軸承力計算及分析

采用CFX軟件計算螺旋槳槳葉表面的時域壓力脈動，伴流場是由在空泡水洞中采用假體模擬的方法測得的，得到槳盤面0.408，0.525，0.650，0.792，0.950，1.125半徑處每隔10°的軸向伴流分數。螺旋槳盤面處伴流場的軸向速度云圖如圖6所示。

圖 6 盤面處伴流場軸向速度云圖Fig. 6 Axial velocity contour of nominal wake field at paddle disk

本文時間步長Δt=0.000 5 s，即螺旋槳旋轉約2.3°記錄一次槳葉壓力脈動信息。求解模式選擇2階向后歐拉模式，靜止域和旋轉域的交界面類型為瞬態轉子-定子模型（Transient Rotor-Stator），數據傳遞選用GGI方式，用以計算滑動交界面處瞬態相互影響。

在進行非定常計算前，為了提高計算效率和精度，首先對其進行定常求解，待計算收斂后將其作為非定常計算的初始值，定常計算湍流模型選擇k-ω SST，在計算時將伴流場加載到流體計算模型的速度入口，選擇Inlet邊界條件；速度出口選擇Outlet邊界條件，相對壓力設為0 Pa；旋轉域與靜止域的交界面類型選擇凍結轉子交界面（Frozen Rotor）；其他壁面均選用無滑移壁面。

計算收斂后，槳葉自t=1.432 s時刻起每旋轉約90°吸力面和壓力面的壓力云圖如圖7和圖8所示。

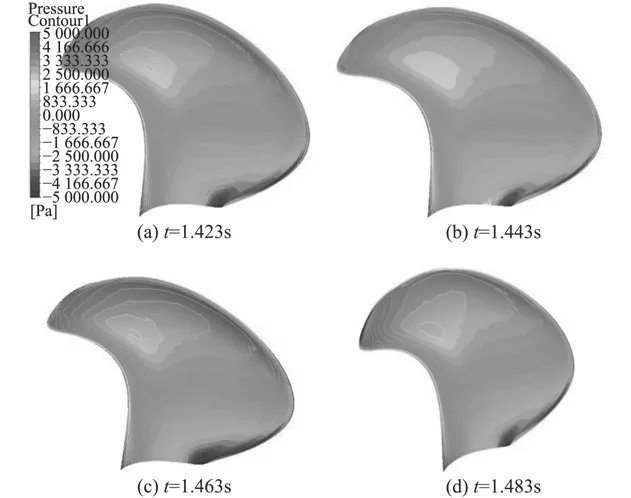
圖 7 壓力面壓力云圖Fig. 7 Pressure contours of pressure blade

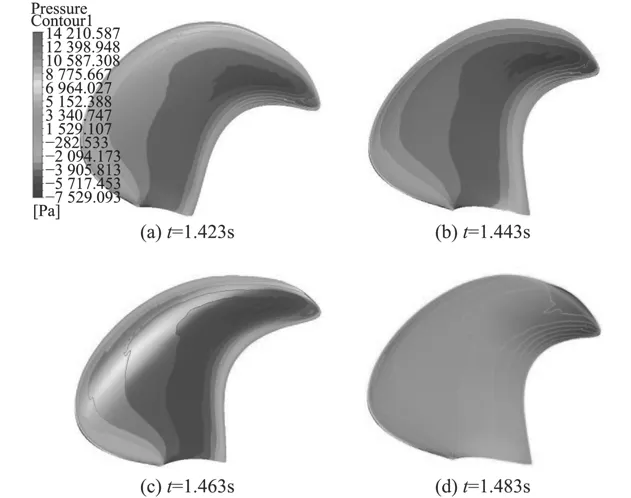
圖 8 吸力面壓力云圖Fig. 8 Pressure contours of suction blade

通過傅里葉變換將單槳葉和5個槳葉的時域軸承力轉換為頻域軸承力脈動信息，如圖9和圖10所示。單槳葉軸向脈動壓力幅值出現在軸頻和倍軸頻附近處，5個槳葉軸向脈動壓力幅值出現在葉頻和倍葉頻附近。其中葉頻（BPF）如式（6）所示，軸頻（PSF）

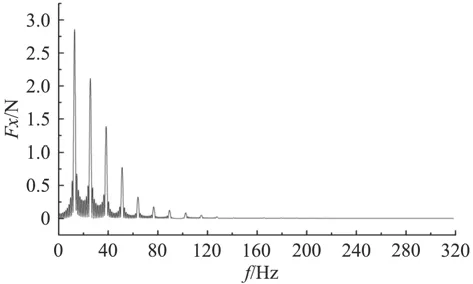
圖 9 單槳葉頻域內軸承力Fig. 9 Bearing force of single blade in frequency domain

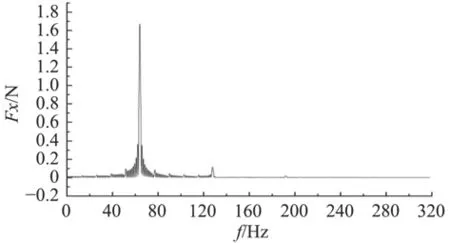
圖 10 五個槳葉頻域內軸承力Fig. 10 Bearing force of propeller in frequency domain

如式（7）所示：

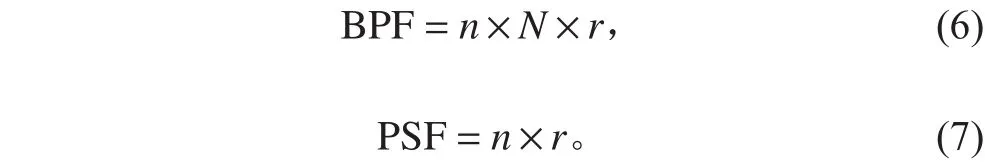
其中：n為葉頻、軸頻倍數；r為螺旋槳轉速，r=762 r/min；N為螺旋槳葉數，N=5。

2.2 噪聲計算及分析

建立聲場和聲壓監測點，如圖11所示。以螺旋槳為中心建立半徑為5 m的球形聲場，在x，y，z軸距離槳盤面圓心1，2，3倍直徑處建立聲壓監測點，分別命名為X1，X2，X3；y，z軸監測點命名方式與x軸布置相同。為了研究螺旋槳噪聲指向性，分別在槳盤面和垂直于槳盤面的平面上，以槳軸心為圓心，每隔15°布置1個噪聲監測點。

圖 11 聲場監測點Fig. 11 Monitor points of acoustic field

通過計算得到x軸和y軸監測點的噪聲頻譜曲線，如圖12～圖13所示，z軸監測點的噪聲頻譜曲線與y軸相似。根據式（8）可得各監測點的總聲壓級，如表1所示。Virtual. Lab軟件中參考聲壓為空氣中的參考聲壓（2×10–5Pa），為了轉換為水中的參考聲壓（1×10–6Pa），需要在計算得到的各監測點總聲壓級上直接加26 dB。

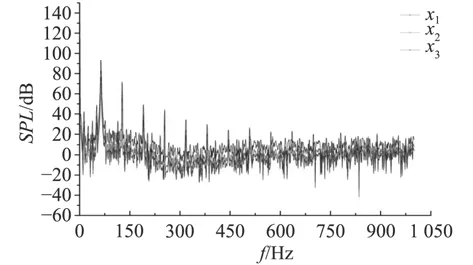
圖 12 x軸監測點噪聲頻譜曲線Fig. 12 The acoustic spectrum curves at x direction monitor points

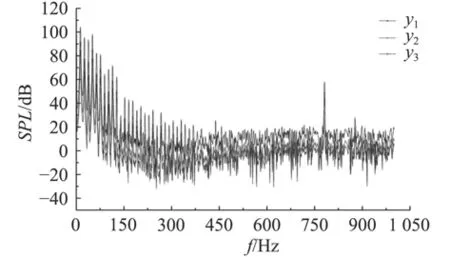
圖 13 y軸監測點噪聲頻譜曲線Fig. 13 The acoustic spectrum curves at y direction monitor points

表 1 監測點總聲壓級Tab. 1 Total spl on acoustic monitor points

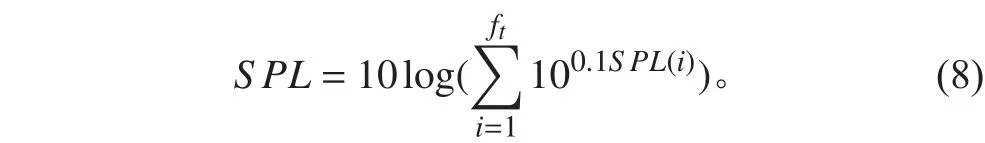
由各監測點總聲壓級可知，聲強隨著距螺旋槳距離的增加而減小，在距離槳盤面圓心相同距離處軸向總噪聲級最小。從x軸各點噪聲頻譜特性可得，在螺旋槳1階葉頻和倍葉頻附近聲壓級出現幅值，從y軸、z軸各點噪聲頻譜特性可得，在螺旋槳1階軸頻和倍軸頻附近聲壓級出現幅值。單槳葉軸向脈動壓力幅值出現在軸頻和倍軸頻附近處（見圖9），和y軸、z軸噪聲頻譜曲線規律一致；5個槳葉軸向脈動壓力幅值出現在葉頻和倍葉頻附近（見圖10），和x軸噪聲頻譜曲線規律一致，此規律也驗證了數值計算方法的準確性，而且1階葉頻處槳葉脈動壓力對總聲壓級影響最大。

螺旋槳盤面處的噪聲指向性圖（見圖14）表明，槳盤面上相同監測點處的聲壓隨葉頻階次的增加而減小，這是由于軸承力脈動幅值隨著葉頻階次的增加而減小；槳盤面處1階、2階、3階葉頻各監測點處的聲壓級相差不大，噪聲指向性基本呈圓形；1階葉頻處的噪聲云圖關于軸心對稱性較好，說明1階葉頻處的噪聲指向性受伴流場不均勻性影響較小，而2階、3階葉頻處的云圖對稱性較差，說明2階、3階葉頻處的噪聲指向性受伴流場不均勻性影響較大。

螺旋槳軸向縱剖面處的噪聲指向性圖（見圖15）表明，軸向縱剖面聲壓級最小值均出現在螺旋槳正上方和正下方，聲壓級最大值出現在軸向上，軸向縱剖面噪聲指向性均呈水平“8”字形，1階葉頻噪聲指向性“8”字基本關于盤面對稱，說明螺旋槳上下游的聲壓級相近，2階和3階葉頻處螺旋槳下游各點聲壓級明顯高于上游。

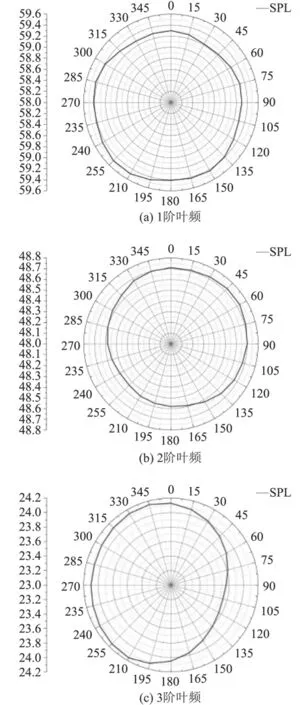
圖 14 槳盤面噪聲指向性Fig. 14 Noise directivity of paddle disk

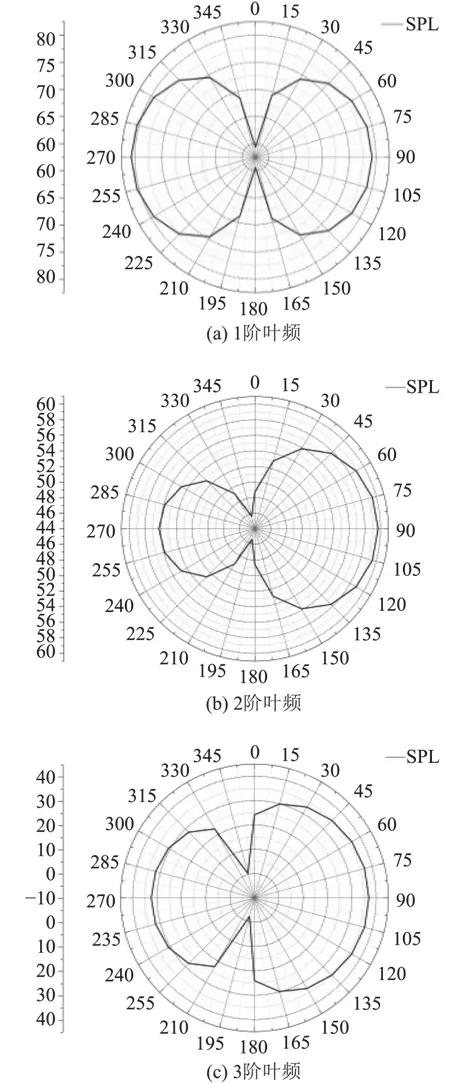
圖 15 軸向縱剖面噪聲指向性Fig. 15 Noise directivity of the axial longitudinal section

3 結 語

本文首先針對大側斜螺旋槳，采用DES方法對伴流場中螺旋槳的軸承力進行數值計算，得到軸承力的時域值，通過傅里葉變換得到頻域脈動值并分析了軸承力的頻域特性；將槳葉表面壓力脈動作為旋轉偶極子聲源，采用Virtual. Lab計算了螺旋槳的無空泡噪聲，分析了螺旋槳軸承力與噪聲的關系以及噪聲指向性。得到如下結論：

1）單槳葉軸向脈動壓力幅值出現在軸頻和倍軸頻附近處，5個槳葉軸向脈動壓力幅值出現在葉頻和倍葉頻附近。

2）聲壓隨著距離的增加而減小，在距離槳盤面圓心相同距離處軸向總噪聲級最小。y軸，z軸噪聲幅值出現在軸頻和倍軸頻附近處，與單槳葉軸向脈動壓力規律一致；x軸噪聲幅值出現在葉頻和倍葉頻附近，與5個槳葉軸向脈動壓力規律一致。1階葉頻處槳葉脈動壓力對總聲壓級影響最大。

3）螺旋槳一階葉頻處，槳盤面的噪聲指向性受伴流場的不均勻性影響較小，軸向縱剖面的噪聲指向性上下游對稱；2階和3階葉頻處，槳盤面的噪聲指向性受伴流場的不均勻性影響較大，軸向縱剖面的噪聲指向性下游聲壓大于上游。

[1]SEOL H, SUH J, LEE S. Development of hybrid method for the prediction of underwater propeller noise[J]. Journal of Sound and Vibration, 2005, 288(1–2): 345–360.

[2]蘇玉民, 竇鳳祥, 劉業寶, 等. 螺旋槳無空泡噪聲的研究[J].武漢理工大學學報: 交通科學與工程版, 2013, 37(5):895–899.

Su Yu-min, DOU Feng-xiang, LIU Ye-bao, et al. Study of noncavitating propeller noise[J]. Journal of Wuhan University of Technology (Transportation Science &Engineening), 2013,37(5): 895–899.

[3]王超, 黃勝. 螺旋槳噪聲預報方法的綜述[C]//黑龍江省造船工程學會2008年學術年會論文集, 2008.

[4]趙小龍, 熊鷹. 預報螺旋槳噪聲的方法[J]. 艦船科學技術,2005, 27(2): 42–45.

ZHAO Xiao-long, XIONG Ying. The method of predicting propeller noise[J]. Ship Science and Technology, 2005, 27(2):42–45.

[5]謝劍波, 周其斗. 非均勻流場中螺旋槳線譜噪聲指向性分析[J]. 中國艦船研究, 2010, 5(6): 6–11.

XIE Jian-bo, ZHOU Qi-dou. Directivity prediction on tone noise of propeller operating in non-uniform flows[J]. Chinese Journal of Ship Research, 2010, 5(6): 6–11.

[6]KATO C. Applications of fully-resolved large eddy simulation to unsteady fluid flow and aeroacoustic preditions[C]//International Symposium on Turbulence and Shear Flow Phenomena, TSFP-7, Ottawa, Canada.

[7]黃璐, 陳立. 螺旋槳建模方法及敞水性能研究[J]. 艦船電子工程, 2014, 34(8): 78–88.

HUANG Lu, CHEN Li. Research on modeling method of propeller[J]. Ship Electronic Engineering, 2014, 34(8): 78–88.

[8]王超. 螺旋槳水動力性能、空泡及噪聲性能的數值預報研究[D]. 哈爾濱: 哈爾濱工程大學, 2010.

[9]LIGHTHILL M J. On sound generated aerodynamically.PartⅠ.General theory[M].Proc.R. Soc. London Ser. A 211:564–587.

[10]FFOWCS WILLIAMS J E, HAWKINGS D L. Sound generation by turbulence and surfaces in arbitrary motion.[J].Philosophical Transactions of the Royal Society A Mathematical Physical and sengineering Sciences, 1969,264(1151):321–342.