氣井攜液機理與臨界參數研究

耿 新 中

中國石化中原油田分公司天然氣產銷廠

1 攜液工況診斷方法簡介

1.1 臨界流速法

臨界流速法認為，氣流流速決定了氣流的攜液能力，連續攜液時，液滴是液相存在的主要形式，霧流是基本流型。假設液滴為圓球形，依據質點力學理論，如果上升氣流對液滴施加的拖曳力等于液滴的重量，液滴將以滯止狀態懸浮于氣流中，此時的氣流流速即為氣流攜帶液滴上行所需要的最小流速——攜液臨界流速，可以用下式表示[11]：

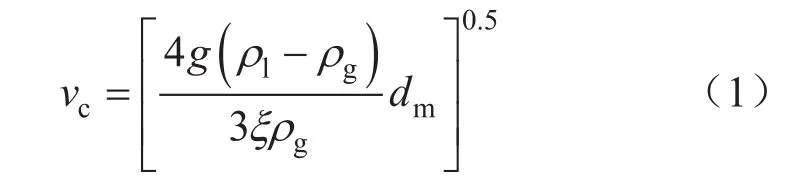
式中vc表示攜液臨界流速，m/s；g表示重力加速度,9.81 m/s2；ρl表示液體密度，kg/m3；ρg表示氣體密度，kg/m3；ξ表示無因次曳力系數；dm表示液滴直徑，m。

除了重力和浮力外，懸浮液滴還要受到兩種力的影響：一種是由氣流的沖擊作用形成的使液滴趨于變形破壞的速度壓力一種是由界面張力形成的使液滴趨于保持完整性和圓球形的表面壓力（σ/dm）。兩種壓力對抗的結果，決定了氣流中最大液滴的形狀和大小。如果液滴是圓球形，則最大液滴的直徑與氣流流速之間存在如下關系[11]：

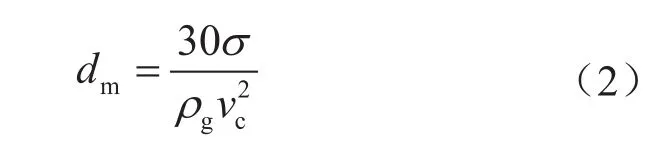
式中σ表示界面張力系數，N/m；

將式（2）代入式（1），可得到攜液臨界流速法模型的通用表達式：

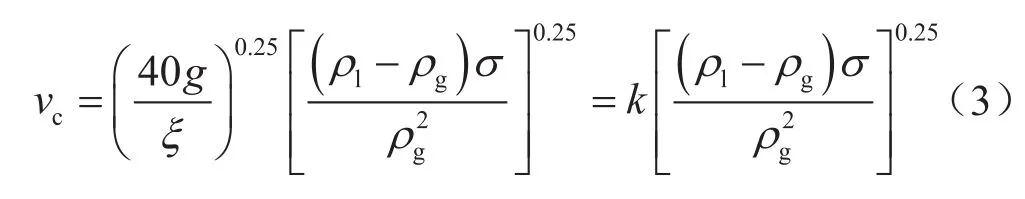
式中k表示模型系數。

進而得到考慮截面持液率影響的攜液臨界產氣量計算式為：

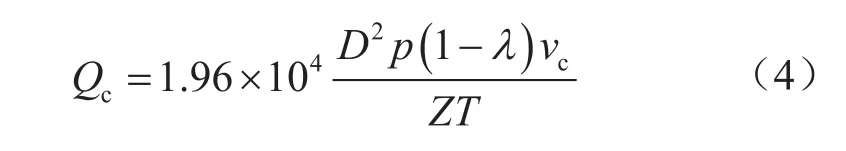
式中Qc表示攜液臨界產氣量，104m3/d；D表示圓管直徑，m；p表示壓力，MPa；λ表示截面持液率；Z表示氣體偏差因子；T表示溫度，K。

由式（3）可知，液滴的形狀不同，則無因次曳力系數取值不同，導致模型系數不同（表1），進而造成攜液臨界流速的大小也不同。因此，基于對液滴形狀認識的不同，學者們研究并提出了很多不同的臨界流速法模型，由于模型系數的不同，導致攜液臨界流速的計算結果差別很大。常見的模型如表1中的模型Ⅰ—Ⅵ。

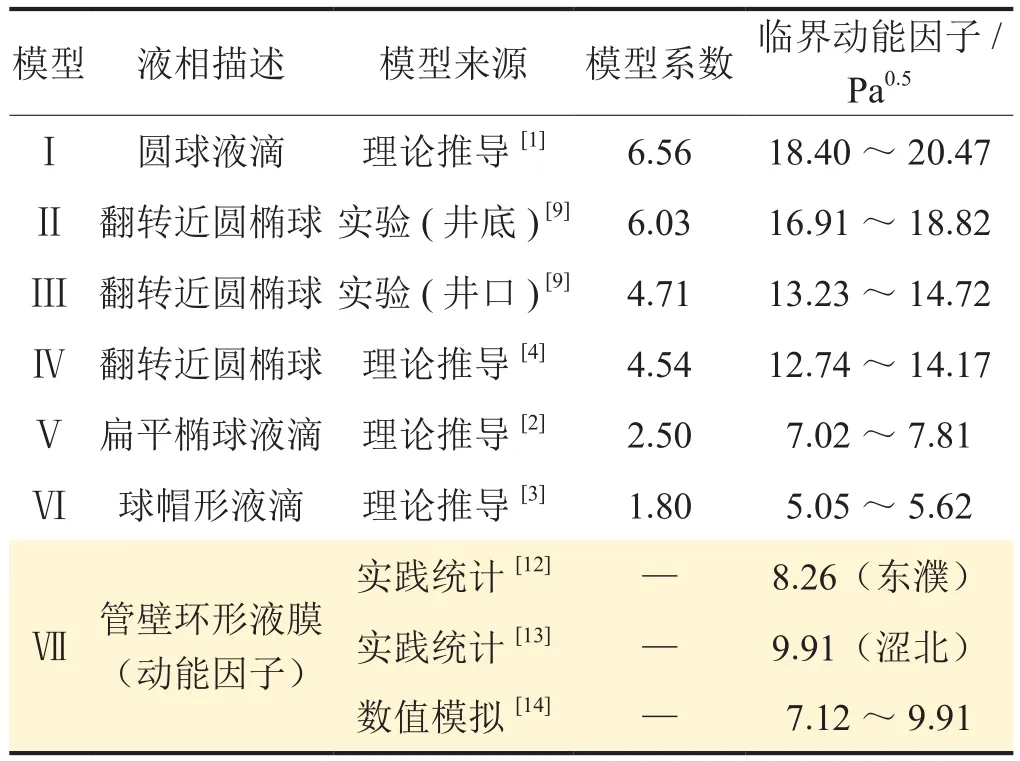
表1 常見氣流攜液臨界工況診斷模型與參數表

1.2 臨界動能因子法

臨界動能因子法認為，氣流的動能因子決定了氣流的攜液能力，動能因子的大小與氣流的流速和密度有關[11-12]。受管流截面中液相占比不易確定的影響，氣流的實際流速很難準確求取，實際應用中，一般用更容易獲取的不考慮液相影響的表觀參數來代替，即

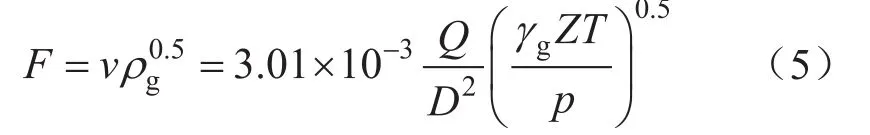
式中F表示動能因子，Pa0.5；v表示流速，m/s；Q表示產氣量，104m3/d；γg表示氣體相對密度。

實踐表明，連續攜液的最小動能因子近似為常數，稱為臨界動能因子。用臨界動能因子代替動能因子，可以得到攜液臨界產氣量的表達式：

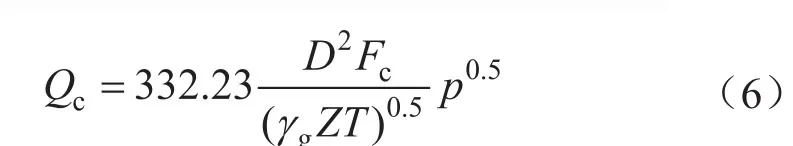
式中Fc表示臨界動能因子，Pa0.5。

依據區域性的實踐數據統計，本文參考文獻[12-13]分別把8.0和9.6作為臨界動能因子，用于連續攜液工況的判斷，取得了良好的效果。因本文參考文獻[12-13]中動能因子計算式的系數與式（5）略有差別，為保證本文參數對比的一致性，按式（5）計算，實踐數據統計臨界動能因子分別取值8.26 Pa0.5和9.91 Pa0.5（表 1）。

2 兩相垂管流氣流攜液形式探討

診斷方法和模型是否合理，取決于其與攜液機理是否符合。分析表明，目前廣泛應用的臨界流速法雖然得到了業界的普遍認同，但仍然存在很多疑點，突出表現在以下3個方面。

1）很多氣井實測的井筒流壓梯度很大，明顯與形成分散液滴和霧流流型所需的低液氣比條件不符合，但卻仍然能夠連續攜液生產，說明連續攜液的流型未必只是霧流，液相存在的形式也并非只有液滴。

2）根據式（4）可知，截面持液率越大，即液量越大，需要的攜液臨界產氣量反而會越小，這顯然不合常理。

3）根據可視化實驗條件[9]，取ρl=1 000 kg/m3，σ=0.076 N/m，將實驗模型Ⅱ代入式（2），計算得出的液滴直徑約為7.19 mm，計算過程如下：

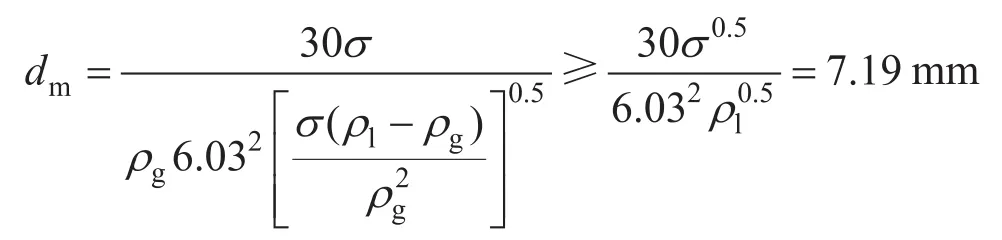
而實驗條件提供的人工霧化液滴直徑只有0.15 mm，前者是后者的近48倍。如果分散液滴確實是液相存在的主要形式，由實驗數據統計，根本就不可能得到模型Ⅱ。反之，模型Ⅱ依據的實驗數據，證明了分散液滴肯定不是連續攜液時液相存在的主要形式。

以上疑點說明，以懸浮液滴和霧流流型為基礎的臨界流速法并不合理。

2.1 兩相垂管流基本特征與氣流攜液形式分析

根據流體力學基本理論，圓管流動的基本特征是管流橫截面上流速存在徑向差異[15]，即管流中心軸線處的流速最高，沿徑向流速逐漸降低，如圖1所示，流速沿徑向變化的表達式為：

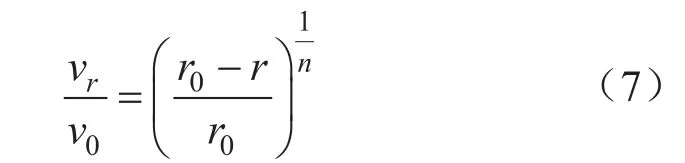
式中vr表示距軸線r處的流速，m/s；v0表示軸線處的流速，m/s；r表示距軸線的距離，m；r0表示圓管半徑，m；n表示隨雷諾數變化的指數。

1）受速度壓力和上下壓差的共同影響，規則的圓球形狀將無法保持，液滴勢必會產生變形。

2）液滴表面橫向對稱點受到的切向拖曵力分量的差異，會對液滴施加一個切向旋轉合力，使液滴產生旋轉。受旋轉離心效應的影響，變形液滴的靜態理論形狀[2-8]根本無法保持，其動態形狀必然趨近于圓橢球。這就是實驗觀察到的液滴是持續旋轉的近圓橢球而非其他形狀的原因[9]。

3）液滴表面橫向對稱點受到的徑向推力分量的差異，會對液滴施加一個偏向推動合力，使得液滴運移的總趨勢將不會是直上直下，在向上運移的同時，總是會趨于向管壁方向偏移，最終抵達并附著于管壁形成環膜，懸浮液滴攜液形式失去基礎，基于懸浮液滴和霧流流型的臨界流速法，實際上無從談起。

2.2 兩相垂管流氣流攜液的形式探討

在兩相垂管流中，如果液相不能被連續攜帶，將會逐漸形成積液，其表現必然是氣相的不連續；反之，如果能夠保持氣相的連續性，則不論液相是什么存在形式[16]，都必定處于被連續攜帶的狀態。

根據兩相垂管流流型劃分，連續氣相在過渡流形成，在環霧流時趨于穩定。本文參考文獻[17]指出，只要截面持液率不大于24%，就可以保持氣相的連續性。如此大的持液率，液相顯然不會僅僅是懸浮液滴，流型也顯然不會是霧流，而只能是環霧流或接近環霧流的過渡流。

在環霧流中，液相以管壁環膜和中心氣流中的液滴兩種形式存在[9,14]，氣流攜液呈現如下特征（圖1）。

在連續氣相條件下，管壁環膜被中心氣流連續攜帶上行。同時受氣流的拖曳影響，氣液界面處會不斷分離出液滴進入中心氣流[14]。

由于管流橫截面上流速存在徑向差異的影響，中心氣流中的液滴總是會產生偏向移動匯入管壁環膜。因此，管壁環膜將成為氣流連續攜液時液相存在的主要形式，而不是分散的液滴。這就是實驗數據統計得到的臨界流速法模型Ⅱ和模型Ⅲ與實驗的前提條件不一致的原因[9]。

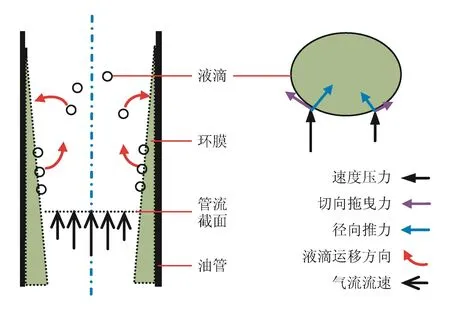
圖1 兩相垂管流氣流攜液及液滴受力示意圖

氣流拖曳力的強弱決定了液滴分離的數量并影響氣流中液滴的濃度；液滴的濃度又決定了氣流中液滴匯入管壁環膜的數量。當氣流拖曳力增強，液滴分離數量大于匯入環膜數量時，環膜漸薄；反之，環膜漸厚。伴隨氣流拖曳力的變化，逐步形成管壁環膜與氣流之間液滴交換的動態平衡。

當氣流拖曳力足夠強，管壁環膜的液滴分離數量總是大于匯入數量時，環膜逐漸消失，最后呈現為完全的霧流。因此，霧流只是環霧流的一個零液膜特例。在可視化實驗[9]中，觀察井口連續攜液時，明顯存在液相環膜，本身就證明了環膜流攜液形式的客觀存在。為了觀察井底積液，需要更高的氣流流速以清除管壁液膜，這就是實驗得到的模型Ⅱ（零液膜）要比模型Ⅲ（有液膜）的攜液臨界流速大的原因。

綜上所述，兩相垂管流積液的原因不是懸浮液滴不能被攜帶，而是氣相無法保持連續。氣流連續攜液時液相存在的主要形式是管壁環膜，管流的基本流型是環霧流。臨界流速法忽視了橫截面上流速存在徑向差異這一管流基本特征，錯把有限截面的管流當成橫截面上流速無差異的無限大空間層流去研究，適用場景與積液定義錯誤，不符合兩相垂管流條件下氣流攜液的實際，是一個認識誤區。

3 臨界動能因子法的適應性分析

由上文可知，臨界流速法不適用于管流攜液工況的診斷。對于臨界動能因子法，本文參考文獻[12-13]雖然給出了連續攜液臨界動能因子的實踐統計值，但并未對動能因子的物理意義和理論可靠性進行討論，因而沒有得到業界廣泛的認同，對于其適應性，有必要開展進一步的研究。

3.1 臨界動能因子的物理意義

氣體密度公式為：

式中Mg表示氣體質量，kg；Vg表示氣體體積，m3。

將式（8）代入式（5），并對動能因子和臨界動能因子表達式進行變換，推導可得：

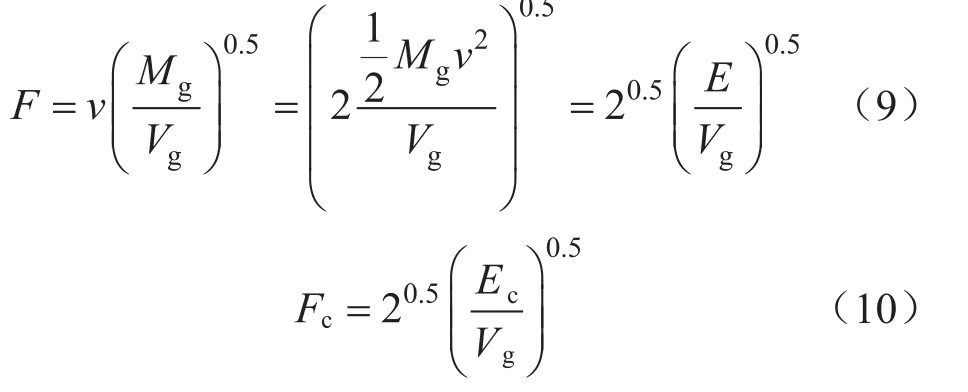
式中E表示動能，J；Ec表示臨界動能，J。

可見，動能因子是單位體積氣流所具有的動能的函數。臨界動能因子的物理意義是：滿足連續攜液工況時單位體積氣流所需具有的最小動能即臨界動能。

3.2 動能因子與圓管流動能量損耗

根據能量守恒定律，氣體圓管流動的能量方程如下[11]：

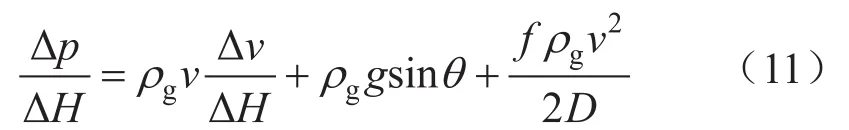
式（11）中，動能變化項、勢能變化項反映了氣相自身流動物性參數變化所損耗的能量，摩阻損失項則反映了氣相克服管壁摩阻等其他因素所損耗的能量，與摩阻系數（f）有關。對比式（5），摩阻損失項可變換為：

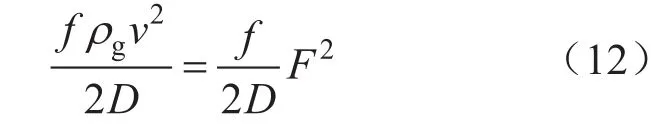
在連續攜液的環霧流工況下，如果把管壁環膜的內表面看作是氣流單相流動的邊界，摩阻損失項就反映了氣流克服環膜自重與管壁間的流動摩阻，并賦予環膜連續向上流動的動能所損耗的能量，與動能因子的平方成正比。用氣液兩相之間的摩阻系數（fgl）、臨界流速（vc）、臨界動能因子（Fc）分別替代f、v、F后，可得：

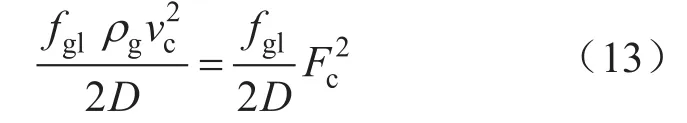
式中fgl表示氣液兩相之間的摩阻系數。

由式（13）可見，臨界動能因子的平方與氣流攜帶液體環膜上行最小需要損耗的能量成正比，反映了氣流連續攜液所需要損耗的能量的大小，攜液機理更符合能量守恒定律。

3.3 動能因子與兩相流型

根據式（9）、（10）、（12）看出，動能因子代表了氣流攜液能力的大小。流型為環霧流時，隨動能因子增大，氣流拖曳力增強，液滴自環膜分離的數量大于匯入數量，環膜漸薄，直至形成零環膜的霧流流型；反之，環膜漸厚，直至形成氣液兩相均不連續的段塞流流型。管流攜液工況變化的本質是動能因子（單位體積氣流所具有的動能）的量變引起的兩相流型的質變。

需要說明的是，當生產液氣比較高，管流中截面持液率恒大于24%時，將無法形成連續的氣相，管流中將總是呈現出氣液交互的段塞流特征，此時，動能因子再大，攜液也不連續。但因為動能因子足夠大，氣流攜液的能量充足，氣井未必會積液停產。這種現場經常出現的現象是臨界流速法無法解釋的，但用臨界動能因子法解釋，就是一種正常現象。

3.4 臨界動能因子法的適應性

由上文可知，在臨界動能因子的計算中，并未考慮截面持液率，只是一個表觀值。如果考慮截面持液率，對式（10）和式（6）分別進行變換，可分別得到中心氣流的實際臨界動能因子和實際臨界產氣量的計算式：

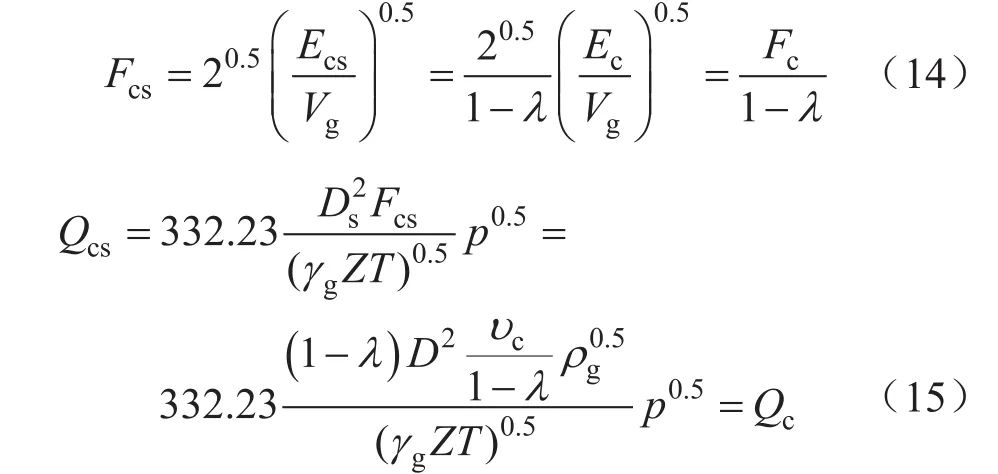
式中Fcs表示實際臨界動能因子，Pa0.5；Ecs表示實際臨界動能，J；Qcs表示實際臨界產氣量，104m3/d；Ds表示與λ對應的中心氣柱直徑，m。

由式（14）可知，臨界動能因子不變，截面持液率增大時，中心氣流的實際臨界動能因子也增大，單位體積氣流的實際臨界動能更是呈幾何級數增長，符合更多的液體需要更大的能量攜帶的常識。

由式（15）可知，不論截面持液率如何變化，用臨界動能因子計算出的攜液臨界產氣量均不變。對比臨界流速法攜液臨界產氣量計算式（4）得到的“截面持液率越大，即液量越大，需要的攜液臨界產氣量反而越小”的反常結論，臨界動能因子法顯然更合理。

綜上所述，臨界動能因子法直觀地體現了流體流動依賴于能量驅動的物理學基本原理，攜液機理符合能量守恒定律和管流特征，診斷參數具有自適應性，在攜液工況診斷方面，具有本質合理性。

下面，對個別臨界流速法模型進行攜液工況診斷的結果與現場實際也相符合的原因進行分析。

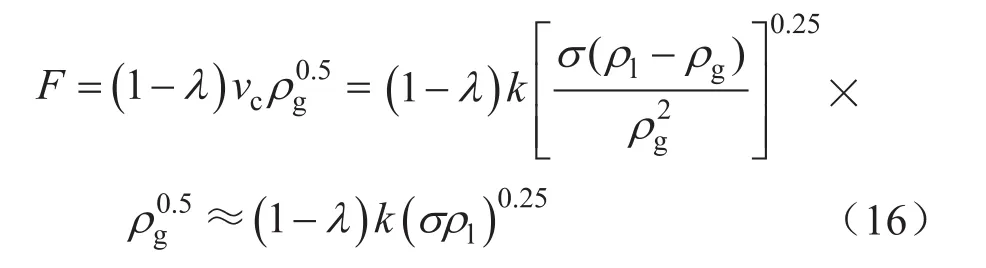
因為σ、ρl變化很小，變化更小。根據式（16），截面持液率很小時，每一個臨界流速法模型分別對應著一個臨界動能因子取值區間（表1），同一氣藏的σ、ρl近似不變，則動能因子近似為一個常數，如果這個動能因子恰好接近于連續攜液的臨界動能因子，兩相流動處于環霧流或接近于環霧流的過渡流流型，就不會產生明顯的積液，則表面上看這個模型就是與現場實際相符合的，但實際上卻僅僅是一個巧合。

4 臨界動能因子取值研究

對于臨界動能因子的數值，目前還沒有成熟的理論計算方法。現場實踐數據統計（表1）是一個有益的探索，但通用性依據不足。

本文參考文獻[14]用硅油＋空氣體系對填料表面液膜垂向流動特征開展的數值模擬研究表明，氣流的動能因子不同，液膜的流動特征不同。隨著動能因子增大，氣流攜液能力逐漸增強，液膜先后呈現出與兩相垂管流的氣泡流、段塞流、過渡流、環膜流、霧流等流型完全類似的流動特征。其中：動能因子為5.418 Pa0.5時，局部液膜整體向上流動，呈現過渡流特征；動能因子為6.772 Pa 時，全部液膜整體向上流動、并伴隨著液滴自液膜的分離與匯入，呈現環霧流特征。因此，硅油＋空氣體系環霧流的臨界動能因子應介于5.418 Pa0.5與6.772 Pa0.5之間。因為鹽水與硅油的σ與ρl不同，不同氣藏產出水的σ與ρl也會有所差異，按式（16）類比計算，鹽水＋天然氣體系的環霧流臨界動能因子應介于7.125 Pa0.5與9.907 Pa0.5之間（表2）。

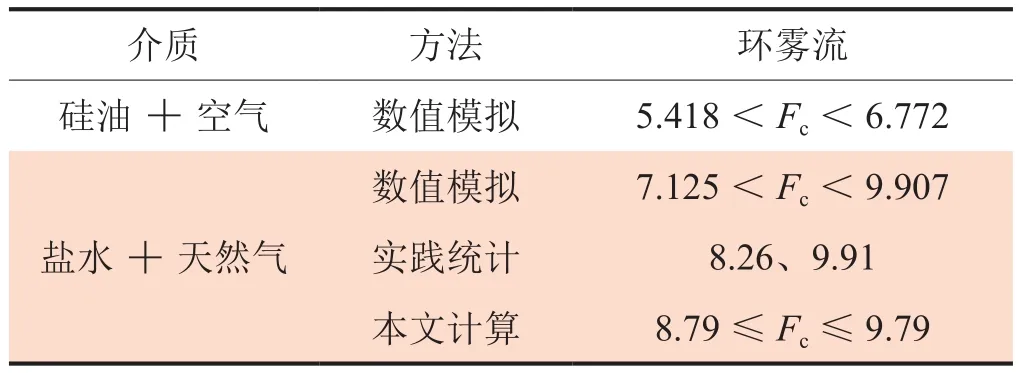
表2 臨界動能因子Fc對照表 Pa0.5

下面，依據本文提出的攜液機理，對連續攜液環霧流的臨界動能因子進行分析計算。

由式（9）、（10）可知，臨界動能因子必然對應著一個臨界流速，盡管這個流速不同于臨界流速法中的臨界流速，但作為環霧流的零液膜特例，滿足零液膜工況時的最小氣流流速卻可以看成是霧流的臨界流速。根據可視化實驗過程，為了觀察井底積液而完全清除管壁環膜得到的模型Ⅱ，攜液工況更符合霧流特征[9]。因為實驗液氣比極低，零液膜時λ很小，由式（16），模型Ⅱ可以近似簡化為：

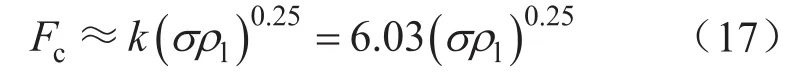
考慮不同氣藏σ與ρl的大小不同，霧流的臨界動能因子取值區間為16.91～18.82 Pa0.5，計算過程如下：

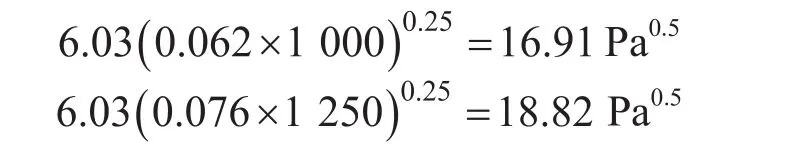
當截面持液率為24%時，假設中心氣流自身滿足霧流工況的臨界動能因子條件，則折算到整個管流截面的臨界動能因子取值區間為12.85～14.31 Pa0.5，計算過程如下：

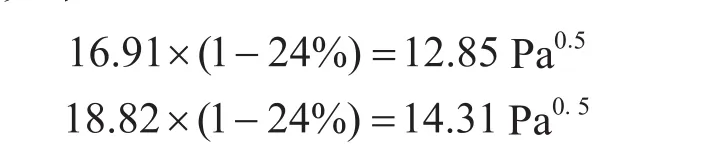
但是，因為霧流是環膜無法保持的工況條件，如果中心氣流保持霧流的臨界動能因子，環膜將會逐漸減少，趨于形成零環膜。因此，12.85～14.31 Pa 應該是一個保持動態平衡的中間值。則截面持液率為24%時，環霧流的臨界動能因子取值區間應為8.79～9.79 Pa0.5，計算過程如下：

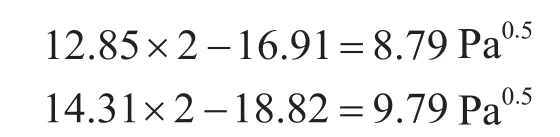
與表2數據對比，可以看出，按照本文提出的攜液機理，結合實驗模型分析[9]計算得到的臨界動能因子，與數值模擬[14]和實踐統計[12-13]得到的數值基本一致。證實了本文關于攜液機理與攜液形式分析的合理性。

綜上所述，動能因子越大，氣流攜液能力越強。同一氣藏的σ與ρl近似不變，連續攜液環霧流的臨界動能因子近似為常數；不同氣藏的σ與ρl不同，臨界動能因子雖不同但差別小，取值區間為8.79～9.79 Pa0.5，選取較大值近似取整為10 Pa0.5，對任意氣藏具有通用性。

5 結論與認識

1）兩相垂管流積液的原因不是懸浮液滴不能被攜帶，而是氣相無法保持連續。連續攜液的主要形式是管壁環膜流動，基本流型是環霧流。

2）氣流攜液的實質是能量驅動，兩相垂管流攜液工況變化的本質是單位體積氣流動能的量變引起的兩相流型的質變。

3）以動能因子為基礎的臨界動能因子法，直觀地體現了流體流動依賴于能量驅動的物理學基本原理，攜液機理符合兩相管流基本特征和能量守恒定律，具有本質合理性；以懸浮液滴和霧流流型為基礎的臨界流速法，忽視了橫截面上流速存在徑向差異這一管流基本特征，適用場景與積液定義錯誤，是一個認識誤區。

4）連續攜液臨界動能因子近似為常數，受液相物性影響，不同氣藏略有差別。綜合實驗分析、實踐統計和數值模擬結果，提出環霧流臨界動能因子的通用取值為10 Pa0.5。

[1] Turner RG, Hubbard MG & Dukler AE. Analysis and prediction of minimum ぼow rate for the continuous removal of liquids from gas wells[J]. JPT, 1969, 21(11): 1475-1482.

[2] 李閩, 郭平, 譚光天. 氣井攜液新觀點[J]. 石油勘探與開發,2001, 28(5): 105-106.Li Min, Guo Ping & Tan Guangtian. New look on removing liq-uids from gas wells[J]. Petroleum Exploration and Development,2001, 28(5): 105-106.

[3] 王毅忠, 劉慶文. 計算氣井最小攜液臨界流量的新方法[J]. 大慶石油地質與開發, 2007, 26(6): 82-85.Wang Yizhong & Liu Qingwen. A new method to calculate the minimum critical liquids carrying ぼow rate for gas wells[J]. Petroleum Geology & Oilベeld Development in Daqing, 2007, 26(6):82-85.

[4] 彭朝陽. 氣井攜液臨界流量研究[J]. 新疆石油地質, 2010,31(1): 72-74.Peng Chaoyang. Study on critical liquid-carrying flow rate for gas well[J]. Xinjiang Petroleum Geology, 2010, 31(1): 72-74.

[5] 何順利, 欒國華, 楊志, 公玉娟, 申穎浩, 郭雪晶. 一種預測低壓氣井積液的新模型[J]. 油氣井測試, 2010, 19(5): 9-13.He Shunli, Luan Guohua, Yang Zhi, Gong Yujuan, Shen Yinghao& Guo Xuejing. A new model for predicting liquid loading in low energy wells[J]. Well Testing, 2010, 19(5): 9-13.

[6] 熊健, 李凌峰, 張濤. 氣井臨界攜液流量的計算方法[J]. 天然氣與石油, 2011, 29(4): 54-56.Xiong Jian, Li Lingfeng & Zhang Tao. Calculation of critical liquid carrying ぼow rate in gas well[J]. Natural Gas and Oil, 2011,29(4): 54-56.

[7] 周德勝, 張偉鵬, 李建勛, 宋鵬舉. 氣井攜液多液滴模型研[J].水動力學研究與進展: A輯, 2014, 29(5): 572-579.Zhou Desheng, Zhang Weipeng, Li Jianxun & Song Pengju.Multi-droplet model of liquid unloading in natural gas wells[J]Chinese Journal of Hydrodynamics, 2014, 29(5): 572-579.

[8] 王自彬, 李穎川. 氣井連續攜液機理[J]. 石油學報, 2012,33(4): 681-686.Wang Zibin & Li Yingchuan. The mechanism of continuously removing liquids from gas wells[J]. Acta Petrolei Sinica, 2012,33(4): 681-686.

[9] 魏納, 李穎川, 李悅欽, 劉安琪, 廖開貴, 喻欣. 氣井積液可視化實驗[J]. 鉆采工藝, 2007, 30(5): 43-45.Wei Na, Li Yingchuang, Li Yueqin, Liu Anqi, Liao Kaigui & Yu Xin. Visual experimental research on gas well liquid loading[J].Drilling & Production Technology, 2007, 30(5): 43-45.

[10] 趙哲軍, 劉通, 徐劍, 朱江, 楊逸. 氣井穩定攜液之我見[J].天然氣工業, 2015, 35(6): 59-63.Zhao Zhejun, Liu Tong, Xu Jian, Zhu Jiang & Yang Yi. Stable fluid-carrying capacity of gas wells[J]. Natural Gas Industry,2015, 35(6): 59-63.

[11] 楊川東. 采氣工程[M]. 北京: 石油工業出版社, 1997: 48-141.Yang Chuandong. Natural gas production engineering[M]. Beijing: Petroleum Industry Press,1997: 48-141.

[12] 趙先進, 姜青梅. 用動能因子確定產水氣井合理工作制度[J].斷塊油氣田, 1996, 3(4): 64-67.Zhao Xianjin & Jiang Qingmei. Determining reasonable working rules for water productiongas wells with the kinetic energy factor[J]. Fault-Block Oil & Gas Field, 1996, 3(4): 64-67.

[13] 曹光強, 李文魁, 嚴弦, 李雋, 唐卿. 氣井臨界流量計算模型的優選[J]. 石油鉆采工藝, 2011, 33(1): 53-55.Cao Guangqiang, Li Wenkui, Yan Xian, Li Juan & Tang Qing.Study on the gas well critical rate model optimize[J]. Oil Drilling& Production Technology, 2011, 33(1): 53-55.

[14] 李相鵬, 鄭水華. 逆向氣流對規整填料表面液膜流體動力學特性的影響[J]. 化工學報, 2013, 64(9): 3130-3138.Li Xiangpeng & Zheng Shuihua. Influences of counter-current gas ぼow on hydrodynamics of liquid ベlm over structured packing surface[J]. CIESC Journal, 2013, 64(9): 3130-3138.

[15] 章梓雄, 董曾南. 粘性流體力學[M]. 北京: 清華大學出版社,1998: 352-359.Zhang Zixiong & Dong Zengnan. Viscous fluid mechanics[M].Beijing: Tsinghua University Press, 1998: 352-359.

[16] 婁樂勤, 耿新中. 氣井攜液臨界流速多模型辨析[J]. 斷塊油氣田, 2016, 23(4): 497-500.Lou Leqin & Geng Xinzhong. Models of the critical liquid carrying ぼow rate for gas wells[J]. Fault-Block Oil and Gas Field,2016, 23(4): 497-500.

[17] 宋鵬舉. 氣體攜液能力的液體臨界含量實驗研究[D]. 西安:西安石油大學, 2013: 34-76.Song Pengju. Content of the experimental study of the gas liquid critical liquid carrying capacity[D]. Xi'an: Xi'an Shiyou University, 2013: 34-76.