考慮流固耦合的雙彎頭壓裂管匯的振動特性

祝效華 曾云義 陳 波 陶浩然

1.西南石油大學機電工程學院 2.中國石化廣元天然氣凈化有限公司

3.中國石化中原油田井下特種作業公司 4. 中國石油西南油氣田公司物資分公司

在頁巖氣開采過程中，通常需要借助大型體積壓裂實現高效開采[1]。在壓裂作業過程中，壓裂車泵出的壓裂液不均勻，在彎頭處壓裂液會對管壁產生隨時間變化的激振力，引起壓裂管匯產生耦合振動[2]。現場調研也反饋波動流和彎管導致的振動是引起壓裂管件疲勞破壞與源動力機械損壞的主要原因之一。針對管匯的振動問題，Pa?doussis等[3-4]建立了描述輸流管道非線性動力學行為的流固耦合振動模型，并分析了脈動流體對管道振動特性的影響規律；Ghayesh等[5]分析了彈性支撐對管道非線性振動特性的影響；Ghazali[6]討論了壓力變化對管匯振動的影響，并提出了幾種管線狀態監測技術；王琳等[7]用廣義積分法建立了輸流曲管動力學方程組，并計算了幾種典型邊界條件下的固有頻率及曲管失穩的臨界流速。以往分析基本針對于低壓情況下管匯的振動規律，計算結論不再適用于壓裂現場高壓或超高壓壓裂管匯的振動情況。為了減小管匯的振動、減少因振動誘發的工程事故，有必要開展彎頭在高壓條件下的振動分析研究。筆者推導了高壓彎管在各平面內的運動方程，編程計算了彎管振動強度隨各個參數變化的曲線。建立了彎管的單向流固耦合數值模型，通過現場實測數據驗證了數值模型的有效性，使用該模型計算了結構參數對雙彎頭彎管固有頻率的影響，為現場管匯的合理布局提供理論依據。

1 輸流彎管運動方程的推導

彎頭是連接兩條軸線不重合的直管段的管元件。壓裂液流經彎頭其流動方向發生變化，使脈動流的軸向慣性作用轉變成為壓裂液與內管壁的徑向耦合，從而產生振動。當壓裂液經過如圖1所示的雙彎頭時，振動強度遠大于單彎頭。因此，彎管處壓裂管線的振動除了來自于外部集中載荷作用，還要考慮流體與管線的流固耦合作用。

圖1 高壓壓裂現場雙彎頭布局圖

對彎管進行受力分析，采用微元法選取長為dl的微元段進行分析。令與彎管中心線相切的方向為z方向，垂直于彎管中心線所在平面為x方向，根據右手定則可以確定y方向的位置，三維直角坐標系與微元段所受到的力如圖2所示。假設計算模型為均質、各向同性的等截面彎管，流體也為均質的單一流體。忽略流體的內摩擦與流體與管壁的摩擦作用。流固耦合對地面管匯產生的扭轉作用非常小，扭轉振動基本可以忽略不計。因此暫不考慮彎管的扭轉。

圖2 彎管微元計算模型圖

對圖2中彎管微元段在軸向上進行受力平衡分析，根據牛頓第二定律得到彎管的受力平衡方程為：

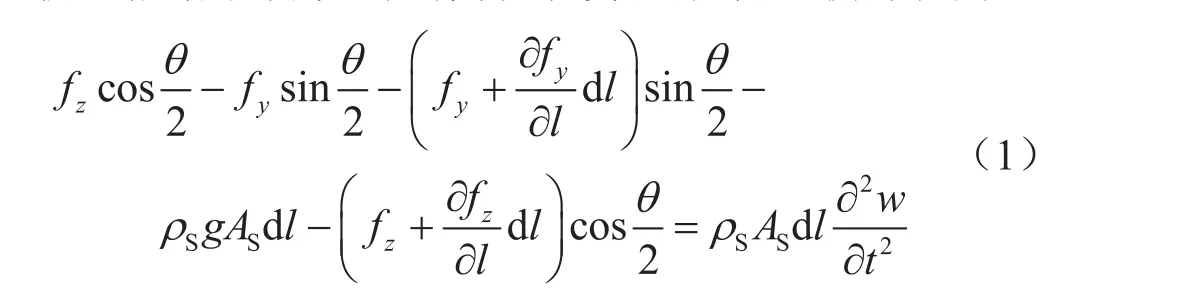
式中fx、fy、fz分別表示x、y、z方向上的作用力，N；ρS表示彎管材料的密度，kg/m3；AS表示彎管的橫截面積，m2；w表示彎管在z方向上的運動位移，m；l表示彎管長度，m。

由于管單元趨于無窮小，即θ為無窮小量，此時存在：

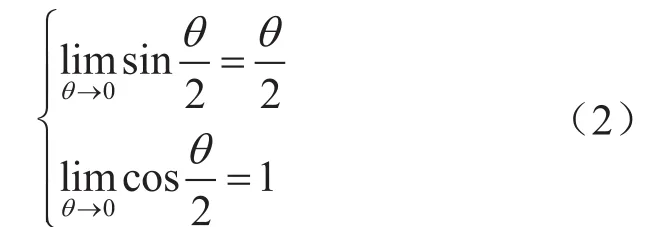
將式（2）代入式（1）進行化簡并忽略高階無窮小量可以得到彎管在軸向上的受力平衡方程為：

根據牛頓第二定律可以得到管內流體的受力平衡方程：

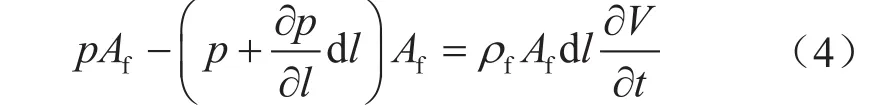
式中p表示流體的壓力，Pa；Af表示流體的橫截面積，m2；ρf表示壓裂液的密度，kg/m3；V表示流體的流動速度，m/s。

忽略高階無窮小量并化簡可以得到：

由圓弧彎管的弧長公式： 得到彎管的軸向應變為：

基于彈性力學理論得到彎管的物理方程為：

式中 表示彎管在z方向上的運動速度，m/s；h表示管壁的厚度，m； 表示流體流動的加速度，m/s2；μ表示彎管的泊松比；E表示彎管的彈性模量，Pa；R表示彎管軸線的半徑，m。

由于彎頭尺寸較大，管線長度較長，壓裂管線中流體在經過彎頭時流體的流動方向和形態被迫改變，流體壓力的作用對彎頭有“拉直”的效應，屬于“Bourdon”耦合，因此在考慮彎管的Bourdon效應[8]后得到等內徑彎管的連續方程為：

式中Kf表示由經典水及理論對流體狀態方程的假設確定的流體體積模量，Pa。

式（3）、（5）、（7）、（8）即為彎管在軸向上的流固耦合振動方程。

計算彎管在yz平面上的流固耦合振動方程則有：

彎管的力矩平衡方程為：

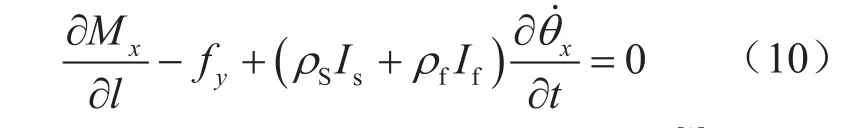
受Bourdon耦合影響的彎管的連續方程[9]為：

式中 表示彎管繞x軸的轉角速度，（°）/s；Y12表示彎管的壓力增大系數；Y13表示彎管的彎曲因子；Mx表示x軸的扭矩，N·m。

由彎管軸向位移產生的轉角的計算方程 為：

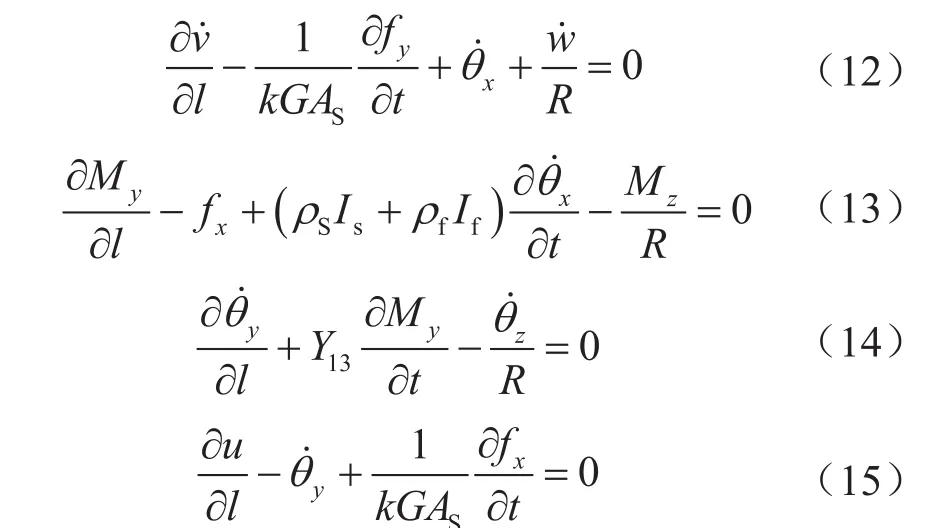
式中u、v分別表示管單元在x與y軸方向上的位移，m；Is與If分別表示彎管與流體截面的慣性矩，m4；G表示切變模量，分別表示彎管繞y、z軸的轉角速度，（°）/s；My、Mz分別表示y、z軸的扭矩，N·m。

由彎曲管線的平面運動方程解得的u、v、w是與位移和時間有關的解析解，彎管運動解析式可近似表達為：

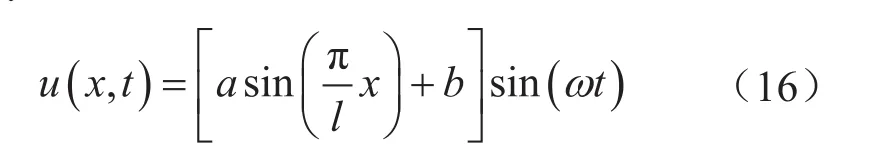
式中a表示彎管在兩端固定時的最大振幅，m；b表示隨著剛度的增大而減小常數值；ω表示彎管的振動頻率，Hz。

通過求解運動方程即可求得彎管的振動頻率與振動幅值。

由理論公式可以計算得到彎管在各個平面內的振動頻率與振動幅值，但是在計算時認為各個平面內的振動互不影響，且不考慮其他因素的影響，因此計算結果與實際測量會存在一定誤差。而隨著各個平面方向上振動強度增大，對其他平面方向振動影響也越大，因此由理論公式計算得到的彎管的振動頻率曲線與實際情況會存在一定誤差，振動頻率越高，相對誤差也會略有增大。因此需要驗證理論公式在壓裂現場的適用性，通過將壓裂管匯材料的物理參數與管內流體壓力為60 MPa等施工參數代入式（9）、（10）、（11）、（12）對y、z平面內彎管的振動頻率進行計算得到其振動頻率約為8.63 Hz，將其與現場圖3所示點測量數值進行對比可知管線振動頻率誤差最大約為17.02%。誤差小于20%，在工程中尚可接受該誤差，因此可以認為對壓裂管振動計算的理論公式基本適用于指導壓裂現場的振動計算。

壓裂管匯的共振會嚴重影響壓裂管件的使用壽命，為了防止管線共振，需要通過仿真方法計算壓裂管線的固有頻率從而在施工中使激振頻率避開壓裂管的固有頻率。

2 雙彎頭彎管數值模型建立與仿真分析

2.1 模型及參數

為了驗證仿真方法的可靠性，首先用設備狀態綜合分析系統與高頻振動探頭對中石油四川長寧天然氣開發責任有限公司長寧1號H10-2壓裂井隨機抽取多根壓裂管線的不同點對其垂直方向上的振動進行測量，測量點如圖3所示。

通過對壓裂車與交流管匯之間的管線進行長度尺寸的測量，利用三維軟件建立了如圖3-a所示壓裂車與交流管匯之間的管線仿真計算模型。根據對現場實用壓裂管切割制作標準件進行試驗得到壓裂管線密度為7 850 kg/m3，彈性模量（E）為209 GPa，泊松比為0.3，管線內徑（d）為70 mm，直管壁厚（h1）為11 mm，彎管壁厚（h2）為19 mm。并在圖2所建立的坐標系內對彎頭在yz平面上的振動頻率利用ANSYS Workbench軟件進行分析計算，基于現場流速排量的計算，仿真計算時設置管內流速為壓裂車出口處壓力為60 MPa。選取彎頭處的計算點與振動方向如圖4中箭頭所示，位置與方向與圖3-b中的測量點的位置基本相同。

由于壓裂管線抗拉剛度較大，其沿徑向或軸向上變形量較小，但是在作業過程中壓裂液與管壁摩擦產生的壓降較大，因此在仿真過程中采用摩擦耦合的方式進行計算，并在此基礎上以壓裂車的振動頻率作為管匯諧響應激振頻率。

對圖4所示模型中箭頭所示點進行仿真計算，所得結果與高頻振動探頭測量圖3-b所示振動測量點的振動頻率與振動幅值進行對比，結果如圖5所示。

由圖5所示仿真計算結果與現場測量結果進行對比可看出，該點振動在10 Hz時彎管的振動幅值出現峰值約為0.505 63 mm，現場測量的該點的振動頻率約10.4 Hz時出現振幅峰值為0.35 mm，振動幅值相差約為0.15 mm，這是由于壓裂現場所使用的管道無法完全實現不同位置的材料均勻性與各向力學特性均保持不變，且壓裂現場施工環境復雜，外界對管道振動存在較強的干擾以及在對管道振動強度進行現場測量的過程中誤差等因素的存在，導致壓裂現場測量所得諧響應頻率與激振頻率之間存在一定誤差，但誤差在可接受范圍內，而由于仿真計算過程中不存在以上任何因素的干擾。因此計算所得諧響應頻率與激振頻率保持一致。由振動幅值的對比分析可以得知振動幅值可知，模型的計算振幅要略大于管道的測量振幅，且誤差值約為22.1%。這是由于在壓裂現場不存在完全固定，在對模型出入口兩端施加固定約束與現場實際情況存在一定誤差，可以認為誤差在合理范圍內。因此可以認為仿真計算方法可以用于計算管匯的固有頻率與諧振頻率。

圖3 連接頭處測量點與直管中間測量點照片

圖4 仿真計算模型與計算點圖

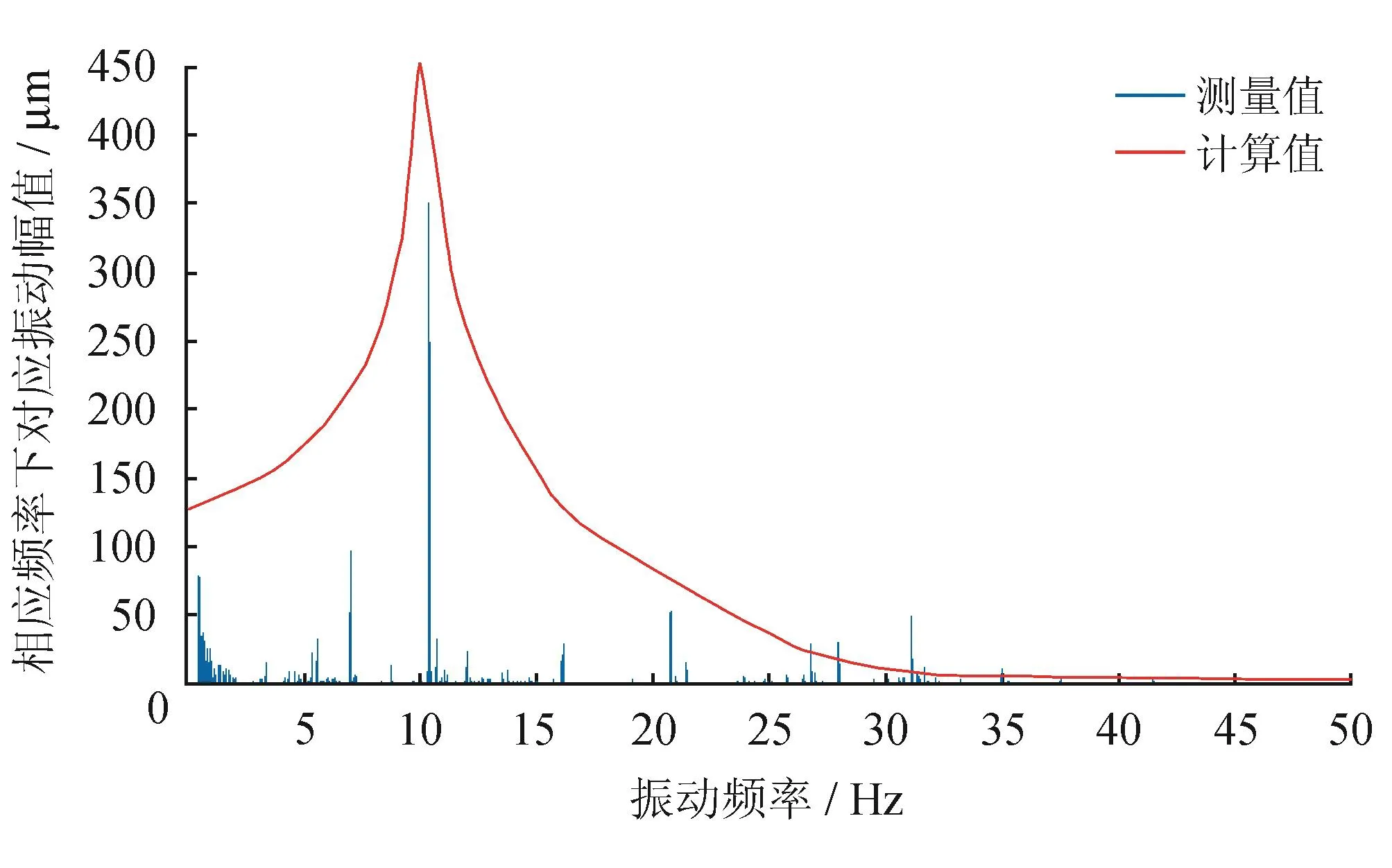
圖5 仿真計算結果與測量結果對比圖

為了減小仿真計算誤差，使方程更加容易收斂，模型使用六面體劃分網格，由于壓裂液與管匯之間的作用狀態可以認為是固液處于可分離狀態、切向處于可滑動狀態且只有一個接觸面。因此采用Frictional固液表面非對稱接觸的接觸類型[10]，進而得到如圖6所示的帶網格的雙彎頭彎管模型。

圖6 雙彎頭彎管模型與網格圖

如圖6所示的壓裂管在保持壁厚不變的情況下可生成多種管線內徑。彎頭相連的直管的長度為2 m，兩條支管之間所成的角度即兩個彎頭的連接角度可變。然后對模型進行流體填充，劃分網格，并對流體與管內壁接觸的邊界層的網格進行膨脹層處理。壓裂管中采用水作為流體介質。整個分析中不考慮溫度對流固耦合的影響。

2.2 數值分析方法

雙彎頭彎管流固耦合振動采用ANSYS Workbench—Fluent軟件進行求解。在分析彎管模型流固耦合振動的模態時對模型的兩端都約束6個方向的自由度，即添加固定約束。根據壓裂現場實際情況，在模型左端流體的入口處將壓裂液簡化為正弦波動的連續流體，出口處的壓力簡化為60 MPa的常壓，由于壓裂彎管的抗拉剛度較大，在實際工作過程中壓裂液對壓裂管道的“拉直量”非常小。因此，在仿真計算過程中為了節約計算資源，忽略了管道的拉直效應，在雙彎頭處只考慮流固耦合不考慮彎頭的Bourdon耦合效應，并對流體與壓裂管的接觸面添加相同的流固耦合標簽。整個模型仿真過程的流固耦合通過此耦合面完成。由Fluent對流場進行分析，將計算得到的流場壓力作為載荷直接添加到彎管的流固耦合面對壓裂管的振動進行分析, 由于壓裂管線的振動對流場中高壓高速的流體影響較小，基本可以忽略不計。因此計算時為了能夠節約計算資源采用單向流固耦合的算法[11]，整個分析過程經過若干次迭代后收斂。

在計算的過程中為了節約計算資源，可以適當增大單元格的大小，并減小計算的時間步長，但是為了使流固耦合計算容易收斂的單元格不能太大，因而在計算過程中要不斷調整網格的大小，使其達到最合理的質量。因此計算采用分步式計算的方法來獲取相對較短的計算時間[12]。

2.3 不同因素對固有頻率的影響

2.3.1 流固耦合

為了分析流固耦合對管匯固有頻率的影響，計算了雙彎頭內徑為70 mm，連接角度為90°時空管與脈動流體流經雙彎頭彎管的前六階固有頻率，將其進行對比得到的計算結果如表1所示。

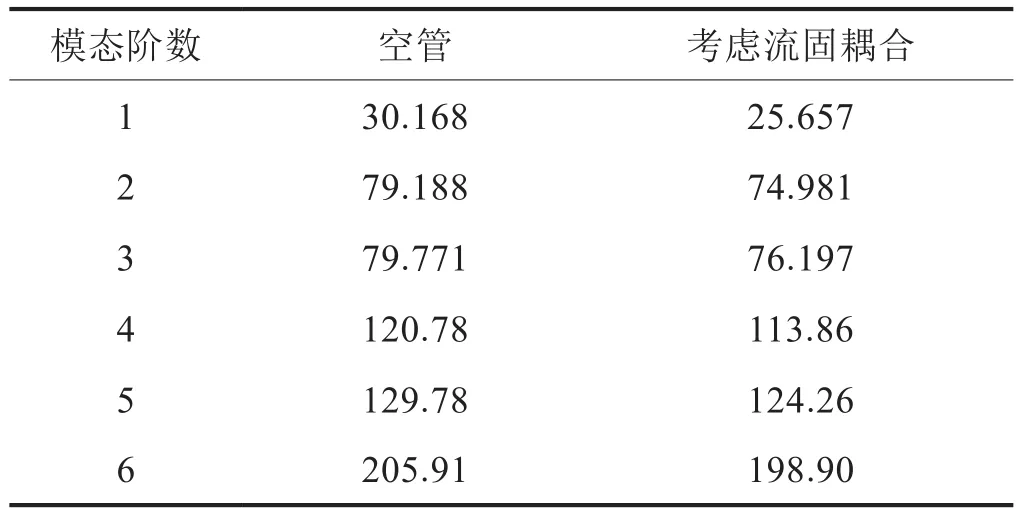
表1 雙彎頭的固有頻率表 Hz

對表1進行分析對比可得知：在考慮模型的流固耦合作用時雙彎管的固有頻率比空管的固有頻率明顯降低。這是因為在當雙彎管只對出入口進行固定支撐時由于管匯的支撐較少導致雙彎管與管內流體耦合作用增強，從而對管匯因外力引起的振動響應計算產生較大的影響。因此在對雙彎頭彎管進行仿真計算時考慮流固耦合的作用是非常有必要的。

2.3.2 連接角度對雙彎頭彎管固有頻率的影響

在流速與流體壓力都相同的情況下，計算了內徑為70 mm的雙彎頭的連接角度對雙彎頭彎管固有頻率的影響。由于流體的脈動頻率與外部的激振頻率比較低，因此只提取前兩階模態進行分析，同時，為了對比計算雙彎頭彎管連接角度介于75°～105°的減振效果，采用了與模型驗證相同的諧響應頻率分析方法在彎管的入口處添加了一個激振頻率，通過分析計算得到雙彎頭的連接角度與固有頻率及諧響應振動幅值的關系，如圖7所示。

圖7 雙彎頭固有頻率與振動幅值隨連接角度變化圖

由圖7可看出，隨著雙彎頭連接角度的不斷增大，一階固有頻率呈現非線性遞增的趨勢，但增幅較小，可近似認為雙彎頭連接角度對一階固有頻率的變化影響不大；而二階固有頻率隨著連接角度的增大出現先增大后減小的趨勢，且在90°左右時出現最大值，即在壓裂現場存在較低激振頻率時，雙彎頭的連接角度控制在75°～105°的范圍內時更不容易引起彎管的共振。

由圖8可看出，彎管的諧響應振動幅值在90°附近時最低，將其與其他連接角度的振動幅值進行對比，將連接角度控制在90°附近時彎管的諧響應頻率最大可減小約30%。

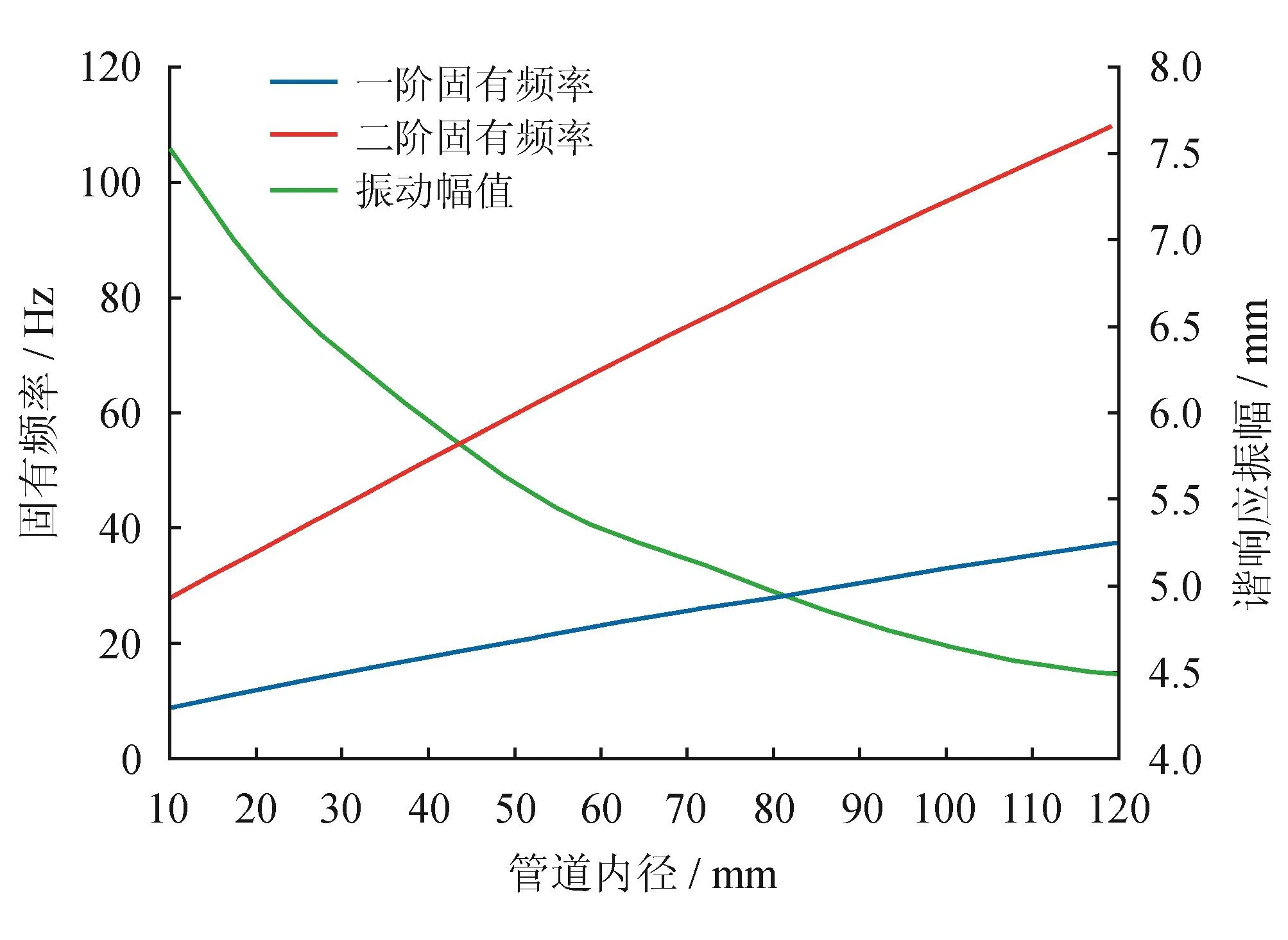
圖8 雙彎頭固有頻率隨內徑變化圖

因此兩個彎頭的連接角度介于75°～105°時彎管振動有明顯的減小，但由于一階固有頻率變化不大，若現場的激振頻率較低時仍需要考慮管匯系統與外載激勵的匹配以避免耦合共振[13]。

2.3.3 彎管內徑對雙彎頭彎管固有頻率的影響

在壁厚一定的情況下，對連接角度為90°的雙彎頭進行彎管內徑對固有頻率影響的分析計算，得到雙彎頭彎管內徑與其固有頻率及理論計算得到的彎管諧響應振動幅值的關系，如圖8所示。

在理論公式計算中需要利用面積公式將彎管內徑的變化轉化為橫截面積的變化才能進行計算。由圖8可看出，在考慮流固耦合的作用時，隨著彎管內徑的增大彎管的一階與二階固有頻率呈近似線性增大的趨勢，但是其增幅并不完全相同，且二階固有頻率隨著彎管內徑增大增幅比一階固有頻率增幅較大，即彎管的內徑對二階固有頻率的影響比一階固有頻率影響更大。隨著管徑的增大，壓裂彎管越不容易發生失穩現象。且由理論計算得到的彎管諧響應振動幅值曲線可看出，隨著彎管內徑的增大彎管的諧響應振動幅值呈現類似指數下降的趨勢，即隨著彎管內徑的增大，減振效果也逐漸減弱，由計算結果可看出：在60 MPa壓力下，彎管內徑在100 mm左右時，振動幅值逐漸趨于平穩，較彎管內徑為70 mm時振動幅值減小約20%。

2.3.4 曲率半徑對雙彎頭彎管固有頻率的影響

為了分析彎管處的曲率半徑對固有頻率的影響，分析了彎管內徑為70 mm，壁厚為19 mm的雙彎管在不同曲率半徑下的固有頻率，得到彎管的曲率半徑對管道前兩階固有頻率與諧響應振動幅值的影響曲線（圖9）。

圖9 雙彎頭固有頻率隨彎管曲率半徑變化圖

由圖9可看出，隨著彎管曲率半徑的增大，雙彎管的一階固有頻率減幅較小，基本保持不變，二階固有頻率隨曲率半徑的增大呈近似非線性減小的趨勢，曲率半徑超過180 mm以后趨于平緩，而且由圖9可看出，隨著彎管曲率半徑的增大，其振幅明顯減小。這是由于流體流過彎頭時，由于離心力的作用，壓裂液的壓力集中在彎管外側壁附近，隨著彎管曲率半徑的增大，其壓強作用面積也相應增大，而彎管外側壁壓強最大值逐漸減小，且隨著曲率半徑的增大，形成湍流所需時間增加，彎管受到的不穩定壓力增大[14]，因此雙彎頭彎管的固有頻率會逐漸減小，而振幅也會由于最大壓強值的減小而逐漸減小[15]。且由理論計算結果可知，諧響應振動幅值隨著彎管曲率半徑的增大逐漸減小，但減幅較小減小，對管道振動強度的影響不大。

由此可見，彎管的曲率半徑是影響壓裂管線的固有頻率的另一個重要因素。因此對計算結果進行分析可得知，在管匯布局允許的情況下，為了防止彎管振動強度過大，應該在考慮減小彎管的振動強度的同時避開彎管的固有頻率，而且為了防止由于彎管曲率半徑過小而出現應力集中于彎頭凸壁而導致彎頭受力不均振幅增大的情況，彎頭的曲率半徑不宜過大或太小應該盡量控制在160 mm左右。

3 結論

1）在流固耦合作用下，雙彎頭彎管的連接角度對彎管的穩定性存在較大的影響，壓裂現場應該將兩個彎頭的連接角度盡量控制在75°～105°，彎管的振動強度最大可減小約30%。連接角度太大或太小都會使雙彎管固有頻率偏低而導致彎管容易在激振力的作用下引起共振。

2）在流固耦合的作用下，雙彎頭彎管的固有頻率隨彎管內徑的增長呈近似線性增長的關系，壓裂現場應盡量選擇內徑約為101.4 mm左右的壓裂管線。

3）雙彎頭彎管中存在脈動流體時，彎管的曲率半徑對雙彎頭彎管的固有頻率與振動幅值都存在較大影響。為使彎管保持穩定，減小管匯的振動強度，在壓裂現場激振頻率不高的情況下，彎管內徑為70 mm時，彎管的曲率半徑應該盡量控制在160 mm左右。

[1] Tan JQ, Weniger P, Krooss B, Merkel A, Horsベeld B, Zhang JC,et al. Shale gas potential of the major marine shale formations in the Upper Yangtze Platform, South China, Part II: Methane sorption capacity[J]. Fuel, 2014, 129: 204-218.

[2] Tijsseling AS. Fluid-structure interaction in liquid-ベlled pipe systems: A review[J]. Journal of Fluids and Structures, 1996, 10(2):109-146.

[3] Pa?doussis MP & Li GX. Pipes conveying ぼuid: A model dynamical problem[J]. Journal of Fluids and Structures, 1993, 7(2): 137-204.

[4] Tubaldi E, Amabili M & Pa?doussis MP. Fluid–structure interaction for nonlinear response of shells conveying pulsatile ぼow[J].Journal of Sound and Vibration, 2016, 371: 252-276.

[5] Ghayesh MH. Parametric vibrations and stability of an axially accelerating string guided by a non-linear elastic foundation[J].International Journal of Non-Linear Mechanics, 2010, 45(4): 382-394.

[6] Ghazali MH, Hee LM & Leong MS. Piping vibration due to pressure pulsations: Review[J]. Advanced Materials Research, 2014,845: 350-354.

[7] 王琳, 倪樵, 黃玉盈. GDQR法用于輸流曲管的流致振動研究[J]. 動力學與控制學報, 2005, 3(1): 72-77.Wang Lin, Ni Qiao & Huang Yuying. GDQR for the analyses ofぼow-induced vibrations of curved pipes conveying ぼuid[J]. Journal of Dynamics and Control, 2005, 3(1): 72-77.

[8] Tentarelli SC. Propagation of noise and vibration in complex hydraulic tubing systems[D]. Bethlehem: Lehigh University, 1991.

[9] 李艷華. 考慮流固耦合的管路系統振動噪聲及特性研究[D].哈爾濱: 哈爾濱工程大學, 2011.Li Yanhua. Study on vibration and noise and its characteristics of pipeline systems considering ぼuid-structure interaction[D] Harbin: Harbin Engineering University, 2011.

[10] Wang J, Hua H & Gu CS. On the correction of the boundary de-ベciency in SPH for the frictional contact simulation[J]. Science China Technological Sciences, 2014, 57(1): 86-100.

[11] 顧嬡, 酈鳴陽, 沈力行, 喻洪流, 丁皓, 趙改平. 狹窄動脈流固耦合模型ANSYS/CFX數值的有限元分析[J]. 中國組織工程研究與臨床康復, 2008, 12(52): 10293-10296.Gu Yuan, Li Mingyang, Shen Lixing, Yu Hongliu, Ding Hao &Zhao Gaiping. Finite element analysis of stenosed artery-blood coupling model in ANSYS/CFX[J]. Journal of Clinical Rehabilitative Tissue Engineering Research, 2008, 12(52): 10293-10296.

[12] Kuehlert K, Webb S, Schowalter D, Holmes W, Chilka A & Reuss S. Simulation of the ぼuid–structure-interaction of steam generator tubes and bluff bodies[J]. Nuclear Engineering and Design, 2008,238(8): 2048-2054.

[13] 付永領, 荊慧強. 彎管轉角對液壓管道振動特性影響分析[J].振動與沖擊, 2013, 32(13): 165-169.Fu Yongling & Jing Huiqiang. Elbow angle effect on hydraulic pipeline vibration characteristics[J]. Journal of Vibration and Shock, 2013, 32(13): 165-169.

[14] Abhari MN, Ghodsian M, Vaghefi M & Panahpur N. Experimental and numerical simulation of ぼow in a 90°bend[J]. Flow Measurement and Instrumentation, 2010, 21(3): 292-298.

[15] Mirzaei M, Najafi M & Niasari H. Experimental and numerical analysis of dynamic rupture of steel pipes under internal high-speed moving pressures[J]. International Journal of Impact Engineering, 2015, 85: 27-36.