基于多模型MCP方法的洪水概率預報

王艷蘭 梁忠民 王凱 羅俐雅

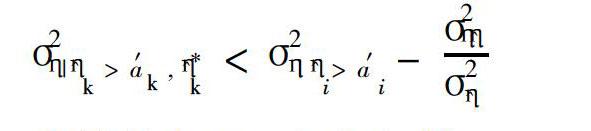
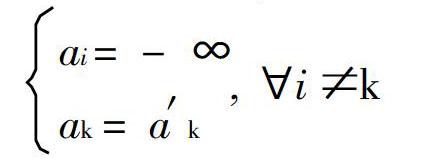
摘要：洪水概率預報通過提供具有一定置信度的預報區間，評估預報結果的可靠度，為防洪調度提供重要依據。以淮河關鍵防洪斷面王家壩為研究對象，分別采用API和新安江（XAJ）確定性模型進行初始的確定性預報，在此基礎上，再采用模型條件處理器（MCP）推求不同量級洪水預報流量的條件概率分布函數，實現洪水概率預報。分別從中位數的確定性精度評價和概率預報的可靠度評價兩方面對預報結果進行分析，結果表明：MCP洪水概率預報結果不僅具有較高的可靠度，而且其中位數預報與確定性模型結果相比，預報精度整體有所提高，說明MCP具備一定的校正預報能力。

關鍵詞：洪水概率預報;模型條件處理器;API模型;新安江模型

中圖分類號：TV122.5文獻標志碼：A開放科學（資源服務）標識碼（OSID）：王艷蘭

Probabilistic flood forecasting based on multi-model MCP

WANG Yanlan.1，LIANG Zhongmin.1，WANG Kai.2，LUO Liya.3

（1.College of Hydrology and Water Resources，Hohai University，Nanjing 210098，China;

2.Bureau of Hydrology，Huaihe Water Conservancy Committee，Bengbu 233001，China;

3.Jiangsu Province Hydrology and Water Resources Investigation Bureau，Nanjing 210098，China）

Abstract：The probabilistic flood forecasting can provide a prediction interval with a certain reliability，and can be used to evaluate the reliability of forecasting results.It can provide an important basis for flood control scheduling.We took Wangjiaba cross-section，a key flood control section of Huaihe River，as the research object.Based on the prediction results of API and XAJ models，using the Model conditional processor （MCP） to deduce the conditional probability distribution function of the forecasting runoff of floods of different magnitudes，we realized probabilistic flood forecasting.The prediction results were analyzed in terms of the deterministic precision evaluation of median number and the reliability evaluation of probabilistic forecasting.The results showed that the MCP probabilistic flood forecasting has a high reliability，and its median number prediction has a higher prediction accuracy than the deterministic model，indicating that MCP has a certain ability of correction and prediction.

Key words：probabilistic flood forecasting;model conditional processor;API model;Xin′anjiang model

洪水預報主要是通過水文模型得到一種確定性的定值預報，但水文模型都是對水文物理過程的近似，其預報結果必然具有不確定性[1-2]，洪水概率預報可定量描述預報結果的不確定性，不僅給出置信區間以評估洪水預報的可靠度，還能以分位數形式（如均值或中位數）提供類似于傳統方法的定值預報，使得預報信息更為完整[3-4]。

在洪水概率預報中，貝葉斯方法得到廣泛的研究與應用[5-10]。其中，水文不確定性處理器[11-12]（Hydrologic Uncertainty Processor，HUP）是一種最常用的概率預報方法，該處理器以確定性模型為基礎，利用貝葉斯公式估計預報變量的概率分布以實現洪水概率預報。洪水預報實踐表明，一般很難存在一個模型能在任何情況下都提供始終優于其他模型的預報結果，也說明洪水預報模型的選擇存在不確定性[7];而貝葉斯模型平均法[13-14]（Bayesian model averaging，BMA）是一種基于貝葉斯理論綜合不同模型預報結果的分析方法，可發揮不同模型的優勢，提供更可靠的預報結果，因此也得到了廣泛應用[15]。研究發現，不同量級的洪水預報誤差存在差異性[16-17]，即暴雨中心位置不同、洪水量級不同、漲落水不同階段，洪水預報誤差的規律也往往不同;模型條件處理器（Model Conditional Processor，MCP）[18-19]方法可通過聯合分布來處理場次洪水預報誤差的異分布問題，所以使其比HUP更適用于評估洪水預報的不確定性;此外，MCP方法不再局限于只選擇一個確定性模型，而是與BMA類似，可對多個模型預報結果進行綜合分析，因此該方法可看做是HUP和BMA的概括和總結[20]。

本文在API模型[21]和新安江（XAJ）模型[22]預報結果的基礎上，采用MCP方法對淮河王家壩斷面進行洪水概率預報研究。

1方法原理

1.1多模型MCP原理

模型條件處理器（MCP）是結合實測資料與確定性水文模型預報結果的聯合概率分布，通過正態分位數轉換，[JP+2]將預報不確定性轉換至正態空間，根據貝葉斯理論推求預報變量的條件概率分布函數。

假設y表示實測變量，[AKy^D]表示初始水文模型的預報變量，將y和[AKy^D]通過正態分位數轉換得η和[AKη^D]。在正態空間里，η和[AKη^D]的聯合分布可假設為正態二元分布f（η，[AKη^D]），預報不確定性用以初始預報值為條件的預報量的概率密度函數表示：

其均值和方差為：

MCP可通過將二元正態分布推廣到多元正態分布的方法來綜合多個確定性模型的預報結果。假設有M個確定性模型，則將M個模型預報值[AKy^D]i（i=1，… ，M）轉換到多元正態空間得[AKη^D]i。每個變量在正態空間里都對應一個標準正態分布和預報不確定性，即以M個模型的預報值為條件的預報量的分布可以表示為（y|[AKy^D]1，…，[AKy^D]M），轉換值的條件分布可分別縮寫為f（η|[AKη^D]i），

均值、方差如下：

式中，∑η[AKη^D] 和∑[AKη^D][AKη^D]分別為

1.2多模型分段聯合正態分布

已有研究表明[16]，不同量級洪水預報誤差的分布會有所不同，這等價于η和[AKη^D]的關系可能隨流量量級而變化。所以，可以根據η和[AKη^D]的關系圖，發現不同量級流量的分布規律不同，再采用截斷正態分布（TNDs）分別描述不同流量量級初始預報值與實測值的關系，即根據分界點a，可將正態空間的聯合分布分為兩個（或多個）TNDs。

當[AKη^D]>a時，其截斷的正態分布為

f（[AKη^D]|[AKη^D]>a）=[SX（]f（[AKη^D]）[]

∫.+∞af（[AKη^D]）d[AKη^D][SX）]=[SX（]f（[AKη^D]）[]1-F[AKη^D]（a）[SX）]（5）

根據貝葉斯理論，截斷后的預報不確定性可表示為以初始預報值[AKη^D].*>a為條件的η的條件概率密度函數：

f（η|[AKη^D]>a，[AKη^D].*）=[SX（]f（η，[AKη^D]|[AKη^D]>a，[AKη^D].*）[]f（[AKη^D]|[AKη^D]>a，[AKη^D].*）[SX）]=[SX（]f（η，[AKη^D]|[AKη^D].*）[]f（[AKη^D]|[AKη^D].*）[SX）]（6）

均值和方差為

[JB（]μη|[AKη^D]>a，[AKη^D].*=μη+[SX（]ση[AKη^D][]σ..2[AKη^D][SX）]（[AKη^D].*-μ[AKη^D]）

σ..2η|[AKη^D]>a，[AKη^D].*=σ..2η-[SX（]σ..2η[AKη^D][]σ..2[AKη^D][SX）][JB）]（7）

式中：μη、μ[AKη^D]分別為η|[AKη^D]>a和[AKη^D]|[AKη^D]>a條件下分布的均值;ση、σ[AKη^D]為標準差。

當結合多個模型預報值時，因每個模型都有對應的臨界值，為確定具有代表性的樣本，將每個模型高流量部分期望值的方差進行比較，以方差較小的模型的臨界值作為多元聯合分布分段的依據。

設a′i表示模型正態分布分段的臨界值，σ..2η|[AKη^D]i=[AKη^D].*i>a′i表示模型正態分布上部的條件方差，向量[WTHX][AKη^D]表示模型的模擬變量

選定更能代表高流量部分的模型k[WTBX]，即：

σ..2η|[AKη^D]k[WTBX]>a′k[WTBX]，[AKη^D].*k[WTBX]<σ..2η|[AKη^D]i>a′i-[SX（]σ..2η[AKη^D][]σ..2[AKη^D][SX）]

為簡單起見，定義向量[WTHX]a[WTBX]：

[JB（{]ai=-∞ak[WTBX]=a′k[WTBX][JB）]，i≠k[WTBX]

預報不確定性可表示為以[AKη^D].*>ak[WTBX]為條件的η的條件概率密度函數：[HJ1.8mm]

f（η|[AKη^D]k[WTBX]>ak[WTBX]，[AKη^D].*）=[SX（]f（η，[AKη^D]|[AKη^D]k[WTBX]>ak[WTBX]，[AKη^D].*）[]f（[AKη^D]|[AKη^D]k[WTBX]>ak[WTBX]，[AKη^D].*）[SX）]=[SX（]f（η，[AKη^D]|[AKη^D].*）[]f（[AKη^D]|[AKη^D].*）[SX）]（8）

其均值和方差為

[JB（]μη|[AKη^D]k[WTBX]>ak[WTBX]，[AKη^D].*=μ+∑η[AKη^D] ∑.-1[AKη^D][AKη^D]（[AKη^D]..*-[AKμ^D]）

σ.2η|[AKη^D]k[WTBX]>ak[WTBX]，[AKη^D].*=∑η[AKη^D]-∑η[AKη^D] ∑.-1[AKη^D][AKη^D]

∑..Tη[AKη^D]

[JB）]（9）

式中：∑ηη=1，μ、[AKμ^D]分別表示η|[AKη^D]k[WTBX]>ak[WTBX]和[AKη^D]|[AKη^D]k[WTBX]>ak條件下分布的均值。

[JP+2]通過對預報量的條件概率分布進行逆轉換，可得其任一分位數在原始空間中對應的預報流量值。

[BT2-*6]2應用實例

[JP+2]王家壩站是淮河干流上的主要控制站，其控制流域面積為30 630 km.2，降水量具有時空分布不均勻，年際變化大等特點。本文采用MCP方法結合API模型和新安江模型的預報結果，實現王家壩斷面的洪水概率預報。研究流域示意圖見圖1。

2.1基于API模型的確定性預報

淮河王家壩斷面的洪水主要是由息縣、潢川和班臺的河道來水以及息潢班～王家壩區間洪水兩部分組成。息縣、潢川和班臺洪水河道匯流采用馬斯京根法;息潢班～王家壩區間的產流計算采用降雨徑流相關圖法，匯流采用單位線法。選取1990-2010年間18場洪水資料進行模型計算（其中14場率定，4場用于驗證），Δt=2 h，預報精度見表1。

由表1可知，API模型率定期和驗證期的確定性系數均大于0.7，部分場次洪水的洪峰誤差和洪量誤差超過了20%的許可誤差[23]。究其原因，API模型是以經驗為主的產匯流模型，在水源劃分、河網匯流等環節上都存在人為性，且無法考慮降雨分布的不均勻性。

2.2基于新安江模型的確定性預報

選用1990-2010年的資料進行日模型計算，采用上述18場洪水資料進行次洪模型計算（其中14場率定，4場用于驗證），Δt=2 h，預報精度見表2。

由表2可知，新安江模型預報精度較高，18場洪水的確定性系數均大于0.7，洪量和洪峰誤差均在許可誤差以內。

2.3MCP方法應用

通過正態分位數轉換后，API模型預報值[AKy^D]1、新安江模型預報值[AKy^D]2與實測值得到其轉換值[AKη^D]1、[AKη^D]2和η。如圖2所示，在正態空間中，[AKη^D]1和η、[AKη^D]2和η的點據大體呈現出兩種不同的分布規律，其中，（a）中點據大概以a=1.8為分界點，（b）中點據大概以坐標原點為分界點;分段估計以[AKη^D]為條件η的概率分布，各段分布的均值隨流量大小的變化而改變。采用分位數回歸[24]分別對其進行回歸分析，圖中給出的是5%、50%及95%分位數下的回歸結果，即中位數及90%置信度的預報區間。

2.4結果分析

2.4.1基于分位數的確定性精度評價

將上述18場洪水確定性模型的預報結果以及實測資料作為MCP方法的輸入進行王家壩斷面的洪水概率預報。此方法可求得各時刻流量的條件分布函數和各分位點的估值，類似于確定性預報，提供50%分位數的估計值作為定值預報。基于分位數的確定性精度評價如下：

（1）確定性系數。

如圖3所示，基于單個確定性模型的MCP方法（MCP-API、MCP-XAJ）得出的中位數預報結果與確定性模型結果相比，確定性系數都有所提高;結合兩個確定性模型的MCP方法（MCP-API+XAJ），其確定性系數最高。

（2）洪峰誤差。

如圖4所示，從洪峰誤差來看，MCP方法預報洪峰結果比確定性模型更接近實測洪峰，且MCP-API+XAJ的洪峰誤差最小。

（3）洪量誤差。

如圖5所示，API的洪量誤差最大，MCP-API和MCP-XAJ的洪量誤差相比于原模型都有所減小，且MCP-API+XAJ減小的最明顯。

綜上，MCP方法提供的中位數預報結果，其確定性系數、洪峰誤差和洪量誤差都整體優于確定性模型，且MCP結合兩個確定性模型時，其預報結果最優，表明MCP方法具有校正預報功能。

2.4.2概率預報的可靠度評價

MCP方法提供了洪水過程的中位數預報及預報區間（置信度為90%）的估計結果，并采用區間覆蓋率以及離散度指標對概率預報的可靠度進行評估[25]。區間覆蓋率越大、離散度越小說明模型預報的不確定性越小，但這兩個指標往往無法同時達到最優。

由圖6可知，基于單個模型的MCP中位數預報結果無法保證某一個模型的覆蓋率和離散度能同時達到最優，而基于兩個模型的MCP方法，其預報區間（置信度為90%）平均覆蓋率達到87%，且離散度明顯降低，平均值達0.51，即在相對較小的預報區間寬度內，仍能夠覆蓋絕大多數實測數據，說明綜合兩個模型的MCP中位數預報結果可靠度更高。

2.4.3場次洪水結果分析

因篇幅有限，選取了其中三場具有代表性的洪水（包括小洪水、大洪水、復峰洪水）進行結果分析，MCP洪水概率預報結果見表3，圖7為19910612號、19980801號和19990622號次洪MCP中位數及90%置信區間預報結果。

表3依次列出了三場典型洪水MCP-API、MCP-XAJ和MCP-API+XAJ的概率預報結果。由表可知，19910612號洪水（大洪水）的確定性系數呈現出依次增大的趨勢，即MCP-API+XAJ的確定性系數最高，其洪峰誤差和洪量誤差最小，預報區間（置信度為90%）的覆蓋率最高，且離散度也最小;19980801號洪水（復峰洪水），MCP-XAJ的洪峰誤差最小，預報區間覆蓋率最高，但其離散度也最大，而MCP-API+XAJ的確定性系數最高，其離散度也最小;19990622號洪水（小洪水），MCP-XAJ的[CM（22]洪峰誤差和洪量誤差最小，但圖7場次洪水MCP中位數及90%置信區間預報結果確定性系數最高，且預報區間（置信度為90%）的覆蓋率最高，離散度也相對較小。

綜上，不管是從基于分位數的確定性精度評價指標來看，還是從概率預報的可靠度評價指標來看，MCP-API+XAJ的預報結果都優于MCP-API和MCP-XAJ，究其原因，是由于MCP-API+XAJ不僅結合了實測資料，還合成了兩個確定性模型的預報結果，并利用貝葉斯理論進行修正，使得其中位數預報結果更接近于流量實測值，以此提高了洪水預報的可靠度。

3結論

本文將多模型條件處理器（MCP）應用于淮河王家壩斷面的洪水概率預報。對18場洪水的分析表明，預報相對誤差隨流量量級的增大而減小，即不同量級洪水預報誤差分布規律不同，所以采用MCP分段估計洪水預報的不確定性并實現概率預報。若將MCP概率預報50%分位數（中位數）作為洪水過程的定值預報，其精度整體上高于單一的確定性模型預報結果，這是因為MCP屬于貝葉斯框架下的方法，具有融合先驗和樣本信息生成后驗信息的功能，反映在洪水預報問題上，該方法具有一定的校正能力，所以預報精度有所提高;而且，MCP的多模型綜合降低了單個模型預報的不確定性，相同置信度下其預報區間的覆蓋率更高、離散度更低。

參考文獻（References）：

[1]葉守澤，夏軍.水文科學研究的世紀回眸與展望[J].水科學進展，2002，13（1）：93-104.（YE S Z，X J.Century′s retrospect and looking into the future of hydrological science[J].Advancesin Water Science，2002，13（1）：93-104.（in Chinese）） ?DOI：10.3321/ j.issn：1001-6791.2002.01.017.

[2]梁忠民，戴榮，李彬權.基于貝葉斯理論的水文不確定性分析研究[J].水科學進展，2010，21（2）：274-281.（LIANG Z M，DAI R，LI B Q.A review of hydrological uncertainty analysis based on Bayesian theory[J].Advances in Water Science，2010，21（2）：274-281.（in Chinese））

[3]盧迪，彭勇，徐煒，等.氣象集合預報在水文領域中的應用研究進展[J].南水北調與水利科技，2014（2）：116-119.（LU D，PENG Y，XU W，et al.Research progress on hydrological application of meteorological ensemble forecast[J].South-to-North Water Transfers and Water Science & Technology，2014（2）：116-119.（in Chinese）） DOI：10.13476/ j.cnki.nsbdqk.2014.02.027.

[4]徐興亞，方紅衛，張岳峰，等.河道洪水實時概率預報模型與應用[J].水科學進展，2015，26（3）：356-364.（XU X Y，FANG H W，ZHANG Y F，et al.A real-time probabilistic channel flood forecasting model and application based on particle filters[J].Advances in Water Science，2015，26（3）：356-364.（in Chinese）） DOI：10.14042/ j.cnki.32.1309.2015.03.007.

[5]張宇，梁忠民.BFS在洪水預報中的應用研究[J].水電能源科學，2009，27（5）：44-47.（ZHANG Y，LIANG Z M.Application research of BFS to flood forecasting[J].Water Resources and Power，2009，27（5）：44-47.（in Chinese）） DOI：10.3969/ j.issn.1000-7709.2009.05.014.

[6]王善序.貝葉斯概率水文預報簡介[J].水文，2001，21（5）：33-34.（WANG S X.Introduction on probability hydrology forecast based on Bayes theory[J].Hydrology，2001，21（5）：33-34.（in Chinese）） DOI：10.3969/ j.issn.1000-0852.2001.05.009.

[7]邢貞相，芮孝芳，劉方貴，等.Nash模型參數不確定性分析及概率洪水預報[J].遼寧工程技術大學學報，2010，29（1）：147-150.（XING Z X，RUI C F，LIU F G，et al.Parameter uncertainty analysis on Nash model and Bayesian probabilistic flood forecasting[J].Journal of Liaoning Technical University （Natural Science Edition），2010，29（1）：147-150.（in Chinese）） DOI：10.3969/ j.issn.1008-0562.2010.01.038.

[8]韓焱紅，矯梅燕，陳靜，等.基于貝葉斯理論的集合降水概率預報方法研究[J].氣象，2013，39（1）：1-10.（HAN Y H，JIAO M Y，CHEN J，et al.Study on the method of rainfall ensemble probability forecast based on bayesian theory and its preliminary experiments[J].Meteorological Monthly，2013，39（1）：1-10.（in Chinese）） DOI：10.7519/ j.issn.1000-0526.2013.01.001.

[9]蔣曉蕾，梁忠民，王春青，等.BFS-HUP 模型在潼關站洪水概率預報中的應用[J].人民黃河，2015，37（7）：13-15.（JIANG X L，LIANG Z M，WANG C Q，et al.Application of BFS-HUP model to flood probabilistic forecasting of Tongguan station[J].Yellow River，2015，37（7）：13-15.（in Chinese）） DOI：10.3969/ j.issn.1000-1379.2015.07.004.

[10][ZK（#]邢貞相.確定性水文模型的貝葉斯概率預報：理論與方法[M].北京：科學出版社，2015.（XING Z X.Bayesian probabilistic prediction for deterministic hydrological models：theory and method[M].Beijing：Science Press，2015.（in Chinese））

[11]KRZYSZTOFOWICZ R，KELLY K S.Hydrologic uncertainty processor for probabilistic river stage forecasting[J].Water Resources Research.2001，36（11）：3265-3277.DOI：10.1029/ 2000WR900108.

[12]KRZYSZTOFOWICZ R.Bayesian theory of probabilistic forecasting via deterministic hydrologic model[J].Water Resources Research，1999，35（9）：2739-2750.10.DOI：1029/ 1999WR900099.

[13]梁忠民，戴榮，王軍，等.基于貝葉斯模型平均理論的水文模型合成預報研究[J].水力發電學報，2010，29（2）：114-118.（LIANG Z M，DAI R，WANG J，et al.Study on forecast combination of different hydrological models by Bayesian model averaging[J].Journal of Hydroelectric Engineering，2010，29（2）：114-118.（in Chinese））

[14]RAFTERY A E，GNEITING T，BALABDAOUI F，et al.Using Bayesian model averaging to calibrate forecast ensembles[J].Monthly Weather Review，2017，133（5）：1155-1174.DOI：10.1175/MWR2906.1.

[15]劉攀，郭生練，田向榮，等.基于貝葉斯理論的水文頻率線型選擇與綜合[J].[JP+2]武漢大學學報（工學版），2005，38（5）：36-40.（ LIU P，GUO S L，TIAN X R，et al.Selecting and averaging of flood frequency models based on Bayesian theory[J].Engineering Journal of Wuhan University，2005，38（5）：36-40.（in Chinese）） DOI：10.3969/ j.issn.1671-8844.2005.05.008.

[16]梁忠民，蔣曉蕾，錢名開，等.考慮誤差異分布的洪水概率預報方法研究[J].水力發電學報，2017，36（4）：18-25.（LIANG Z M，JIANG X L，QIAN M K，et al.Probabilistic flood forecasting considering the heterogeneity of error distributions[J].Journal of Hydroelectric Engineering，2017，36（4）：18-25.（in Chinese）） DOI：10.11660/ slfdxb.20170403.

[17]王艷蘭，梁忠民，蔣曉蕾，等.MCP模型在嘉陵江小河壩站洪水概率預報中的應用[J].水力發電，2017，43（10）：31-35.（WANG Y L，LIANG Z M，JIANG X L，et al.Application of MCP model to flood probabilistic forecasting of Xiaoheba station in Jialing river[J].Water Power，2017，43（10）：31-35.（in Chinese）） DOI：10.3969/ j.issn.0559-9342.2017.10.008.

[18]TODINI E.A model conditional processor to assess predictive uncertainty in flood forecasting[J].International Journal of River Basin Management，2008.6（2）：123-137.DOI：10.1080/ 15715124.2008.9635342.

[19]COCCIA G，TODINI E.Recent developments in predictive uncertainty assessment based on the model conditional processor approach[J].Hydrology and Earth System Sciences，2011，15（10）：3253-3274.DOI：10.5194/ hess-15-3253-2011.

[20]TODINI E.From HUP to MCP：Analogies and extended performances[J].Journal of Hydrology，2013，477（1）：33-42.DOI：10.1016/ j.jhydrol.2012.10.037.

[21]SITTNER W T，SCHAUSS C E，MONRO J C.Continuous hydrograph synthesis with an API-type hydrologic model[J].Water Resources Research，1969，5（5）：1007-1022.DOI：10.1029/ WR005i005p01007.

[22]趙人俊.流域水文模擬[M].北京：水利電力出版社，1984.（ZHAO R J.Hydrological simulation of basin[M].Beijing：Water Resources and Electric Power Press，1984.（in Chinese））

[23]包為民.水文預報-第4版[M].北京：中國水利水電出版社，2009.（BAO W M.Hydrologic forecasting-Fourth Edition[M].Beijing：China Water&Power Press，2009.（in Chinese））

[24]KOENKER R，BASSETT G W.Regression quantiles[J].Econometrica，1978，46：33-50.DOI：10.2307/ 1913643.

[25]XIONG L H， WAN M， WEI X J， et al.Indices for assessing the prediction bounds of hydrological models and application by generalized likelihood uncertainty estimation[J].Hydrological Science Journal， 2009， 54（5）： 852-871.DOI：10.1623/ hysj.54.5.852.