基于滑模控制的四旋翼無人機姿態跟蹤研究
楊永強


摘 要:由于應用廣泛,四旋翼無人機近年來得到了眾多科研人員的關注。本文首先利用Newton-Euler法建立了四旋翼無人機六自由度運動學和動力學模型,并在此基礎上設計了基于反步法、滑模控制和動態面理論的姿態跟蹤控制器:實際姿態與期望姿態間誤差作為控制器輸出,無人機所受合力與各方向力矩作為控制器輸出。最后,通過Matlab對無人機控制系統進行數值仿真,仿真結果表明了所設計姿態控制器的可行性和有效性。
關鍵詞:四旋翼無人機;反步法;滑模控制;姿態跟蹤
中圖分類號:V249 文獻標志碼:A
0 引言
由于具有成本低、使用靈活、體積小等優點,無人機在軍事和民用領域均有廣泛的應用。依據平臺構型,無人機可分為固定翼式、旋翼式和撲翼式等。而在旋翼式無人機中,四旋翼無人機以其結構簡單、使用靈活、易于起降等優點,成為近年來旋翼式無人機研究中的熱點。但是,由于四旋翼無人機體積較小、飛行靈活、周邊流場具有非定常性,因此其控制模型具有較大不確定性,且易受突風干擾。此類未建模動態與外界強擾動對四旋翼無人機控制系統提出了更高的要求,因此如何建立具有強魯棒性的飛行控制系統是四旋翼無人機的關鍵技術之一。
目前對四旋翼無人機飛控系統的研究主要集中于動力學建模和控制器設計等方面。飛控計算機通過獲取當前無人機狀態計算分布于旋翼支架端部的4個電機所需轉速,并對其進行控制。由于無人機獨立執行機構少于其系統自由度,因此四旋翼無人機為欠驅動系統。故四旋翼無人機具有較強的非線性特征且各通道間耦合性強,受擾動影響大,因此難以建立精確,可靠的數學模型。基于其上述特征,四旋翼無人機控制器設計多采用無模型控制和線性控制等方法。近年來,有研究人員將動態逆技術、反步法、智能控制技術等非線性設計方法引入四旋翼無人機控制領域,得到了較好的仿真結果,但上述方法均需較為精確的非線性數學模型,且在線計算量較大,均不具有較高的實用性。
本文利用Newton-Euler法對四旋翼無人機建立較為精確的數學模型,并基于該模型與滑模控制技術、反步法與動態面等方法設計了姿態跟蹤控制律。通過反步法設計內環姿態跟蹤控制律跟蹤期望姿態;通過動態面技術消除反步法設計過程中出現的微分爆炸現象;通過滑模控制消除跟蹤誤差。此外,本文利用Matlab進行了數值仿真,驗證了上述模型的可靠性與控制器的可行性。
1 四旋翼無人機建模
四旋翼無人機機身由4個剛性桿件、固定結構和吊艙支架等部分組成,在桿件末端固連4個獨立電機螺旋槳作為動力系統,提供飛行所需動力。4個獨立電機由飛控系統輸出控制信號單獨驅動,通過差動產生俯仰、滾轉和偏航所需力矩。因此,對于四旋翼無人機運動模型而言,控制輸入為電機螺旋槳的轉速,輸出為無人機的姿態和位置。
1.1 基本假設
為能在反映飛艇運動特性的前提下,盡可能地簡化建模的復雜性,四旋翼無人機運動學與動力學模型的建立,采用以下基本假設:(1)忽略地球曲率和自轉,視地面坐標系為慣性系;(2)無人機機體視為剛體,忽略其微小形變;(3)無人機結構完全對稱;(4)忽略旋翼間相互干擾。
1.2 坐標系定義
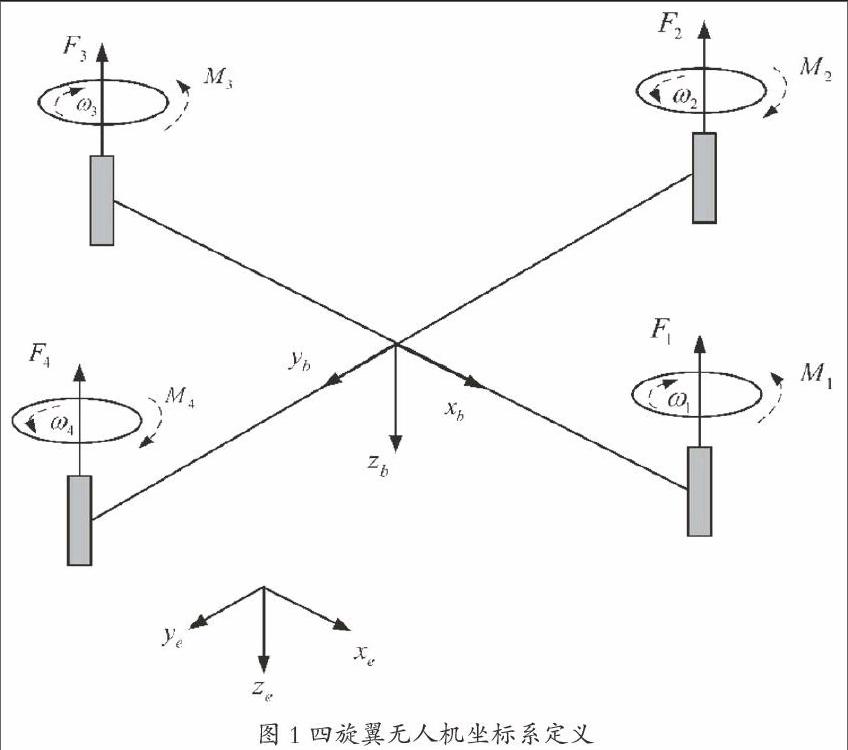
如圖1所示,分別建立地面坐標系和機體坐標系如下:
(1)地面坐標系{Oe xe ye ze}:該坐標系與地面固連。原點Oe 為地面一固定點;Oe xe軸為沿水平面正東方向;Oe ze軸豎直向下;Oe ye軸位于水平面內垂直于Oe xe軸,并與Oe xe軸、Oe ze軸構成右手坐標系。
(1)機體坐標系Ob xb yb zb:該坐標系與機體固連。原點Ob固連于機體中心;Ob xb軸有機體中心指向螺旋槳電機1;Ob zb軸豎直向下;Ob yb軸位于水平面內垂直于Ob xb軸,并與Ob xb軸、Ob zb軸構成右手坐標系。
1.3 數學模型
1.3.1 運動學模型
根據Newton-Euler方程并結合相應的運動學方程,四旋翼無人機的整個運動可由如下方程完全描述:
3 數值仿真
利用Matlab對上述所設計控制系統進行仿真,設定初始姿態角和期望姿態角分別為,。系統所用模型為第二節所建立運動模型,仿真結果如圖2~圖4所示。其中,圖1為仿真過程中姿態角的時間歷程圖;圖2為仿真過程中姿態角速度的時間歷程圖;圖3為仿真過程中控制量的時間歷程圖。分析上述仿真結果可得,四旋翼無人機在較短時間內跟蹤至期望姿態角,并持續收斂;且在運動過程中,無人機控制系統各輸入量在實際約束范圍內。
結論
本文研究了四旋翼無人機的姿態控制問題,首先利用Newton-Euler法對四旋翼無人機建立了六自由度數學模型,并基于李雅普諾夫穩定性理論與滑模控制理論采用反步法設計了姿態跟蹤控制律。此外,引入了動態面技術消除反步法設計過程中出現的微分爆炸現象。最后,本文利用Matlab進行了數值仿真,驗證了上述模型的可靠性與控制器的可行性。本文后續將引入空間制導律,實現四旋翼無人機對控制路徑的跟蹤控制。
參考文獻
[1]廖衛中,宗群,馬亞麗.小型四旋翼無人機建模與有限時間控制[J].控制理論與應用,2015,32(10):1343-1350.
[2]方旭,劉金琨.四旋翼無人機三維航跡規劃及跟蹤控制[J].控制理論與應用,2015,32(8):1120-1128.
[3]尤元,李聞先.四旋翼無人機設計與滑模控制仿真[J].現代電子技術, 2015(15):80-83.
[4] Zheng Z, Chen T, Xu M, et al. Modeling and path-following control of a vector-driven stratospheric satellite[J]. Advances in Space Research, 2016, 57(9):1901-1913.

