考慮包辛格效應的輥式矯直截面反彎特性

馬曉彬，張杰，李洪波，周一中，胡偉東，張中偉

?

考慮包辛格效應的輥式矯直截面反彎特性

馬曉彬1，張杰1，李洪波1，周一中2，胡偉東2，張中偉2

(1. 北京科技大學機械工程學院，北京，100083；2. 寶鋼股份武漢鋼鐵有限公司，湖北武漢，430083)

基于彈塑性彎曲基本原理，以板材進入矯直機后經歷的第2次彎曲為例，建立考慮包辛格效應影響程度(Ba)的輥式矯直復雜彎曲力學模型。采用該模型計算Ba對第2次彎曲時?關系和?關系及殘余應力的影響，證明輥式矯直過程中經歷多次彈塑性彎曲的截面反彎特性受材料包辛格效應的影響，而且隨著材料強化系數的增大，截面彎曲特性所受影響越顯著。最后計算相同矯直工況下，Ba不同的材料的殘余曲率，得到材料Ba對于殘余曲率的影響。研究結果表明：強化系數較大(＞0.01)的材料進行矯直仿真時應考慮包辛格效應，在實際生產中確定工藝參數時需要首先確定材料的Ba。

包辛格效應；輥式矯直；強化系數；彎矩?曲率；殘余應力

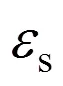
1 材料性質與參數設定

1.1 包辛格效應及其強化模型

當強化材料正向加載到一定程度的塑性應變后，此時的應力稱為正向后繼屈服應力，它是材料卸載并重新正向加載時新的屈服應力；但是在卸載并按反向施加載荷后，其反向后繼屈服應力的絕對值要比正向屈服應力下降，這種現象稱為包辛格效應。描述材料在塑性加載—卸載—再加載過程中的應力應變關系的強化模型主要分為3類：各向同性強化、隨動強化和混合強化。當強化材料的應力應變關系采用如式(1)所示的雙線性強化模型描述，3種強化模型所描述的材料單向循環拉壓時的單軸應力應變關系存在較大差別，如圖1所示。

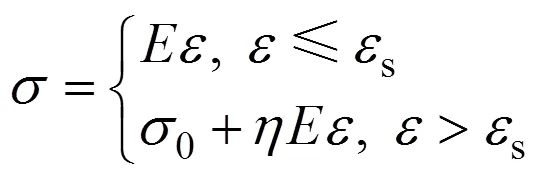
式中：為應力；E為材料的彈性模量；為應變；為屈服應變；為截距應力，等于；η為材料的強化系數，等于塑性段直線斜率。

從圖1可以看出：各向同性強化不能體現包辛格效應，隨動強化模型只能描述一種包辛格效應影響程度，而一般材料在復雜加載路徑下不單純表現為各向同性強化和隨動強化，而是介于2種強化模型之間，是兩者的結合，稱為混合強化模型。

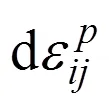
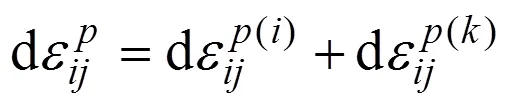
由此可以得到正向加載后，反向后繼屈服應力為

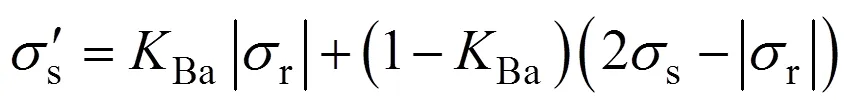
1.2 彎曲參數設定

利用彈塑性彎曲理論[14]對輥式矯直過程進行分析，為了簡化分析過程，對彎曲過程中相關參數進行量綱一化。設矩形截面高度為，彈性極限彎矩為t，彈性極限曲率角為t。彎曲時，截面彈性區高度為t，截面彎矩為，彎曲曲率角為。以這些參數為基礎，進行如下定義：

2) 彈區比為=t/，反映截面塑性變形程度；

3) 曲率比為=/t=1/，即彎曲過程中各種曲率角對彈性極限曲率角的比值，反映截面彎曲程度；

4) 相對高度為=/，取值范圍是[?1，1]，反映研究點的相對位置。

2 考慮包辛格效應的反復彎曲分析

金屬板帶材在輥式矯直過程中經歷的連續多次彈塑性彎曲可以分為簡單彈塑性彎曲和復雜彈塑性彎曲。當完全不考慮(或不存在)彎曲截面的殘余應力時，即為簡單彈塑性彎曲，例如輥式矯直的第1次彎曲過程；在簡單彈塑性彎曲基礎上，再經過1次或多次彈塑性彎曲，即為復雜彈塑性彎曲，輥式矯直第2次及之后的彎曲就屬于此列。以受包辛格效應影響的強化材料的輥式矯直過程中前2次彎曲為例，分析這2類彎曲過程中的截面應力分布、彎曲力矩、卸載后的應力分布和后繼屈服應力分布等參數，確定2種情況下包辛格效應對截面彎曲特性的影響。

2.1 強化材料的簡單彈塑性彎曲

崔甫等[1, 8]研究了強化材料簡單彈塑性彎曲過程中的應力演化過程。設材料屈服應力為s，強化系數為，截面彎曲曲率比為，則彎曲過程中沿高度方向加載應力分布方程為

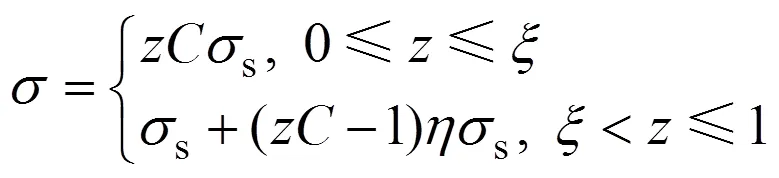
彎矩與曲率比的關系(即?關系)為

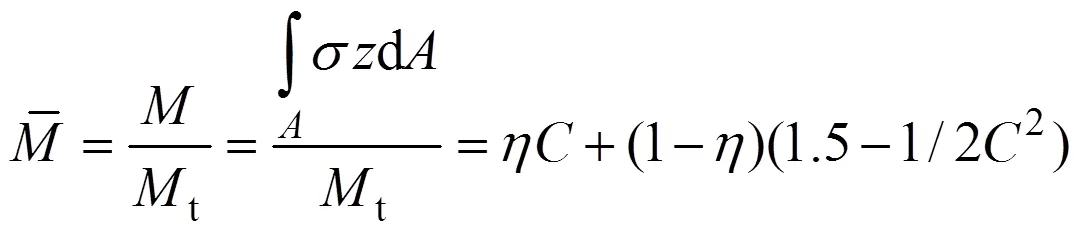
卸載后截面殘余應力分布方程為

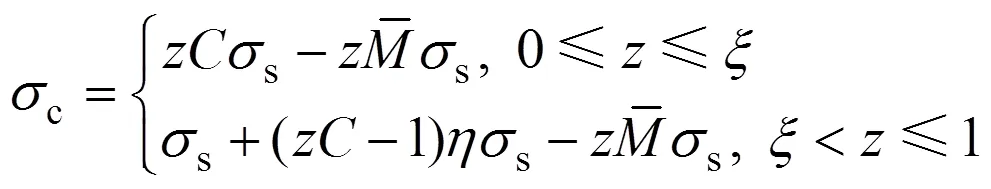
強化材料在簡單彈塑性彎曲過程中截面應力演變過程如圖2(a)和2(b)所示。由圖2可知：截面應力分布的對稱關系，因此，式(4)和式(6)中只列出了[0，1]區間的應力分布，[?1，0]區間的應力分布可由對稱關系求得，文后列舉的公式依照此方法。

強化材料截面在簡單彈塑性彎曲過程中截面表層部分進入后繼屈服過程，材料的包辛格效應導致板材截面表層在彎曲加載過程中后繼屈服應力改變。板材截面加載方向的后繼屈服應力由彎曲加載的最大應力確定；反方向的后繼屈服應力則隨Ba不同而變動，如圖2(c)所示。圖2(c)中陰影區即為由Ba決定的反方向后繼屈服應力范圍。

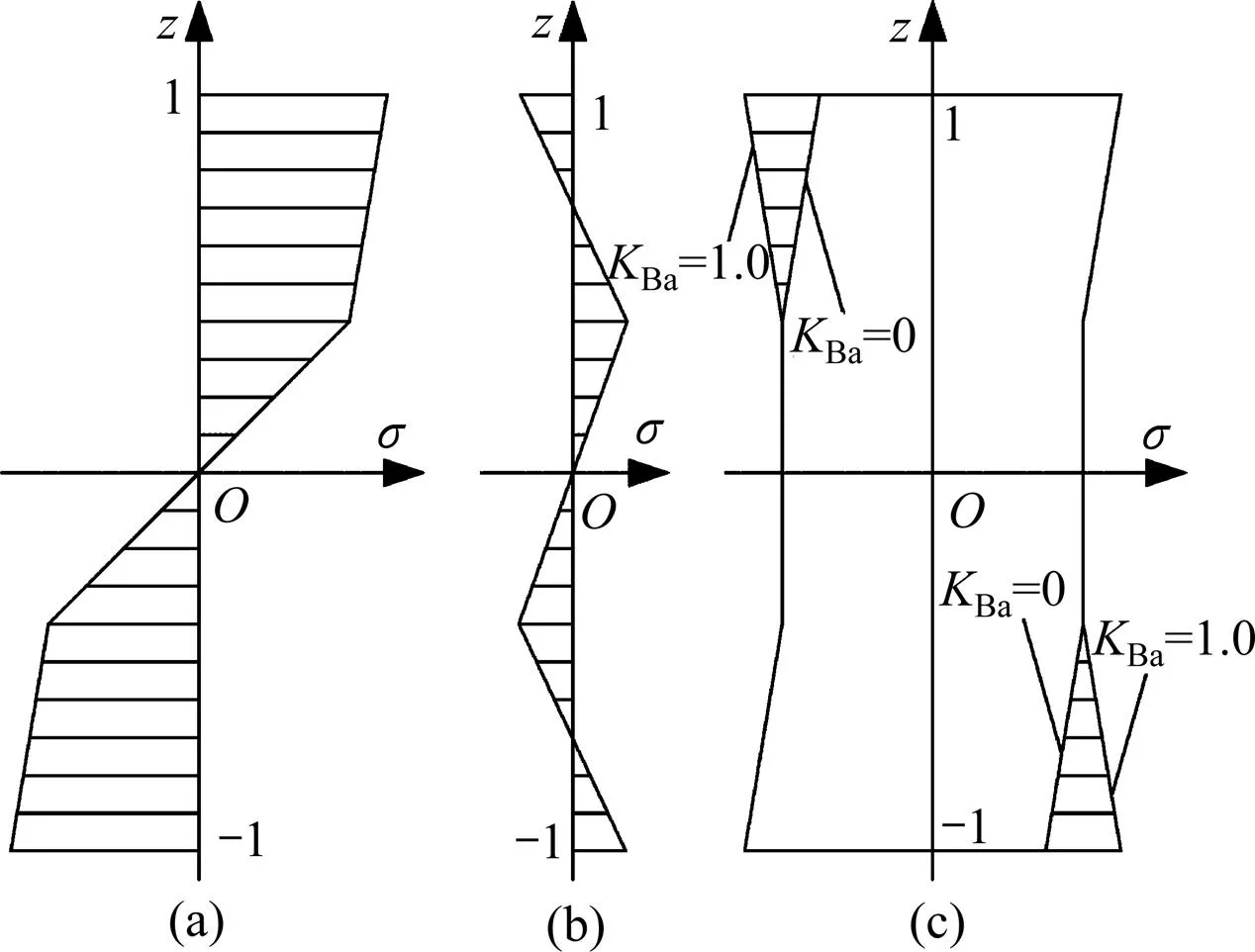
(a) 加載應力；(b) 殘余應力；(c) 后繼屈服應力

板材截面后繼屈服應力的改變，導致強化材料截面在后續彎曲加載過程中，截面不同高度處的進入屈服所需的應力發生改變，從而影響后一次彎曲過程中的?關系。

2.2 強化材料的第2次彈塑性彎曲

強化材料第2次彈塑性彎曲是復雜彈塑性彎曲中力學模型最簡單的一種，通過對第2次彈塑性彎曲的推導，可以得到分析更高次復雜彈塑性彎曲的截面彎曲特性的基本原理與方法。設截面第1次正方向彎曲曲率比為1，第2次反向彎曲曲率比為2，分析強化材料的第2次彈塑性彎曲過程。

2.2.1 應力分布與彎矩

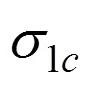
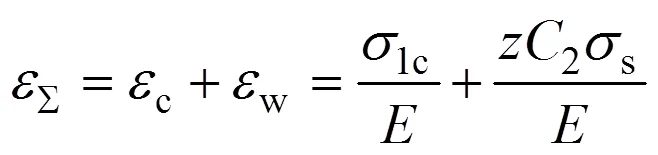
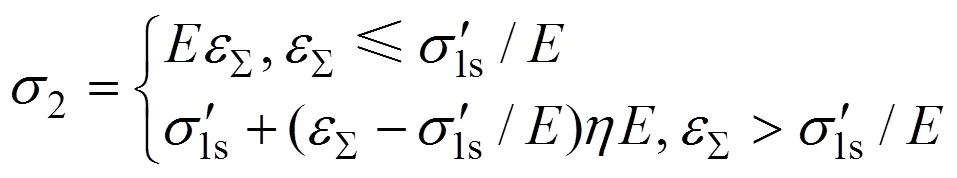
結合式(7)和式(8)可知：第2次彎曲加載的應力分布可以根據2的大小分成3種不同的形式，如圖3 所示。

1—殘余應力；2—彈性極限應力分布；3—Ⅰ型與Ⅱ型應力分布邊界；4—后繼屈服應力；5—Ⅰ型彈塑性應力分布；6—Ⅱ型彈塑性應力分布。

圖3 第2次彎曲加載前后的應力分布

Fig. 3 Distribution of section stress before and after loading step of the second bending process

3種不同的應力分布方程及該情況下彎曲加載的彎矩方程如下。

1) 彈性應力分布。此時矩形板材截面各高度處尚未進入塑性變形階段，將式(6)和式(7)代入式(8)可得該情況下的加載應力分布方程為

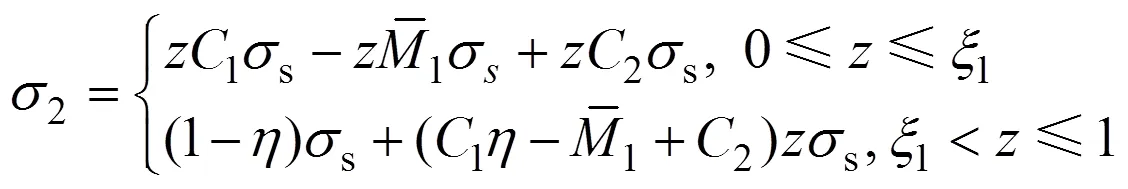
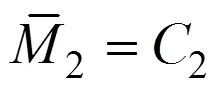
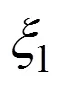
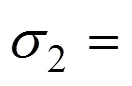
將截面應力對截面形心取矩，得到Ⅰ型應力分布時的彎矩比：

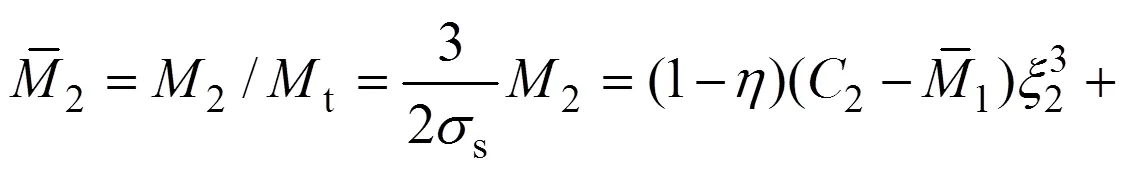
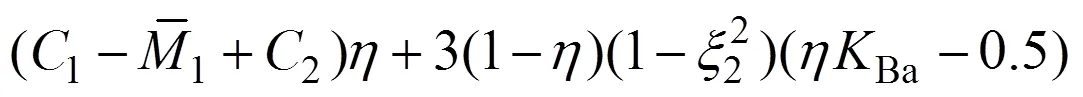
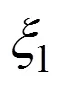
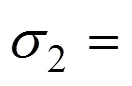
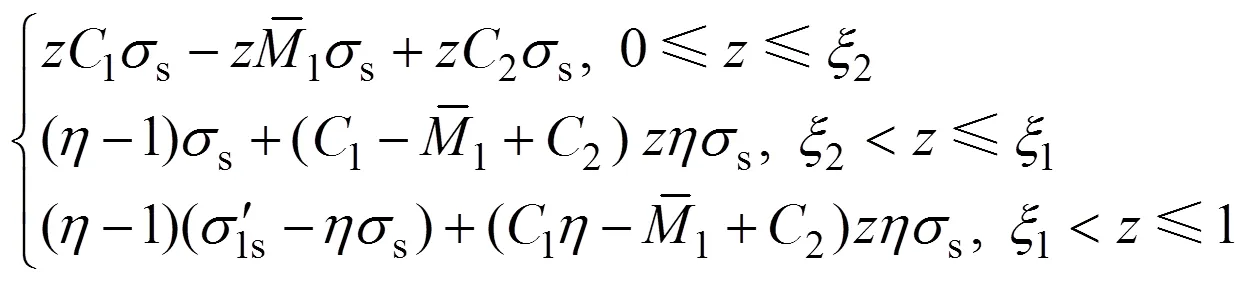
此時的彎矩比為

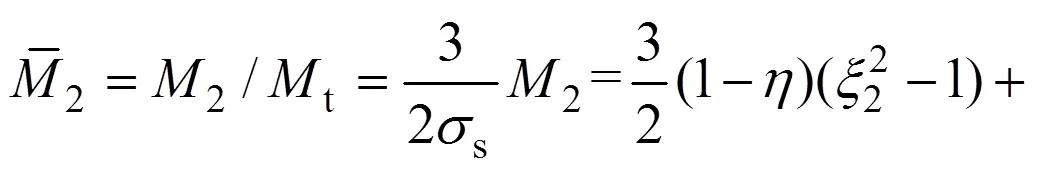
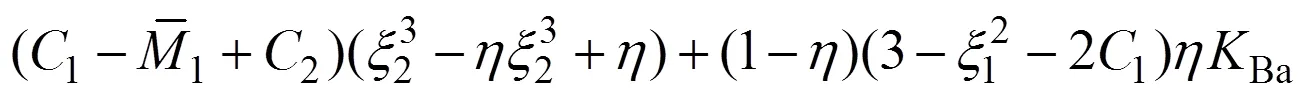
2.2.2 應力分布邊界

由前面的推導可以看出：第2次彎曲加載后的應力分布形式以及對應的彎矩比、彈區比等均與第1次彎曲時不同，明晰第2次彎曲加載后3種應力分布的邊界，確定第2次彎曲加載時的?關系，是分析包辛格效應對第2次彎曲加載影響的前提。

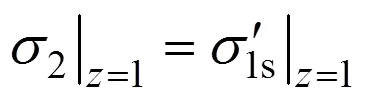
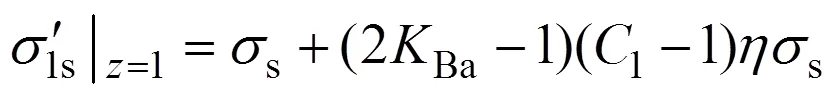
聯立式(9)和式(15)，整理可得彈性極限邊界方程為

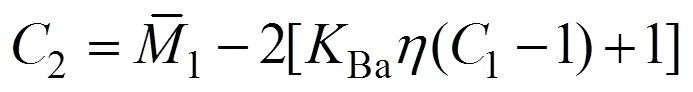
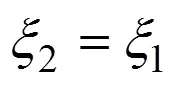
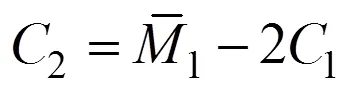
式(16)和式(17)所描述的邊界將空間分割為3個區域，分別是彈性彎曲區、Ⅰ型應力分布區與Ⅱ型應力分布區，兩邊界如圖4所示。

2.2.3 殘余應力與后繼屈服應力

根據彈塑性彎曲的彈性回復理論，彈性卸載的力矩與彎曲力矩相等，方向相反，則最終的殘余應力分布為

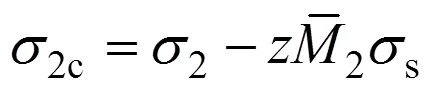
由于彈性加載階段的加載應力與彈復應力相等，因此，第2次彈性加載的殘余應力分布與未加載前的應力分布相同。對于Ⅰ型與Ⅱ型加載，結合式(11)~(14)和式(18)，就可以計算出2種情況下的殘余應力分布函數，得到殘余應力分布曲線，如圖5所示。第2次彎曲卸載后的截面后繼屈服應力可由加載應力分布和式(3)共同確定。

1—Ⅰ型彈塑性應力分布；2—Ⅱ型彈塑性應力分布。

圖5 第2次彎曲卸載后的殘余應力

Fig. 5 Distribution of section residual stress after unloading step of the second bending process

3 包辛格效應對2次彎曲的影響

通過之前的推導，得到了第2次彎曲的加載應力分布形式，卸載后殘余應力和后繼屈服應力以及加載所需的彎矩。現通過上述方程分析第2次彎曲時Ba對截面彎曲特性的影響，以及，1和2等參數的變化引起Ba的改變。

3.1 加載過程

彎曲加載時截面彈區比與彎曲曲率比的關系(?關系)和彎矩比方程(?關系)反映了該截面的彎曲特性。在矯直仿真計算中，?關系、?關系是否準確，決定了計算出的矯直機壓下參數在實際生產應用中的效果。根據前面對第2次彎曲過程分析，由式(12)和式(16)得到Ba對彈區比和彈性極限曲率的影響，如圖6所示。

從圖6(a)可以看出：相同條件下，Ba不同時彈區比也不相同，而且在高強化系數、低彎曲曲率比的情況下，Ba不同引起的彈區比差別更大，如2=1且強化系數較大(=0.05)時2相差17.03%，而強化系數較小(=0.01)時僅相差2.87%。同樣從圖6(b)也可以看到：強化系數越高，Ba引起的彈性極限曲率比差值越顯著，當增加到0.05時，不同Ba下的彈性極限曲率比差值可達43.08%，即使=0.01，差值也有16.50%。由以上分析可以看出：材料的包辛格效應影響程度不同，第2次彎曲時?關系和彈性極限曲率也會隨之改變，當材料強化系數較高且第2次彎曲曲率比較小時，Ba對?關系和彈性極限曲率的影響越大。

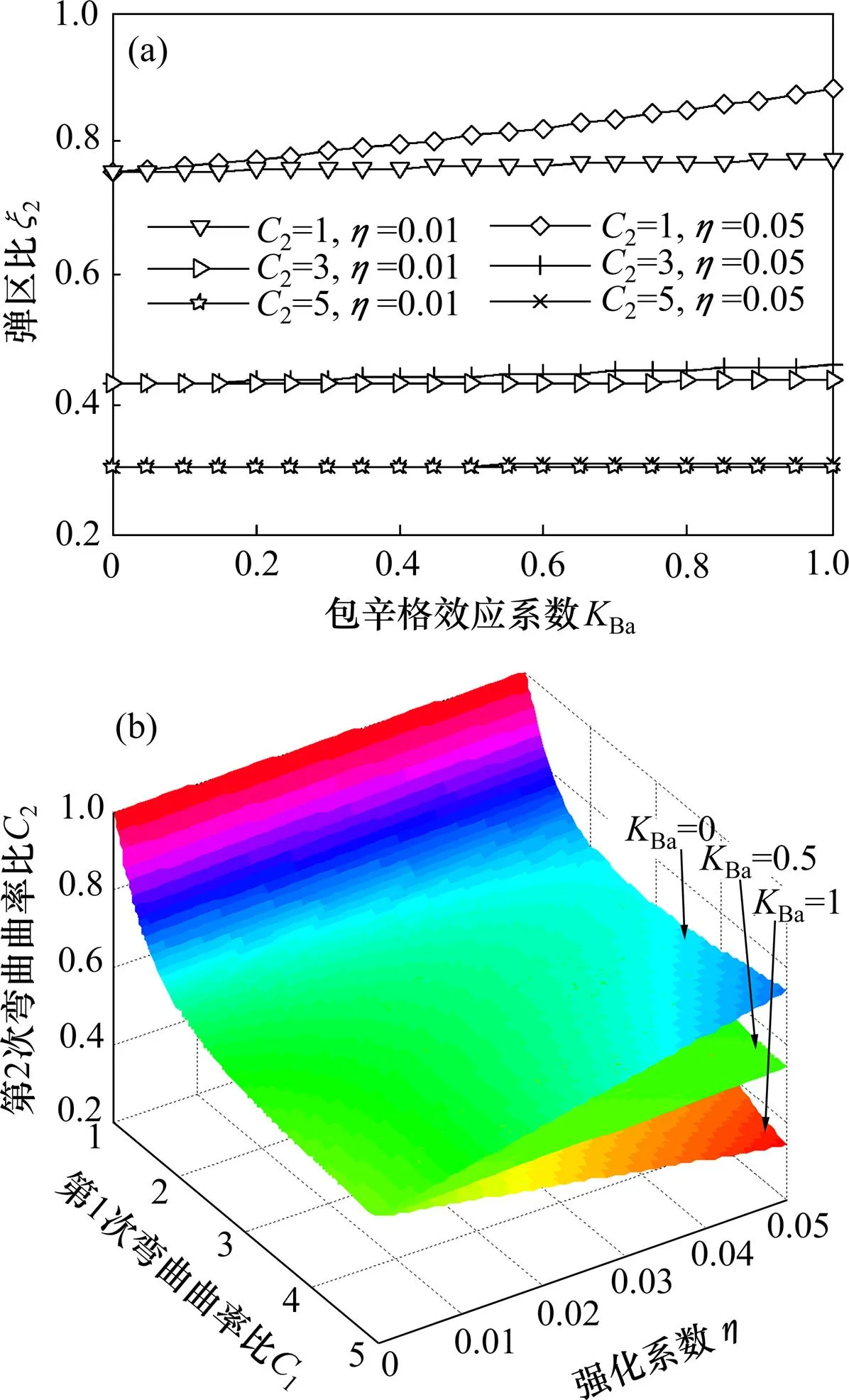
(a) KBa對彈區比的影響；(b) KBa對彈性極限曲率比的影響

由式(12)和式(14)可以得到不同情況下Ba對第2次彎曲過程中?關系的影響，如圖7所示。

由圖7可知：1和越大，Ba的變化引起的第2次彎曲過程中?關系的變化越顯著，如1=5，=0.05時，2在(1，5)區間內的第2次彎曲彎矩比平均差值達到24.92%，最大差值達到26.52%。

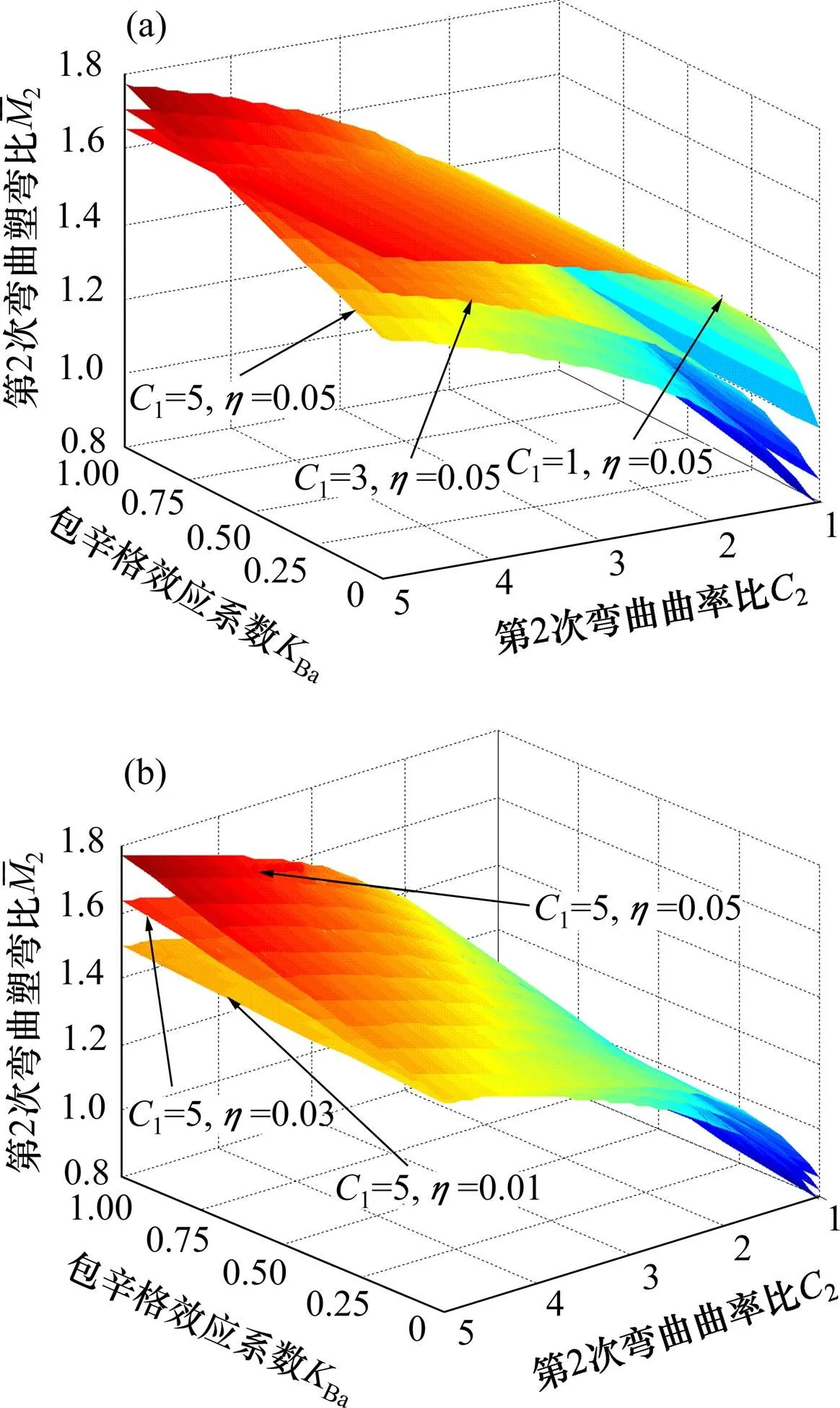
(a) C1不同，η相同時；(b) C1不同，η不同時

由以上分析可以看出：在材料屬性和彎曲參數確定的情況下，第2次彎曲的截面更易于進入塑性變形；在大強化系數、小彎曲曲率比的情況下，Ba變化引起2的變化量更大，由于矯直機出口段矯直輥壓下量小，對板材施加的彎曲曲率比小，Ba不同的材料經過矯直后的殘余應力分布會發生顯著改變。第2次彎曲時相同的曲率比所需要的彎矩相對簡單彎曲時更小，這意味著第2次彎曲的彈復應力更小，因此，在實際輥式矯直過程中，不能只根據經典矯直理論設定矯直參數，要充分考慮2次及更高次彎曲時?關系的改變以及其對彈復后殘余曲率的影響，即要達到同樣的殘余曲率要求，相較于經典理論應減小彎矩，即在實際生產中適當減小壓下量。

3.2 卸載過程

彎曲卸載時主要關注截面內剩余的殘余應力的分布情況及其大小，根據2.2.3節所述的第2次彎曲卸載殘余應力計算方法，設s=500 MPa，=0.05，1=3，2和Ba分別取不同的值，計算第2次彎曲的殘余 應力。

圖8所示為Ⅰ型與Ⅱ型2種應力分布的情況下卸載后的殘余應力。從圖8可知：在相同條件下，Ba變化引起的殘余應力分布形式和峰值的變化很小，最大峰值應力差僅為12.33%(2=3時)；而最大表層應力差出現在2=1時，相對差值為158.02%，表明2較小時Ba的影響更大。在2逐漸增加的過程中，殘余應力峰值有一個先減小后增加的過程，這要求在輥式過程中需要合適的壓彎量以實現較小的殘余應力。

當其他彎曲參數相同，=0.01的材料第2次彎曲的殘余應力峰值對于Ba的變化更加不敏感，最大峰值應力差僅為2.12%(2=3時)；而最大表層應力差為21.66%(2=1時)。

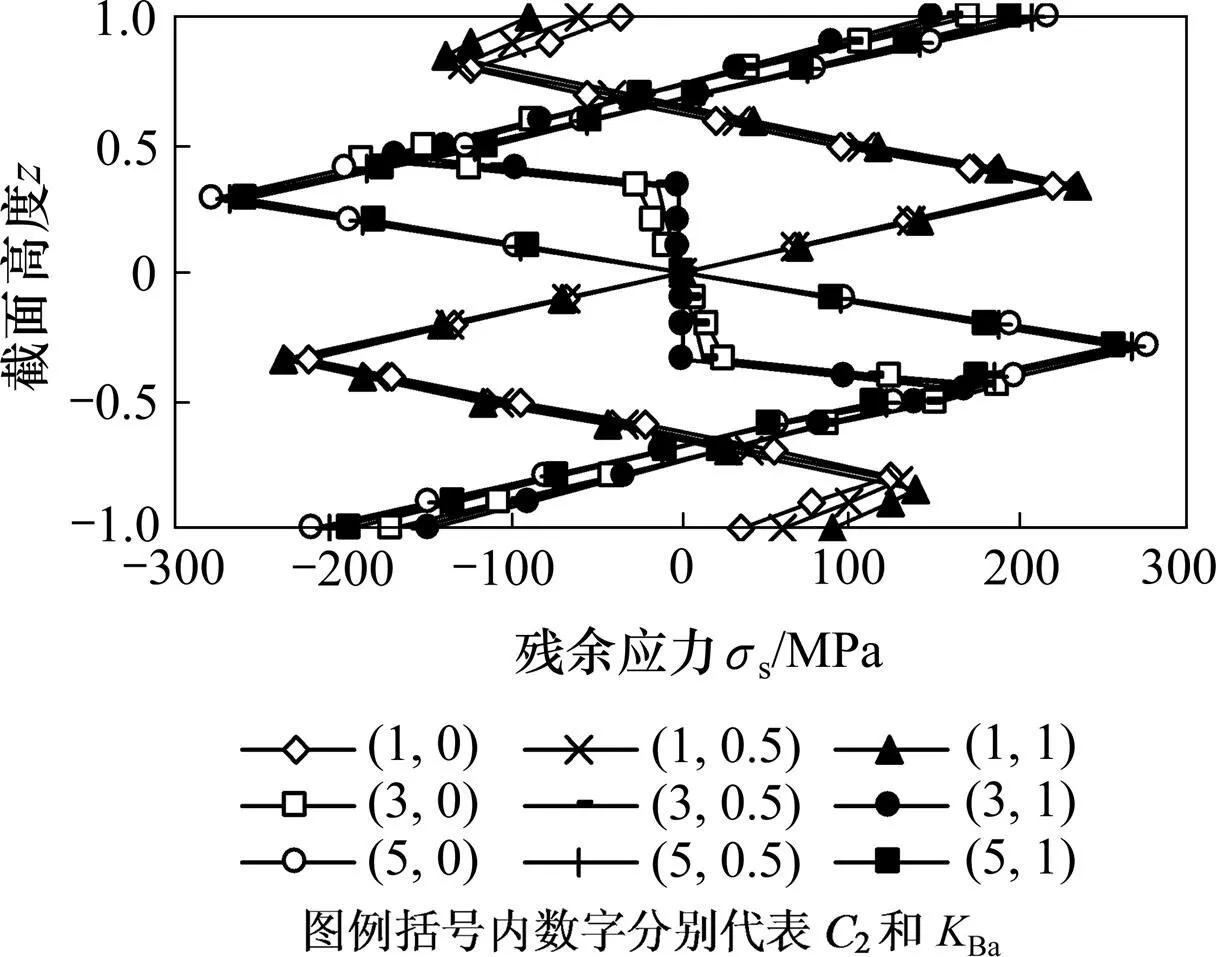
圖8 KBa對第2次彎曲殘余應力的影響

4 包辛格效應對高次彎曲的影響

在實際的輥式矯直過程中，金屬板材各截面最終要經歷3次以上的彈塑性連續彎曲過程。參考以上對2次反彎的彈塑性解析可知：隨著截面上彎曲次數的增加，截面應力分布方程和后繼屈服應力愈加復雜。采用解析的方法求解較為困難，根據上述第2次反彎過程的分析流程，采用合理的數值計算方法可以更加簡單、快捷地解決問題。

板材的截面反彎特性在經歷彈塑性彎曲之后，由于包辛格效應的影響而產生改變，為了分析截面反彎特性的改變對板材矯直過程的影響，總結不同Ba的板材經歷相同的彎曲歷史后的殘余曲率，以某11輥矯直機為例，根據前述彈塑性彎曲分析過程，以數值計算的方法進行分析。設矩形金屬板材最大截面初始曲率0max=±3.0(使鋼板凹向下的彎曲為正)，各截面初始曲率在該板材上隨機連續分布；0.2=724.09 MPa，=194.7 GPa，=0.013 4。設定3組基于大應變原則的整體傾斜壓下彎曲工藝參數w如表1所示。矯直機入口和出口處的第1輥和第11輥處的彎曲曲率均 為0。

表1 第i輥處的設定彎曲曲率Cwi

卸載后的截面殘余應力、殘余曲率和后繼屈服應力作為初始狀態，結合該次彎曲曲率wi就可以計算該次彎曲后的截面應力分布，從而得到彎曲力矩，進而計算出殘余曲率、殘余應力和后繼屈服應力等參數。依照該流程，逐道次計算，即可得到材料Ba對于矯直出口殘余曲率的影響，如圖9所示。

圖9所示為在不同的壓下方案中，材料Ba不同時對其矯直出口殘余應力的影響。從圖9可知：增加矯直過程中的w可以有效降低板材的出口殘余曲率，但是，隨著w增大，增加w產生的出口殘余曲率減小的效果逐漸下降；在Ba由0增加到1的過程中，出口殘余曲率有一個先減小而后平穩最后減小的過程，Ba處于[0,0.2]和[0.9,1]這2個區間時，板材的出口殘余曲率受到Ba的很大影響，因此，在矯直生產中，需要首先確定板材受到的包辛格效應，并據此設定合理的矯直工藝參數，以獲得板形質量合格的板材。

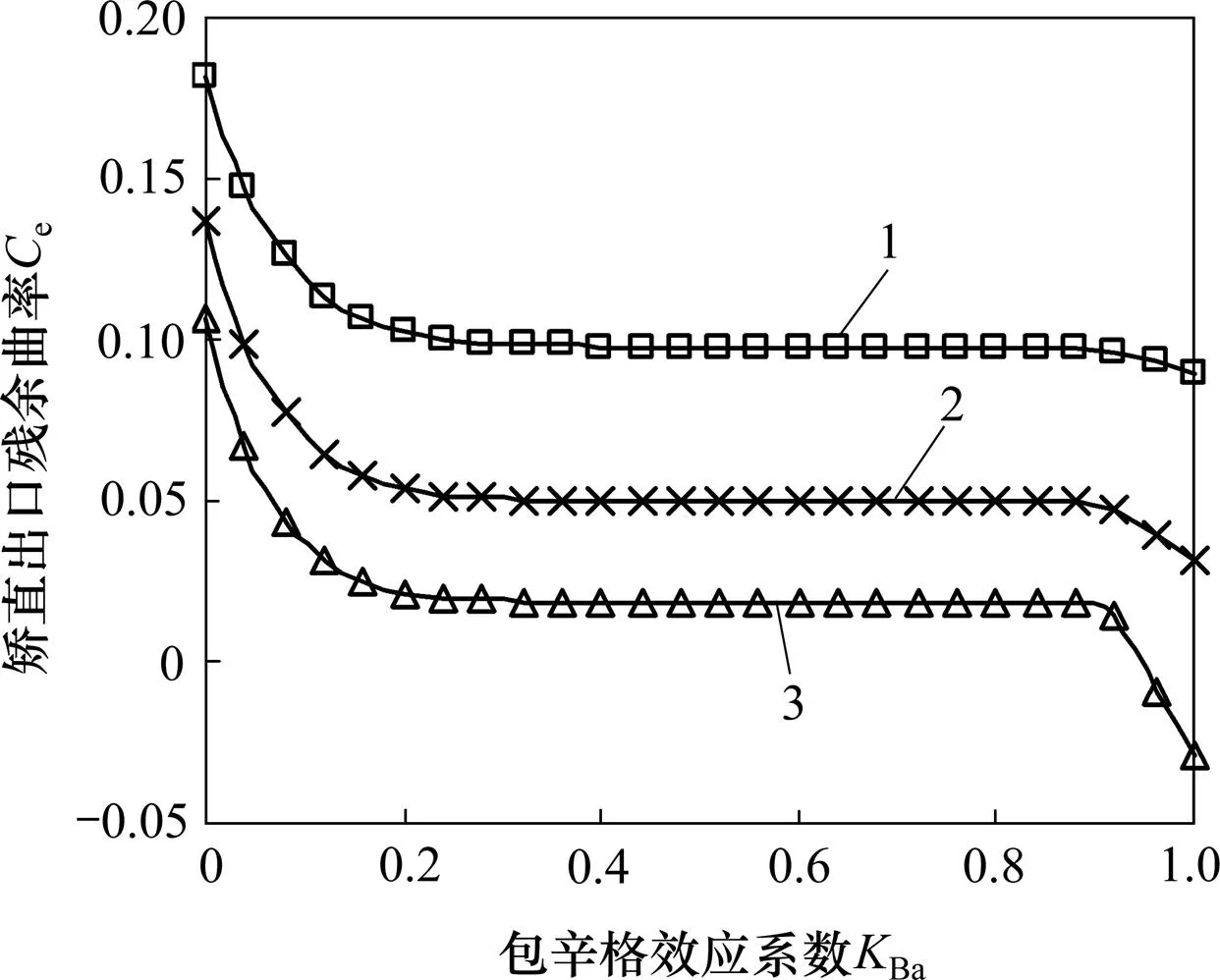
1—工藝參數1；2—工藝參數2；3—工藝參數3。

5 結論

1) 考慮材料的包辛格效應，重點分析了強化材料板材在矯直過程中的第2次彎曲過程，得到了彎曲過程中截面加載應力分布、殘余應力分布、后繼屈服應力分布、?關系和?關系等關于Ba的方程。

2)Ba不同的強化材料在彎曲過程中的?關系和?關系也不相同，材料的強化系數以及彎曲加載歷史都會改變Ba變化所產生的影響。

3) 第2次彎曲產生的殘余應力的峰值受Ba影響較小，表層殘余應力在第2次彎曲曲率比較小時受Ba改變的影響較大，較大的強化系數會增強Ba改變時對殘余應力的影響。

4) 強化系數較大(＞0.01)的強化材料采用輥式矯直方式矯直時，材料的Ba不同導致最終矯直出口殘余曲率不同，因此，對多次連續反彎的輥式矯直過程進行仿真分析時需要考慮材料的包辛格效應，并采用相應的Ba進行計算。

[1] 崔甫. 矯直原理與矯直機械[M]. 北京: 冶金工業出版社, 2005: 1?60.CUI Fu. Straightening and straightening machine[M]. Beijing：Metallurgical Industry Press, 2005: 1?60.

[2] HAN K, TYNE C J V, LEVY B S. Effect of strain and strain rate on the Bauschinger effect response of three different steels[J]. Metallurgical and Materials Transactions A, 2005, 36(9): 2379?2384.

[3] CHEN Min, JIANG Xiaomin, ZHAO Zuxin. Innovation in the computing system of straightening force[J]. Chinese Journal of Mechanical Engineering, 2010, 23(1): 115?121.

[4] SCHLEINZER G, FISCHER F D. Residual stress formation during the roller straightening of railway rails[J]. International Journal of Mechanical Science, 2001, 43(10): 2281?2295.

[5] CHEN Weihua, LIU Juan, Cui Zhenshan, et al. A 2.5-dimensional analytical model of cold leveling for plates with transverse wave defects[J]. Journal of Iron and Steel Research, International, 2015, 22(8): 664?671.

[6] LIU Zhifang, LUO Yuanxin, YAN Xingchun, et al. Boundary determination of leveling capacity for plate roller leveler based on curvature integration method[J]. Journal of Central South University, 2015, 22(12): 4608?4615.

[7] 管奔, 臧勇, 逄曉男, 等. 矯直過程截面復雜反彎的應力分布與反彎特性解析[J]. 中南大學學報(自然科學版), 2012, 43(5): 1739?1745. GUAN Ben, ZANG Yong, PANG Xiaonan, et al. Stress distribution and reverse bending behavior of section during roller leveling process [J]. Journal of Central South University(Science and Technology), 2012, 43(5): 1739?1745.

[8] 劉東冶, 何安瑞, 王海濱, 等. 塑性強化材料矯直反彎特性研究[J]. 機械工程學報, 2015, 51(8): 76?83. LIU Dongye, HE Anrui, WANG Haibin, et al. Reverse bending research of leveling on plastic hardening material[J]. Journal of Mechanical Engineering, 2015, 51(8): 76?83.

[9] SEO J H, TYNE C J V, MOON Y H. Effect of roll configuration on the leveling effectiveness of tail-up bent plate using finite-element analysis[J]. Journal of Manufacturing Science and Engineering, 2016, 138(7): 071004.1?071004.7.

[10] 楊海波, 汪家才, 王衛平. 重軌矯直過程應力應變模型的確定與分析[J]. 北京科技大學學報, 1997, 19(增刊): 104?108. YANG Haibo, WANG Jiacai, WANG Werping. Determination of relationship between stress and strain and analysis of mechanical property in rail straightening[J]. Journal of University of Science and Technology Beijing, 1997, 19(Suppl): 104?108.

[11] SILVESTRE E, MENDIGUREN J, GALDOS L, et al. Comparison of the hardening behavior of different steel families: from mild and stainless steel to advanced high strength steels[J]. International Journal of Mechanical Science, 2015, 101/102(4): 10?20.

[12] 莊京彪, 劉迪輝, 李光耀. 基于包辛格效應的回彈仿真分析[J]. 機械工程學報, 2013, 49(22): 84?90. ZHUANG Jingbiao, LIU Dihui, LI Guangyao. Analysis of springback simulation based on Bauschinger effect[J]. Journal of Mechanical Engineering, 2013, 49(22): 84?90.

[13] HODGE P G. Discussion of the Prager hardening law[J]. ASME J. Appl. Mech., 1957, 24: 482?484.

[14] 趙軍, 殷璟, 馬瑞, 等. 小曲率平面彎曲彈復方程[J]. 中國科學：技術科學, 2011, 41(10): 1342?1352. ZHAO Jun, YIN Jing, MA Rui, et al. Springback equation of small curvature plane bending[J]. Science China Technological Sciences, 2011, 41(10): 1342?1352.

(編輯 楊幼平)

Reverse bending behavior of section during roller leveling process considering Bauschinger effect

MA Xiaobin1, ZHANG Jie1, LI Hongbo1, ZHOU Yizhong2, HU Weidong2, ZHANG Zhongwei2

(1. School of Mechanical Engineering, University of Science and Technology Beijing, Beijing 100083, China; 2. Baosteel Wuhan Iron & Steel Co. Ltd., Wuhan 430083, China)

Based on the basic theory of elastic-plastic bending, a mechanical model of complicated bending process of the section under different degrees of Bauschinger effect (Ba) was built by taking the second bend of the plate bears after bited into the leveler as an example. The effect ofBaon the?and?relation and residual stress distribution could be gotten through the model calculation, which could prove that the reverse bending behavior of the elastic-plastic bending section, after experiencing several times of deformation during roller leveling process, was affected by the Bauschinger effect of the material. And more pronounced was gotten with the increase of the strength coefficient of the material. Finally, the residual curvatures of materials with differentBaunder the same process conditions were calculated and the effect ofBaon it were gotten. The results show that the Bauschinger effect should be considered when roller leveling with the coefficient of the material is big(＞0.01) andBaof the material needs to be firstly determined when process parameters in actual production are determined.

Bauschinger effect; roller leveling; strength coefficient; moment-curvature; residual stress

TG333.2

A

1672?7207(2018)01?0087?08

10.11817/j.issn.1672-7207.2018.01.012

2016?12?27；

2017?02?29

國家“十二五”科技支撐計劃項目(2015BAF30B01) (Project(2015BAF30B01) supported by the National Key Technology R&D Program of the 12th Five-Year Plan of China)

張杰，博士，教授，從事板帶軋制技術與裝備研究；E-mail: zhangjie@ustb.edu.cn