節點電壓向量法在計量檢定工作中的應用

韓越

摘要：隨著科學技術的發展，各種電學設備日新月異，其計量檢定工作也越來越復雜。計量檢定的精準度直接關系著電學設備的后期使用，本文提出了一種基于節點電壓向量的故障診斷方式，從而實現故障的快速定位。

Abstract： With the development of science and technology， a variety of electrical equipment changes every day. The measurement verification work is becoming more and more complex. The accuracy of measurement verification is directly related to the later use of electrical equipment. In this paper， a fault diagnosis method based on node-voltage vector is proposed to realize fault location rapidly.

關鍵詞：故障診斷；節點電壓向量 ；數據處理；計量檢定

Key words： fault diagnosis；node-voltage vector；data processing；metrological verification

中圖分類號：TH71 文獻標識碼：A 文章編號：1006-4311（2017）35-0207-03

0 引言

目前，我國企業對電學設備的需求越來越大，各種電學設備在人們生產生活中的影響也逐漸增強，為了確保電學設備的正常運行和使用，就要定期對其進行計量檢定。在計量檢定工作中，必然會發現設備的一些故障，在影響檢測結果精確性的同時，也會使設備的后期使用出現相關問題。所以，在計量檢定工作中發現設備故障后，能快速地實現對故障的診斷和定位，顯得非常重要。

1 電學設備的故障分類

電學設備的核心部件是各種電路元件，電路故障類別繁多。按照某一時段故障是否只有一種分為多故障和單故障，單故障的診斷比多故障診斷要簡單很多，但實際上多故障也是由多種單故障組成的，因此很多時候是可以用單故障的診斷方法來處理多故障問題的。依據故障和損壞的嚴重程度可以分為軟故障和硬故障，硬故障通常是元件數值發生偏差情況非常嚴重，結果將造成災難性的的電路系統故障，軟故障則是當電路元件出現老化變質等原因時，其參數數值就會超過容差允許的范圍，從而造成故障的出現。硬故障可以看作是軟故障的某種極限形式，元件出現開路的情況可以看作是軟故障的極大值，出現短路的情況可以看作是極小值[1]。因此，大多數針對系統軟故障的處理方法在硬故障領域也都是適用的。圖1是發生故障時電路性能參數變化圖。

從圖1可以看出，元件參數在標稱值上下浮動10%是正常范圍，大于10倍或小于0.1倍的標稱值時可以認定電路發生硬故障，其余情況可以認為是軟故障。

2 直流激勵下的故障定位

本文主要是研究電路的單、軟故障，為了方便對節點電壓向量提取法的研究，本文以該方法在電路的單、硬故障中的應用為例來說明，如圖2所示為某電學設備內二階RC低通濾波電路[2]。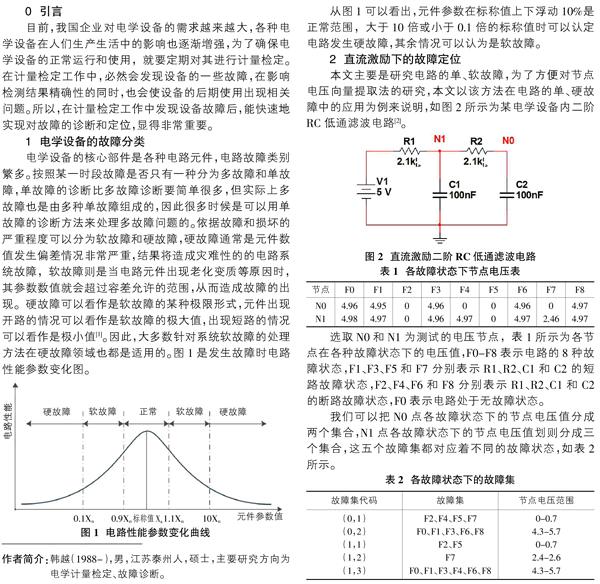

選取N0和N1為測試的電壓節點，表1所示為各節點在各種故障狀態下的電壓值，F0-F8表示電路的8種故障狀態，F1、F3、F5和F7分別表示R1、R2、C1和C2的短路故障狀態，F2、F4、F6和F8分別表示R1、R2、C1和C2的斷路故障狀態，F0表示電路處于無故障狀態。

我們可以把N0點各故障狀態下的節點電壓值分成兩個集合，N1點各故障狀態下的節點電壓值劃則分成三個集合，這五個故障集都對應著不同的故障狀態，如表2所示。

從表3中我們可以很明顯的區分出F4故障（R2斷路）和F7故障（C2短路），但是其他的故障就無法通過這種簡單的方法來確定，因此，故障診斷率僅僅是25%。

3 交流激勵下的故障定位

雖然使用直流激勵來尋找故障集交集的方法簡單易行，但是不能適用于其他多數電路，特別是那些含電容元件的模擬電路[3]。進一步研究，如圖3所示，RC低通濾波電路的激勵源是正弦激勵。

表5中，除了F2和F5故障，其他故障都可以明顯的被診斷出來，可以看出，對電路施加了正弦激勵后，節點電壓值和施加直流激勵時的區別很大。通過對多節點電壓幅值和相角的提取，就可以準確診斷出75%的故障。

4 結束語

節點電壓向量法是直流節點電壓法故障診斷方法的擴展和延伸。在電學計量檢定工作中，如果發現所測數據誤差較大，可以采用此方法進行快速故障定位，方便易行。但是，本方法也存在一定的局限性，在數字電路元件比較多的電學設備中的應用還需要進一步研究。

參考文獻：

[1]朱大奇.電子設備故障診斷原理與實踐[M].電子工業出版社，2004：1-20.

[2]Miche Y， Van Heeswijk M， Bas P， Simula O， Lendassc A. TROP-ELM： A double-regularized ELM using LARS and Tikhonov regularization[J]. Neurocomputing， 2011，74： 2413-2421.

[3]何宏華.電壓電流相序對電能測量影響的研究[J].電子世界，2013（10）：213-215.

[4]張慶輝，崔勇，朱亞峰.基于DSP的諧波電能計量算法研究[J].電測與儀表，2014，51（6）：9-13.

[5]付華.基于極限學習機的半監督分類[D].西安電子科技大學，2013.endprint