基于kd-樹的快速鄰域分類方法

張艷芹, 楊習(xí)貝, 陳向堅

(1.徐州工程學(xué)院 經(jīng)濟學(xué)院, 徐州 221018) (2.江蘇科技大學(xué) 計算機學(xué)院, 鎮(zhèn)江 212003)

粗糙集理論[1]經(jīng)歷了近40年的發(fā)展,因其不同種類的變型[2]易于適應(yīng)各種結(jié)構(gòu)復(fù)雜、種類繁多的數(shù)據(jù)分析需求,在眾多領(lǐng)域得到了成功的應(yīng)用．在各類粗糙集的擴展模型中,文獻[3-5]中提出的鄰域粗糙集方法尤其引人關(guān)注．這主要是因為鄰域粗糙集方法采用距離度量來構(gòu)建鄰域信息粒,不僅可以有效處理連續(xù)型數(shù)據(jù),還可以對符號型與連續(xù)型共存的混合數(shù)據(jù)進行分析[6-12]．除此之外,更為重要的是鄰域粗糙集利用半徑來控制樣本間的距離,以判定不同樣本是否屬于同一鄰域信息粒,因此在不同半徑下,自然地為鄰域信息粒構(gòu)建了一個多粒度結(jié)構(gòu)．這種多粒度結(jié)構(gòu)符合人類分層遞階的認知機理與自然思維模式．

以鄰域粗糙集模型為基本框架，文獻[3-4]中提出了一種基于多數(shù)投票原則的鄰域分類方法(NC),其過程主要分為基于鄰域粗糙集的特征選擇和基于多數(shù)投票原則的鄰域分類兩大部分．NC無論是在特征選擇階段,還是在鄰域分類階段,最為關(guān)鍵的步驟是鄰域信息粒化.例如利用較小半徑所得到的鄰域信息粒化在一些分類問題上往往能夠展現(xiàn)較好的性能,但這并非絕對事實,當(dāng)樣本分布不平衡時,小半徑反而會對小類樣本的判定帶來困擾．鑒于此,近年來有關(guān)鄰域信息粒化方法的研究大多以提升鄰域分類的準確率為目的,試圖探尋一種數(shù)據(jù)自身性質(zhì)驅(qū)動的鄰域半徑自適應(yīng)方法；很少有人注意到良好的鄰域搜索方式對提升NC效率的重要現(xiàn)實意義．眾所周知,已有的鄰域信息粒化方法通過線性掃描來尋找特定樣本的鄰域空間．當(dāng)數(shù)據(jù)規(guī)模較為龐大時,線性掃描基于的鄰域搜索方式將會因需要遍歷所有樣本而變得非常耗時．

kd-樹作為一種對k維空間中的樣本進行存儲，以便對其進行快速搜索的樹形數(shù)據(jù)結(jié)構(gòu),已被廣泛應(yīng)用于聚類分析[13]、圖像匹配[14]、信息檢索等領(lǐng)域．kd-樹是對k維空間進行劃分的二叉樹,其每個結(jié)點對應(yīng)于一個k維超矩形區(qū)域,利用kd-樹可以省去對大部分樣本的搜索,從而減少搜索的計算量．為此,文中將借助kd-樹這一可被用于快速樣本搜索的樹形結(jié)構(gòu),提出一種基于kd-樹的快速鄰域分類方法kdtree-NC,該方法在特征選擇與鄰域分類兩階段的信息粒化過程中,均采用基于kd-樹的快速鄰域搜索方式，代替?zhèn)鹘y(tǒng)NC中的線性遍歷搜索．

1 相關(guān)工作

1.1 鄰域粗糙集

分類學(xué)習(xí)任務(wù)可表示為四元組,其中,U={x1,x2,…,xn}，表示所有n個研究樣本構(gòu)成的集合,稱為論域;A={a1,a2,…,am}，為描述論域中所有樣本的特征集合;Va為特征a的值域;f:U×A→V為信息函數(shù)．特別地,若A=C∪D,C為條件特征集合,D為決策特征,那么分類學(xué)習(xí)任務(wù)可被視作一決策系統(tǒng)DS．

定義1[3]給定任意一樣本xi∈U,B?C,特征集合B下xi的鄰域δB(xi)可定義為:

δB(xi)={xj|xj∈U,ΔB(xi,xj)≤δ}

(1)

式中：δ為鄰域半徑；Δ為度量函數(shù)；?xi,xj,xk∈U,特征集合B下樣本間的度量函數(shù)ΔB滿足:

(1) 非負性:ΔB(xi,xj)≥0, 其中ΔB(xi,xj)=0當(dāng)且僅當(dāng)xi=xj;

(2) 對稱性:ΔB(xi,xj)=ΔB(xj,xi);

(3) 三角不等式:ΔB(xi,xj)≤ΔB(xi,xk)+ΔB(xk,xj).

目前,已有大量的度量函數(shù)被廣泛使用[15]．給定m維特征空間A={a1,a2,…,am}中的兩個樣本xi和xj,f(x,ai)表示樣本x在第ai維上的特征值,那么曼哈頓距離、歐式距離以及高斯距離分別定義:

(2)

(3)

(4)

在定義1中,δB(xi)是由樣本xi在特征集合B下誘導(dǎo)的鄰域信息粒,其大小依賴于鄰域半徑δ的選取,δ越大,將有越多的樣本落入到xi的鄰域空間中．若特征集合B誘導(dǎo)了一系列的鄰域信息粒,則決策系統(tǒng)可被稱為鄰域決策系統(tǒng)NDS．

定義2[3]給定一鄰域決策系統(tǒng)NDS=,δB(xi)是由樣本xi在特征集合B?C下誘導(dǎo)的鄰域信息粒,?S?U,特征集合B下S的下、上近似集合分別定義:

(5)

(6)

定義3給定一鄰域決策系統(tǒng)NDS=,U/IND(D)={πd1, πd2,…, πdp}是由決策特征D誘導(dǎo)的論域上的劃分,?B?C,決策特征D相對于條件特征集合B的鄰域依賴度可用γ(B,D)表示,其定義:

(7)

式中：|·|為集合的基數(shù)；?πdi∈U/IND(D)；πdi為一決策類．

鄰域依賴度γ(B,D)度量了特征集合B誘導(dǎo)的粒化空間對決策D上各決策類的近似能力．在鄰域決策系統(tǒng)中,鄰域依賴度具有單調(diào)性,即若B1?B2,則γ(B1,D)≤γ(B2,D)成立,在此基礎(chǔ)上,可以設(shè)計出鄰域粗糙集下的特征選擇方法．

定義4給定一鄰域決策系統(tǒng)NDS=,?B?C,B為C的一個約簡，當(dāng)且僅當(dāng)滿足:

(1)γ(B,D)=γ(C,D);

(2) ?B′?B,γ(B′,D) ≠γ(B,D).

由定義4可知,條件特征C的約簡是保持決策特征D的鄰域依賴度不變的最小子集．在實際應(yīng)用問題中,上述約簡的限制條件過于嚴格,已有學(xué)者在對約簡條件進行適當(dāng)放寬的基礎(chǔ)上,提出了ε-約簡[15],即滿足:

(1)γ(B,D)≥(1-ε)·γ(C,D);

(2) ?B′?B,γ(B′,D) < (1-ε)·γ(C,D).

ε-約簡旨在保持決策特征D的鄰域依賴度變化在一個較小的范圍內(nèi)時,盡可能多地消除冗余或無關(guān)的特征,一般而言,ε在0～0.1之間取值．當(dāng)ε=0時,ε-約簡退化為定義4中的約簡定義．

1.2 鄰域粗糙特征選擇

在分類學(xué)習(xí)任務(wù)中,特征選擇是一種可以有效地消除冗余和無關(guān)特征的技術(shù)手段．鄰域粗糙集框架下的特征選擇旨在找出和原始條件特征集合具有相同刻畫能力的最小特征子集[16]．

定義5給定一鄰域決策系統(tǒng)NDS=,?B?C,?ai∈C-B,ai的特征重要度可定義為:

Sigout(ai,B,D)=γB∪{ai},D-γ(B,D)

(8)

Sigout(ai,B,D)反映了特征ai加入特征集合B前后，決策特征D的鄰域依賴度的變化程度．基于上述特征重要度的定義,貪心搜索策略可通過迭代，選出鄰域決策系統(tǒng)中最重要的特征子集．

算法1:基于鄰域粗糙集的特征選擇算法

輸入:鄰域決策系統(tǒng),鄰域半徑δ1,允許誤差ε．

輸出:特征子集B．

步驟：

(1)B←?;

(2)?ai∈C,計算Sigout(ai,B,D),其中γ(?,D)=0;

(3) 選擇特征aj按照:Sigout(aj,B,D)=

max{Sigout(ai,B,D): ?ai∈C};

(4) 當(dāng)γ(B,D) < (1-ε)·γ(C,D)時:

(4.1)B←B∪{aj};

(4.2) ?ai∈C-B,計算Sigout(ai,B,D);

(4.3) 選擇特征aj按照:Sigout(aj,B,D)=max{Sigout(ai,B,D): ?ai∈C-B};

(5)輸出特征子集B．

算法1通過迭代，將能夠最快速增加鄰域依賴度的特征加入到已選特征集合中,直到所選特征下決策特征D的鄰域依賴度為原始特征集合的100·(1-ε) %時算法停止．

1.3 鄰域分類器

鄰域分類器在未知樣本的鄰域空間內(nèi),采用多數(shù)投票原則,對未知樣本的類別進行判斷．鄰域分類器在思想上與k近鄰算法類似,其不同之處在于鄰域分類器用鄰域半徑替代了近鄰樣本的個數(shù),且可以有效地處理離散型和混合型數(shù)據(jù)．

算法2:鄰域分類器

輸入:訓(xùn)練集(特征選擇后) ,未知樣本y,鄰域半徑δ2．

輸出:預(yù)測的y的類別．

步驟：

(1) ?xi∈U,計算距離ΔB(xi,y);

(2) 找出y的鄰域δ2內(nèi)的樣本集Uδ2(y);

(3) ?πdi∈U/IND(D),P(πdi,Uδ2(y))=|πdi∩Uδ2(y)|/|Uδ2(y)|;

(4) πdj=arg max{P(πdi,Uδ2(y)): ?πdi∈U/IND(D)};

(5) 輸出y的預(yù)測類別j．

2 分類學(xué)習(xí)方法

2.1 kd-樹的構(gòu)造與搜索

kd-樹是把二叉搜索樹推廣到多維數(shù)據(jù)的一種主存數(shù)據(jù)結(jié)構(gòu)．kd-樹是一顆二叉樹,可被視作對k維特征空間的一個劃分．kd-樹的構(gòu)造相當(dāng)于不斷地采用垂直于坐標軸的超平面對k維特征空間切分的過程,從而形成一系列的k維超矩形區(qū)域．

kd-樹一般按照如下方式構(gòu)造:① 構(gòu)造根結(jié)點，根結(jié)點對應(yīng)于包含所有樣本的k維特征空間的超矩形區(qū)域;② 通過遞歸，對k維特征空間切分，在超矩形區(qū)域上選擇某一特定坐標軸和特定切分點,通過垂直于選定坐標軸且經(jīng)過選定切分點的超平面，將當(dāng)前超矩形區(qū)域劃分為左右兩個子區(qū)域(左子樹和右子樹),該超矩形區(qū)域上的所有樣本被劃分入左右子區(qū)域中．當(dāng)左右子區(qū)域中沒有樣本時,遞歸過程終止．

為了使構(gòu)造的kd-樹平衡,通常將各個維特征依次作為選定的坐標軸,切分點采用所有樣本在選定坐標軸上的中位數(shù)．

算法3:平衡kd-樹的構(gòu)造算法

輸入:訓(xùn)練數(shù)據(jù)集U={x1,x2,…,xn},其中xi=[dim1(xi), dim2(xi),…, dimk(xi)]．

輸出:平衡kd-樹．

步驟：

(1) 選擇dim1為坐標軸,以U中所有樣本的dim1坐標的中位數(shù)為切分點,將根結(jié)點對應(yīng)的超矩形區(qū)域切分成左右兩個子區(qū)域,即用根結(jié)點生成深度為1的左右子結(jié)點,其中左子結(jié)點對應(yīng)坐標dim1小于切分點的子區(qū)域,右子結(jié)點對應(yīng)坐標dim1大于切分點的子區(qū)域;

(2) 對于深度為j的結(jié)點,選擇dimj(mod k)+1為切分的坐標軸,以該結(jié)點區(qū)域中所有樣本的dimj(mod k)+1坐標的中位數(shù)為切分點,將該結(jié)點對應(yīng)的超矩形區(qū)域切分成左右兩個子區(qū)域,即用該結(jié)點生成深度為j+1的左右子結(jié)點,其中左子結(jié)點對應(yīng)坐標dimj(mod k)+1小于切分點的子區(qū)域,右子結(jié)點對應(yīng)坐標dimj(mod k)+1大于切分點的子區(qū)域;

(3) 返回步驟(2),直到左右兩個子區(qū)域沒有樣本;

(4) 輸出平衡kd-樹．

采用kd-樹進行鄰域搜索,可以省去對大部分樣本點的查找,從而減少搜索的計算量．算法4給出了kd-樹下鄰域搜索的具體方法．

算法4:kd-樹下的鄰域搜索算法

輸入:已構(gòu)造的kd-樹,目標樣本x,鄰域半徑δ．

輸出:x的鄰域樣本．

步驟：

(1) 從kd-樹的根結(jié)點出發(fā),通過遞歸，向下訪問kd-樹,如果目標樣本x當(dāng)前維度的坐標小于切分點坐標,那么移動到左子結(jié)點,否則移動到右子結(jié)點,最終到達的葉結(jié)點即為包含x的葉節(jié)點,如果該葉結(jié)點上的樣本到x的距離≤δ,則將該樣本加入到x的鄰域樣本中;

(2)通過遞歸，向上退回,在每個結(jié)點進行操作:

(2.1) 如果該結(jié)點上的樣本到x的距離≤δ,則將該樣本加入到x的鄰域樣本中;

(2.2) 目標x的鄰域樣本一定存在于該結(jié)點一個子結(jié)點對應(yīng)的區(qū)域．檢查該子結(jié)點的父結(jié)點的另一個子結(jié)點對應(yīng)區(qū)域的樣本．檢查另一個子結(jié)點對應(yīng)的區(qū)域是否與以目標x為球心,以δ為半徑的超球體相交．如果相交,可能在另一個子結(jié)點對應(yīng)的區(qū)域中存在與x的距離≤δ的點,移動到另一個子結(jié)點,通過遞歸進行鄰域搜索;否則,向上退回．

(3) 當(dāng)退回到根結(jié)點時,搜索結(jié)束;

(4) 輸出x的鄰域樣本．

2.2 kd-樹下快速鄰域分類方法

文中提出的基于kd-樹的快速鄰域分類方法kdtree-NC仍采用特征選擇和鄰域分類兩個階段,與傳統(tǒng)的鄰域分類方法NC不同的是,kdtree-NC在鄰域信息粒化的過程中,借助可用以實施快速鄰域搜索的kd-樹這一樹形數(shù)據(jù)結(jié)構(gòu),代替了NC方法中基于線性掃描的鄰域搜索方式,在很大程度上減少了需要查找的樣本點,從而降低了鄰域信息粒化中的搜索計算量．

在算法1中,步驟(2)和步驟(4.2)都通過循環(huán)體迭代，尋找能夠最快速增加鄰域依賴度的特征,而鄰域依賴度刻畫了當(dāng)前特征集合所誘導(dǎo)的粒化空間對各決策類的近似逼近能力,因此,算法1的時間開銷主要集中在大量的鄰域信息粒化上．在NC方法中,線性遍歷的鄰域搜索方式的時間復(fù)雜度為O(n),而采用kd-樹方式進行鄰域搜索的平均時間復(fù)雜度為O(logn),一般而言,當(dāng)樣本數(shù)量遠大于特征空間的維度時,kd-樹方式進行的鄰域搜索較線性遍歷方式更為高效．同樣,在鄰域分類器算法(算法2)的步驟1中,也將先采用算法3來構(gòu)造一棵左右平衡的kd-樹,再借助基于kd-樹的鄰域搜索算法(算法4)以提高鄰域決策的時間效率．

3 性能分析

為了驗證基于kd-樹的鄰域分類方法的有效性,文中選取了18組UCI數(shù)據(jù)集進行實驗分析,數(shù)據(jù)集的基本信息如表1．文中實驗選用配備2.7GHz處理器、4GB內(nèi)存的PC機,編程環(huán)境為Matlab 2016b．實驗分為兩個部分：① 對NC和kdtree-NC特征選擇階段的時間消耗進行對比;② 分別比較了特征選擇前后分類的準確率和特征選擇后NC和kdtree-NC方法的分類的時間消耗．

表1 數(shù)據(jù)集基本信息

圖1、2分別展示了鄰域半徑為0.05和0.10時,NC與kdtree-NC中特征選擇的時間消耗,其中黑柱代表NC的時間,白柱代表kdtree-NC的時間．由圖1、2不難發(fā)現(xiàn),在絕大多數(shù)數(shù)據(jù)集上,kdtree-NC中特征選擇的時間消耗要明顯小于NC,僅在Connectionist Bench和Glass Identification數(shù)據(jù)集上,kdtree-NC特征選擇所耗費的時間要略高于NC,其原因在于這兩個數(shù)據(jù)集中的樣本數(shù)與特征數(shù)不滿足kd-樹快速搜索策略中樣本數(shù)應(yīng)遠大于特征數(shù)這一先決條件．

圖1 NC與kdtree_NC特征選擇的時間對比(特征選擇鄰域半徑為0.05)Fig.1 Comparision of elapsed time between NC andkdtree_NC based teature selection(neighbor radius is 0.05)

由表1和圖1、2可知，隨著數(shù)據(jù)集中樣本數(shù)與特征數(shù)之比的增大,NC與kdtree-NC中特征選擇的時間消耗差距也愈發(fā)顯著．

圖2 NC與kdtree_NC特征選擇的時間對比(特征選擇鄰域半徑為0.10)Fig.2 Comparision of elapsed time between NC andkdtree_NC based teature selection(neighbor radius is 0.10)

圖3、4分別為特征選擇鄰域半徑為0.05和0.10時,對NC與kdtree-NC的分類性能進行對比．在鄰域分類階段,在30個鄰域半徑(0.01～0.30,間隔為0.01)下,文中比較了NC與kdtree-NC的分類時間消耗．在每個鄰域半徑點,實驗采用了10折交叉驗證的方式，分類過程重復(fù)10次并記錄整個10次分類的總時間．交叉驗證中共有10組測試樣本集,為此,kdtree-NC方法在分類過程中共需根據(jù)對應(yīng)的10組訓(xùn)練樣本集來構(gòu)建10棵kd-樹用于鄰域搜索．由圖3、4不難發(fā)現(xiàn),在絕大多數(shù)數(shù)據(jù)集的各個鄰域半徑點上,kdtree-NC的分類時間要遠遠小于NC的分類時間,這驗證了文中提出的kdtree-NC，通過采用kd-樹型快速鄰域搜索策略,確實能夠較大程度地縮小鄰域搜索范圍,從而有效地提升鄰域分類的時間效率．

對kdtree-NC在鄰域特征選擇前后的分類精度進行了對比，由圖3、4可見，在大部分數(shù)據(jù)集上,特征選擇后的鄰域分類精度要高于特征選擇前,這說明算法1可以有效刪除原始特征空間中的冗余信息,進而提高鄰域分類準確度．

圖3 NC與kdtree_NC分類性能的對比(特征選擇鄰域半徑為0.05)Fig.3 Comparision of classification performances between NC and kdtree_NC(neigbbor radius is 0.05)

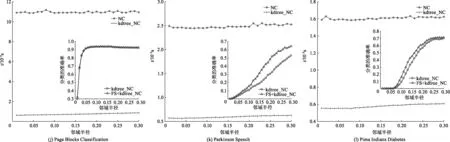
圖4 NC與kdtree_NC分類性能的對比(特征選擇鄰域半徑為0.10)Fig.4 Comparision of classification performances between NC and kdtree_NC(neigbbor radius is 0.10)

4 結(jié)論

(1) 文中通過kd-樹型鄰域搜索策略,提出了一種基于kd-樹的快速鄰域分類方法kdtree-NC,該方法在鄰域信息粒化過程中采用了kd-樹搜索策略代替了傳統(tǒng)鄰域分類方法中的線性遍歷搜索,有效地降低了鄰域搜索的時間開銷．

(2) 在18組UCI數(shù)據(jù)集上的實驗結(jié)果表明,與傳統(tǒng)的鄰域分類方法相比,kdtree-NC在特征選擇和鄰域分類階段的時間效率都有顯著提升．

(3) 在下一步的研究工作中,筆者計劃將ball-樹搜索結(jié)構(gòu)引入到鄰域分類方法中,以解決kdtree-NC在處理高維特征數(shù)據(jù)時效率急劇降低的不足．