基于Hurst指數的軟件失效數據長相關特征分析

王哲璇 尹俊添 魯銳

摘要 Hurst指數反映了事物發展過程的長記憶性程度，揭示了事物發展過去、現在和未來之間的內在聯系，并以時間序列的自相似性和長程相關性體現了事物的發展變化情況。本文基于Hurst指數，對軟件失效時間間隔數據進行Ma tlab處理，進而分析得到其長程相關性。并通過移動Hurst指數處理，獲得更為準確的分析結果。

【關鍵詞】Hurst指數 移動Hurst 指數 長相關特征 軟件失效

1 引言

在當今社會，計算機技術飛速發展。人類對于計算機系統需求的增長，要求人類設計、實現、測試和維護這些系統的能力應得到相應的提升，否則將產生嚴重的計算機失效危機。顯然，提高計算機軟件系統的可靠性，對于計算機開發者以及軟件維護人員來講，是一個艱巨且重要的挑戰。

2 分析方法

2.1 Hurst指數

Hurst指數是水利專家Hurst在研究尼羅河水庫水流量和貯存關系時，提出的用來描述分形布朗運動特性的參量。Hurst指數反映了事物發展過程的長記憶性程度，揭示了事物發展過去、現在和未來之間的內在聯系。通過研究Hurst指數隨時間尺度的變化規律，可合理預測事物變化發展的趨勢。在估計Hurst指數時，R/S分析法（重標極差法）最為常用。

log（R/S）n=Hlogn+loga

式中，R/S為重標極差，a和H為常數，稱H為Hursr指數。用最小二乘法對log（R/S）。與logn作回歸，回歸直線的斜率即為Hurst指數H的估計值。

2.2 Hurst指數與長程相關性的關系

（1） H=l/2時，該時間序列為獨立同分布的隨機序列，即過去狀況與未來趨勢之間不存在相關性。

（2）H≠1/2時，該時間序列為非隨機序列，即過去狀況與未來趨勢之間有關。

（3） 1/2

（4） O

3 分析對象

本文利用間隔時間單位為秒的軟件失效時間間隔數據進行Hurst指數分析。數據來源于軟件失效測量系統SYS3的檢測結果，共有數據207個。

前三個數據為：39，10，4。以前三個數據為例，我們對數據含義進行解釋：第一次軟件失效與第二次軟件失效的時間間隔為39秒，第二次軟件失效與第三次軟件失效的時間間隔為10秒，第三次軟件失效與第四次軟件失效的時間間隔為4秒。我們利用以上數據來進行Hurst指數估計。

4 計算軟件失效的Hurst指數

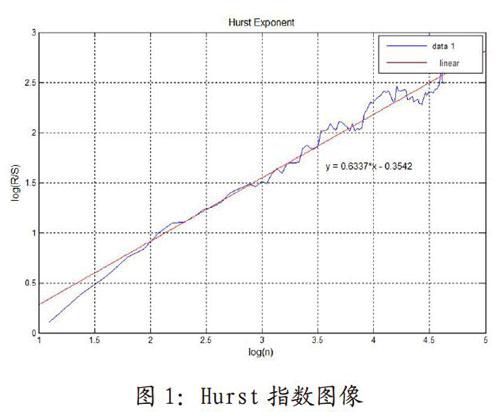
如圖1所示，通過運行我們編寫的MATLAB程序，我們獲得了Hurst指數的圖像，趨勢為一條向右上方傾斜的曲線，波動范圍較小，類似于線性圖像。因此我們利用線性擬合，做出該圖形的線性擬合圖像。由R/S分析法知，該線性圖形的斜率即為Hurst指數。結果為H=0.6337>0.5。通過在本文第二部分的分析中我們可以了解到：這組數據序列具有長期相關性（或稱長期記憶性），即未來趨勢與過去趨勢一致，且對初始條件有敏感依賴性。盡管序列相關性并不強，但在一定程度上說明軟件失效時間并沒有呈現出隨機游走的特性，并不是一個獨立過程，而是表現出相互依存的關系。這表明進行軟件時間間隔的分析是有規律可循的。從另一方面來講，說明了在未來的研究中，我們可以進一步探究失效時間的規律性，可以進行下次失效時間的預測。

5 計算軟件失效的移動Hurst指數

5.1 移動Hurst指數

Hurst指數能進行長程相關性的分析，但是無法分析信號的時變特性，因此我們接下來將引入移動Hurst指數。移動Hurst指數即對單步的Hurst指數進行移動平均處理，使處理后的Hursr指數序列，既保留了原Hurst指數序列的趨勢性，又提出Hurst指數波動的偶然性波動。由于移動Hurst指數反復計算了序列，所以比原始的Hurst指數有更好的準確性和代表性。我們可以更加確信通過移動Hurst指數獲得的結果。同時也從側面證明了Hurst指數確實可以表明序列是均值回復還是反持久性的。

5.2 計算軟件失效的移動Hurst指數

通過數據波形與移動Hursr指數圖2我們可以發現：

（1）移動Hurst指數大部分時間位于0 5以上，與Hurst指數計算結果相符。表示軟件失效時間并沒有呈現出隨機游走的特性，不是一個獨立過程，而是表現出相互依存的關系。因此對于軟件失效時間間隔分析是有規律可循的。

（2）由圖2我們看到，數據波形與Hurst移動平均指數均是曲線形狀，且走勢類似。但有部分點存在原始數據波形與Hurst移動指數呈現出相反趨勢的情況。將圖形放大，得到接下來放大了的前一百個數據局部圖3。

通過前一百個數據的放大的局部數據波形與移動Hurst指數圖3，我們可以發現：

圖像中可以找到一些異常點，如50，57，99。在原始數據波形中，第50號、57號數據在局部中一直處于上升趨勢;而在移動Hurst指數圖像中，兩點所在位置均為局部的最低點。這表明，第50號、第57號數據有極大可能為異常點，將不再符合原來趨勢上升，而是在接下來一段時間內出現下降趨勢。而第99號數據與以上兩點相反，因具有局部最高的移動Hurst指數，原始數據很有可能不再符合原始規律繼續下降，而是轉為上升。在第100號數據以后的107個數據中，具有此類性質的還有第136，第147，第196號數據等等。這說明，在總體情況下，移動Hurst指數表征了數據的長程相關性，但同時也存在一些異常點，也可稱作離群點。在以后的研究中，要注意到此類數據的存在，特殊處理，才能達到最優的分析效果。

6 結語

本文基于Hurst指數，進行了軟件失效數據時間間隔的數據處理與分析。通過Matlab軟件計算Hurst指數，得到其結果大于0.5，表明了本數據的長程相關特性。此外，應用了移動Hurst指數，進行了更為準確的分析處理，發現處理結果與Hurst指數處理結果基本相符，但同時也發現仍存在少量異常點，這些數據需要在今后分析中進行特殊處理。在未來的工作中，計劃建立Hurst指數與系統負載、故障事件之間的關聯，診斷出導致軟件失效衰退的構件，規避軟件失效，實施積極的恢復策略。

參考文獻

[1]呂金虎.混沌時間序列分析及其應用[M].武漢：武漢大學出版社，2015： 157 -160.

[2]葉建萍，資本市場的Hurst指數估計[D].廣西師范大學，2010.

[3]謝幼瓊，顧圣平，城市用水時間序列的Hurst指數研究[J].水電能源科學，2012，30 （12）： 27-29.

[4]徐建，張琨，游靜，劉鳳玉，基于分形的軟件衰退預測[J].系統仿真學報，2007 （03）：549-551.