基于D-S證據理論的智能溫室環境控制決策融合方法
孫力帆 張雅媛 鄭國強 冀保峰 何子述
(1.河南科技大學信息工程學院, 洛陽 471023; 2.電子科技大學電子工程學院, 成都 611731)
0 引言
現代智能溫室環境控制系統受到越來越多的關注,與此相關的無線傳感器網絡信息融合技術更是得到了廣泛應用[1-5]。無線傳感器網絡下智能溫室環境控制的核心是智慧管理和智能決策,即使用大量密集部署在溫室監控區域的智能傳感器節點對溫室大棚內溫濕度、光和有效輻射、二氧化碳、光照等小氣候環境參數數據進行自動采集和分析,以智能調控溫室達到適宜植物生長的范圍。但是,由于受到外部環境和無線傳感器內部構造等多種因素的影響,傳感器測得的數據往往具有一定不確定性,而Dempster-Shafer(D-S)證據理論能夠對其進行有效處理,且具有很強的靈活性和可靠性,已被許多專家系統所應用。盡管證據理論有許多優點,但當證據之間存在高度沖突時,D-S證據理論的處理結果往往與常理相悖。目前,解決證據沖突問題主要有以下2類方法:①在不改變融合規則的前提下,對傳感器量測數據進行預處理,即采用剔除異常數據的方法或聚類分析,以減少數據波動,從而使得數據在決策融合之前達到理想狀態降低證據沖突程度,提高融合精度[6-12]。雖然能從不同程度上減少證據沖突帶來的數據誤差,降低數據間波動對融合結果的影響,但是它們幾乎都是剔除掉原始數據中存在的異常值,必然導致樣本數據減少,不利于提高后續的整體融合精度。②通過改進證據理論融合規則以達到融合后置信函數的合理分配,或在融合之前選取各個證據最優的信度函數[13-22]。當證據間高度沖突或者完全沖突時,雖然修改證據理論融合規則可以使置信函數合理分配,但是這種做法有可能破壞證據融合中的交換律、結合律等優良特性,不能真正達到降低沖突程度的目的。
上述兩類方法在處理決策融合時均具有一定局限性。本文結合它們各自優點提出一種溫室環境控制決策融合框架。首先,使用箱線圖檢測出原始量測數據中存在的異常值;然后對其進行預處理,提出一種異常數據自適應修正算法以減少誤差,并對修正更新完成后的數據進行系統聚類;最后,根據本文提出基于加權相似度的基本概率分配(Basic probability assignment, BPA)方法結合D-S證據理論進行數據融合。
1 數據預處理
1.1 異常數據自適應修正算法
一般地,傳感器測量數據往往都是隨機的且有可能存在異常值,是指測量數據集合中嚴重偏離大部分數據所呈現趨勢的小部分數據點,由于傳感器自身或數據傳輸的原因,使得測量數據序列中存在某些錯誤的測量。數據中存在的異常值會使后續的決策融合結果嚴重偏離預想狀態,繼而產生較大誤差。常用檢測異常值的方法有3δ法則、狄克遜準則和z分數方法等。以上方法均是假定測量數據呈正態分布,而實際上它們的分布往往是未知的,此外,這些方法判斷異常值的標準是通過計算批量數據的均值和標準差來實現,但是以上2個統計量易受異常值約束,使得異常數據檢測率偏低。本文采用箱線圖檢測并對其自適應修正。
定義1:箱線圖是用來體現數據分散情況的統計圖,可以表示數據的分布差異,它由5個數據統計量組成:最小值Xmin、下四分位數Q1、中位數Q2、上四分位數Q3、最大值Xmax。箱線圖結構如圖1所示,紅色圓圈為異常值標記。

圖1 箱線圖結構Fig.1 Structure of box-plot
待統計數據按從小到大排列X:(x1,x2,…,xN),中位數Q2定義為第50%數據,下四分位數Q1定義為第25%數據也可定義為[Xmin,Q2]的中位數,上四分位數Q3定義為第75%數據同理可定義為[Q2,Xmax]的分位數[9]。以6個數據為例,按其從小到大順序排列為x1,x2,…,x6,具體計算方法為:
Q1的位置
(1)
Q2的位置
(2)
Q3的位置
(3)
異常點的上下邊緣為
(4)
其中
IQR=Q3-Q2
式中IQ——Q1與Q3之間的距離FU——異常值上邊緣分界點FI——異常值下邊緣分界點
顯然,使用箱線圖對數據分布進行描述,異常值清晰可見。其判斷標準是大于Q3+1.5IQR或者小于Q1-1.5IQR(即式(4)中β=3),經驗表明該標準的選取在處理批量數據時有較高的魯棒性。相較于現有主流的3δ法則、狄克遜準則等異常值檢測方法,箱線圖的優勢在于它從實際數據出發,無需假設其統計分布,并且四分位數表示形式不易受異常數據影響。
針對異常數據的處理通常采用直接將其剔除的辦法,但是僅僅剔除異常值不但會使樣本數量減少,而且有可能使得每組數據的維數不盡相同,從而導致精度降低。因此,本文提出了一種基于專家系統的異常數據自適應修正算法,能夠在不改變樣本數量的前提下通過對其進行修正,提高批量數據的魯棒性。
在文獻[9]的溫室控制專家系統表中,4種決策分別對應的環境參數為25.3、31.3、39.3、35.4℃,則所提出的算法根據以上均值進行如下修正。
情況1:x1>xm,Δ=x1-xm
(5)
(6)
(7)
情況2:x1 (8) (9) (10) 式中x1——異常值xm——專家系統值——修正值 一般地,溫室大棚中的小氣候參數,如溫度、光照強度和二氧化碳體積分數的原始量測數據(含異常值)范圍是在專家系統均值上下波動不超過15 (不包括量綱),只是溫度和光照強度波動范圍會比二氧化碳體積分數小一些。文中分3段依次對其進行修正,其最終目的是讓異常值逐漸收斂于專家系統值。 情況1:異常值x1大于專家系統均值xm時,其差值記為Δ,為修正后值,當Δ≤5時,則=x1-Δ/2,稱為1次收斂運算;當5<Δ≤10,對異常值進行2次收斂運算;當5<Δ≤10,則對異常值進行3次收斂運算。 情況2:異常值x1小于專家系統均值xm時,其差值記為Δ,為修正后的值,當Δ≤5時,=x1+Δ/2,同樣稱為一次收斂運算;當5<Δ≤10與5<Δ≤10時,與情況1一樣分別對異常值進行2次、3次收斂運算。當所有異常值修正完成后,通過箱線圖觀察更新數據是否還有異常值,如果有,繼續對其進行修正直至沒有異常值。本文研究表明,完成全部數據更新一般不超過3次迭代修正。 當所有數據更新完成后,需要對個數較多且分散的數據聚類融合分析使之系統化。本文首先利用凝聚的層次聚類對數據處理,把每個數據作為一類,計算數據距離并根據類間距離進行合并直至所有數據都歸為一類。 (11) 由式(11)可得馬氏距離矩陣 (12) 根據式(12)中Dn(X)選取不同的距離準則對修正后的數據進行聚類:一是使用最小距離聚類準則首先在Dn(X)中查找最小值,然后將距離最小的這2個數據進行聚類得到新的一類值,再重新計算距離矩陣,依次聚類得到最終的聚類值。二是使用平均加權距離聚類準則對分布密集的數據進行聚類,繼而最終將其歸為一類。研究表明,2種距離準則下的聚類結果基本一致,但使用加權平均距離可得到比最小距離更高的聚類精度,且更接近實際。 2 基于D-S證據理論的溫室環境控制決策融合 溫室環境控制系統的目的是根據農作物實際生長需求做出某種控制決策,但直接使用上述聚類融合處理后的數據仍然會因其本身所具有的不確定性而產生一定誤差,以致無法精確調控溫室達到適宜農作物生長的范圍。本文引入D-S證據理論來解決數據不確定性所產生的誤差而帶來的決策風險問題。 D-S證據理論是將2個或多個基本概率分配函數通過理論規則融合成新的概率分配函數,并將其作為最終的決策依據,用以提高整個決策可靠性。 (1)基本概率分配函數(BPA) 在溫室環境控制系統中,假設所有可能的決策結果組成一個完備集合Θ,其中各個元素相互獨立。那么,Θ中各焦元的m函數分配定義為 m:2Θ→[0,1] 滿足 (13) 其中滿足m(Ai)>0的元素Ai稱為焦元,Ai(i=1,2,…,n)∈Θ。 (2)m函數合成規則 ?Ai,Ai(i=1,2,…,n)∈Θ均不為空集,Θ上n個m函數m1,m2,…,mn的合成規則為 (14) 當證據之間存在高度沖突時,直接使用上述經典證據理論有可能會偏離實際結果而做出錯誤判斷。本文提出了一種基于加權相似度的概率分配算法。 在1.2節中得到的聚類值集合X表示為(x1,x2,…,xn),專家系統均值集合ω表示為(ω1,ω2,…,ωn),辨別框架Θ表示為(L1,L2,L3,L4),其中Li(i=1,2,3,4)代表最終的4個決策內容。以數據x1為例進行分析,首先根據聚類值與系統均值之間的距離得出相似度,相似度越高說明此數據的信任度越高、概率分配也越高,然后根據加權系數進行調整。令ω1≤x1≤ω2,ω1和ω2分別對應的決策為L1和L2,分別計算x1與ω1、ω2的距離和相似度為 (15) (16) 式中d1——x1與ω1的距離d2——x1與ω2的距離s1——x1與ω1的相似度s2——x1與ω2的相似度 由式(15)、(16)可知距離越小,兩者的相似度越大。如果d1>d2,則表明x1相較于ω1更接近ω2,對決策L2也更信任,則所提出的基本概率分配函數為 (17) 參數ρ1和ρ2的設定是為了避免信任度過大而偏離實際結果,實驗表明ρ1=3、ρ2=5時結果最為精確。 實驗采用文獻[9]中提到的溫度(℃)、光照度(klx)、二氧化碳體積分數(μL/L)這3個環境參數,并選取早中晚6個時刻對以上3個參數進行數據采集。每個時刻的每個參數各采集26個數據,記為X:(x1,x2,…,x26),決策結果共分為4個:開啟卷膜、開啟卷膜和啟動風機、啟動風機與濕簾、無動作,即D:(L1,L2,L3,L4)。最后,按照本文提出的方法在每個時刻對各個環境參數下的測量數據進行聚類,并根據同一時刻的3個環境參數做出決策。 以傳感器采集到的溫度數據為例,圖2和圖3分別是6個時刻原始數據和修正后數據的箱線圖表示。由圖3可以看出,箱線圖的箱體寬度不一,中位數的位置也不同,這取決于測量數據的分散程度和傳感器的精確度,但是數據整體呈正態分布,中午溫度最高,早晨和傍晚溫度較低。顯然,圖中每個時刻原始溫度數據都存在異常值,而修正之后數據如圖3所示,可見修正后異常數據不復存在,且沒有改變原始數據的統計分布。 圖2 原始溫度數據分布圖Fig.2 Distribution of raw temperature data 圖3 修正后的溫度數據分布圖Fig.3 Distribution of corrected temperature data 接下來,本文對箱線圖和狄克遜準則的異常數據檢測率進行對比,如圖4所示,由圖4可見,箱線圖的異常數據檢測率相比于狄克遜準則提高了約19.2%,該方法更為有效。 圖4 異常數據檢測率Fig.4 Detection rate of outlier data 在加權平均距離準則和最小距離準則下對修正異常數據后與直接剔除異常數據后的聚類結果進行對比(圖5和圖6)。特別在無線傳感器網絡下的智能溫室環境控制系統中,由于需要檢測和收集大量的傳感器量測數據,需要首先著重考慮異常數據的處理工作是否會影響溫室環境控制系統的穩定性,因為它是評估系統性能的根本標準。相應地,穩定性就作為一個關鍵評價指標被用來判定不同方法的性能。雖然直接剔除法減少了異常數據對環境控制決策所產生的不利影響,但是這種做法會造成后續聚類結果上下波動,不僅有可能導致錯誤的控制決策產生,而且更關鍵是增加了環境控制系統不穩定的風險。由圖5、6可以得到,直接剔除異常值后的聚類值雖然接近專家系統值(因其直接剔除掉異常數據這一不利因素),但是相對于專家系統值波動過大,極其不穩定。而修正后的聚類值則完全根據專家系統值的變化而變化,也就是它們的聚類趨向一致,性能也更為穩定。實際的智能溫室控制系統中分布著大量的傳感器,則使用剔除法勢必會帶來更大的聚類性能波動,從而嚴重影響控制系統的穩定性,因此本文提出的自適應修正的方法更為穩健和優異。 圖5 加權平均距離準則下異常數據剔除、修正后的聚類結果對比Fig.5 Clustering comparison after removing or correcting outliers using weighted average distance 圖6 最小距離準則下異常值剔除、修正后的聚類結果對比Fig.6 Clustering comparison after removing or correcting outliers using minimum distance 此外,還對異常數據修正后2種不同距離準則下的聚類結果進行對比(圖7),由圖7可得,使用平均加權距離更接近專家系統值。這是因為異常值修正后的大部分數據都與專家系統值相差無幾且分布較為密集,在平均加權距離準則下對分布居中的數據進行聚類,能夠使其信任度升高。而在最小距離準則下其聚類結果有可能受到分散數據的影響,因此需要首先對離散點進行聚類,但這樣處理會加大離散點的信任度。顯然,使用平均加權距離準則對異常值修正后的數據進行聚類更符合實際。 圖7 兩種不同距離準則下異常數據修正后的聚類結果對比Fig.7 Clustering comparison after correcting outliers using two different distances 修正異常值后的數據在2種距離準則下的聚類性能對比如圖8所示,由圖8可以看出,加權平均距離下的聚類性能較為穩定且總體高于最小距離下的聚類性能。這里特別注意的是,雖然最小距離相較于加權平距離下的聚類性能相差不大(在0.1以內),但是前者明顯波動較大,其聚類結果不夠可靠,顯然不能被后續融合處理所采用。以上性能對比結果分析再次印證了修正數據聚類使用加權平均距離準則比最小距離準則魯棒性更高,適用性更強。 圖8 兩種不同距離準則下異常數據修正后的聚類性能對比Fig.8 Comparison of clustering performance after correcting outliers using two different distances 為了驗證所提出基于加權相似度概率分配函數對于溫室環境控制決策融合的有效性,本文與文獻[9]提出的決策融合方法進行了對比分析。依次選取了4組數據進行基本概率分配實驗,2種方法的概率分配分別如表1和表2所示,其決策融合對比結果見表3。從表1、2可以看出,2種方法的基本可信度分配效果一致,其中t、c、i分別代表溫度、光照度、二氧化碳體積分數,但是,文獻[9]提出的方法(采用均值劃分)中不確定的基本概率分配全部為默認的0.1(表1)。但由于每個時刻不同溫室環境參數下的數據不同,傳感器精度也不同,不確定的基本概率分配也必然不同,那么顯然該方法并不符合實際。 表1 基本均值劃分的概率分配表Tab.1 Probability allocation of basic mean division 表2 基于加權相似度的概率分配表Tab.2 Probability allocation based on weighted similarity 對比表1、表2中提出的基于加權相似度的概率分配方法,能夠根據實際情況嚴格按照更新數據與專家系統值進行對比加權,從而大大減少了經驗選取所帶來的風險。此外,本文的方法相比文獻[9]中的方法不但在不確定的基本信度分配上降低了1~2個數量級,而且有效地減小了數據間的沖突程度,使得同一樣本間各環境參數信任度高度匹配。 本文對兩種方法中證據理論融合后的概率分配進行比較(表3),可以看出,相比于文獻[9],本文的方法提高了判斷精度使得決策結果更加準確。特別注意的是,文獻[9]中基于平均劃分的融合結果表明其不確定性融合精度為10-3,而從本文提出的基于加權相似度融合結果中可以觀察到不確定性融合精度降為10-4或10-5,可見融合后的不確定性大幅度降低(即1~2個數量級),表現了極快的收斂速度。 表3 兩種方法的融合結果對比Tab.3 Comparison of fusion results in two approaches (1)通過采用箱線圖法檢測原始數據的異常值,可以達到比現有方法更高的檢測率,最高可以達到22.3%。 (2)在不改變樣本數量的前提下,提出了一種異常數據自適應修正算法,有效降低了異常數據對聚類性能的影響,且修正后的數據聚類使用加權平均距離準則比最小距離準則穩定性更強。 (3)為了使基本概率分配更加合理,提出了一種基于加權相似度的函數方法,并將此方法應用在溫室環境控制決策融合中。實驗對比結果表明,本文提出的方法簡單有效,不但能夠將證據的不確定程度降低1~2個數量級,而且有效地降低了數據之間的沖突程度,有利于快速做出正確決策。 1 李昌璽, 周焰, 林菡, 等. 考慮傳感器置信度的改進D-S證據合成算法[J]. 解放軍理工大學:自然科學版, 2017, 18(1): 81-86. LI Changxi, ZHOU Yan, LIN Han, et al. Improved D-S evidence combination rule based on reliability of sensors[J]. Journal of PLA University of Science and Technology: Natural Science Edition, 2017, 18(1): 81-86.(in Chinese) 2 鄧雪峰, 孫瑞志, 聶娟, 等. 基于時間自動機的溫室環境監控物聯網系統建模[J/OL]. 農業機械學報, 2016, 47(7): 301-308.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20160741&flag=1.DOI:10.6041/j.issn.1000-1298.2016.07.041. DENG Xuefeng, SUN Ruizhi, NIE Juan, et al. Greenhouse environment monitoring IOT system modeling based on timed automata[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(7): 301-308.(in Chinese) 3 郭文川, 程寒杰, 李瑞明, 等. 基于無線傳感器網絡的溫室環境信息監測系統[J]. 農業機械學報, 2010, 41(7): 181-185. GUO Wenchuan, CHENG Hanjie, LI Ruiming, et al. Greenhouse monitoring system based on wireless sensor networks[J]. Transactions of the Chinese Society for Agricultural Machinery, 2010, 41(7): 181-185.(in Chinese) 4 何東健, 鄒志勇, 周曼. 果園環境參數遠程檢測WSN網關節點設計[J]. 農業機械學報, 2010, 41(6): 182-186. HE Dongjian, ZOU Zhiyong, ZHOU Man. Design of WSN gateway notes for remote detection of orchards environment parameters[J]. Transactions of the Chinese Society for Agricultural Machinery, 2010, 41(6): 182-186.(in Chinese) 5 李莉, 李海霞, 劉卉. 基于無線傳感器網絡的溫室環境監測系統[J]. 農業機械學報, 2009, 40(增刊): 228-231. LI Li, LI Haixia, LIU Hui. Greenhouse environment monitoring system based on wireless sensor network[J]. Transactions of the Chinese Society for Agricultural Machinery, 2009, 40(Supp.): 228-231. (in Chinese) 6 蔡振江, 康健一, 張青, 等. 數據融合技術在溫室溫度檢測中的應用[J]. 農業機械學報, 2006, 37(10): 101-103. CAI Zhenjiang, KANG Jianyi, ZHANG Qing, et al. Application of multi-sensor data fusion in greenhouse temperature test system[J]. Transactions of the Chinese Society for Agricultural Machinery, 2006, 37(10): 101-103. (in Chinese) 7 溫靜, 程茂. 多傳感器數據融合技術在溫室控制中的應用[J]. 河北農業大學學報, 2015, 38(4): 111-115. WEN Jing, CHENG Mao. Application of multi-sensor data fusion technique in greenhouse control[J]. Journal of Agricultural University of Hebei, 2015, 38(4): 111-115.(in Chinese) 8 駱盈盈, 陳川, 毛云芳. 基于傳感器網絡的K-均值聚類算法研究[J]. 計算機工程與設計, 2007, 28(6): 1349-1351. LUO Yingying, CHEN Chuan, MAO Yunfang. Research on K-means clustering arithmetic based on sensor networks[J]. Computer Engineering and Design, 2007, 28(6): 1349-1351.(in Chinese) 9 王俊, 劉剛. 融合粗糙集和證據理論的溫室環境控制推理決策方法[J]. 農業工程學報, 2012, 28(17): 172-178. WANG Jun, LIU Gang. Decision-making method based on rough set and evidential theory for greenhouse environmental control[J]. Transactions of the CSAE, 2012, 28(17): 172-178.(in Chinese) 10 熊迎軍, 沈明霞, 陸明洲, 等. 溫室無線傳感器網絡系統實時數據融合算法[J]. 農業工程學報, 2012, 28(23): 160-166. XIONG Yingjun, SHEN Mingxia, LU Mingzhou, et al. Algotithm of real time data fusion for greenhouse WSN system[J]. Transactions of the CSAE, 2012, 28(23): 160-166.(in Chinese) 11 宋慶恒, 劉英德, 馬源, 等. 基于多傳感器數據融合的溫室溫濕度控制系統設計[J]. 江蘇農業科學, 2015,43(6):394-396. 12 李富娟, 李仕華, 趙新遠, 等. 溫室控制系統多傳感器數據融合方法的設計[J]. 湖北農業科學, 2016(16): 4287-4289. LI Fujuan, LI Shihua,ZHAO Xinyuan, et al. Design of multi-sensor data fusion algorithm of greenhouse control system[J]. Hubei Agricultural Sciences, 2016(16): 4287-4289.(in Chinese) 13 YANG Y, HAN D, DEZERT J, et al. Comparative study of focal distance measures in theory of belief functions[C]∥2016 19th International Conference on Information Fusion, IEEE, 2016:1308-1315. 14 SHANNON C E. A mathematical theory of communication. AT&T tech J[J]. ACM Sigmobile Mobile Computing & Communications Review, 2001, 5(1): 3-55. 15 DENG Y. Entropy: a generalized shannon entropy to measure uncertainty[J]. 2015. Available online: http:∥vixra.org/abs/1502.0222. 16 WANG J, XIAO F, DENG X, et al. Weighted evidence combination based on distance of evidence and entropy function[J]. International Journal of Distributed Sensor Networks, 2016, 12(7): 3218784-3218784. 17 WANG J, QIAO K, ZHANG Z, et al. A new conflict management method in Dempster-Shafer theory[J]. International Journal of Distributed Sensor Networks, 2017: 1769650. 18 曹建福, 曹雯. 基于改進證據理論的大型制造裝備故障診斷[J]. 振動、測試與診斷, 2012, 32(4): 532-537. 19 劉海波, 殷越, 艾永樂. 基于D-S證據理論的瓦斯突出危險等級評判策略[J]. 濟南大學學報: 自然科學版, 2017, 31(1): 73-76. LIU Haibo, YIN Yue, AI Yongle. Evaluation strategy of gas outburst risk level based on D-S evidence theory[J]. Journal of University of Ji’nan: Science and Technology, 2017, 31(1): 73-76.(in Chinese) 20 李文立, 郭凱紅. D-S證據理論合成規則及沖突問題[J]. 系統工程理論與實踐, 2010, 30(8): 1422-1432. LI Wenli, GUO Kaihong. Combination rules of D-S evidence theory and conflict problem [J]. Systems Engineering-Theory & Practice, 2010, 30(8): 1422-1432.(in Chinese) 21 蔣黎明, 何加浪, 張宏. D-S證據理論中一種新的沖突證據融合方法[J]. 計算機科學, 2011, 38(4): 236-238. JIANG Liming, HE Jialang, ZHANG Hong. New fusion approach for conflicting evidence in D-S theory of evidence[J]. Computer Science, 2011, 38(4): 236-238.(in Chinese) 22 安春蓮, 黃靜, 吳耀云. 基于證據理論的多源信息融合模型[J]. 電子信息對抗技術, 2017, 32(1): 23-26. AN Chunlian, HUANG Jing, WU Yaoyun. A multi-source information fusion model based on evidence theory[J]. Electronic Information Warfare Technology, 2017, 32(1): 23-26.(in Chinese) 23 LIU Z, PAN Q, DEZERT J. Classifier fusion based on cautious discounting of beliefs[C]∥International Conference on Information Fusion, IEEE, 2016.1.2 不同聚類準則下的數據聚類融合


2.1 經典證據理論

2.2 概率分配算法

3 實驗結果與性能對比
3.1 傳感器異常數據檢測及其修正
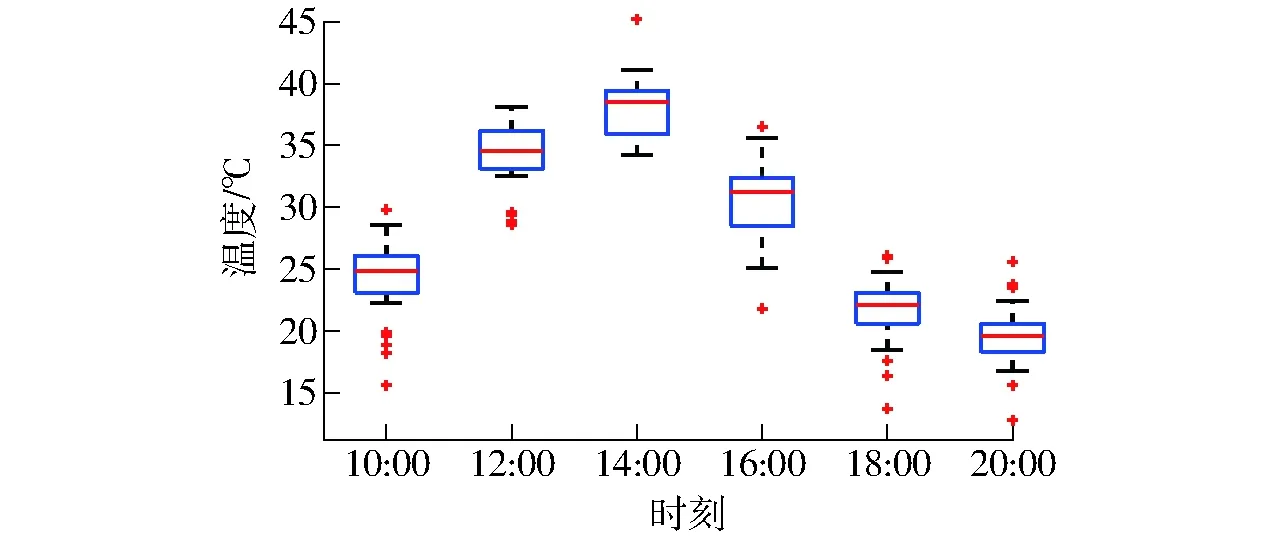


3.2 異常數據剔除、修正后的聚類結果對比


3.3 異常數據修正后不同距離準則下的聚類性能評估


3.4 決策融合結果對比及其性能評估



4 結論

