直線驅動型并聯機器人工作空間分析與優化

吳超宇 錢小吾 余 偉 于 今

(1.重慶大學機械傳動國家重點實驗室, 重慶 400044； 2.鎮江高等專科學校基礎部， 鎮江 212002)

0 引言

根據并聯機器人的結構和關節驅動方式，可以將其分為直線驅動型和旋轉驅動型2種[1]。EPFL的最新研究[2]對直線型并聯機器人和旋轉型并聯機器人的運動特點與機構性能進行了對比分析，旋轉型具有更優良的動態特性，而直線型則具有更大的工作空間，較適應于并聯機床等應用。研究直線驅動并聯機器人工作空間的方法主要有解析法、幾何法和數值法，在解析法方面，JO[3]提出，后經GOSSELIN[4]發展的圓弧相交幾何法,將工作空間邊界構造歸結為12張球面片求交問題。MERLET[5]研究了固定平臺參考點求解相應極限姿態空間的解析方法，解析法精確，但是計算量大，較復雜，不具有通用性。幾何法作圖簡單，但是非常復雜，難以表達機器人的運動，針對直線驅動并聯機器人無法有效得到參數對工作空間的影響趨勢。在數值法研究方面，通常采用數值搜索、牛頓迭代等方法，同時考慮到各關節轉角的約束、各桿長的約束和機構各構件的干涉來確定并聯機器人的工作空間，且采用數值積分的方法計算工作空間的體積，比較接近實際[6-10]。文獻[11-13]提出了一種計算6自由度并聯機器人的定向工作空間的離散化方法。這些方法存在邊界計算不精確，計算量大等問題。在并聯機器人工作空間優化方面，所查閱的文獻中基本上是以工作空間體積最大為優化設計目標，獲取更優良的運動學性能，但是由于旋轉型并聯機器人的整機布局比較緊湊，而直線型并聯機器人的整機布局比較松散，直線型與旋轉型相比，整機結構尺寸比較大，這樣會導致直線型并聯機器人制造成本、占用空間和功率消耗的增加。因此，以工作空間體積最大為優化目標對直線驅動型并聯機器人研究是不合理的。

本文提出一種極坐標變步長迭代搜索法求解出并聯機器人的工作空間，并研究機器人各結構參數對工作空間形狀、大小的影響趨勢，為下一步工作空間優化中設計變量的范圍確定提供了依據。提出一種綜合機構靈巧度與工作空間利用率的全局混合性能指標，針對不同的作業要求，得到兼顧機器人靈巧度與空間利用率的機械結構參數，通過對不同權重下優化得到的參數進行仿真實驗，驗證目標函數的正確性和有效性。通過激光跟蹤儀測出的實際工作空間與理論工作空間模型進行對比，驗證工作空間理論模型的正確性，為后續的尺度綜合研究提供依據。

1 運動學模型

本文研究的直線驅動型并聯機器人如圖1所示，由靜平臺、動平臺、同步帶電缸、滑塊、U型虎克鉸、3組平行四邊形支鏈桿件等組成，每組支鏈分別通過2個虎克鉸(U副)連接動平臺與滑塊，滑塊通過平移副(P副)由同步帶電缸驅動。3組電缸的投影是120°，均勻分布，與水平面呈一個固定的角度，下端交于一點。3個電動機安裝在同步帶電缸的上方，直線驅動3個滑塊，桿件連接處采用一種特殊設計的U型虎克鉸結構，該結構能夠保證平行四邊形兩組桿件的同向性，并能擴大關節的轉動能力。

圖1 直線驅動型并聯機器人三維模型Fig.1 Three dimensional model of linear driven parallel robot1.靜平臺 2.交流伺服電機 3.同步帶電缸 4.滑塊 5.U型虎克鉸 6.平行四邊形支鏈 7.動平臺

圖2是直線驅動型并聯機器人的原理圖，圖3是單個支鏈的原理圖，設定笛卡兒直角坐標O{x,y,z}在靜平臺△A1A2A3的中心O點處并且在動平臺△B1B2B3的中心P處建立一個移動的動笛卡兒坐標P{x′,y′,z′}，由于動平臺與靜平臺平行，并且這個并聯機構只有3個平移自由度，所以x軸與x′軸平行，并且x軸沿著lOA1方向，向量lOA1平行于lPB1，z軸均朝上，3條運動直線DiEi相交于M點，并且與靜平臺相交于Ai(i=1,2,3),并且靜平臺半徑為a。3個長度為l的桿與動平臺相交于Bi,半徑為b,P關節的滑塊在限定的Di與Ei之間移動，α是靜平臺與DiEi導軌的夾角。角度φi是x軸與靜平臺向量lOAi的夾角，因為靜平臺與動平臺平行，所以夾角也適用于動平臺。為了簡化方程，定義

φi=(i-1)×120°

(1)

其中i=1，2，3。在圖3中，Di為同步帶輪的中心點，Ci是經過同步帶輪中心Di沿電缸軸向直線與過滑塊與連桿的虎克鉸中心Fi的垂直電缸導軌直線的交點，Fi是滑塊與連桿的連接虎克鉸的中心，Bi是連桿與動平臺的虎克鉸的中心，P是動平臺的幾何中心，Ei是選定的驅動軸的原點，滑塊到同步帶輪中心Di的距離是di(i=1,2,3)。Hi為滑塊高度，也就是虎克鉸到滑塊的距離。

圖2 直線驅動型并聯機器人原理圖Fig.2 Schematic of linear driven parallel robot

圖3 單支鏈原理圖Fig.3 Schematic of one typical kinematic chain

如圖3所示，點Ai與Bi關于O與P的位置向量可以被寫成

(2)

(3)

左上標向量表示在哪個坐標系中被表達。為了簡潔表述，當在靜平臺的坐標系中被表述時，左上標可以省略。例如Oai=ai，動平臺相對于靜平臺的位置與方向可以由一個方向向量，P=lOP，和一個3×3的旋轉矩陣ORP組成，由于動平臺只有3個平移運動，所以旋轉矩陣ORP也就是一個單位矩陣，所以Pbi=bi，如圖3所示，每一個支鏈的閉環回路方程可以寫成[14]

lei=Li-disi-Hi

(4)

其中

Li=P+bi-ai

(5)

(6)

(7)

式中ei——lFiBi的單位向量di——第i個滑塊的線性位移si——DiEi的單位向量Hi——滑塊高度，它的模長可以表示為|h|是個定值

將式(4)左右兩邊分別點乘本身，可以得

l2=(Li-disi-Hi)(Li-disi-Hi)T

(8)

化簡可以得到

(9)

其中si與Hi是垂直的2個向量，所以si與Hi的乘積是0。式(9)可以簡化成

(10)

其中

所以可以得到

(11)

因為E為負值，并且坐標系中z軸是朝上的，所以這里取負根號的結果。

雅可比矩陣的定義是末端執行機構速度與輸入關節速度的線性變換。當執行機構位于工作空間的任意位置的時候，它的矩陣元素會發生變化，它與時間存在一定的關聯。它的關系式為

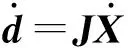
(12)

雅可比矩陣通常采用矢量積分和微分變換法求解，對于簡單的串聯機器人，通常采用微分變換法對方程求導，得到雅可比矩陣。對于復雜的并聯機器人，因為運動學方程求導過程復雜，所以通常通過矢量積法進行計算。本文采用矢量積法進行計算，即

(13)

式中Jd——逆向運動學雅可比矩陣Jx——正向運動雅可比矩陣J——雅可比矩陣

2 工作空間分析

2.1 奇異位形分析

對直線驅動并聯機器人的奇異行位進行分析，當雅可比矩陣的行列式為零時，并聯機械人出現奇異位形，對于式(13)而言，當Jd和Jx中任何一個或者2個矩陣行列式為零，會出現奇異位形。當矩陣Jd不可逆時，機器人出現逆向運動學奇異，當Jx不可逆時，機器人出現正運動學奇異，當矩陣Jd和Jx同時不可逆時，機器人出現組合奇異。下面對3種奇異位形進行討論：

(1)正向運動學奇異

當此類奇異位形時，數學上求解方程det(Jx)=0并找出所有點是很困難的，可以通過幾何關系較為直觀地找出所有的奇異位形點。將矩陣Jx看作3個向量，即

(14)

分別提取矩陣Jx的各行，發現各行向量分別對應從動桿l在基坐標系中的空間矢量。

從空間矢量的角度分析機構出現正向奇異性有以下兩種可能：①e1、e2、e33個向量均線性相關，這時候會出現共面情況，此時det(Jx)=0，3個矢量的Z分量都為0，動平臺與靜平臺重合，由機構可知不能達到，所以不用考慮，如圖4所示。②e1、e2、e33個向量中有3個向量線性相關，如圖5所示，此時3個桿件平行，這種情況在結構設計上無法避免，但是可以通過改變驅動電缸與靜平臺的角度來避免。

圖4 三矢量共面圖Fig.4 Three coplanar vector figure

圖5 兩矢量共線圖Fig.5 Two collinear vector figure

(2)逆向運動學奇異

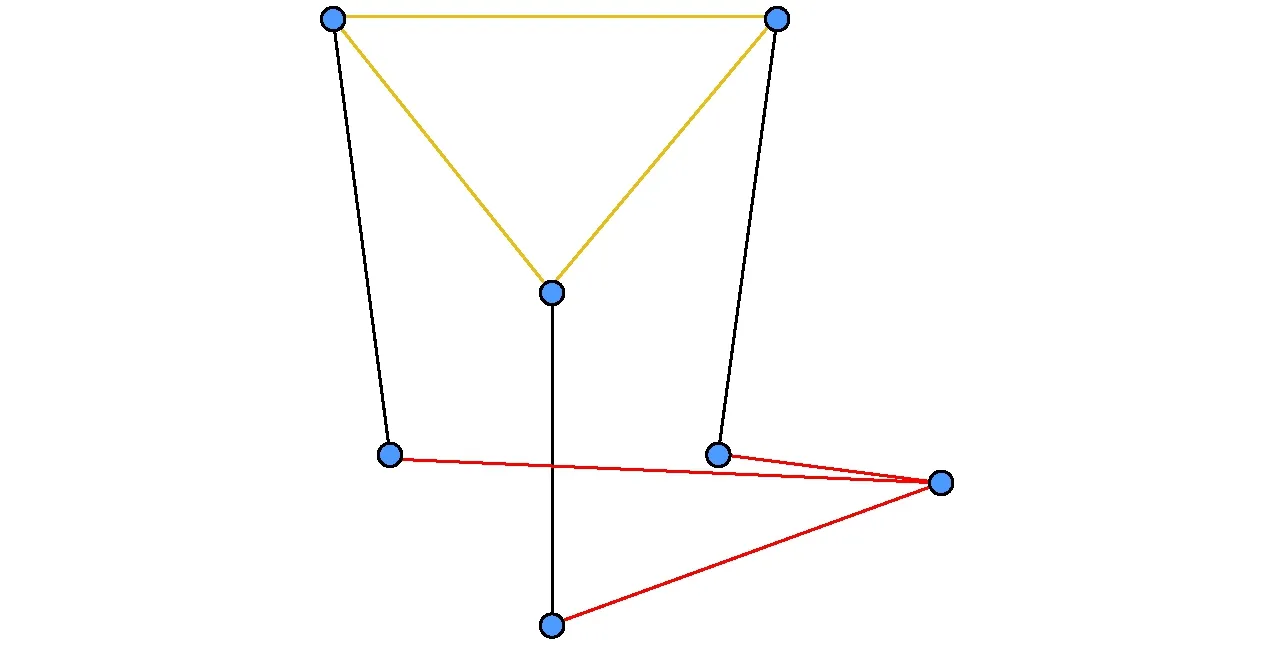
圖6 矢量垂直圖Fig.6 Vertical vector figure

(3)組合奇異

這種奇異狀態從公式上體現就是Jd和Jx同時不可逆，從前面的分析已經得到Jd不可逆的情況在直線驅動并聯機器人的機構中并不適用。所以同時出現的組合奇異在此結構中不存在。

2.2 虎克鉸約束分析

虎克鉸第1自由度的旋轉副沒有角度限制，可以360°旋轉，旋轉的速度向量與向量n1同向，n1是平面1的法向量，平面2與平面1垂直，法向量是n2；第2自由度的旋轉副有角度限制，它的旋轉速度向量始終在平面1內。如圖7所示，因為虎克鉸的第一自由度的旋轉副沒有角度的約束，所以虎克鉸約束來自于第2自由度的旋轉副，根據結構特點，第2旋轉副的旋轉關于平面1對稱，設桿件FiBi與平面1的夾角為γi1，桿件FiBi與平面2的夾角為γi2。如圖8所示，根據結構特點與幾何關系可知γi2沒有角度約束，所以可以得到γi1的角度約束關系為

(15)

根據實際的限制可知，-40°≤γi1≤40°，這樣可以得出工作空間的范圍。

圖7 平面法向量1和法向量2Fig.7 Normal vectors of plane 1 and plane 2

圖8 虎克鉸角度示意圖Fig.8 Diagram of Hooke hinge angle

2.3 工作空間求解

為了得到并聯機器人的工作空間，本文提出一種極坐標變步長迭代搜索法，其流程圖如圖9所示，具體的工作空間邊界搜索法步驟如下：

(1)通過式(8)和滑塊移動副的限制條件確定工作空間的最高點zmax和最低點zmin，并用一系列平行于OXY坐標面的平面將機器人可達工作空間均勻地分割成厚度為Δz的n個子空間，沿著z軸方向進行搜索。

(2)在第i個子空間中，極角從0遞增Δθ到2π，極徑從初值0開始以固定步長Δρ(稍大)遞增到ρ進行搜索。

(3)假設極徑遞增到第k次，若通過逆解算法求解出的滑塊移動副位置由滿足條件到不滿足條件，則令ρ(k)←ρ(k)-Δρ，Δρ←0.5Δρ，ρ(k+1)←ρ(k)+Δρ；否則ρ(k+1)←ρ(k)+Δρ。

(4)重復步驟(3)，若Δρ≤ε(ε為設定的極徑步長精度，ε=0.5 mm)且滑塊移動副的位置不滿足滑塊移動副的限制條件，此時，找到相應極角下的邊界點((ρ(k)+2Δρ)zicosθ,(ρ(k)+2Δρ)zisinθ,zi)。

(5)將所有子空間內的邊界點搜索出來，然后利用這些點生成并聯機器人的工作空間。

圖9 極坐標變步長迭代搜索法流程圖Fig.9 Program flow chart of polar coordinate variable step iterative search method

通過上面5個步驟，找出構成工作空間外輪廓的所有點，利用Matlab可視化功能，得到圖10所示的工作空間。

圖10 工作空間的Matlab仿真圖Fig.10 Diagram of Matlab simulation

2.4 結構參數對工作空間的影響

研究并聯機器人工作空間的尺寸與形狀對于提高并聯機器人的應用。本節重點針對直線驅動型并聯機器人的傾斜角、靜平臺與動平臺尺寸、滑塊高度等結構參數對進行分析。

由圖3可知，并聯機器人的結構參數主要包括靜平臺尺寸a、動平臺尺寸b、3個從動桿的桿長l、驅動器與靜平臺傾斜角α、滑塊高度h。為了得到當一個或多個參數變動時結果的表現，針對上面那些設計參數進行參數對工作空間的變化，虎克鉸角度的約束范圍是±40°，桿長l的初始長度是610 mm，讓桿長在510 mm到760 mm之間，以50 mm的增量進行變化。靜平臺邊長a的設計值是1 300.41 mm，讓它在1 000.41 mm到1 700.41 mm之間以100 mm的增量進行變化。動平臺的邊長初始值是103.923 mm。傾斜角α的初始值是38°，讓它在25°到90°之間以10°為增量進行變化。滑塊高度初始值是98.5 mm，讓它在78.5 mm到118.5 mm之間以10 mm為增量進行變化。

工作空間體積也可以定量計算出，如圖9所示，當θz增加Δθz的時候，相應的單位工作空間的體積可以表示成

(16)

對式(16)進行積分，可得整個工作空間的體積，表示為

(17)

式(17)可以通過Matlab進行計算求解。

圖11 工作空間體積與傾斜角度的關系Fig.11 Relationships of workspace volume vs actuators layout angle

由圖11可以看出，驅動器與靜平臺的傾斜角是一個開口朝下的拋物線，最高點在52°附近，在52°左側時，體積單調上升。當過了52°時，體積又單調減小，所以選在52°附近時，并聯機器人的體積最大。并且不會影響機器人占空間的大小。

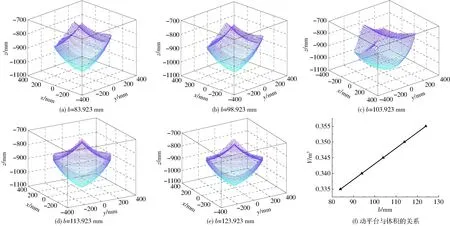
圖12 工作空間體積與動平臺邊長的關系Fig.12 Relationships of workspace volume vs size of moving platform

圖12反映了工作空間與動平臺邊長之間的關系，從圖12可以看出，動平臺的尺寸對整個機器人的工作空間的形狀影響不大，沒有出現奇異位置，所以都是合格尺寸。圖12還可以看出，動平臺邊長越大，體積越大，并且呈線性關系，但是，隨著邊長的擴大，下端的動平臺體積也會擴大，對工作環境的要求也就越高，因此不能作為結構參數的首選影響因素。

圖13 工作空間形狀與靜平臺邊長的關系Fig.13 Relationships of workspace shape vs the size of fixed platform

從圖13可以看出，工作空間的形狀與靜平臺存在很大關系的，靜平臺的邊長尺寸過大或者過小都會導致形狀變形，也會出現奇異，如圖13所示，此時因為靜平臺邊長太小，與動平臺邊長接近，所以圖像上方出現奇異狀態，并且圖像變形嚴重，當邊長過大時，整個圖像會出現上方拉長，下方變大，且奇異區域變多的情況。

每個結構參數對工作空間都有影響，靜平臺邊長與驅動器的傾斜角還有桿長對機器人工作空間的幾何形狀影響很大。其中靜平臺邊長過大或者過小都會導致幾何形狀出現變化，甚至會有死點等，所以在選擇靜平臺邊長尺寸時，需注意避免過大或者過小，隨著邊長的增加，體積越大。傾斜角對空間的高度影響很大，隨著角度的增加，工作空間的可達高度會變小，空間大小先增加后減小，當達到52°左右時達到最大。在實際運用中，需要根據需要工作空間的大小來選擇合適的結構參數，不同參數會導致機器人體積大小的變化，在生產線上，需要在滿足任務工作空間的情況下，使機器人占用體積越小，而不是單純的考慮工作空間的大小。

3 結構參數優化

由直線驅動型并聯機器人各機械結構參數對工作空間的影響分析可知，結構參數直接影響到工作空間的大小和形狀，因此，有必要對機器人結構參數進行優化，使得其在工作空間內的操作性能更優[15-17]。

3.1 優化模型

為了使優化后的結構參數既能滿足給定設計空間的需求，又能使并聯機器人的整體外形尺寸盡量小，以及其操作性能更優，定義了一個同時兼顧其操作性能和空間利用率的目標函數

(18)

其中

κ=cond(J)=‖J‖‖J-1‖

式中ω——權重系數(0≤ω≤1)V′——給定設計空間κ——雅可比矩陣的條件數，用來評價并聯機器人的操作性能

V*——機器人的可達工作空間

由于雅可比矩陣隨著機器人的位形變化而變化，所以用τ衡量機器人在給設計空間中的操作性能，直線驅動型并聯機器人結構參數優化可歸結為：給定設計空間(設計空間為400 mm×400 mm×100 mm的長方體)，確定靜平臺邊長a，滑塊高度h，從動桿桿長L，電缸與靜平臺之間的夾角α，動平臺邊長b，使得其空間利用率盡量大和操作性能更優。優化時，各結構參數的變化范圍根據文章第3部分各結構參數對應的三維工作空間圖和結構參數與體積的關系曲線圖確定；此外，必須考慮的約束條件有3支電缸上滑塊行程si和虎克鉸轉角Ui。

由于雅可比矩陣條件數κ越小，表示機器人的操作性能越好，而γ表示空間利用率是越大越好，為了統一，目標函數中取κ的倒數，所以優化的數學模型為

(19)

3.2 優化結果

本文優化算法選擇粒子群算法，該算法與諸如遺傳算法之類的算法相比，在進化過程中同時記憶位置和速度信息，另外，由于全局最優粒子提供信息給其他的粒子，整個搜索更新過程是跟隨當前最優解的過程，因此所有的粒子很可能更快地收斂于最優解。

利用Matlab粒子群優化算法工具箱(PSOt)，對上述數學模型進行求解，其中，根據機器人的實際應用需求，優化求解時， 將權重系數ω分別設置為0、0.5、1等3種情況，結果如表1所示。

從表1可知，ω為0時，即空間利用率最大，ω為1時，即機器人操作性能最優，圖14表示了操作性能最優的主視圖；圖15表示空間利用率最大的仿真圖。

表1 優化結果Tab.1 Numerical results of optimization

圖14 最優操作性能仿真圖Fig.14 Simulation diagram of the best dexterity

圖15 最大空間利用率仿真圖Fig.15 Simulation diagram of the best space utility

由圖14可以看出，操作性能最優時，長方體占任務工作空間的比重小于最大空間利用率，但是俯視圖可以看出長方體邊界離工作空間邊界較遠，運動學性能較優；圖15可以看出最大空間利用率的情況時，長方體邊界與任務空間邊界相交，運動學性能較差。

可以看出不同權重下優化函數指標模型是正確的，根據不同的實際需要，可以選擇不同的權重進行參數的篩選。

4 試驗驗證

為了驗證工作空間理論模型的正確性，對直線驅動型并聯機器人進行工作空間掃描試驗[18-20]。實驗所用測試平臺如圖16所示，采用FARO公司激光跟蹤儀Vantage(測試精度為0.015 mm)和相應的輔助裝夾設備來實時測量動平臺中心的位置。工作空間掃描方式如下：以機器人零點所在的z平面為起始平面，激光跟蹤儀分別以x、y軸運動5 mm為一個步長記錄下每個點的位置坐標，掃面完一個平面后，z坐標遞增20 mm，直至將整個工作空間掃描完成。將每個平面的邊界點取出來進行三維空間繪制，結果如圖17所示。

圖16 機器人工作空間掃描試驗現場Fig.16 Scene picture of workspace scan

將圖17與工作空間輪廓圖10進行對比，外觀形狀基本吻合，為了進一步地驗證，分別取出z=950 mm對應的平面邊界點的試驗數據和理論數據放一起進行對比，如圖18所示，試驗和理論數據構成的平面大小、形狀基本一致。試驗結果表明了工作空間理論模型是正確的，本文基于工作空間理論模型進行的各結構參數對工作空間的影響和結構參數優化的研究是正確的。

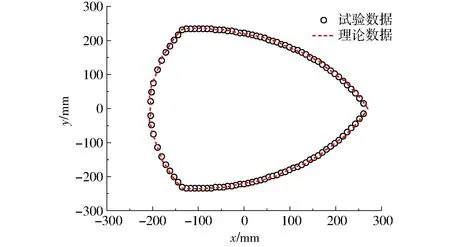
圖18 z=950 mm試驗和理論數據對比Fig.18 Comparison of theory and test data of z=950 mm plane

5 結論

(1)根據直線驅動型并聯機器人的幾何模型，利用矢量法建立其運動學模型，并得出機器人運動學逆解和雅可比矩陣。

(2)分析了奇異性和虎克鉸對工作空間的約束，提出一種極坐標變步長迭代搜索法求解出機器人的工作空間，并研究得到機器人各結構參數對工作空間的大小和形狀的影響趨勢。

(3)提出了一種綜合機器人靈巧度和空間利用率的全局混合性能指標，建立機器人結構參數優化數學模型，利用粒子群算法對其進行求解，得到不同工況下基于機器人靈巧度和工作空間利用率的最優參數，通過對不同權重下優化得到的參數進行仿真試驗，驗證了目標函數的正確性和有效性。

(4)將試驗掃描出的工作空間輪廓圖和理論模型求解出的工作空間輪廓圖進行對比，結果表明，工作空間理論模型是正確的，基于工作空間理論模型進行的各結構參數對工作空間的影響和結構參數優化是正確的，為后續的尺度綜合研究打下基礎。

1 馮李航，張為公，龔宗洋，等. Delta系列并聯機器人研究進展與現狀[J].機器人，2014,36(3):375-384. FEN Lihang，ZHNAG Weigong，GONG Zongyang，et al. Developments of delta-like parallel manipulators—a review[J]. Robot，2014,36(3):375-384. (in Chinese)

2 BOURI M, CLAVEL R. The linear Delta: developments and applications[C]∥The 41st International Symposium on Robotics, 2010: 1198-1205.

3 JO D Y. Workspace analysis of closed loop mechanisms with unilateral constraints[J].Adv in Des.Automat,1989,3:53-60.

4 GOSSELIN C M. Determination of the workspace of 6·DOF parallel mani Pula-tors[J]. ASME Journal of Mechanical Design,1990,112(3):331-336.

5 MERLET J P. Geometrical determination of workspace of a constrained parallel manipulators[J]. In: ARK, Frnace,1992:326-329.

6 MERLET J P. Determination of the orientation workspace of parallel manipula-tors[J]. Journal of lntelligent and Robotic Systems,1995, 13:143-160.

7 GOSSELIN C M, LAVOLE E, TOUTANT P.Robotics spatial mechanisms and mechanical systems[C]∥22nd Biennial Mechanisms Conference,1992:323-328.

8 MASORY O, WANG J. Workspace evalution of stewart platforms[C]∥22nd Biennial Mechanisms Conference,1992:337-346.

9 BONEY L A, RYU J. A new approach to orientation workspace analysi of 6-DOF parallel manipulators[J]. Mechanism and Machine Theory,2001,36(1):15-28.

10 REZAEI A, AKBARZADEH A, NIA P M, et al. Position, Jacobian and workspace analysis of a 3-PSP spatial parallel manipulator[J]. Robotics and Computer-Integrated Manufacturing, 2013, 29(4): 158-173.

11 YU M L, WANG J R, LI J, et al. Kinematics analysis of exoskeletons rehabilitation robot based on ADAMS[C]∥Advanced Materials Research. Trans Tech Publications, 2012, 479: 2333-2338.

12 HARADA T, DONG K, ITOIDAWA T. Design optimization of active scanning probe using parallel link mechanism [J]. International Journal of Precision Engineering and Manufacturing,2012,13(8): 1387-1394.

13 RUGBANI A, SCHREVE K. Modeling and analysis of the geometrical errors of a parallel manipulator micro-CMM[C]∥International Precision Assembly Seminar, 2012: 105-117.

14 崔國華,周海棟,王南,等. 基于Isight的3-UPS-S 并聯機器人機構多目標優化[J/OL].農業機械學報,2013,44(9):261-266. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20130945&journal_id=jcsam.DOI: 10.6041/j.issn.1000-1298.2013.09.045. CUI Guohua,ZHOU Haidong,WANG Nan, et al. Multi-objective optimization of 3-UPS-S parallel mechanism based on Isight[J/OL].Transactions of the Chinese Society for Agricultural Machinery,2013,44(9):261-266.(in Chinese)

15 ZHAO Y. Dimensional synthesis of a three translational degrees of freedom parallel robot while considering kinematic anisotropic property[J].Roboties and Computer-Integrated Manufacturing, 2013,29(1)：169-179.

16 梅江平,高奔,譚楊,等.3-SPR并聯機構運動學分析[J/OL].農業機械學報，2012,43(8):215-220. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20120839&journal_id=jcsam.DOI: 10.6041/j.issn.1000-1298.2012.08.039. MEI Jiangping, GAO Ben, TAN Yang, et al. Kinematic analysis of 3-SPR parallel mechanism [J/OL]. Transactions of the Chinese Society for Agricultural Machinery,2012，43(8):215-220. (in Chinese)

17 鐘琪, 劉貴杰, 王安憶,等. 移動副驅動的Delta機構工作空間分析及機構優化研究[J]. 機電工程, 2015, 32(11):1407-1411. ZHONG Qi, LIU Guijie, WANG Anyi, et al. Workspace resolution and mechanism optimization on Delta parallel mechanism driven by prismatic pair [J]. Journal of Mechanical and Electrical Engineering, 2015, 32(11):1407-1411.(in Chinese)

18 HARADA T, DONG K, ITOIGAWA T. Design optimization of active scanning probe using parallel link mechanism [J]. International Journal of Precision Engineering and Manufacturing, 2012,13(8): 1387-1394.

19 楊繼東,萬彪剛,高俊東,等.Tripod并聯機器人運動學分析與樣機實驗[J/OL].農業機械學報,2016,47(10):390-397. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20161051&journal_id=jcsam.DOI: 10.6041/j.issn.1000-1298.2016.10.051. YANG Jidong, WAN Biaogang, GAO Jundong, et al. Kinematic analysis and experiment of Tripod parallel robot[J/OL].Transactions of the Chinese Society for Agricultural Machinery,2016,47(10):390-397. (in Chinese)

20 余躍慶,崔忠煒,趙鑫,等.柔順關節并聯機器人設計與實驗[J/OL].農業機械學報,2013,44(7):274-278. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20130747&journal_id=jcsam.DOI:10.6041/j.issn.1000-1298.2013.07.047. YU Yueqing, CUI Zhongwei, ZHAO Xin, et al. Design and experiment of parallel robot with compliant joints[J/OL].Transactions of the Chinese Society for Agricultural Machinery,2013,44(7):274-278. (in Chinese)