應用稀疏約束的非負正則矩陣學習算法①

魏瑞芳,周棟森

(浙江郵電職業技術學院 教務處(科研處),紹興 312016)

子空間降維是機器學習和模式識別的一種常用方法,也是數據挖掘等領域的研究熱點.Lee和Seung[1]在《Nature》上首次提出非負矩陣分解(Non-negative Matrix Factorization,NMF)概念,通過添加“矩陣中所有元素均非負”限制條件,保證分解結果的可解釋性.隨后,大量改進算法被提出并應用.文獻[2]在分解原始矩陣時,對基矩陣和系數矩陣施加稀疏約束,將稀疏編碼思想引入到非負矩陣分解中,提出的稀疏約束非負矩陣分解算法(Non-negative Matrix Factorization Sparseness Constraints,NMFSC)具有存儲空間少的優點;文獻[3]將增量學習與非負矩陣分解相結合,提出了增量式非負矩陣分解算法(Incremental Non-negative Matrix Factorization,INMF),利用上一步的分解結果參與迭代運算,再新加入訓練樣本時不會重新運算從而節省了運算時間.文獻[4]將稀疏約束和增量學習思想引入非負矩陣分解中,提出的稀疏約束下非負矩陣分解的增量學習算法(Incremental Non-negative Matrix Factorization Sparseness Constraints,INMFSC)在運算時間和稀疏度等指標上都有大幅優化.上述的標準NMF及其改進算法都屬于無監督分解方法,沒有考慮樣本的標簽信息.文獻[6]將流形學習與非負矩陣分解相結合,提出的圖正則化非負矩陣分解(Graph Regularized Nonnegative Matrix Factorization,GNMF)能夠在NMF的低維表示中考慮原始樣本的近鄰結構,使得原始樣本的近鄰結構在非負矩陣分解的低維中得到很好的保留.文獻[7]提出了稀疏約束的圖正則非負矩陣分解,并給出了迭代公式以及收斂性證明過程.現有研究成果普遍存在非負矩陣分解數據稀疏性降低及訓練樣本增多導致運算規模不斷增大等現象.

針對現有非負矩陣分解后的數據稀疏性較低,訓練樣本偏多導致運算規模持續增大的普遍現象問題,本文將文獻[7]方法與學習算法融合提出基于稀疏約束的非負正則矩陣學習算法(Non-negative Factorization Matrix with Sparseness Constraints,NFM-SC),NFMSC方法不僅能夠有效保持樣本局部結構,使得算法具有較高分類準確率,還能結合學習算法充分利用上一步分解結果,避免重復計算從而達到降低運算時間目標.

1 非負矩陣分解

NMF算法具體描述如下[8-10]:對給定的非負矩陣V,尋找合適的非負基矩陣和非負系數矩陣,使得V≈WH.r代表基向量的個數,當r的取值滿足時,原始矩陣V得到了有效的壓縮.可歸結為最小化下面的歐式空間的描述形式的目標函數:

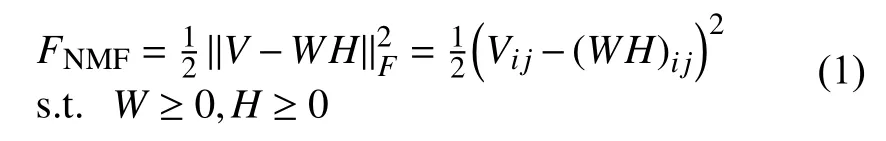
目標函數的乘性迭代規則為:

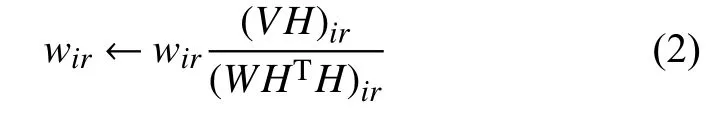
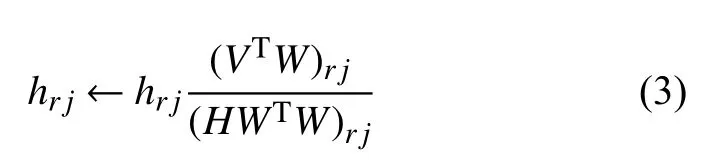
當給定迭代終止條件后,對隨機生成的初始非負矩陣W0和H0,按式(2)和(3)交替迭代更新直到滿足終止條件,可得到最終的W和H[11-13].

2 稀疏約束圖正則非負矩陣分解學習算法

文獻[7]提出的稀疏約束圖正則非負矩陣分解方法不僅考慮數據幾何結構,而且對稀疏矩陣進行約束,能夠提取既稀疏又具有很強判別能力的基圖像.本文將文獻[7]與學習算法融合提出基于稀疏約束的非負正則矩陣學習算法(Non-negative Factorization Matrix with Sparseness Constraints,NFM-SC),結合學習方法充分利用上一步的分解結果,避免大量重復計算過程.

2.1 目標函數

設Wk和Hk分別表示樣本集合Vk的非負矩陣分解后得到的基矩陣和系數矩陣,Lk是樣本集合Vk的拉普拉斯矩陣,其中k表示當前樣本集合中存在k個樣本.Fk代表Vk經過非負矩陣分解后的目標函數,則Fk的表達式如式(4)所示.

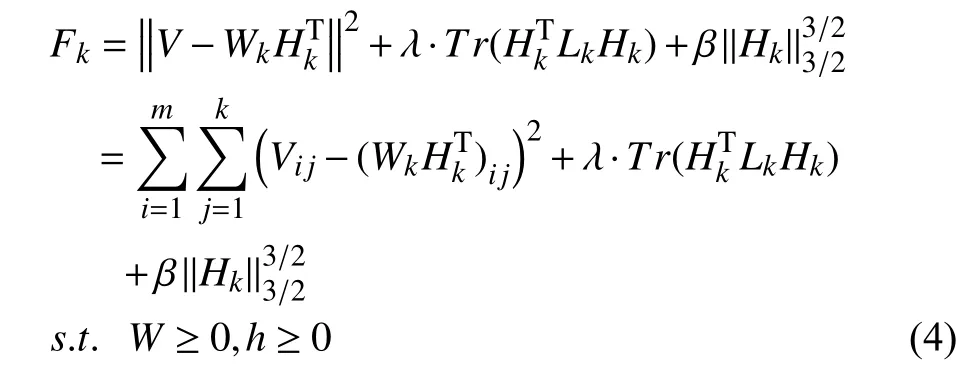
當第k+1個樣本加入后,目標函數則如式(5).

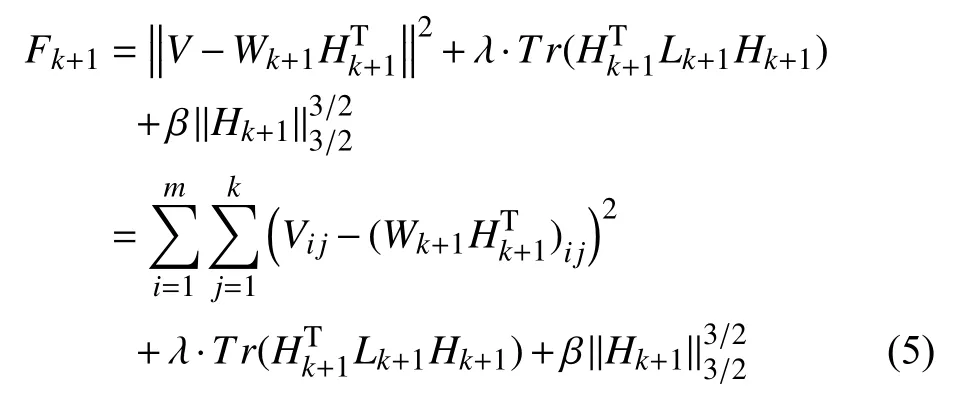
其中,β是非負參數,Wk+1和Hk+1分別表示樣本集合Vk+1非負矩陣分解后得到的值,Lk+1是樣本集合Vk+1的拉普拉斯矩陣.

2.2 迭代規則

當新樣本vk+1到來時,系數矩陣Hk+1的前k列向量近似等于Hk的列向量,即Hk+1=[Hk,hk+1].目標函數Fk+1可以重寫為如式(6)形式.

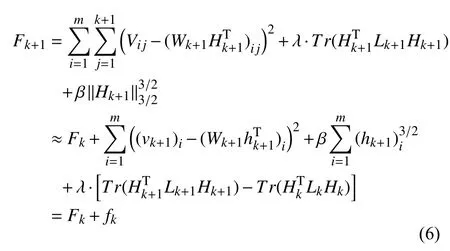
在得到新的目標函數Fk+1后,利用梯度下降法推導出相應的迭代公式.先求出系數矩陣增量部分hk+1的迭代公式,如式(7).

接下來計算Fk+1對hk+1的偏導數:

其中,(Lk+1)k+1,:、(Dk+1)k+1,:和(Sk+1)k+1,:分別為Lk+1、Dk+1和Sk+1所對應的第k+1行的行向量.

將式(8)和(9)的值代入式(7),得hk+1的迭代公式,如式(10).

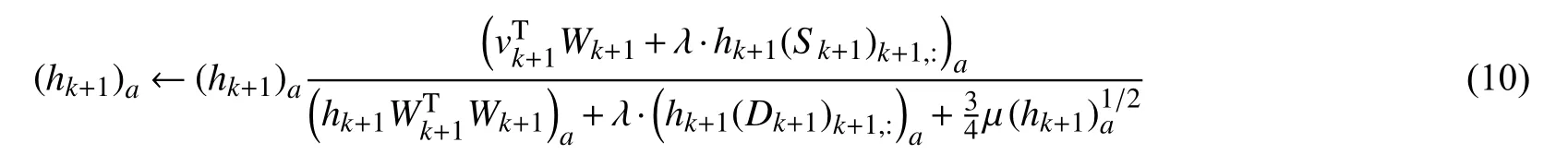
同理,得:

ηia是迭代的步長,

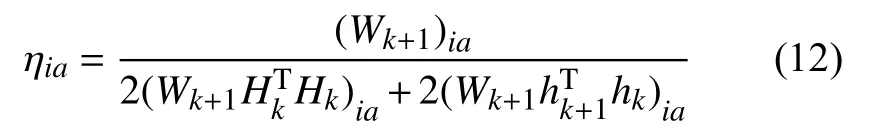
將公式(12)和(13)的值代入(10),得Wk+1的迭代公式:

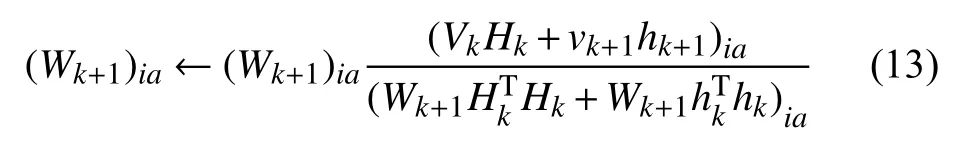
由此,歸納NFM-SC算法步驟如下:

(1)依據2.1小節目標函數內容,隨機初始化正則矩陣W和H;

(2)對訓練樣本集V(包含k個訓練樣本)按以下規則進行迭代運算,直至滿足收斂條件:

(3)當加入新訓練樣本vk+1時,按以下迭代規則更新W和H直至滿足收斂條件:

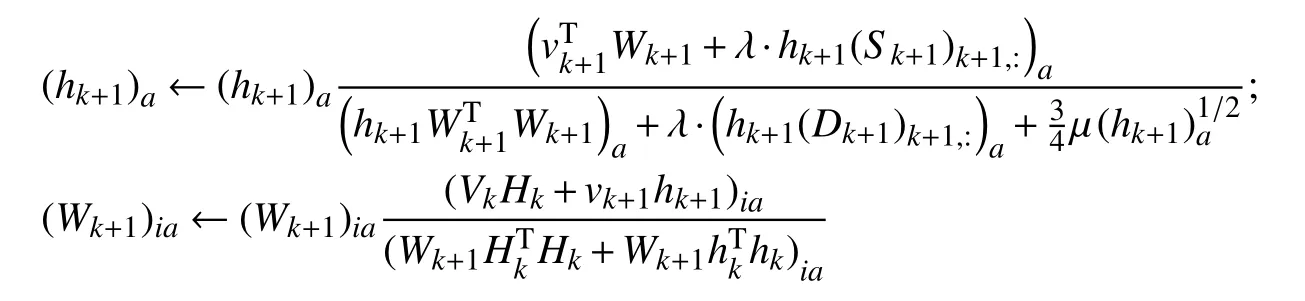
其中,Hk+1=[Hk,hk+1],hk+1初始化為hk.以上i=1,2,…,n,j=1,2,…,n,a=1,2,…,r,α和β均為非負常數.

3 實驗分析

實驗環境:Windows 7,CPU:3.30 GHz,內存:8 GB.程序環境:Matlab R2014b.

3.1 數據描述及參數設置

本實驗采用ORL人臉數據庫和COIL20圖像數據庫測試NFM-SC算法性能,并與NMF、INMF、GNMF、INMFSC四種算法進行比較.ORL人臉數據庫中包含40個不同年齡、不同性別和不同種族的面部圖像,每人10種不同姿態,共計400幅灰度圖像.COIL20數據庫共有20個類別的物體圖像,每個圖像包括具有不同旋轉角度的72個樣本.

在運行本文實驗算法時,在每個類取6個共240個作為訓練樣本,正則項參數λ設為100,稀疏約束β設為0.3,迭代次數為200.在每個類取43個共860個作訓練樣本,正則項參數λ設為100,稀疏約束β設為0.4,迭代次數為200次.

3.2 運行實踐對比

在ORL人臉數據庫上,初始訓練樣本為240的情況下NMF、INMF、GNMF、INMFSC及NFM-SC五種算法隨新增樣本數量的增多消耗的時間如表1所示,在COIL20數據集上初始訓練樣本為860的情況下算法時間消耗如表2所示.

表1 ORL庫新增訓練樣本時不同算法對應時間消耗(單位:s)

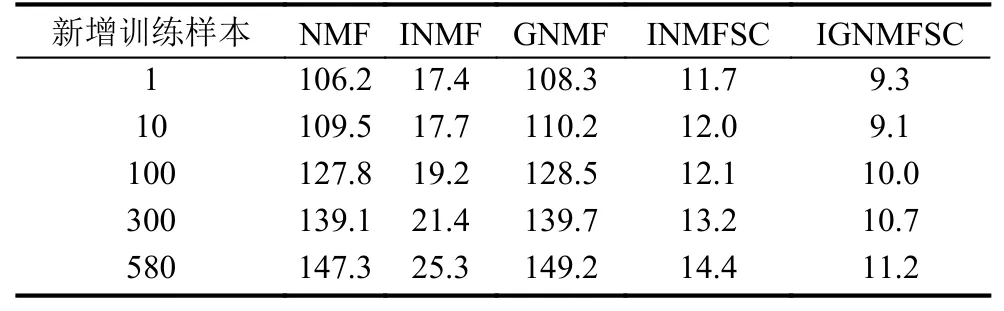
表2 COIL20庫新增訓練樣本時不同算法對應時間消耗(單位:s)

由表1和表2的結果可知,與幾種對比算法比較,提出的算法在運算的時間上有明顯優勢,而當新增訓練樣本超過一定數量時,NFM-SC算法仍能保持相對高的運算效率.

3.3 稀疏度的度量

度量稀疏度的函數為:

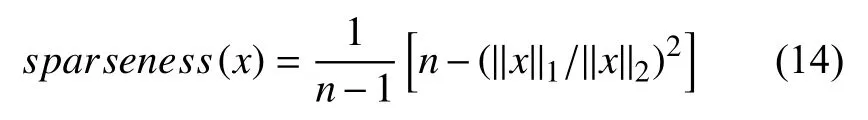
其中,n是向量x的維度,‖·‖1是向量的1范數,‖·‖2是向量的2范數,0≤sparseness(x)≤1.當x僅有一個非零元素時,函數值為1;當所有元素都不為零且相等時,函數值為0.

以式(14)作為稀疏度度量標準,則經過NMF、INMF、GNMFSC和本文提出的NFM-SC算法分解后得到的基矩陣W和系數矩陣H的稀疏度如表3所示.

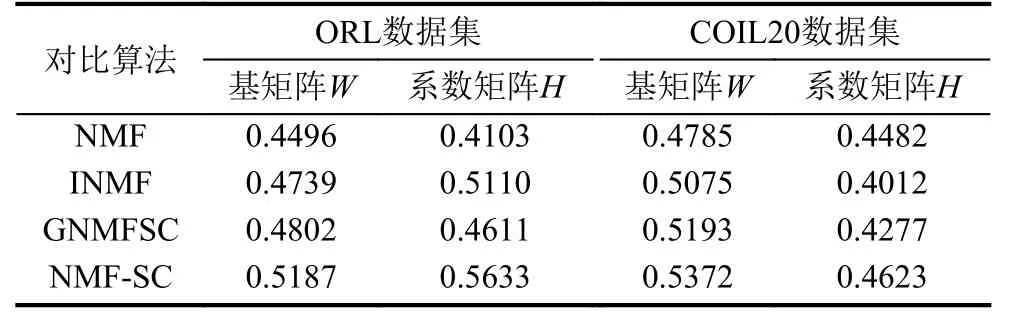
表3 幾種算法得到的因子矩陣稀疏度

圖1、圖2分別表示在數據庫ORL和COIL20上的基圖像.其中,ORL數據集的基矩陣特征維數取36,COIL20數據集的基矩陣特征維數取20.

圖1 COIL20數據集的基圖像(r = 20)

由圖1和圖2可以看出,NMF算法的基向量最接近原圖像,容易得到原始樣本的最優表示,但是它的稀疏度較差,存儲效率低.同其他的NMF改進算法相比,NFM-SC算法能得到更稀疏的基圖像,由此表明算法得到了圖像的最佳局部表示結果.

圖2 COIL20數據集的基圖像(r = 20)

4 結論

提出了稀疏約束的非負正則矩陣學習算法,并給出了相應的迭代規則和算法步驟.通過在常用數據集上幾種算法的對比實驗,綜合考慮運行時間和稀疏度兩種評價指標來衡量所提算法的有效性,實驗表明,提出的算法不僅縮減運行時間,而且使分解后的數據更為稀疏,得到局部表達能力和判別能力更強的基圖像.

1Lee DD,Seung HS.Learning the parts of objects by nonnegative matrix factorization.Nature,1999,401(6755):788-791.[doi:10.1038/44565]

2Hoyer PO.Non-negative matrix factorization with sparseness constraints.The Journal of Machine Learning Research,2004,5:1457-1469.

3Bucak SS,Gunsel B.Incremental subspace learning via nonnegative matrix factorization.Pattern Recognition,2009,42(5):788-797.[doi:10.1016/j.patcog.2008.09.002]

4王萬良,蔡競.稀疏約束下非負矩陣分解的增量學習算法.計算機科學,2014,41(8):241-244.[doi:10.11896/j.issn.1002-137X.2014.08.051]

5Liu CL.Classifier combination based on confidence transformation.Pattern Recognition,2005,38(1):11-28.[doi:10.1016/j.patcog.2004.05.013]

6Cai D,He XF,Han JW,et al.Graph regularized nonnegative matrix factorization for data representation.IEEE Transactions on Pattern Analysis and Machine Intelligence,2011,33(8):1548-1560.[doi:10.1109/TPAMI.2010.231]

7姜偉,李宏,于震國,等.稀疏約束圖正則非負矩陣分解.計算機科學,2013,40(1):218-220,256.

8李樂,章毓晉.非負矩陣分解算法綜述.電子學報,2008,36(4):737-743.

9姜小燕.基于非負矩陣分解的圖像分類算法研究[碩士學位論文].錦州:遼寧工業大學,2016.

10汪金濤,曹玉東,王梓寧,等.圖像型垃圾郵件監控系統研究與設計.遼寧工業大學學報(自然科學版),2016,36(2):78-80,86.

11胡學考,孫福明,李豪杰.基于稀疏約束的半監督非負矩陣分解算法.計算機科學,2015,42(7):280-284,304.[doi:10.11896/j.issn.1002-137X.2015.07.060]

12杜世強,石玉清,王維蘭,等.基于圖正則化的半監督非負矩陣分解.計算機工程與應用,2012,48(36):194-200.[doi:10.3778/j.issn.1002-8331.1205-0357]

13卜寧,牛樹梓,馬文靜,龍國平.面向相似App推薦的列表式多核相似性學習算法.計算機系統應用,2017,26(1):116-121.[doi:10.15888/j.cnki.csa.005502]