基于旋量理論的仿人機械臂正運動學與可操作性分析*

李文威 周廣兵,2 陳再勵 吳亮生 黃煒聰 陳惠綱

?

基于旋量理論的仿人機械臂正運動學與可操作性分析*

李文威1周廣兵1,2陳再勵1吳亮生1黃煒聰1陳惠綱1

（1.華南智能機器人創新研究院 2.廣東省智能制造研究所）

為研究仿人機械臂的運動性能，采用旋量理論對SRU構型仿人機械臂進行正運動學與可操作性分析。首先基于指數積公式對機械臂進行正運動學分析，獲得通用的正解解析式；其次基于運動旋量計算機械臂的雅克比矩陣，并通過雅克比矩陣獲得機械臂操作空間中任意一點的全局相對可操作度；最后以某六自由度仿人機械臂為算例，對該機械臂進行正運動學和可操作性分析，給出可視化計算結果。

仿人機械臂；旋量理論；正運動學；指數積；雅克比矩陣

0 引言

D-H參數法和基于旋量理論的指數積（product of exponential，POE）公式是機器人運動學分析的2種重要方法，并在機械臂的運動學分析中廣泛應用[1-2]。

D-H參數法需要針對每個桿件建立局部坐標系，然后在局部坐標系下，基于桿件的4個參數建立相鄰桿件間的位姿變換矩陣，繼而以首端到末端一系列變換矩陣的乘積表示機器人的末端位姿。D-H參數法建模過程復雜，當局部坐標系建立不恰當時，易產生奇異性；當自由度增多時，易形成累積誤差。

應用基于旋量理論的POE公式進行機械臂的正運動學分析，基本過程是：1）分別在機械臂的基座和末端建立基坐標系和工具坐標系；2）在基坐標系下，確定機器人的初始位姿、關節的位置向量和軸向量；3）將關節位置向量和軸向量變換為運動旋量；4）通過POE矩陣指數連乘形式表達機械臂的末端位姿。可見，機械臂末端位姿誤差只來源于位置向量和軸向量，可從根本上避免奇異性和累積誤差的產生。

采用旋量理論建立的機械臂運動學分析模型不僅具有形式統一、描述簡潔的優點，并且可應用在更深入的理論分析中，如，蘭陟等采用旋量理論計算了五自由度機械臂的雅克比矩陣[3]；Zhu S等采用旋量理論對串聯機械臂進行了動力學分析[4]。

1 正運動學分析

正運動學分析是給定各關節角，求機械臂末端位姿的一類問題。一種六自由度仿人機械臂的初始位姿狀態及其結構參數如圖1所示。該機械臂具有類似人臂的SRU（球面副-轉動副-萬向節副）串聯構型，其構型特點為：1）前3個自由度正交于一點，其肩關節等效于一個球面副（S）；2）肘關節為轉動副（R），只有1個自由度；3）后2個自由度正交于一點，其腕關節等效于一個萬向節副（U）。這種具有類似人臂結構特征的仿人機械臂能夠較好地模擬人臂運動[5]。

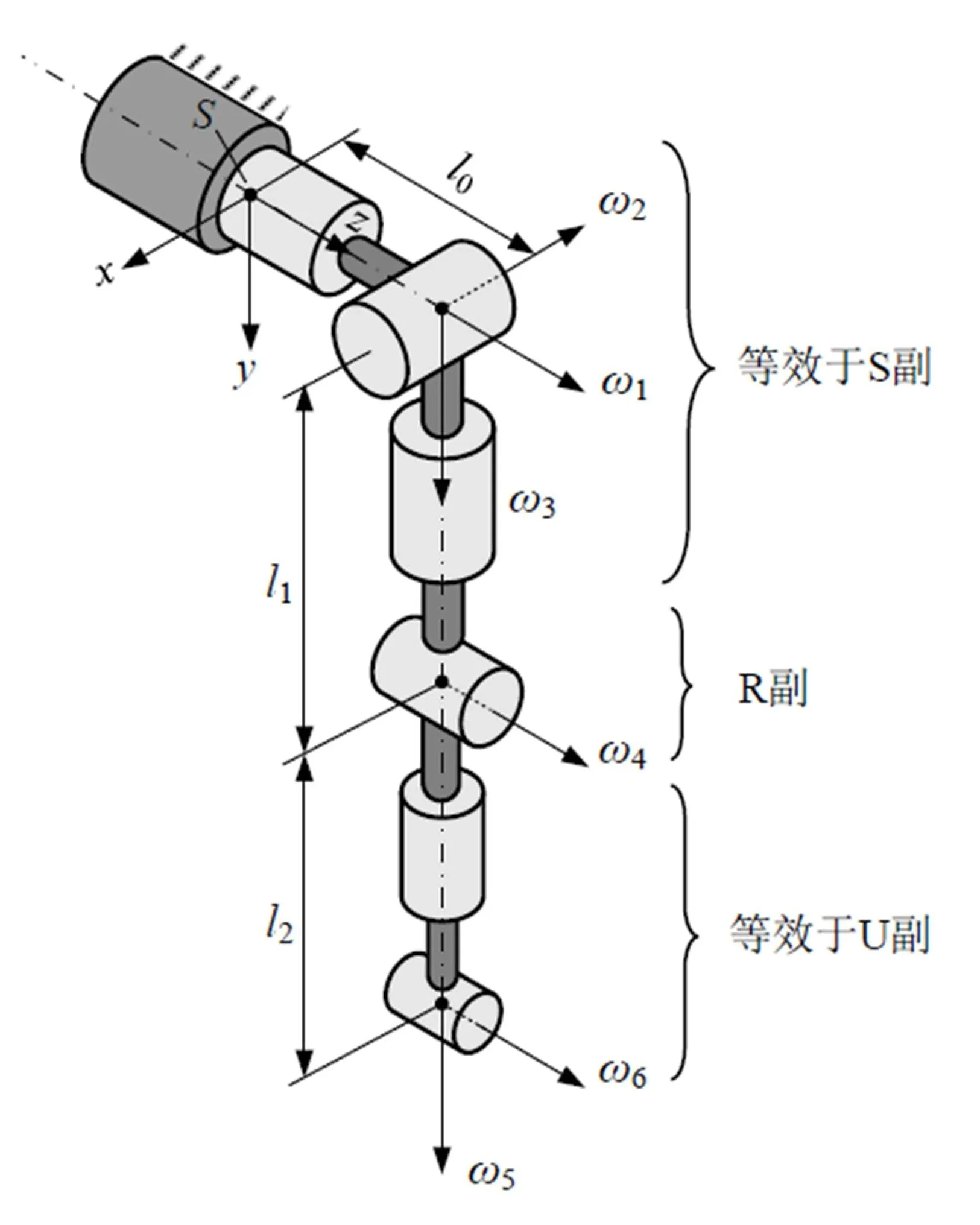
圖1 SRU構型仿人機械臂的結構參數

在圖1的基坐標系下，機械臂末端的初始位姿齊次矩陣為

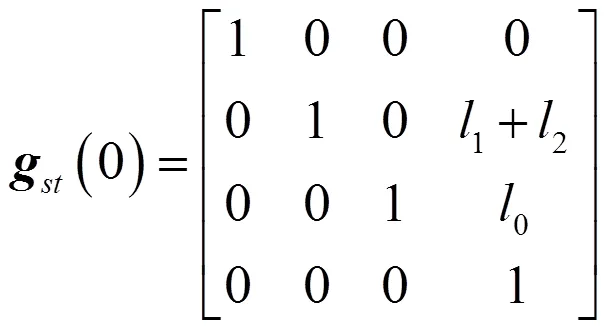
按圖1所示位置，計算各自由度的運動旋量坐標，所得結果整理后列于表1中。

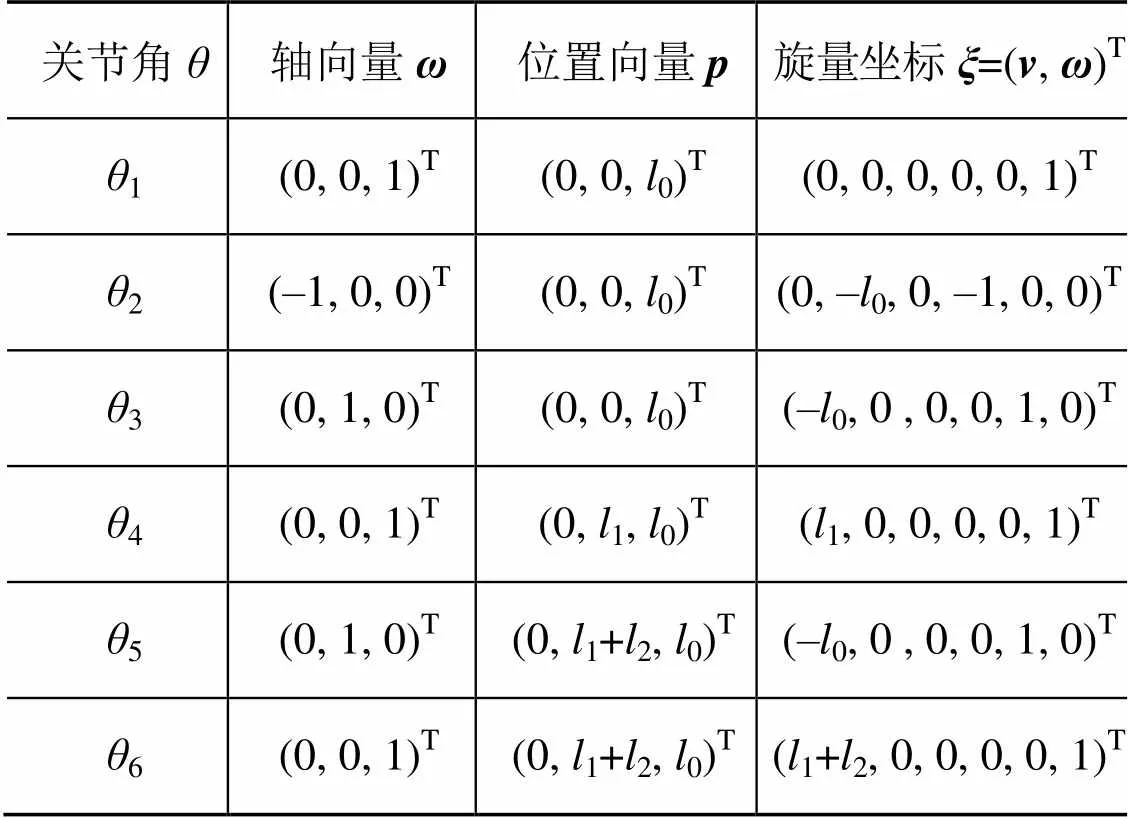
表1 各自由度的運動旋量坐標

將機械臂各自由度的運動旋量坐標表示為

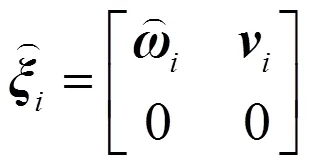
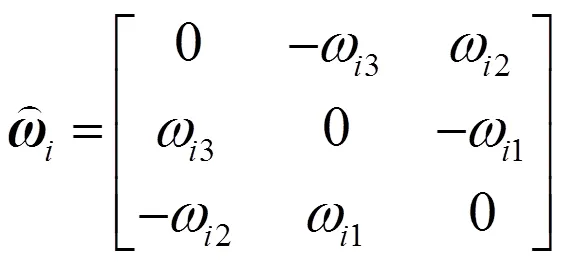
根據旋量的POE原理，目標位姿為

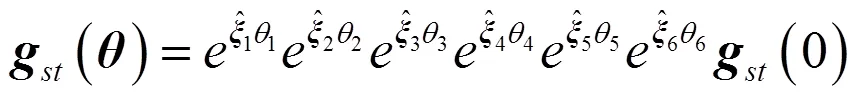
根據指數映射關系

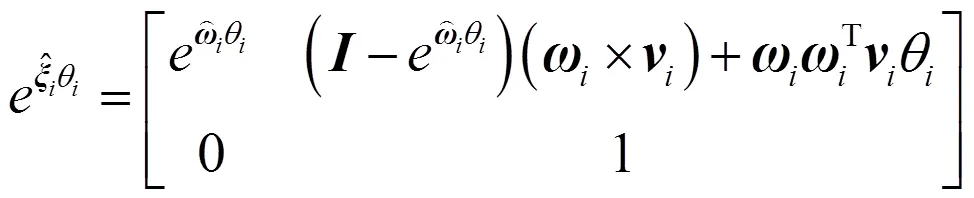
可計算得到運動學正解計算式為

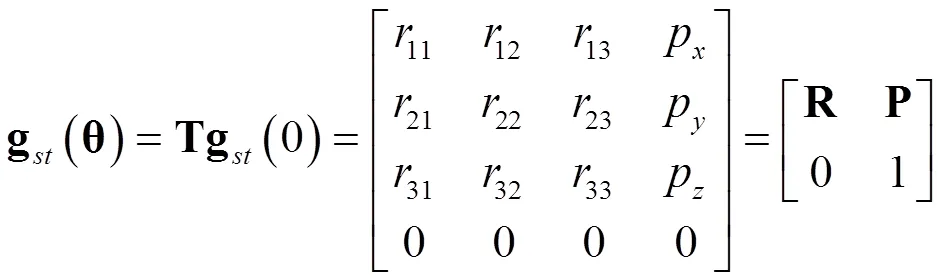
以符號運算形式在Matlab中編寫運動學正解計算程序，得到式(5)中各元素的解析式為

11=6{5[4(13+123) –214] –5(13–

312)} –6[4(13+123) +241]

12= –6[4(13+123) +241] –

6{5[4(13+123) –214] –

5(13–312)}

13=5[4(13+123) –214] +

5(13–312)

21=6{5[4(31–123) +124] –5(13+

132)} –6[4(31–123) –124]

22= –6[4(31–123) –124] –

6{5[4(31–123) +124] –

5(13+132)}

23=5[4(31–123) +124] +

5(13+132)

31= –6[5(24+243) +235] –

6(42–234)

32=6[5(24+243) +235] –

6(42–234)

33=235–5(24+243)

p= –121–2241–2134–21234

p=112+2124–2314+21234

p=0–12–242+2234

其中，C= cosθ；S= sinθ。

2 可操作性分析

對于機器人來說，可操作性反映了整個系統對力和運動的全局轉換能力，也就是機器人在任意方向上的運動和施加力的能力[6]。

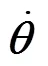
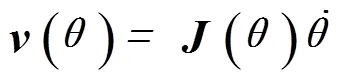
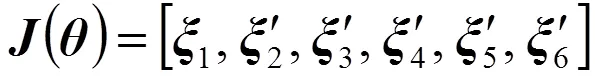
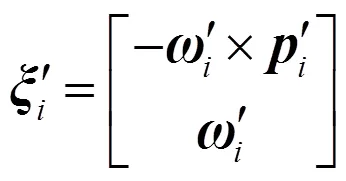
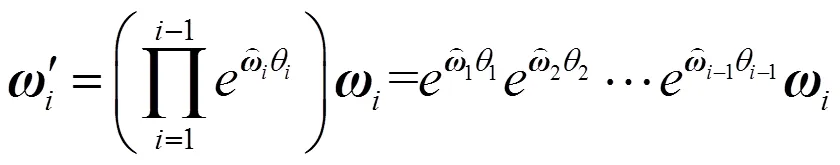
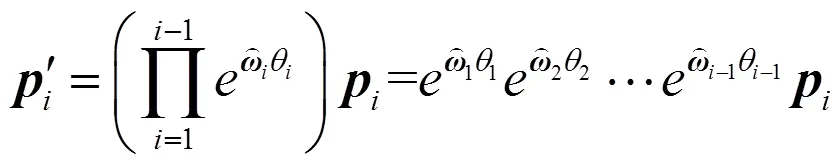
以求出的雅克比矩陣為基礎，可進一步求得經過歸一化處理的空間點全局相對可操作度[5]：

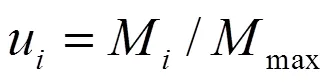
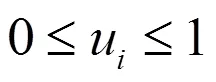
3 算例

為檢驗本文推導的運動學正解和可操作度計算式的正確性，以結構參數為(0,1,2)T= (0.15 m, 0.25 m, 0.25 m)T的仿人機械臂為實際算例進行驗證。

首先，以特殊位姿驗證正運動學分析結果的正確性。給定一組關節角(1,2,3,4,5,6)T= (0, 0, 0,–π/2, 0, 0)T，根據式(5)可計算得到末端位姿為

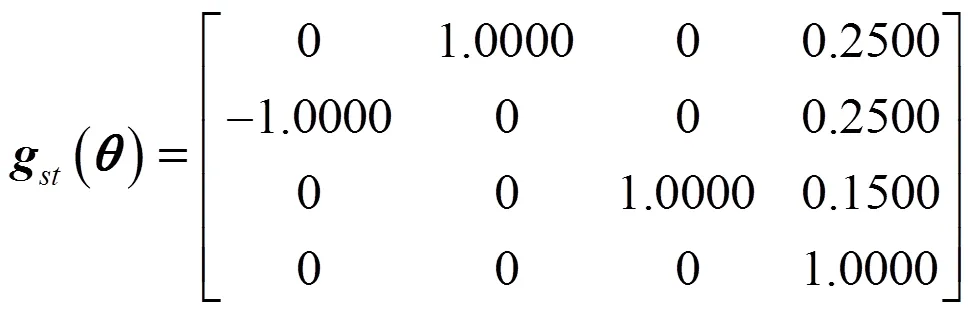
與式(13)對應的機械臂位姿的仿真效果如圖2所示，可見，該位姿與機器人的實際末端位姿一致，說明正解計算正確。

采用蒙特卡洛法隨機抽取機械臂關節空間內10000個點；再根據正運動學計算式(5)求出機械臂操作空間內相對應的10000個空間點坐標；最后利用式(7)~式(12)求出各空間點對應的全局相對可操作度值。經計算，機械臂工作空間內可操作度的最大值max= 0.0372。

為使機械臂操作空間內的全局相對可操作度的分布以可視化的方式呈現，在每個空間點位放置一個小圓球，并以圓球的直徑代表u值的大小，所得機械臂操作空間內的可操作性分布如圖3所示。由圖3可見，機械臂的操作空間大致呈橢球型，橢球的外表面、中心點及上下頂點等極限位置附近可操作性較差。表2列出了機械臂操作空間內若干點位的全局相對可操作度數值。

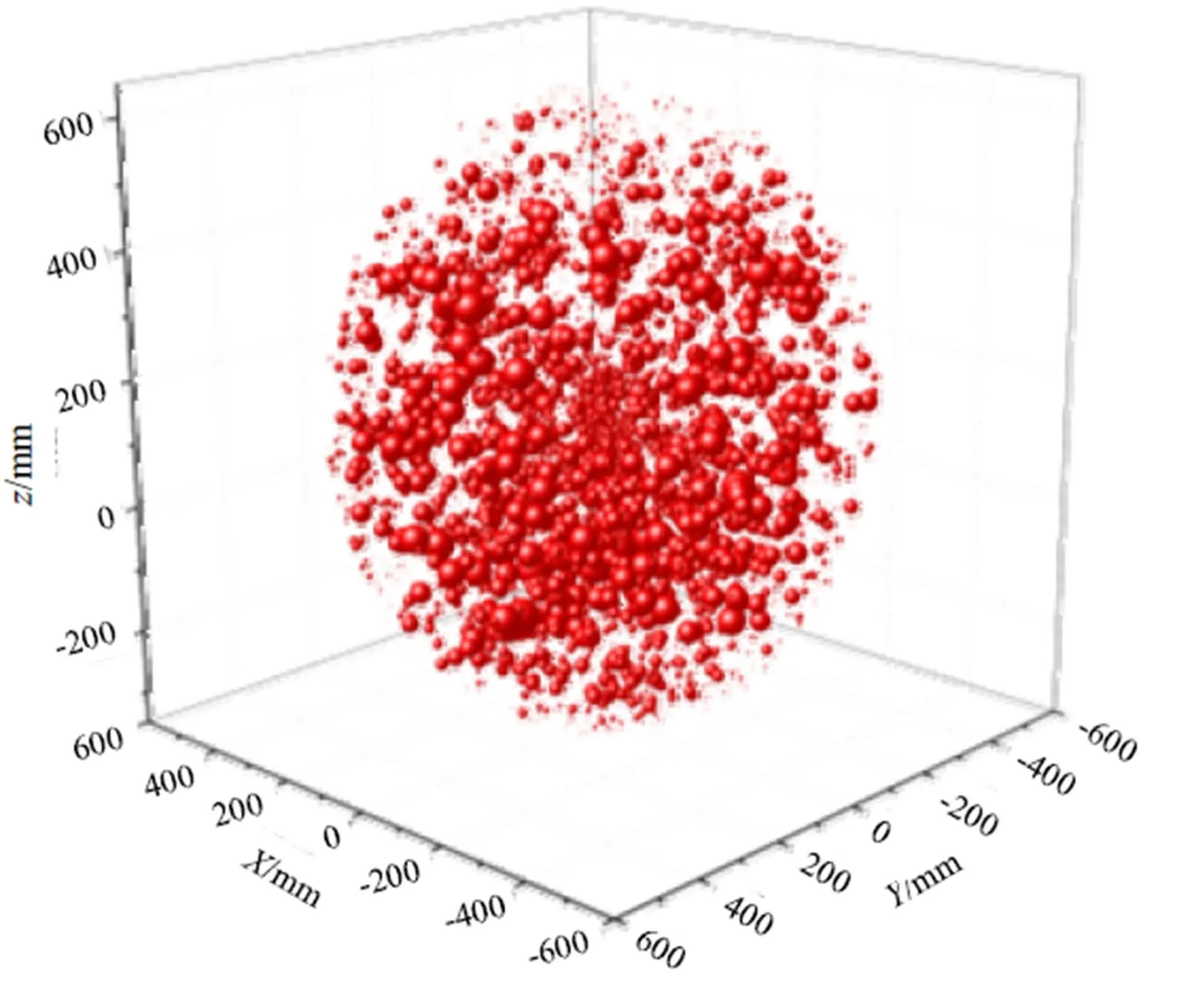
圖3 機械臂操作空間內的可操作性分布

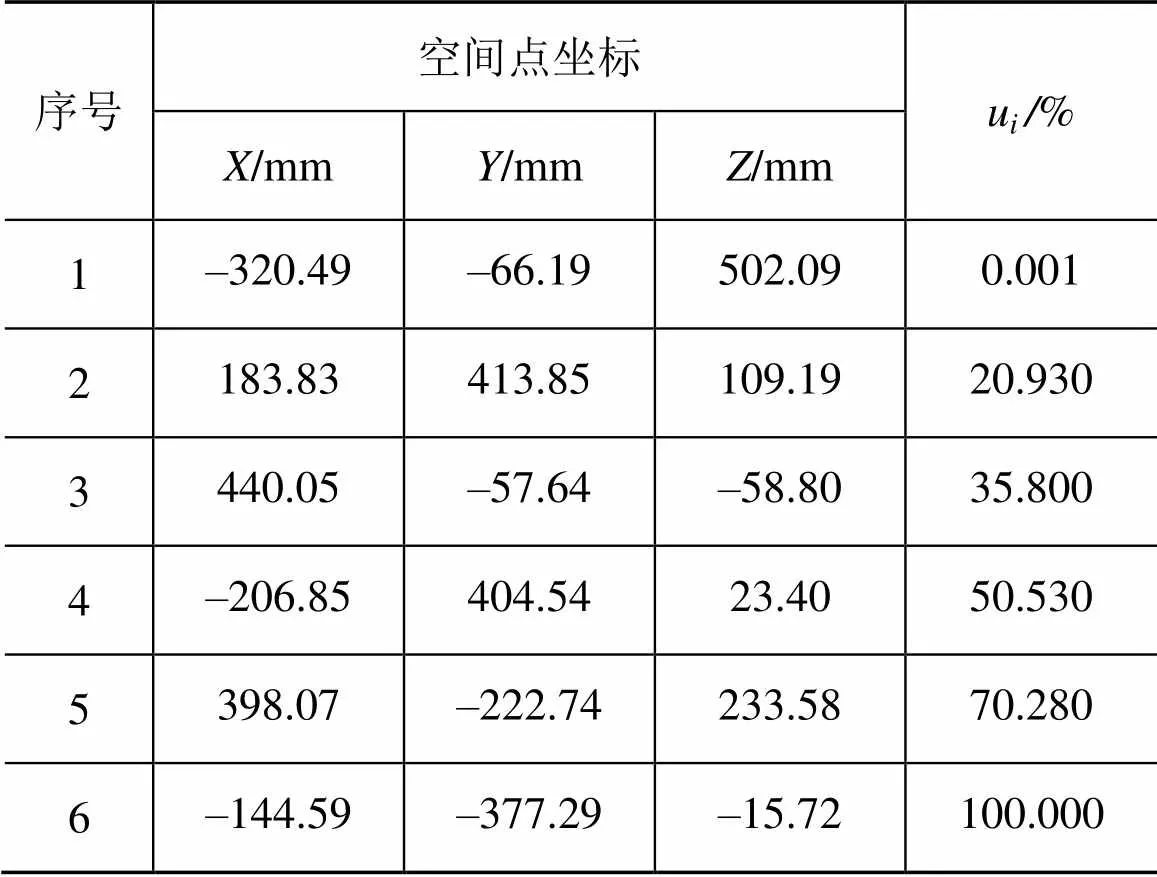
表2 機械臂操作空間內若干點位的全局相對可操作度

4 結語

基于旋量理論研究機械臂的運動性能，具有幾何意義明確、表達形式統一和編程計算簡便等優勢。本文基于旋量理論推導了SRU構型仿人機械臂的運動學正解與全局相對可操作度的解析計算式，并針對一給定尺寸參數的六自由度仿人機械臂進行了相應的數值計算，文中的計算過程與所得結論對相似構型機械臂的運動性能分析具有一定的參考意義。后續將進一步研究運動旋量中包含隨機誤差時，仿人機械臂運動學性能的變化規律，并據此分析影響機械臂運動精度的關鍵因素。

[1] 朱齊丹,王欣璐.六自由度機械臂逆運動學算法[J].機器人技術與應用,2014(2):12-18.

[2] Kevin M L, Frank C P. Modern robotics: mechanics, planning, and control[M]. Cambridge: Cambridge University Press, 2017.

[3] 蘭陟,李振亮,李亞.基于旋量理論的5-DOF上肢康復機器人雅克比矩陣求解[J].機械設計,2011,28(5):51-53,74.

[4] Zhu S, Chen Q, Wang X, et al. Dynamic?modelling using?screw theory?and nonlinear sliding mode control of serial robot[J]. International Journal of Robotics and Automation, 2016, 31(1): 63-75.

[5] 趙京,宋春雨,杜濱.基于人體工程學的仿人機械臂構型[J].機械工程學報,2013,49(11):16-21.

[6] 劉迎春,余躍慶,姜春福.機器人可操作性研究進展[J].機械設計與研究,2003,19(4):34-37,7.

Forward Kinematics and Maneuverability Analysis of Humanoid Arm Based on Screw Theory

Li Wenwei1Zhou Guangbing1,2Chen Zaili1Wu Liangsheng1Huang Weicong1Chen Huigang1

(1.South China Robotics Innovation Research Institute 2.Guangdong Institute of Intelligent Manufacturing)

In order to analyze the motion performance of the humanoid arm, the forward kinematics and maneuverability analysis of the SRU humanoid arm were carried out by means of screw theory. Firstly, the forward kinematics of the arm was analyzed based on the product of exponential formula, and the general analytical formula of the forward kinematics solution was obtained. Secondly, the Jacobian matrix of the arm was calculated based on the motion screws, and the global relative maneuverability of any point in the operating space was derived by the Jacobian matrix. Finally, the forward kinematics and maneuverability of a humanoid arm with six degrees of freedom were analyzed, and the visualization results were given.

Humanoid Arm; Screw Theory; Forward Kinematics; Product of Exponential; Jacobian Matrix

李文威，男，1981年生，博士，助理研究員，主要研究方向：智能機器人、CAE仿真與優化、機械動力學。E-mail: liwenwei011@163.com

周廣兵，男，1984年生，碩士，工程師，主要研究方向：智能服務機器人、智能制造裝備。

陳再勵，男，1989年生，碩士，工程師，主要研究方向：機器人智能控制、無人機飛行控制。

吳亮生，男，1988年生，本科，助理研究員，主要研究方向：圖像處理、數據通訊。

黃煒聰，男，1988年生，碩士，工程師，主要研究方向：管理信息系統開發。

陳惠綱，男，1984年生，本科，工程師，主要研究方向：儀器、儀表開發。

2018年佛山市軍民融合及可持續發展科技項目（2018AG100143）