漆瓊芳，張 苗，蔣士亮

（武漢第二船舶設計研究所，武漢 430064）

目前波動法廣泛用于分析半無限尺寸結構的振動波傳遞特性，對有限尺寸結構，波動法研究對象一般為L型板等兩板耦合結構，而對成任意角度連接的有限尺寸板以及十字型有限板的研究較為不足。船體結構的基座與船底板等連接結構含有十字型結構，研究振動波在耦合處的傳遞特性，可為船舶減振降噪聲學設計提供指導。

Cuschieri J M等采用導納功率流法研究厚、薄L型耦合有限板的功率流，彎曲波數與板厚的乘積小于0.1時，面內振動在低頻時對振動能量貢獻很小[1–2]。Kessissoglou等采用波動法研究有限尺寸L型板的面內波功率流和彎曲波功率流，結果表明，當板成不同角度連接時，會產生面內波與彎曲波的波型轉化[3–4]。趙芝梅等建立L型板的波動法耦合運動模型，研究力和力矩的共同作用對彎曲波和面內波的影響，將劃分的子結構進行模態展開，在連接線處，將點激勵展開成正弦分布的線力[5–6]。薛開等對四邊簡支板矩形厚板進行功率流研究，根據功率流分布圖研究振動能量傳遞特性[7]。劉敬喜等采用波動法研究圓柱殼的功率流，根據面內波功率流和彎曲波功率流所占比例，研究彎曲振動和面內振動[8]。劉春川等采用波動法研究L型板和箱型結構的振動功率流，根據主動功率流和被動功率流進行主動控制[9–12]。

本文將十字型板離散成子結構，離散每個子結構的彎曲波與面內波波幅系數，組裝每個子結構的位移和力向量，采用波動法推導十字型耦合薄板的振動響應公式，得到連接處的平衡方程，并進行MATLAB編程計算十字型板的彎曲波功率流和面內波功率流。對比波動法與有限元法結果，驗證波動MATLAB程序的收斂性與有效性。分析連接角、激勵角等對彎曲波和面內功率流的影響。

1 波動法模型

如圖1，建立波動法力學模型，在點力處與板連接處將十字型板離散成5個離散板，每個離散板ij建立一個坐標系xij、yij、zij，全局坐標系為XYZ，每個離散坐標系均包含力項和位移項。

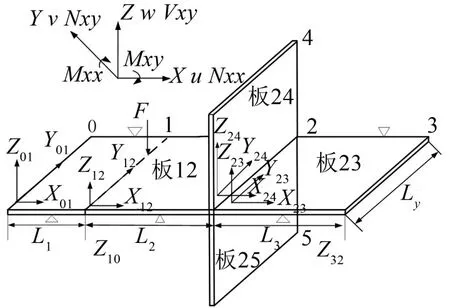
圖1 十字型板的波動法力學模型

對邊簡支矩形板，Poisson-Kirchhoff板的彎曲振動控制微分方程

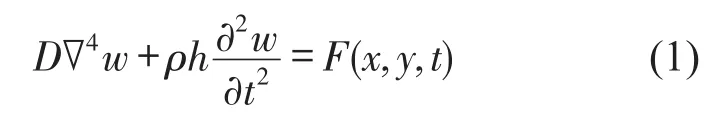
面內振動

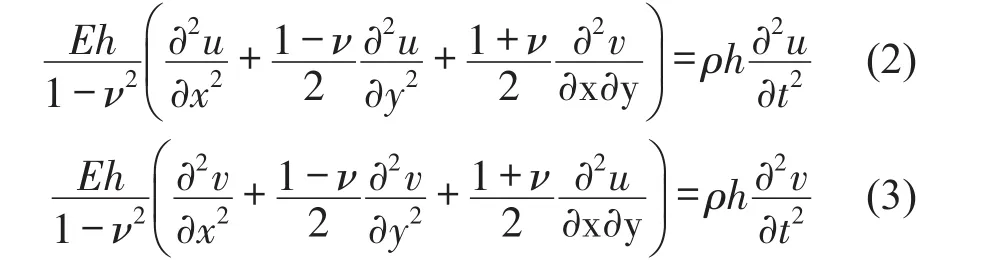
式中w是橫向位移，u是軸向位移，v是y向位移，φx是繞y軸轉角。E是彈性模量，h為板厚，μ是泊松比，F(x,y,t)是外部點力激勵，D=Eh3/[12(1-μ2)]是彎曲剛度，分離薄板的面內振動和面外振動，方程左右兩邊省略eiωt。

離散板01的面內振動

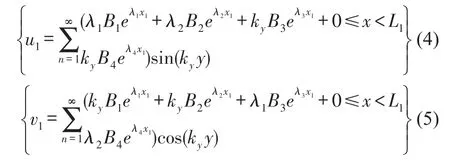
離散板12面內振動

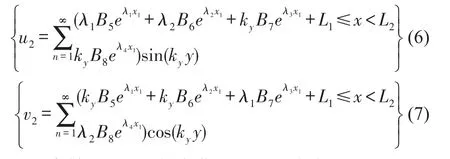
離散板01、12的彎曲運動解依次為

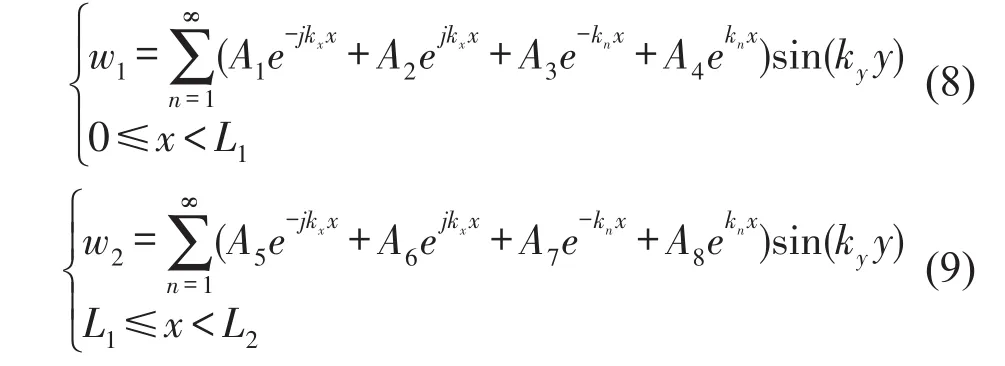
離散板23、34、35的力與位移表達式與離散板12類似，不再贅述。其中，n是模態數，ky=mπ/Ly是y方向波數。kL是縱向波數，kS是剪切波數，kp是彎曲波數，是行進波數。衰減波數。是平面波動解的特征值。Ai(i=1,2,3…4m)是彎曲波波幅系數，Bi(i=1,2,3…4m)是面內波波幅系數，m是離散板數。

力和力矩與位移表達式

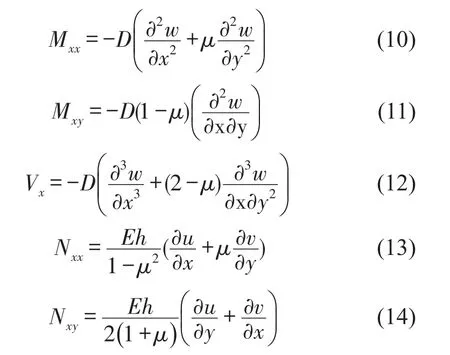
其中Mxx是彎矩，Mxy是扭矩，Nxx面內縱向力，Nxy是剪切力，Vx法向純剪力，耦合力和耦合力矩的方向見圖1。

若板01左端固定

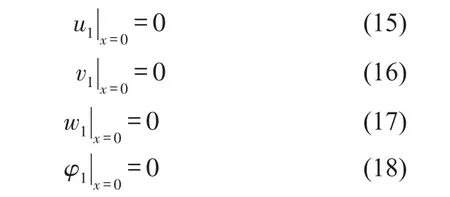
若板01右端有外界點激勵作用

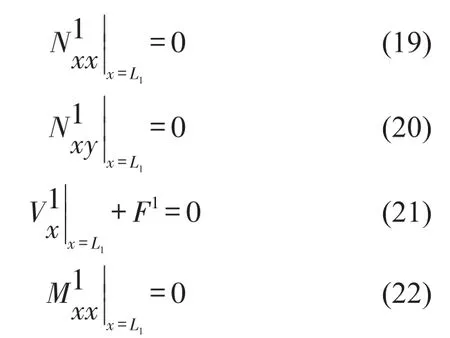
外界點力激勵等效成線激勵級數疊加

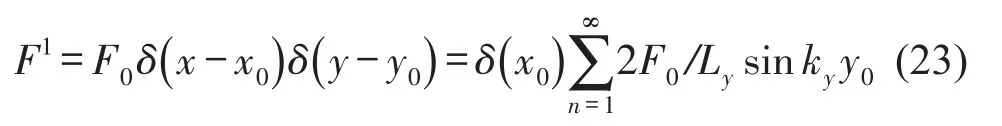
其中F0是激勵力幅值，x0是激勵點橫向局部坐標，

若板01與板12線連續性

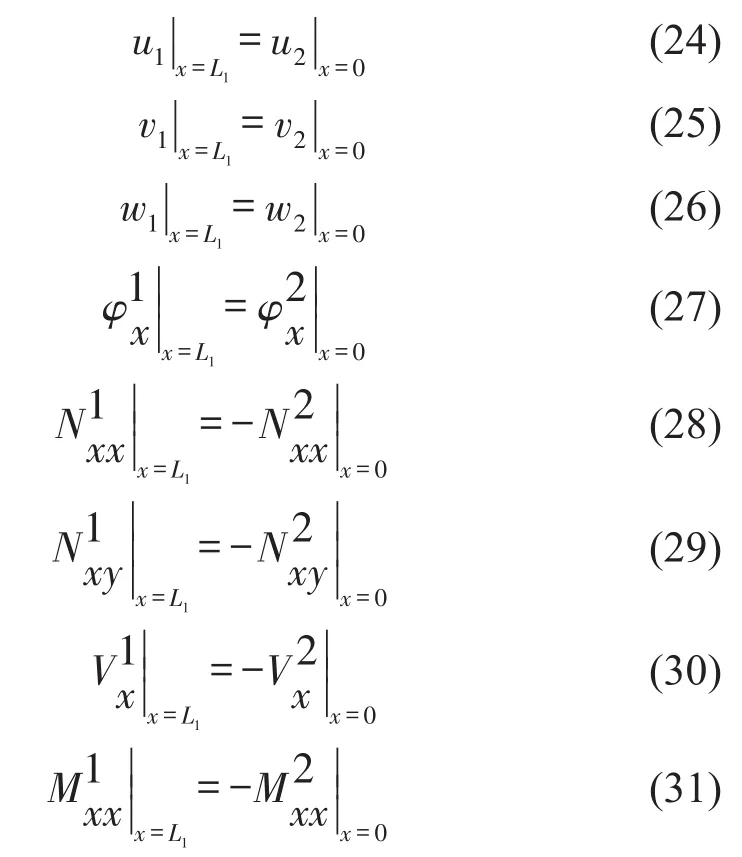
連接線2、3、4、5與連接線0的形式一致，不再贅述。與邊界對于十字型板結構，組裝每個離散板的平衡方程，統一寫成

其中α是十字型板的整體平衡方程組成的矩陣，X是離散板的彎曲波和面內波的波幅系數矩陣的一般形式，F線連接處的外載荷矩陣。振動功率流表示單位時間流過垂直于波傳播方向的單位面積的振動能量，波動法采用功率流來度量振動傳遞能量，波動法的彎曲波功率流和面內波功率流分別為

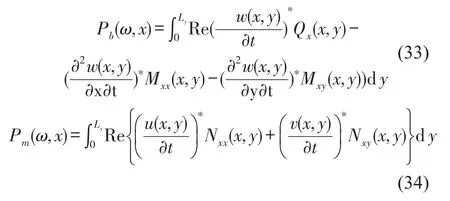
其中?表示共軛復數，Pin是輸入功率流，Pb是彎曲波功率流，Pm是面內波功率流。

2 有效性驗證

2.1 波動法解析解的收斂性驗證

根據波動法推導的十字型板耦合方程，采用MATLAB編程，計算模型響應，輸入參數包括離散板長、板寬及材料屬性等。本模型的泊松比μ=0.3，材料密度ρ=7850kg/m3。彈性模量E=2.06×1011Pa ，復彈性模量Ep=E(1+jη)，損耗因子η=0.01。載荷F=F0eiωt，載荷幅值F0=1 N。對于十字型板結構，取5個離散板，板長均取0.4 m，板寬均為0.6 m，板厚h=12 mm ，連接線0、3、4、5自由，離散板邊界y=0和y=Ly均簡支，激勵點和觀測點在離散板2處的坐標均為（0，0.3）。

采用模態疊加原理，合理選擇模態疊加數可以使結果收斂，其模態收斂性需驗證。根據文獻對于Poisson-Kirchhoff理論的頻率適用范圍的要求，為保證計算精度，計算頻率上限要求，按照經驗公式計算本算例的頻率上限為30 kHz，算例的頻率上限取2 500 Hz，小于經驗公式計算值，滿足薄板理論假設，因此本算例頻率上限取值合理。按經驗公式，不同頻率上限，彎曲波模態疊加數Np、縱波模態疊加數NL、剪切波模態疊加數NS，應滿足表1要求。

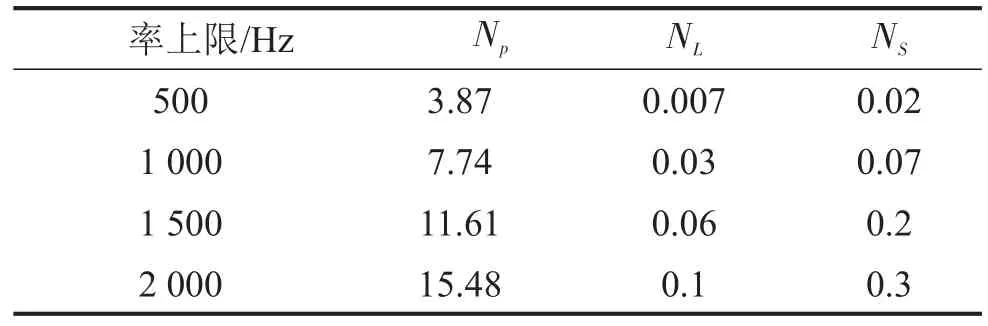
表1 不同頻率下的模態數

當模態疊加數分別取 1、3、5、7時，給出 0～2 500 Hz計算頻域內觀測點處的剪力頻響曲線。由圖2可知，在500 Hz時，模態疊加數N=3時的頻響曲線與N=5時趨近，與N=1時有差別，說明對于波動法，N=3時，頻響曲線已收斂，小于經驗公式計算的3.87。

在1 000 Hz時，模態疊加數N=5與N=7時的頻響曲線吻合較好，N=3時，頻響曲線已經收斂，小于經驗公式計算的7.74。同理，為保證頻響曲線收斂，在1 500 Hz和2 000 Hz時的模態疊加數均小于經驗公式。說明經驗公式給出的最小模態疊加數是偏于保守的，當波動法取經驗公式計算的模態疊加數時，已經收斂。

2.2 波動法解析解的有效性驗證

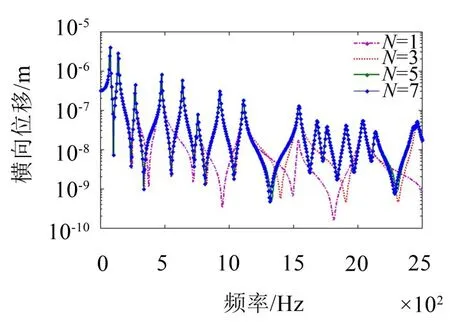
圖2 不同模態疊加數時的頻響曲線

將圖1的十字型板劃分為5個離散板，板長均為0.6m，板寬均為0.4m，板厚h=8 mm，其它參數與2.1節一致。假定板的x邊均簡支，y邊界處均自由。觀測點位于離散板12的（0，0.2）處，激勵點位于離散板01的（0.6，0.2）處，基于波動法的十字型板耦合連接方程，MATLAB編程計算十字型板振動響應的半解析解。

采用Abaqus計算結構響應的有限元數值解，為保證結構動力響應的準確性要求，有限單元長度必須小于彎曲波長的1/6。對于本算例模型，根據文獻經驗公式求出的有限元網格尺寸必須小于0.03，因此模型的有限元網格尺寸為0.02 m×0.02 m可滿足要求。當計算頻率為1 000 Hz，文獻公式要求的截止模態大于7.74，波動法MATLAB程序的模態疊加數目取20滿足要求。波動法半解析法和有限元數值解法的計算頻率上限均取1 600 Hz。如圖3所示，給出觀測點繞y軸轉角的頻響曲線，可知在0～600 Hz計算頻率范圍內，兩種方法的頻響曲線吻合較好，隨著計算頻率的增加，頻響曲線的峰值和相位出現差別，該差異與有限元法的網格密度和波動法的模態疊加數的選擇有關。在頻響曲線低頻范圍內曲線吻合較好，說明耦合連接處的力和位移的平衡方程是準確的，驗證了波動法MATLAB程序的有效性，說明十字型板耦合方程的波動解是有效的。

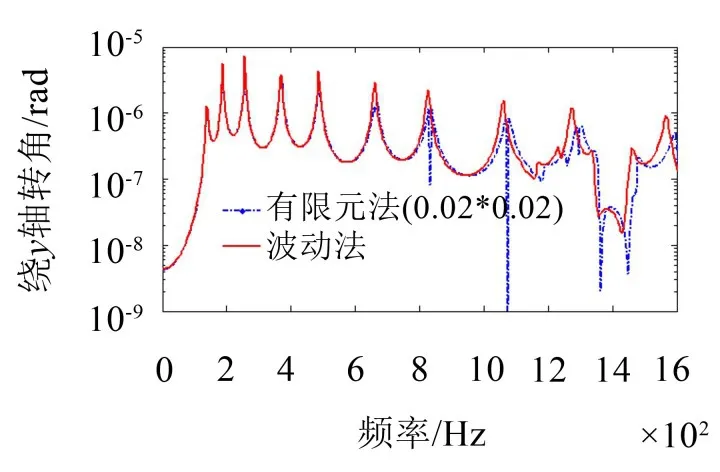
圖3 十字型板的激勵點處繞y軸轉角

3 振動功率流研究

3.1 激勵角振動功率流影響分析

如圖1波動法模型，取3離散板，如L型板，認為離散板01、12為激勵板，離散板23為接受板。板長L1=L2=0.4 m，L3=0.8 m，板寬Ly=0.6 m，板周界均簡支，板材料屬性等參數與2.1節一致。力激勵在離散板01上，坐標為（0.2，0.3）。力激勵與離散板01的局部坐標在x軸方向的夾角定義為激勵角度α，分別取150/450/900，激勵板的觀測截面位于離散板12的x=0處，接受板的觀測截面位于離散板23的x=0.4 m處，采用MATLAB編程計算觀測截面彎曲波功率流和面內波功率流，模態疊加數取20，滿足收斂性要求。

在0～800 Hz范圍內，激勵角變化時，計算激勵板和接受板的彎曲波和面內波功率流。如圖4(a)(b)，激勵板的彎曲波功率流處于10-7數量級，面內波功率流處于10-12數量級，彎曲波功率流比面內波功率流大得多，可以忽略面內波功率流。圖4(b)與圖4(d)對比，除功率流峰值附近頻率范圍，激勵板的面內波功率流均隨激勵角度的減小而增大，接收板的面內波功率流均隨激勵角度的減小而減小。

圖4(a)與圖4(c)對比，兩板的彎曲波功率流均隨激勵角度的減小而減小。對比圖4(c)與圖4(d)，接受板的彎曲振動和面內振動均隨激勵角的減小而減小。

在8 kHz～9 kHz高頻范圍內，圖5顯示了波動法MATLAB程序計算的兩板的彎曲波功率流和面內波功率流。對比圖5(a)與圖5(b)，彎曲波功率流在10-6數量級，面內波功率流在10-7數量級，面內振動相對于彎曲振動不可忽略。對比5(a)與圖5(c)，激勵板和接受板的彎曲波功率流均隨激勵角的增加而增大。對比圖5(b)與圖5(d)，兩板的面內波功率流與激勵角沒有呈現明顯規律。

對比可知，在低頻范圍內，激勵板面內波功率流峰值隨激勵角度的減小而增大，接受板面內波功率流峰值隨激勵角度的減小而減小。在全頻范圍內，兩板的彎曲振動均隨激勵角度的減小而減小。彎曲波與面內波在不同頻率階段呈現如下變化趨勢：

（1）在頻率較低階段，彎曲波明顯大于面內波，可以忽略面內振動；

（2）在頻率較高階段，彎曲波和面內波數量級相當，不可忽略面內振動；

（3）在低頻和高頻階段，激勵板的彎曲振動均隨激勵角的減小而減小。

該現象是激勵板能量主要源于力激勵的導致直接振動和L型板在連接線處的波形轉化引起的。

（1）從激勵方面分析：隨激勵角的減小，力在板內的分量增大，垂直于板的分量減小，激勵板由力激勵引起的彎曲振動增大而面內振動減少。

（2）從波形轉換方面分析：隨激勵角的減小，激勵板彎曲振動減小，彎曲波在L型接頭處轉化為面內波減弱，因此接受板的面內波隨激勵角度的減小而減小。

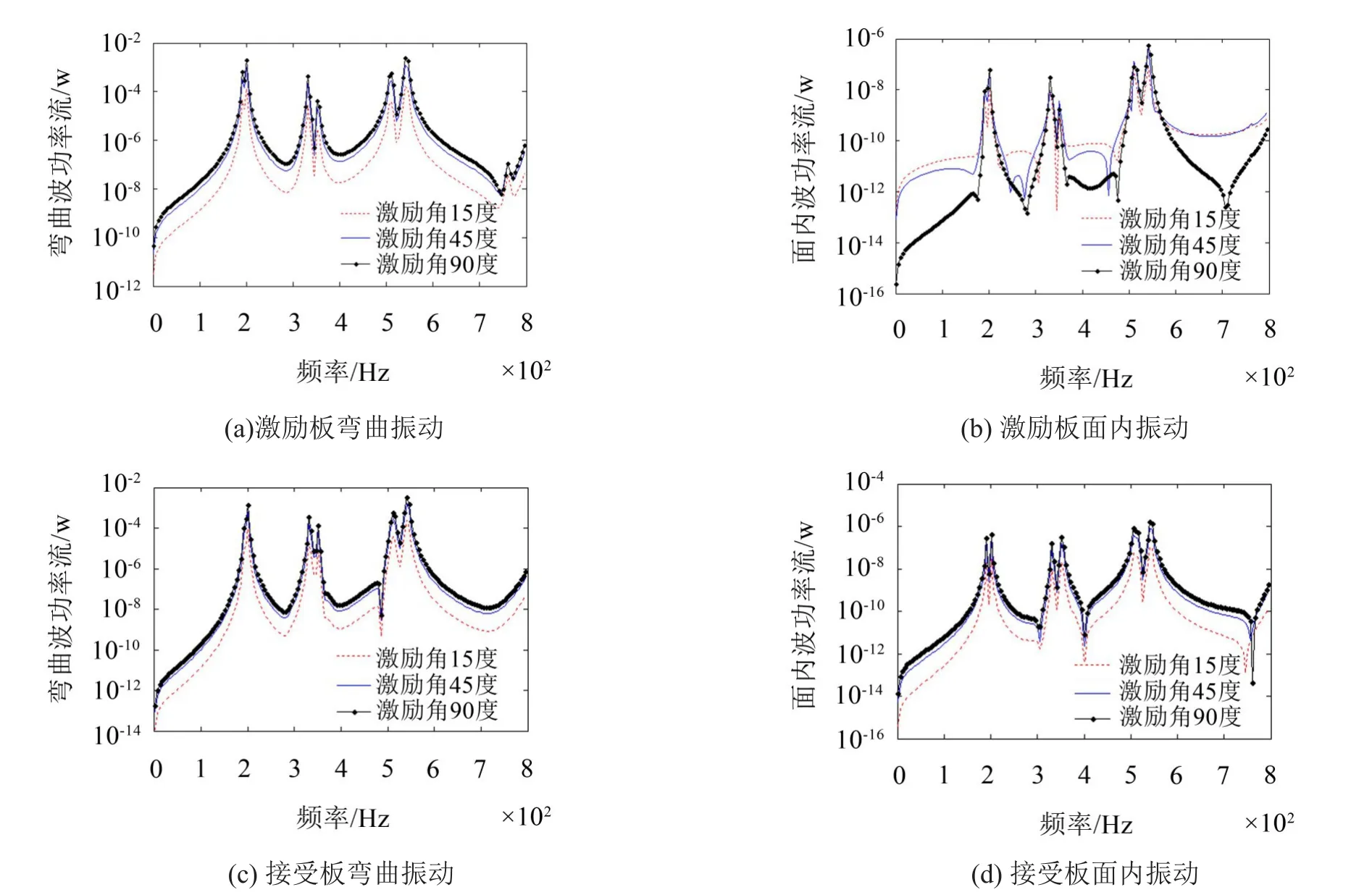
圖4 不同激勵角時的低頻段功率流

（3）在頻率較高階段，彎曲波和面內波與激勵角沒有明顯規律，是力激勵和波形轉換綜合相反作用導致。

（4）在頻率較低階段，板縱向剛度遠大于彎曲剛度，板的彎曲振動較大，隨頻率的增加，彎曲剛度和縱向剛度數量級接近，所以力激勵水平分量直接引起的面內振動隨頻率的減小而減小。

3.2 不同板連接角時的波型轉換關系

對于L型板，尺寸與3.1一致。在力激勵作用下，在不同板連接角時，分別計算接受板的彎曲波功率流和面內波功率流。計算頻率范圍取0～500 Hz，如圖6所示。

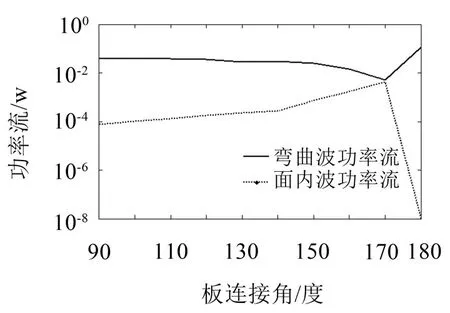
圖6 低頻時彎曲波和面內波功率流

當板12與23的連接角處于90°～180°，彎曲波功率流在10-2數量級，面內波功率流在10-4數量級，面內波功率流比彎曲波功率流少，面內波可以忽略。連接角在90°～170°之間時，面內波功率流隨著連接角的增大而增大，而彎曲波功率流有緩慢減小的趨勢；板連接角為180°時為平板結構，面內波功率流最小，彎曲波功率流最大，平板結構不存在激勵板的彎曲波在L型接頭處轉為為接受板的面內波，因此接受板的面內振動很小，振動能量主要來自彎曲振動。總功率流是彎曲波功率流與面內波功率流之和，當面內波功率數量級遠小于彎曲波時，總功率流的數量級與彎曲波一致。

當計算頻率范圍取7 500 Hz～8 000 Hz，如圖7所示，板連接角在90°～120°范圍內，接收板的面內波功率流和彎曲波功率流均隨連接角的減小而緩慢增大，接受板的面內波功率流比彎曲功率流大，因連接角90°～120°時，激勵板的彎曲振動轉化成接受板的面內振動，在板連接處阻抗失配，振動能量損耗較大。板連接角為90°時，接收板的面內波功率流最大，處于10-3的數量級，此時接受板的面內振動主要來自激勵板的彎曲振動的轉化；板連接角在120°～170°范圍內，彎曲波功率流逐漸增大，結構趨近于平板結構，振動能量主要是彎曲振動。

圖6與圖7對比可知，高頻階段的面內波功率流大于低頻階段。

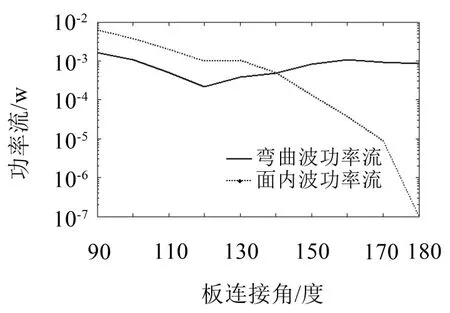
圖7 高頻時彎曲波和面內波功率流

低頻階段，面內波功率流相對于彎曲波功率流可以忽略不計。板連接角90°時，接受板的面內波最大，振動能量主要來自于激勵板的彎曲波在L型接頭處的轉化。板為180°時，面內振動最小，導致彎曲振動的能量直接來自于激勵力。

4 結語

對于有限尺寸板，通過彎曲波和面內波波幅系數矩陣的組合與離散，可以得到有限板在連接處的耦合運動方程的一般形式，該一般形式為耦合方程的解耦和MATLAB編程提供便捷，將波動法的應用擴展到考慮邊界條件的十字型等多板耦合結構，功率流分析表明：

（1）板受到多點力激勵，將點力激勵通過傅里葉級數展開轉化為線性激勵，將多個線激勵進行線性疊加，將疊加后的結果作為結構的外界激勵，MATLAB編程計算板受多點激勵力時的結構響應，線性激勵力疊加的有效性通過有限元數值解得到驗證。說明經驗公式給出得最小模態疊加數是偏于保守的，當波動法取經驗值時，已經收斂。

（2）頻率較低階段，彎曲波功率流明顯大于面內波功率流，面內波功率流可以忽略；在全頻域范圍內，激勵板的彎曲振動功率流均隨激勵角度的增大而增大，而接受板面內波功率流是激勵板波形轉化和直接力激勵綜合作用的結果，隨激勵角無明顯規律。

（3）頻率較高時的面內波功率流大于頻率較低階段。在頻率較低階段，面內波功率流相對于彎曲波功率流可以忽略。板連接角90°時，接受板的面內波最大，面內振動能量主要來自激勵板彎曲波在L型接頭處的轉化。板連接角180°時，面內振動最小，振動能量主要來自激勵力。在結構聲學設計時，板連接角盡量處于90°左右，此時接受板的振動功率流較小，彈性波在此結構型式下衰減較大。

[1]CUSCHIER J M.Parametric analysis of the power flow on an L-shaped plate using a mobility power flow approach[J].Journalofthe AcousticalSocietyof America,1992,91(5):2686-2695.

[2]CUSCHIER J M,MCCOLLUM M D.In plane and out-ofplane wave’s power transmission through an L-plate junction using the mobility power flow approach[J].Journal of the Acoustical Society of America,1996,100(2):857-70.

[3]KESSISSOGLOU N J,JIE PAN.An analytical investigation of the active attenuation of the plate flexural wave transmission through a reinforcing beam[J].Journal of the Acoustical Society of America,1997,102(6):3530-3541.

[4]KESSISSOGLOU N J.Power transmission in L-shaped plates including flexuraland in-plane vibration[J].Journal of the Acoustical Society of America,2004,115(3):1157-1169.

[5]趙芝梅，盛美萍.激勵特性對L型板振動功率流的影響[J].兵工學報，2013，34(8)：986-993.

[6]趙芝梅，盛美萍，楊陽.多點激勵下加筋板殼耦合結構的振動特性[J].工程力學，2013，31(11)：239-244.

[7]薛開，王久法，李秋紅，等.中厚矩形板的振動功率流特性分析[J].振動與沖擊，2013，32(21)：78-181.

[8]劉敬喜，譚安全，李天勻，等.復合材料層合圓柱殼中振動功率流特性[J].哈爾濱工程大學學報，2012，33(2)：269-274

[9]LIU C C,LI F M,FANG B,et al.Active control of power flow transmission in finite connected plate[J].Journal of Sound&Vibration,2010,329(20):4124-4135.

[10]LIU C C,LI F M,FANG B,et al.The wave and vibratory power transmission in a finite L-shaped mindlin plate with two simply supported opposite edges[J].Acta Mechanica Sinica,2011,27(5):785-795.

[11]LIU C C,LI F M,HUANG W H.Transient wave propagation and early short time transient responses of laminated composite cylindrical shells[J].Composite Structures,2011,93(10):2587-2597.

[12]LI F,LIU C C.Analysis and experiment on transient dynamic response in finite mindlin plate[J].Acta Mechanica Solida Sinica,2013,26(2):129-139.