基于譜峭度與變分模態分解的轉子微弱不對中故障診斷

唐貴基，王 菲，周福成，趙 晨

（華北電力大學 能源動力與機械工程學院，河北 保定 071003）

由于機器的安裝誤差、工作狀態下熱膨脹、承載后的變形以及機器基礎的不均勻沉降等，有可能會造成機器工作時各轉子軸線之間產生不對中[1]。不對中是轉子系統一種典型的故障，具有不對中故障的轉子系統在其運轉過程中將產生一系列有害于設備運行的動態效應，如引起設備的振動、機器聯軸器偏轉、軸承早期損壞、油膜失穩和軸的彎曲變形等，導致機器發生異常振動危害極大，其振動信號具有非線性特征，例如，具有倍周期、倍頻、工頻振動及混沌現象等特征[2]。然而，由于在強烈的背景噪聲下，信號中不對中故障特征不明顯，即存在微弱不對中故障，則對于故障特征的提取存在一定程度困難。常見的非線性、非平穩處理方法有：小波變換、經驗模式分解（EMD）、總體經驗模式分解（EEMD）等。小波變換可以有效抑制白噪聲，但是抑制脈沖干擾能力不強；EMD是分析非平穩信號和非線性信號強有力的工具，但是存在缺乏嚴格的數學基礎、算法效率低、模式混疊問題。EEMD是在EMD基礎上的改進算法，能有效抑制模態混疊現象，但是算法效率低[3]。

針對EMD方法存在的不足，Dragomiretskiy等于2014年創造性地提出了一種新的完全非遞歸自適應信號處理方法，即變分模態分解（VMD）方法。該方法的核心思想是假設每個模態的絕大部分都是緊緊圍繞在某一中心頻率周圍的，然后將模態帶寬的求解問題轉化為約束優化問題，求解出每個模態[4]。變分模態分解具有堅實的理論基礎，相比經驗模態分解和局部均值分解的遞歸“篩選”模式，VMD將信號分解轉化非遞歸、變分模態分解方式，在很多方面表現出更加優異的性能[5]。然而，直接對含有噪聲的信號進行VMD分解得到的IMF里同樣含有噪聲，影響IMF的準確度。為有效提取機械故障特征，首先必須濾除信號背景噪聲以強化故障特征相關信號分量。通過保留主要低頻諧波和調制分量并濾除其余背景成分，可顯著提高原信號信噪比。該策略的關鍵在于依據信號特點自適應構建帶通濾波器組。近年來，譜峭度已被成功應用于背景干擾下信號沖擊性特征的檢測，其對非平穩信號分量的敏感性可為自適應帶通濾波器組的設計提供參考[6]。

1 變分模態分解

VMD是一種新的信號分解估計方法，其將原始信號放入多個變分約束框架內，通過迭代搜尋變分模型最優解，從而確定每個分解分量的頻率中心和帶寬，可以自適應地將信號分解成具有稀疏特性的分量。在此僅對變分問題的構造和求解進行介紹，詳細步驟可參考文獻[7]。

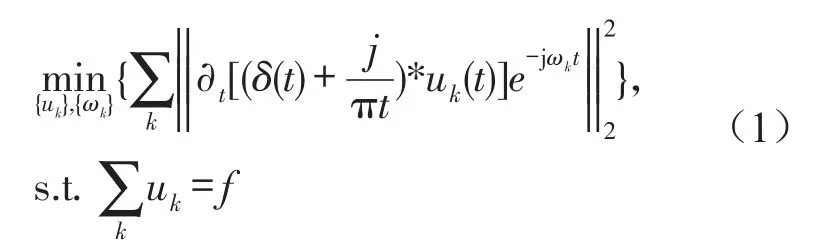
式中δ(t)為Dirac分布；*表示卷積；k=1,2，…，K；f為原始信號。

為求取變分約束模型的最優解，引入二次懲罰因子α和Lagrange乘子λ，其中α為足夠大的正數，可在高斯噪聲存在的情況下保證信號的重構進度，拉格朗日算子使得約束條件保持嚴格性，可得

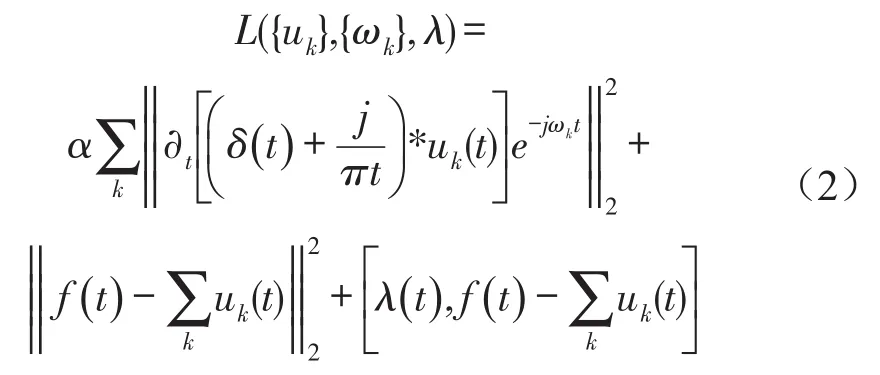
VMD采用乘法算子交替的方法求取上述變分約束模型，得到最優解將信號分解成為K個窄帶IMF，實現流程圖如圖1所示。

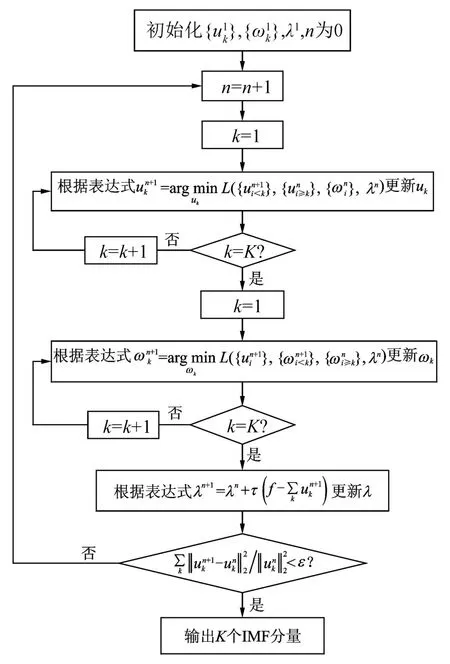
圖1 VMD算法流程圖

VMD算法處理信號時需要預先設定模態分量個數K，不同的分解個數會對分解結果產生影響，從而影響最終的診斷，因此選擇合適的模態分解個數是將VMD應用于故障診斷的關鍵。

2 譜峭度

Dwyer首先提出了譜峭度（Spectral Kurtosis，SK）法[8]，用于克服功率譜無法檢測和提取信號中瞬態現象的問題，其基本思路是計算每個譜線的峭度值，從而發現隱藏的非平穩的存在，并指出它們出現在哪些頻帶[9]。Antoni對譜峭度進行了深入的研究，在文獻[10–11]中詳細闡述了基于譜峭度的理論基礎，正式給出了譜峭度的數學定義，并將其成功應用到旋轉機械的故障診斷中[12]。在非平穩情況下，定義Y(t)為由信號x(t)激勵的系統響應，其Woldcramer分解的頻域表達式為

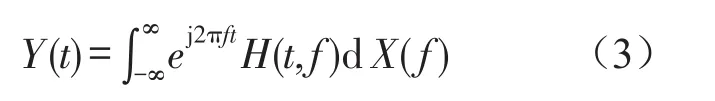
式中H(t,f)是系統的時變傳遞函數，表示Y(t)在頻率f處的復包絡。

定義Y(t)的4階譜累計量為

雜散電流腐蝕防護主要由參比電極、接線盒、引出端子、電纜、排流柜、雜散電流監測裝置等設備組成。這些設備的性能、功能設置的優劣將直接影響雜散電流腐蝕防護工程功能及作用的發揮。

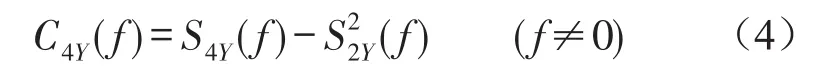
式中S2nY(f)是譜瞬時距，用來度量復包絡能量，定義為

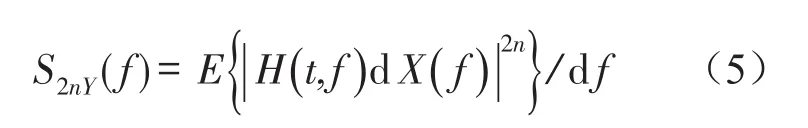
將譜峭度定義為歸一化累計量表示為

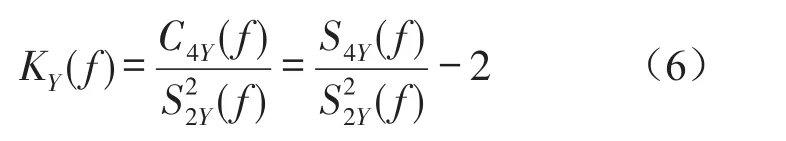
文獻[10–11]中為了獲取基于譜峭度的最優濾波器的參數，將譜峭度作為STFT窗口寬度的函數提出了峭度圖的概念。由于計算中心頻率和STFT窗口所有組合的峭度圖費時又不便于工程實踐的應用，文獻[13]進一步提出了快速峭度圖的概念。在原理上類似于離散小波包分解的快速算法，能夠得到與峭度圖同一水平的結果但是計算時間顯著減少。在二維快速峭度圖像中橫坐標代表頻率f，縱坐標則表示分解的層數K，頻率分辨率Δf=2-(K+1)fs，圖像上的顏色深淺表示不同f和Δf下的SK值。

3 基于譜峭度與VMD的轉子微弱不對中故障診斷

本文使用譜峭度與VMD相結合的方法對具有微弱不對中故障的轉子進行診斷。首先借助于譜峭度方法對原始振動信號去噪以提高信噪比，然后利用VMD對去噪后的信號進行分解，并對各分量做頻譜，提取出故障特征并進行分析。具體步驟如下：

（1）計算原始信號的快速峭度圖，將其最大峭度處的載波頻率和帶寬當作濾波器的最優濾波參數對信號進行降噪處理；

（2）以初始化模態數K=2，懲罰因子α=2 000，帶寬τ=0對去噪后的信號進行變分模態分解，并觀察每個模態分量的中心頻率，如果相近，則確定模態數K=K-1,否則以模態數K=K+1進行步驟（2）；

（3）對步驟（2）分解出的各分量作頻譜圖；

（4）分析步驟（3）中的各頻譜圖，提取故障特征。

4 轉子不對中故障分析

利用Bently RK-4轉子實驗臺進行了轉速為3 045 r/min即頻率50.75 Hz的不對中故障實驗，信號采樣頻率為1 280 Hz。在單盤轉子兩側安裝電渦流傳感器測量軸徑向位移振動信號，在一側軸承座四角加墊片，模擬平行不對中。

將采集所得振動信號輸入MATLAB進行分析，時域波形如圖2所示，對應的頻譜圖如圖3所示。

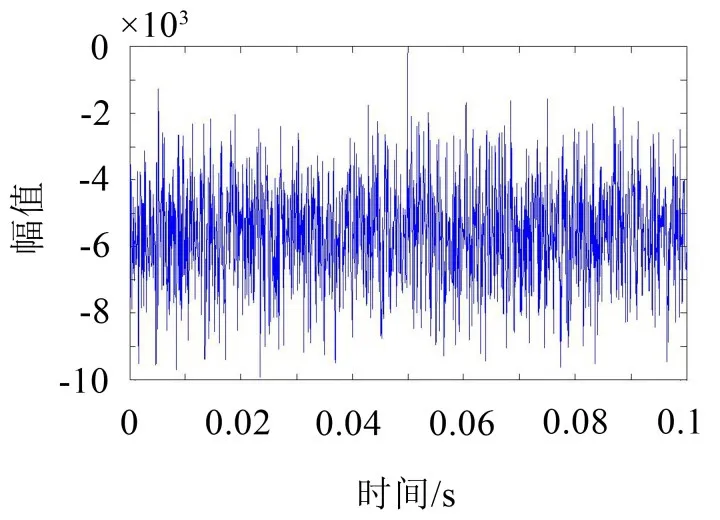
圖2 原始信號時域波形圖

觀察兩圖可以發現，由于噪聲強度太大從圖2中并不能發現故障特征頻率，圖3中只能看到一倍頻成分，不能提取出其他倍頻即故障特征頻率成分。所以首先借助于譜峭度方法對原始振動信號去噪以提高信噪比。

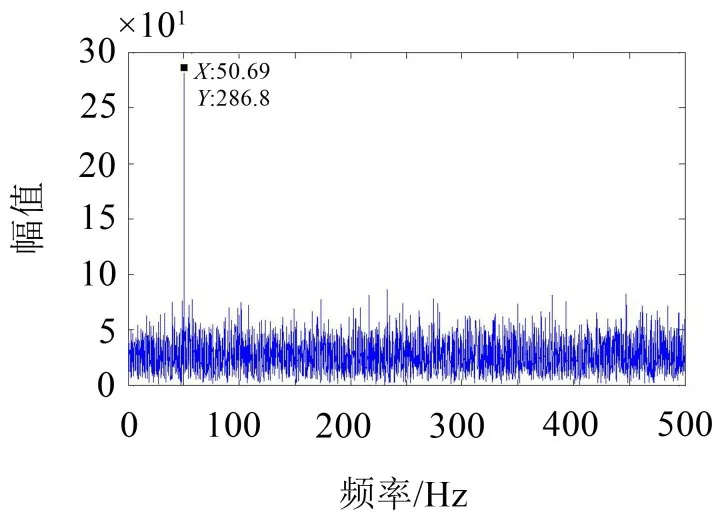
圖3 原始信號頻譜圖

計算該信號的快速峭度圖，將其最大峭度處的載波頻率和帶寬當作濾波器的最優濾波參數對信號進行降噪處理，快速峭度圖如圖4所示。

以第8層、載波頻率0.308 59 Hz進行濾波，保存濾波后信號。

對濾波后的信號進行VMD分解，由上述步驟（2）中的方法確定模態數K=6，懲罰因子α=2 000，帶寬τ=0。分解結果如圖5所示。

然后對圖5中的各分量作頻譜，由于篇幅限制沒有將各頻譜圖一一展示，根據轉子基頻與倍頻特征挑選出具有故障特征的分量進行分析，頻譜圖如圖6所示。

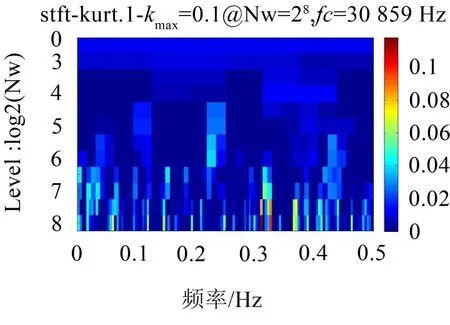
圖4 快速峭度圖

由圖6中IMF1分量頻譜圖可以發現明顯的1倍頻成分，IMF2分量頻譜圖雖然仍然存在噪聲成分的干擾，但是2倍頻成分也被提取出來。所以可以推斷轉子發生了不對中故障。

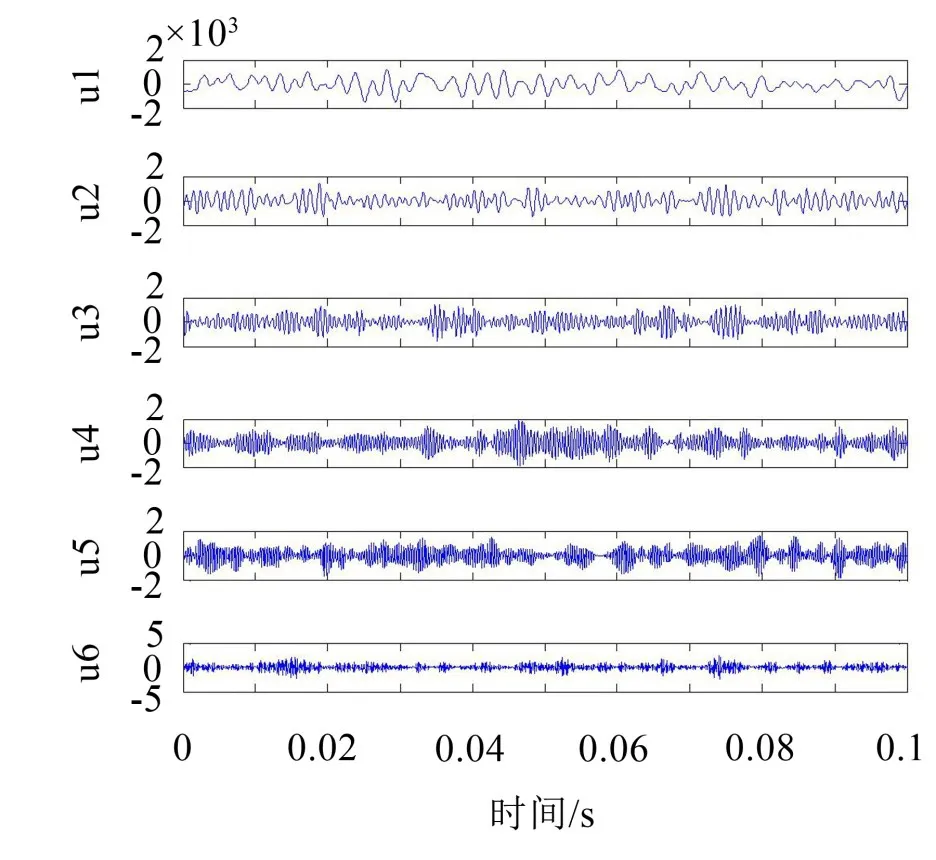
圖5 VMD分解結果

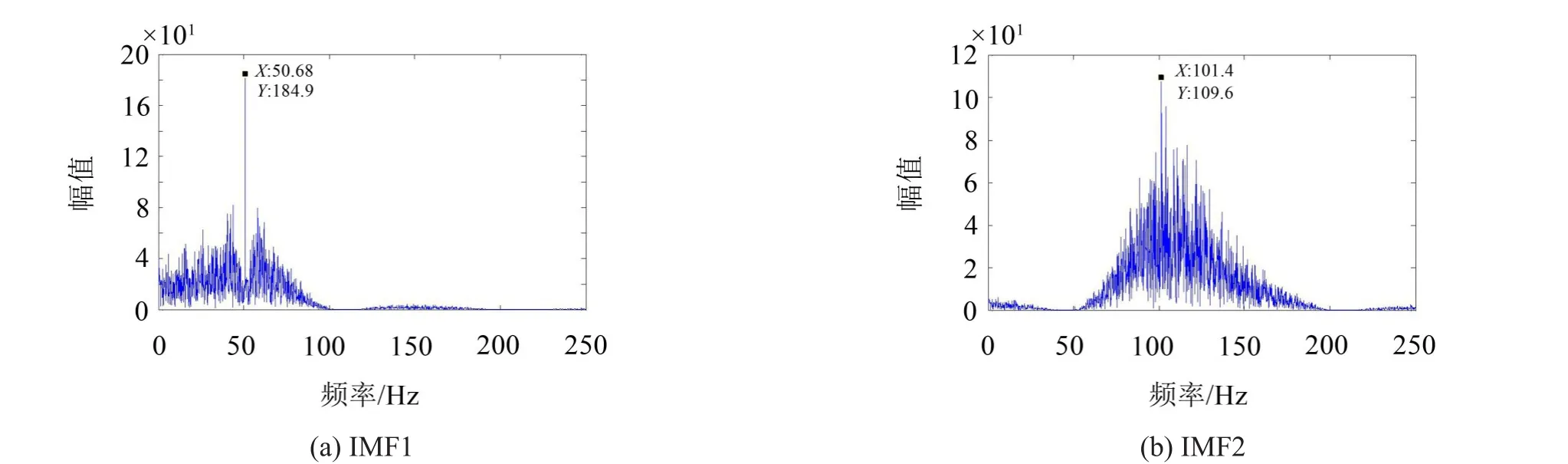
圖6 VMD分量頻譜圖

為了證明譜峭度與VMD分解相結合方法的優越性，本文用基于譜峭度與EMD分解的方法對同一轉子微弱不對中故障信號進行故障特征提取并且做對比分析。對以上譜峭度去噪后保存的信號進行EMD分解，分解結果如圖7所示。

同樣的，對圖7中的各分量作頻譜，并挑選出具有故障特征的分量進行分析，頻譜圖如圖8所示。

由圖8中IMF4分量頻譜圖同樣可以發現明顯的1倍頻成分，但是通過IMF3分量頻譜圖發現，分量受噪聲干擾嚴重，頻譜圖中96.45 Hz和103.8 Hz都不是2倍頻成分。所以，譜峭度與EMD分解相結合的方法不能診斷出轉子微弱不對中故障。

通過譜峭度分別與VMD分解和EMD分解相結合的方法對比分析可得，VMD分解精度高，分解層數少，具有更好的噪聲魯棒性，并且有效避免EMD分解過程中的模態混疊現象，在信號處理分析領域具有廣闊的應用前景。

5 結語

針對轉子微弱不對中故障容易淹沒在噪聲中，導致其故障特征信息難以提取的問題，本文提出一種基于譜峭度與VMD分解的轉子微弱不對中故障診斷方法。實驗分析結果表明，該方法能夠準確地識別轉子微弱不對中故障。與譜峭度和EMD分解相結合的方法相比，本文方法的診斷更加精確，易取得更優的診斷效果。

圖7 EMD分解結果

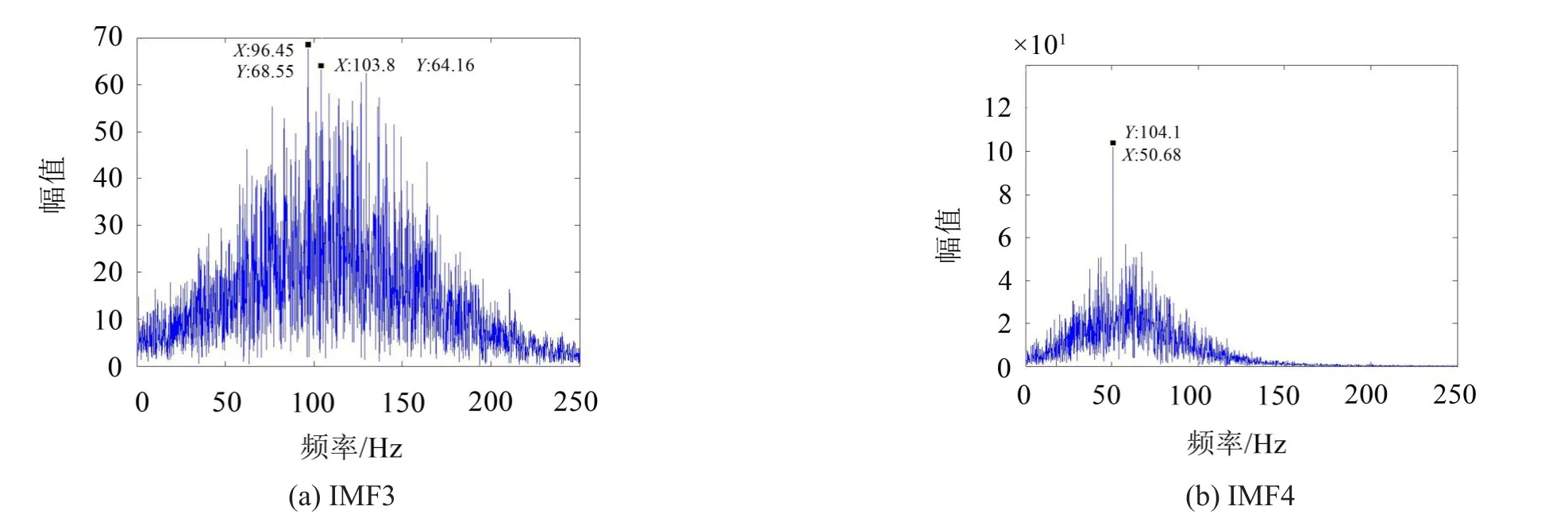
圖8 EMD分量頻譜圖

[1]張祖德，王玉強.旋轉機械轉子不對中的故障診斷[J].特鋼技術，2010，16(65)：56-59.

[2]郭興，李明.諧波小波法在轉子不對中故障診斷中的應用[C].第九屆全國動力學與控制會議，2012.5：207-208.

[3]錢林，康敏，傅秀清，等.基于VMD的自適應形態學在軸承故障診斷中的應用[J].振動與沖擊，2017，36(3)：227-233.

[4]李志農，朱明.基于變分模態分解的機械故障診斷方法研究[J].兵工學報，2017，38(3)：593-599.

[5]石敏，李影，王冰，等.基于變分模態分解的齒輪箱故障診斷[J].電力科學與工程，2016，32(1)：23-26.

[6]張兵，于淑靜，董紹江.基于譜峭度和多元經驗模式分解的機械故障診斷[J].設計與研究，2015(6)：97-101.

[7]DRAGOMIRETSKIY K,ZOSSO D.Variational mode decomposition[J].Signal Processing,IEEE Transactions on,2014,62(3):531-544.

[8]DWYER R F.Detection of non-Gaussian signal by frequency domain kurtosis estimation[C].Acoustic,Speech and Signal Processing.Boston:IEEE International Conference on ICASSP,1983:607-610.

[9]蘇文勝，王奉濤，張志新，等.EMD降噪和譜峭度法在滾動軸承早期故障診斷中的應用[J].振動與沖擊，2010，29(3)：18-21.

[10]ANTONI J,RANDALL R B.The spectral kurtosis:a useful tool for characterizing non-stationary signals[J].Mechanical Systems and Signal Processing,2006,20(2):282-307.

[11]ANTONI J,RANDALL R B.The spectral kurtosis:application to the vibratory surveillance and diagnostics of rotating machines[J].Mechanical Systems and Signal Processing,2006,20(2):308-331.

[12]彭暢，柏林，謝小亮.基于EEMD、度量因子和快速峭度圖的滾動軸承故障診斷方法[J].振動與沖擊，2012，31(20)：143-146.

[13]ANTONI J.Fast computation of the kurtogram for the detection of transient faults[J].Mechanical Systems and Signal Processing,2007,21(1):108-124.

[14]隆軍，吳金強.風力發電機組轉子不對中故障診斷[J].噪聲與振動控制，2013，33(3)：222-225.

[15]王磊，紀國宜.基于EMD模糊熵和SVM的轉子系統故障診斷[J].噪聲與振動控制，2012，32(3)：171-176.