非參數計量經濟學中的偽回歸診斷

(天津財經大學理工學院,天津300222)

1 引 言

當數據存在趨勢時,回歸分析可能將無關變量擬合出顯著的關聯關系.這樣的分析會得出錯誤的結論、做出無效的預測,即發生所謂的虛假回歸,給實證研究和預測工作帶來風險[1].這就要求學者對模型是否存在偽回歸的問題進行診斷,以識別和降低這種風險.在研究當中,參數模型的偽回歸診斷已經得到了廣泛的重視[2],而非參數模型的偽回歸診斷卻常常會被人忽視.主要原因在于,非參數模型沒有在形式上做主觀預設,它們常常被當作最接近真實、決不會犯錯的模型.但事實并非如此.在趨勢的影響下,參數模型尚且容易錯把無關變量擬合出關聯關系,作為擬合能力更強的非參數模型,就可能面臨更大的偽回歸風險.但考慮到非參數模型并沒有描述關聯關系的表達式,即便模型存在風險,又該診斷什么,如何診斷呢？本文研究了非參數模型的偽回歸診斷問題,試圖為相關檢驗方法給出嚴格的理論論證和較全面的應用參考.

關于偽回歸診斷的問題,有些重要的文獻做出了有價值的研究.Granger等[3]基于模擬實驗,率先研究了單位根過程帶給參數模型的偽回歸問題,并提出基于DW統計量的回歸診斷方法.方法的基本思想是用殘差的全局特征來診斷參數模型的表達式是否可靠.在此基礎上,Phillips[4,5]研究了單位根過程回歸殘差的漸進分布特征,推導和完善了方法的理論基礎.但該方法并不適合診斷非參數模型.非參數回歸是一種關注局部的逐點估計,殘差關聯機制與參數模型不同,局部之間缺乏相關性.Phillips[6]分析了這個問題,并創造性地提出了局部診斷的思想,研究了數據隨機趨勢帶給局部殘差特征的影響.Kasparis等[7]沿用了局部視角的檢驗設計思想,研究了在多元動態時間序列的分析當中,選錯解釋變量滯后期時非參數回歸的殘差異常性質.這些診斷方法的共同思路是,設計統計量考察數據趨勢屬性帶給非參數回歸殘差的影響,用非參數回歸殘差的局部特征來診斷原始數據的趨勢屬性.偽回歸診斷的初衷是辨別有風險的回歸,但現有的研究并沒有把非參數模型中“殘差局部特征”和“估計失真風險”的關聯關系說清楚,可見局部DW診斷方法的理論基礎有待進一步論證.診斷在不同窗寬、不同樣本容量的回歸當中可能遇到的問題,也有待進一步研究.

本文回顧了隨機趨勢給非參數模型帶來的偽回歸風險,并針對現有文獻的不足,在Phillips局部診斷思想的基礎上,研究了非參數回歸中殘差局部性質和模型估計風險的關聯關系.用數學語言描述回歸風險,并通過數學變換,創造性地將回歸的診斷問題轉化成了級數收斂的檢驗問題,解釋了數據局部特征與局部回歸風險之間的聯系.還通過模擬實驗,考察了不同類型非參估計的偽回歸診斷,給出了診斷的一般步驟且驗證了診斷的功效.發現,局部殘差性質異常是非參數模型估計失真的充分條件,而局部DW檢驗可以很好地識別這種情況,進而診斷非參數模型的偽回歸.文章完善了使用局部特征診斷回歸風險的理論基礎,具有較強的理論意義；歸納了檢驗方法在模擬實驗中表現出的若干性質,為非參數模型的實際應用提供參考.

2 問題的初探

誤設模型的擬合優度通常很低,因此研究常用擬合優度指標來評價模型的可靠性.但當數據存在趨勢時,擬合優度指標可能會出現虛高,容易讓人把誤設的模型當作正確的模型.這就是虛假回歸或偽回歸.這種“虛假”是由趨勢造成的.

在實際經濟當中,時間序列的數據生成過程普遍受到多方面因素的影響.其中可能存在一部分影響幾乎不隨時間推移而有所衰減,這部分影響不斷累積,形成了數據的趨勢.時間序列的趨勢可以分成如下幾類,即線性趨勢、非線性趨勢、變結構現象和隨機性趨勢[8].趨勢有時會給數據分析帶來干擾,進而導致模型的誤設.

趨勢是識別和描述數據生成過程的重要工具.可以運用發現趨勢、擬合趨勢(通常用虛擬變量、傅立葉展開或非參數形式擬合)和去勢等技術,逐步將包含確定性趨勢的數據轉換成無趨勢數據[9].確定性趨勢在很大程度上是可預測、可處理的.但如果序列存在隨機趨勢,情況則變得復雜.隨機性趨勢表現為數據的長記憶性(常見的有單位根過程和分數單整過程),這種性質打斷了時間序列不同位置間數據屬性的遞推機制,給數據分析工作帶來了嚴重的誤導.對于確定存在關聯關系的變量,可用誤差修正模型建模,探索變量間的影響機制[10].在不確定關聯關系時,使用回歸方法研究變量關系就可能將無關變量擬合出某種關聯關系,研究就是要識別這種回歸.

為了直觀地展示非參數回歸中偽回歸的問題,下面用模擬實驗舉例,使用非參數模型對單位根過程做回歸分析.設三個隨機序列ut,vt,ξt服從標準正態分布,用它們定義三個非平穩過程xt,yt,zt.首先生成單位根過程x序列；然后借助x序列生成y序列,此處不失一般性地設定二者存在正相關的線性函數關系；最后生成了一個與前兩個序列無關的單位根過程z序列.

數據生成過程的數學表達式如下

其中k取正整數,用來控制y序列的波動幅度,令k=1,序列設為100期.

對生成的數據多次重復下面的回歸,即式(4)～式(6).

當變量間相關系數較高時,回歸容易產生較高的擬合優度.在考察回歸擬合優度之前,不妨先查看自變量和因變量間的皮爾遜相關系數,實驗重復1 000次,結果見圖1.

圖1 相關系數直方圖Fig.1 Histogram of the correlation-coefficients

根據式(1)～式(3)可以看出,y序列與x序列存在函數關系,而y與z和v與u均不存在關聯關系.由圖1可以看出,當數據不存在隨機趨勢,無關序列不會呈現出顯著的相關特征,v與u的相關系數集中在(-0.2,0.2)；當數據存在隨機趨勢時,無關序列相關系數盡管期望為0,但有時表現出顯著的正相關,有時表現出顯著的負相關,實驗產生的相關系數幾乎是均勻分布在(-1,1)的區間里；如果數據本身存在關聯關系,y與x表現出顯著的相關關系,與實驗的設定相符,相關系數集中在(0.97,1.00)的區間里.

比較三個回歸的擬合優度.回歸1中的變量不存在趨勢,擬合優度集中在0附近.用非參數回歸分析非平穩數據(即回歸2和回歸3)是下面研究的重點.采用不同窗寬實施模擬實驗研究這兩組回歸的擬合優度,研究結果見圖2,圖(a),圖(b)和圖(c)采用的窗寬依次為h=n-1/2.5,h=n-1/3和h=n-1/4.

不妨將回歸2稱為虛假回歸,回歸3稱為真實回歸.圖2顯示,虛假回歸的擬合優度幾乎均勻分布在(0,1)的區間里,而真實回歸的擬合優度集中在1附近.在隨機趨勢的影響下,雖然z與y之間不存在關聯關系,但有時會得到不錯的擬合優度.擬合優度指標是失效的.窗寬的不同沒有造成顯著的差異.

研究還做了另一組實驗.令k=10,即放大被解釋變量的波動幅度,比較真實回歸與虛假回歸的擬合優度,結果見表1.

根據實驗設定可知,用z來預測y既沒有經濟意義,又沒有實用價值.但當因變量有較大波動幅度時,有超過5%的概率,偽回歸的模型看上去更有效.如果單純依據擬合優度選擇模型,有5%以上的概率誤選偽回歸的模型做分析和預測.

圖2 回歸2和回歸3的擬合優度經驗分布圖Fig.2 Empirical distribution of goodness of fit for regression 2 and regression 3

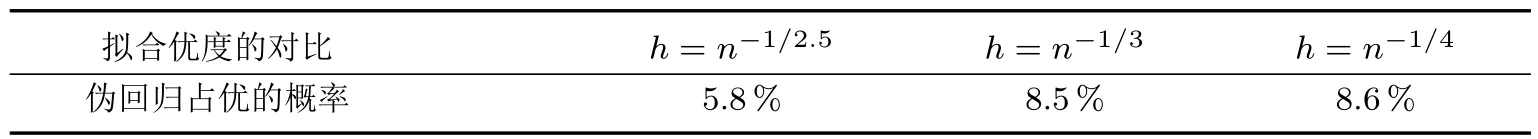
表1 憑擬合優度選解釋變量時犯錯的概率(k=10)Table 1 The probability of choosing wrong when explanatory variables are selected by goodness of fit(k=10)

可以得到一個初步的結論,對非平穩數據做非參數回歸時,擬合優度指標無效.模型需要新的診斷工具來識別虛假的回歸.

3 基于殘差特征的模型診斷方法

當數據生成過程存在隨機趨勢時,擬合優度指標不再可靠,DW統計量變得重要.無論是參數模型還是非參數模型,都對殘差序列做了“相互獨立”的假設.如果估計出的殘差違背了獨立性的假設,對模型的估計可能存在失真.反過來看,若模型設定有誤,所估計出的殘差通常存在序列相關.利用DW指標對殘差做檢驗,可以幫助識別這類模型.

存在偽回歸問題的參數模型,具有三個特征,分別是異常的關聯關系、較高的擬合優度和極低的DW統計量.對參數模型的偽回歸診斷,主要是借助DW統計量對殘差做序列相關檢驗.若DW統計量存在異常,可以推斷模型存在虛假回歸.

非參數殘差的形成機制有所不同.非參數回歸是一種逐點估計,局部與局部之間缺乏關聯.但對點估計和局部估計而言,仍可以用殘差的函數來描述估計面臨的風險.不同位置的殘差應當具有不同的影響權重.為了評價估計所面臨的風險以實現對非參數模型的診斷,需要基于DW統計量的思想,設計新的統計量.下面基于非參數核回歸模型,研究殘差特征與估計風險的關系,給出偽回歸檢驗的設計思路和理論依據.

3.1 非參數核回歸的模型設定

非參數回歸的一般形式為[11]

其中x為解釋變量,y為被解釋變量,t為誤差項的估計值,是對被解釋變量的核回歸估計,其形式為

其中K(·)是核函數,h為窗寬.

在非參數模型當中,窗寬的選擇對模型的估計有顯著的影響.當窗寬取無窮大時,非參數模型退化成線性參數模型；當窗寬無窮小時,非參數模型研究的是極小區間內的關系,甚至可能會濃縮到一個點.對偽回歸的診斷,就有逐點視角、局部視角和全局視角等三個角度.全局視角的分析與參數模型一致,下面主要討論“逐點視角”和“局部視角”.

3.2 非參數點估計的風險及偽回歸殘差特征

非參核回歸所做的點估計,本質上是用多個觀測值的加權平均來估計被解釋變量,可將該估算方法的表達式改寫成

其中wt,i表示估計yi時yt所占的權重,其表達式為

在x與y間函數關系連續的假設下,如果觀測點的x取值相鄰,其y的取值也應該相鄰；若xi與xj的差在約定的范圍內,對任何i?j,都可以用yj作為估計yi的參考；若xi與xj的觀測值足夠臨近,yj與yi也該接近,所以yj將被賦予較高的權重.當數據存在異常值時,加權平均的方法不再適用.舉一個極端的例子,設yi是一個顯著的離群值,以至于它與其它y觀測值的差別很大,而其它y觀測值之間的差別小到可以忽略,就不應該用y的加權平均值當作yi的估計值.以yj來估計yi是存在風險的,不同位置帶給估計的風險具有不同的權重.

非參數模型的點估計風險可以用級數來描述,其表達形式為

在這個級數中,如果相鄰數項相關系數為1,點估計值不會隨著樣本容量的增加而收斂,估計風險將失控.在wt,i(yi-yt)序列存在高度關聯的特征時,模型的估計是不可靠的.前人的研究主要關注隨機趨勢給殘差特征帶來的影響.本文特別關注殘差數據特征和回歸可靠性之間的關系,并將回歸風險的診斷問題轉化成級數收斂的檢驗問題.

3.3 局部的非參估計風險及對應的殘差特征

對點估計風險的檢驗,需要檢驗wt,i(yi-yt)序列的相關特征,這要求yi為已知量.然而在實際預測工作中,待預測的觀測值通常是未知量.診斷對某個待預測點的非參估計,需要引入“局部視角”,也就是以該點為觀察點,考察對估計該點產生影響的整個局部,診斷非參數回歸在這個局部的表現.在這個局部里,各位置的i都需要考慮進來.

定義一個待預測點(xobs,E[y|xobs]),因變量的非參估計值為

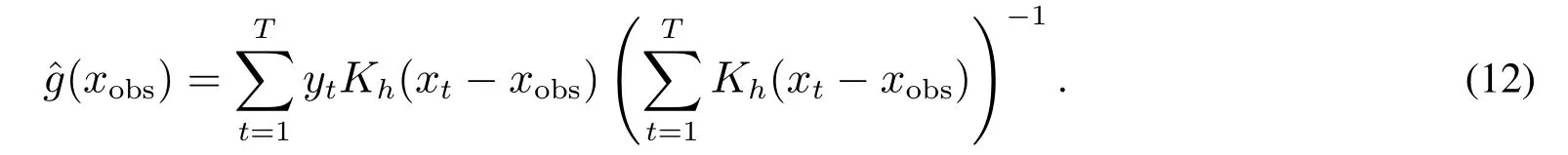
根據定義,待預測點的y為E[y|xobs],可以將估計風險定義成估計值的偏差,并可表達為

判斷一個局部的回歸質量,要考察回歸在局部范圍內每一處的估計風險.從觀測點的角度出發,不同位置的風險應該被賦予不同的權重.用加權的思想設計局部DW檢驗,可以識別這種風險.從另一個角度來看,檢驗wt,obst的序列相關特征,可以看成檢驗t序列是否滿足獨立性假設的一種非線性方法.

3.4 殘差序列相關特征的識別

經過上面的研究,已經把回歸風險的診斷問題轉化成了殘差性質的診斷問題.在研究非參數回歸殘差診斷之前,首先回顧參數模型的情況.

DW統計量是檢驗參數模型殘差性質的重要工具,其表達式為

其中T為樣本容量.

使用參數模型研究問題,最終會給出確定的模型形式及內部參數的估計值,以表述在全部定義域內解釋變量如何影響被解釋變量.模型每一處的殘差都有平等的地位,在構造統計量時擁有相同的權重.對非參數回歸模型的診斷,則有所不同.非參數模型中沒有一個代表全局的表達式可供診斷,不同局部間的關聯性隨間隔變大而變弱.診斷特定局部的回歸時,其它位置的殘差不再具有平等的地位.Phillips[6]基于相似的思想,率先定義了局部擬合優度和局部DW,其表達式分別為

對一組無關非平穩序列做非參數回歸時,局部DW統計量在h→0且Th→∞的假設下有穩定的漸進分布(參見文獻[6]中的定理3),可以很好地描述變量趨勢帶給模型的殘差特征.模型如果具有這種殘差特征,其估計的過程就會存在風險,因此局部DW檢驗可以用來診斷模型的虛假回歸.

當數據存在隨機趨勢,擬合優度指標不再可靠時,局部DW統計量直接用殘差擬合值構造函數,相當程度上減弱了觀測值非平穩帶給檢驗統計量的干擾.其背后的原理在于,加權后的殘差可以更恰當地描述非參數模型所面臨的回歸風險.局部DW統計量所發現的殘差相關性,已經不再是簡單線性相關關系,而是非參數意義上的相關關系.

綜上所述,可以依據殘差存在的這種非線性序列相關性來推斷非參數模型估計存在的風險；局部DW統計量可以識別這種序列相關,進而幫助識別模型的誤設；統計量在漸進意義上是可靠的.實際的數據分析工作中,討論統計量在漸進意義上是否有效固然重要,其漸進速度同樣對檢驗的實際應用產生重大影響.下面通過模擬實驗,研究實際應用當中,局部DW統計量能否有效地診斷出非參數模型中的偽回歸問題.

4 模擬實驗

通過模擬實驗評估局部DW檢驗在非參數模型中的表現.實驗的目的在于,一方面評估局部DW檢驗在非平穩數據非參數回歸中識別偽回歸的功效,為理論提供支持；另一方面估算恰當的統計量拒絕域,為實際研究提供參考.考慮到非參數回歸有樣本容量T和窗寬h兩個重要的參數,實驗對不同樣本容量和不同窗寬分別做了考察,試圖發現局部DW統計量如何隨模型參數變化而變化.

生成隨機序列xt、yt和zt,序列生成方式與前文中的x、y和z相對應.yt與xt存在穩定的關聯關系,而與zt無關.序列均存在隨機趨勢,波動幅度參數k=1.用前文中的回歸2和回歸3對yt做回歸分析,用局部DW檢驗對回歸做診斷,在實驗中觀察檢驗的表現.在實驗之前,需要對核函數的形式做預設.在非參數回歸當中,通常要根據數據關聯關系來選擇核函數,實驗選用了常見的正態核函數.在檢驗當中,需要借助核函數來排除局部間的干擾,因此在計算局部DW統計量時,原則上不可以使用正態核,實驗選擇了較簡單的均勻核.如何更恰當地選擇核函數,有待進一步的研究.

原假設為H0:模型的解釋變量與被解釋變量存在關聯關系.備擇假設為H1:模型錯誤地選擇了無關的解釋變量.

回歸3使用x做自變量,原假設H0成立.對這類回歸做檢驗,應該以極小的概率拒絕H0(犯棄真錯誤的概率較小),同時以較大的概率拒絕H1(犯取偽錯誤的概率也較小).回歸2使用z做自變量時,備擇假設H1成立.對這類回歸做檢驗,應該以較大的概率拒絕H0,以較小的概率拒絕H1.運用模擬數據,分別計算兩組回歸中的局部DW指標,結果見圖3,

圖3 回歸2和回歸3在中位點附近的局部DW統計量經驗分布圖Fig.3 Empirical distribution of local-DW-statistics near the median site of regression 2 and regression 3

圖3中從左到右的三條曲線分別對應三組不同的實驗,圖(a),圖(b)和圖(c)采用的窗寬依次為h=n-1/2.5,h=n-1/3和h=n-1/4,每組實驗重復1 000次.觀察圖3可知,回歸2的局部DW統計量取值集中在0附近,而回歸3的局部DW統計量取值集中在2附近.數據的隨機趨勢并沒有給局部DW統計量的表現帶來干擾.

繼續借助實驗研究局部DW統計量的檢驗臨界值.采用n-1/2.5、n-1/3和n-1/4三個窗寬,選擇1/4分位點、中位點和3/4分位點為回歸檢驗的觀測點,劃定三個“待觀測局部”,選擇T=100,500,1 000,三個樣本容量.首先考察中位點附近,局部DW檢驗的表現,實驗結果見表2.

表2 中位點附近做局部DW檢驗時回歸落入拒絕域的概率表Table 2 Probability table of falling into the rejection domain when local DW test is performed near the midpoint

在中位點診斷非參數模型,局部DW檢驗的功效較好.尤其是在局部數據足夠多時(即窗寬大、樣本多時),局部DW統計量可以顯著地區分真實回歸和虛假回歸.下面觀察1/4分位點和3/4分位點的情況,實驗結果見表3.

表3 分位點附近做局部DW檢驗時回歸落入拒絕域的概率表Table 3 Probability table of falling into the rejection domain when local DW test is performed near the locus

診斷1/4和3/4分位點的非參數估計,局部DW檢驗的功效有所下降.尤其是在小樣本、小窗寬的情況下,統計量分布不穩定.將棄真概率設置到0.01附近時,取偽概率普遍接近或超過0.1；當棄真概率設置到0.05附近,取偽概率的表現才有所改觀.當樣本容量超過500后,局部DW統計量分布趨于穩定,檢驗功效有所提高.

以上研究表明,局部DW檢驗可以較好地識別非平穩數據非參數回歸中的偽回歸.實驗發現,局部DW檢驗的功效呈現出一條基本規律,即有效樣本越多,檢驗功效越好.當樣本容量較小時(如T＜100),統計量波動尺度較大,檢驗的功效也較差；在大樣本下,檢驗功效普遍較好.窗寬越小(所容納的觀測值也就越少),檢驗的功效越差；當窗寬變大,檢驗功效將得到顯著提升.當樣本數據來自總體的邊緣,檢驗功效較差；而對中位點附近的非參估計做診斷,檢驗功效較好

5 結束語

本文對非參數模型中的偽回歸診斷問題進行了研究.與參數模型相似,非參數模型同樣可能發生偽回歸.通過研究非參數核回歸的估計風險與殘差特征發現,模型的估計風險可以表述成級數部分和的形式,而殘差序列中特定的相關特征會造成級數的發散即模型估計風險的失控；用加權后殘差構造的局部DW統計量,可以檢驗這種序列相關.這些論證為使用局部DW檢驗方法來預警回歸風險和診斷虛假回歸提供了堅實的理論依據.模擬實驗發現,局部DW檢驗具有良好的功效.在原假設成立和備擇假設成立兩種情況下,局部DW統計量都可以較快地趨近于對應的穩定分布.應用局部DW檢驗時,可根據實際的樣本容量和窗寬設定來參考本文中相應的統計量臨界值.