納米多孔銀力學性能表征分子動力學模擬?

李杰杰 魯斌斌 線躍輝 胡國明 夏熱2)

1)(武漢大學動力與機械學院,水力機械過渡過程教育部重點實驗室,武漢 430072)

2)(武漢大學動力與機械學院,水射流理論與新技術湖北省重點實驗室,武漢 430072)

(2017年10月10日收到;2017年12月13日收到修改稿)

1 引 言

納米多孔金屬(nanoporous metals,NPMs)是一類具有高比表面積、納米級孔棱直徑和三維雙連續微結構的新型功能性材料,兼具了傳統多孔材料的結構特征以及納米材料的優異性能.獨特的微結構特征以及優良的物理、化學性能,賦予了納米多孔金屬在催化劑[1,2]、傳感器[3]、執行器[4]、儲能[5]、電化學驅動等[6,7]領域極大的應用潛力.而對其力學性能的研究和掌控,是推動納米多孔金屬功能化應用和發展的關鍵因素之一.

納米多孔材料的相對密度、孔棱尺寸、拓撲幾何結構等參數是決定其力學性能的重要因素,成為當前力學性能實驗、理論及仿真研究的主要關注點之一.對于宏觀孔隙結構的材料,Gibson和Ashby[8]給出了多孔固體力學模型和變形機理,涵括多孔材料的彈塑性形變、脆性坍塌、壓縮變形等,定義了多孔材料力學性能隨其幾何參數變化的標度律.Liu等[9,10]探究了多孔材料在壓縮載荷作用下的屈曲失效和剪切破壞模式.Diwu等[11]分析了多孔金屬的應力應變關系及其位錯發展規律.在納米多孔材料研究中,Jin等[12]和Liu等[13]研究得出材料微結構是其力學性能的重要影響因素之一;發現實驗制備的納米多孔金樣品的強度與硬度低于Gibson-Ashby標度律的預測值,并將這一現象歸結于納米多孔金樣品中較低的孔棱連接性,同時引入有效相對密度概念,優化了Gibson-Ashby提出的有關強度與硬度的標度律,為合成高強度、高硬度的納米多孔材料提供了思路.Zabihzadeh等[14]研究了納米多孔多晶銀的強度與孔隙率之間的相關性.Volkert等[15]通過納米多孔金的單軸壓縮實驗分析納米多孔金的力學性能,發現多孔材料的密度、結構以及孔棱和胞壁的絕對尺寸是影響材料力學性能的重要因素.Mangipudi等[16]將亞穩態分解過程形成的隨機雙連續結構、螺旋結構與真實納米多孔金的整體力學性能進行對比,探究了拓撲結構和形態結構對標度律的影響.

然而,在現行納米多孔金屬力學性能分析中,理論及仿真所采用的模型各異,包括立方胞元模型[17]、球棍模型[18]、螺旋體模型[19]和隨機雙連續模型等[20].明晰不同微結構特征對力學響應的狀態差異,以及模型選用對變形結果分析的影響趨勢,將有助于建立更為統一、合理的力學分析體系.同時,通過調控幾何結構使材料的力學性能達到最優是力學超材料的主要設計理念,而具有周期性結構的多孔銀可視為力學超材料的一種,因此,基于Li和Gao[21]提出的“越小越強”的設計理念,探討納米尺度下微觀拓撲結構對力學性能的影響,對于設計力學性能最優的納米多孔金屬具有重要指導意義,也將進一步推進其功能化應用.

基于此,本文采用分子動力學方法,分析了納米多孔銀(nanoporous sliver,NPS)在單軸拉伸載荷下的力學響應,著重考察了模型的拓撲結構差異引起的力學特性變化,并闡述了納米多孔銀力學性能對幾何拓撲結構的依賴關系,在此基礎上初步探討了相對密度對其力學性能的影響.

2 模擬方案

2.1 模型建立

為分析相對密度對力學性能的影響,三種結構均取ρ=0.30—0.50之間五組不同相對密度值.相對密度ρ=ρ?/ρb定義為孔棱處原子數與全體積原子總數的比值,其中ρ?為納米多孔材料的密度,ρb為塊體材料的密度.三種結構的基體尺寸均取80a0×80a0×80a0,其中a0為銀的晶格常數(a0=4.0898 ?,1 ? =0.1 nm).

圖1 納米多孔銀3×3×3胞元結構(a)立方體結構;(b)金剛石結構;(c)螺旋體結構Fig.1.Assemblies of 3×3×3 unit cells of NPS:(a)Cube structure;(b)diamond structure;(c)gyroid structure.

在納米多孔材料的研究進程中,基于立方胞元結構的研究為力學性能理論推導做出了巨大貢獻[8,17].立方體多孔模型是在正六面體基礎上,去除xyz三個方向中心對稱的矩形柱得到最小重復單元,再利用最小重復單元3×3×3列陣得到.通過改變去除的矩形柱尺寸來控制立方體結構的相對密度,圖1(a)為相對密度ρ=0.39的立方體結構納米多孔銀模型.

三重周期最小曲面(triply periodic minimal surface,TMPS)廣泛應用于機械、化學、物理等造型研究,也為多孔結構模型的建立提供了基礎[22].金剛石結構和螺旋體結構基于TMPS數學模型建立[23],由如下三角函數方程控制:

式中t為常數,用來控制相對密度大小;x,y,z為三個坐標方向;l為立方體晶胞邊長.定義?＞0部分為實體部分,?＜0部分為孔隙部分,?=0為實體部分與孔隙部分之間的分界面.圖1(b)為相對密度ρ=0.40的金剛石結構納米多孔銀模型;圖1(c)為相對密度ρ=0.40的螺旋體結構納米多孔銀模型.

2.2 計算方法

選用EAM(embedded atom method)勢能函數[24],利用經典的分子動力學軟件LAMMPS[25]開展納米多孔銀模型的單軸拉伸力學性能模擬.模擬過程中,運用Velocity-Verlet算法進行牛頓運動方程的數值積分,x,y,z三個方向均采用周期性邊界條件,時間步長設為1 fs.加載前,所有模型采用共軛梯度法進行能量最小化,然后在等溫等壓(NPT)系綜下使用Nosé-Hoover熱浴使系統在300 K恒溫條件下達到熱平衡.平衡后,對納米多孔銀平衡體系進行單軸拉伸模擬.

單軸拉伸過程中,常用的系綜為微正則(NVE)系綜[26,27]和NPT系綜[28,29],部分采用正則(NVT)系綜[30].NVE系綜下,體系能量保持不變,施加的單軸拉力對系統做功,相應原子的動能減少以抵消功的增加,從而保持系統能量恒定.拉伸過程中,系統縱向截面不發生變化,且溫度有所下降,如果溫度下降過快,材料將會發生脆斷,應力應變過程較為接近實際情況.NPT系綜下,在施加一個單軸拉力的基礎上,再使用barostat來控制另兩個非拉伸方向的壓強為零,調整沿兩個非拉伸方向的應力為零,且縱向截面隨著拉伸方向均勻變化,不出現頸縮現象,整個模型在發生極大應變時仍未斷裂,與實驗中觀察的現象存在一定的差異,不利于分析變形破壞機理.NVT系綜下,在變形的同時利用thermostat保持溫度恒定,在單軸拉伸模擬中使用較少.

基于此,在每個加載步中,x方向以109s?1的恒定應變率進行單軸拉伸,施加0.1%的工程應變增量.考慮到NVE系綜下每個加載步后體系溫度有所下降,每次拉伸完成后用Nosé-Hoover熱浴在300 K的恒定溫度下使系統松弛1 ps,松弛結束后進行下一步拉伸,循環反復,直至模型完全斷裂.為減小熱擾動波動等系統變量的影響,將每個加載步中最后100 fs的結果進行平均來分析處理數據.在模擬分析中,使用開放性可視工具OVITO(open visualization tool)[31],基于公共近鄰分析法(common neighbor analysis,CNA)[32]分析納米多孔銀微結構的演化過程.

3 結果與分析

3.1 應力應變

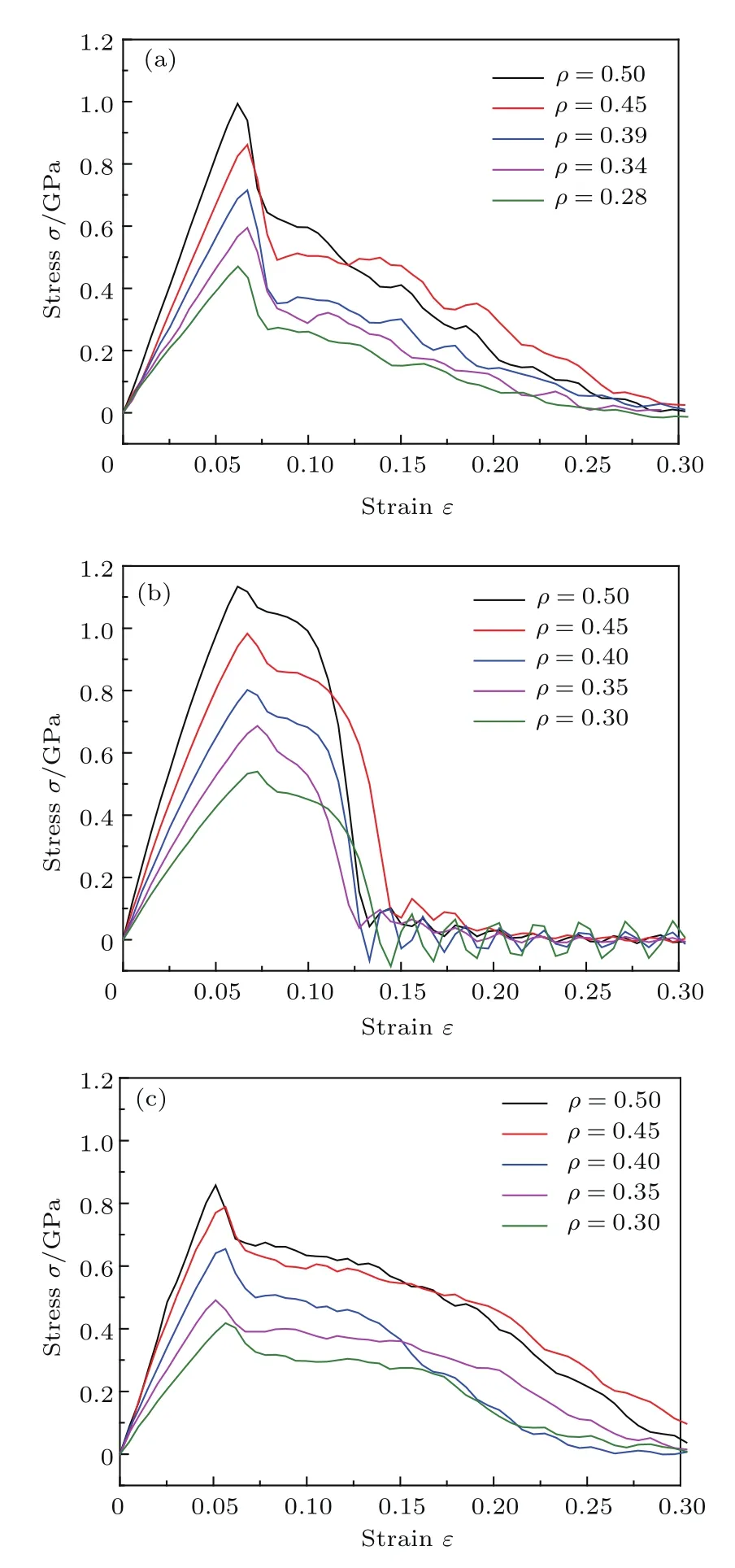
圖2 不同相對密度下的應力應變曲線 (a)立方體結構;(b)金剛石結構;(c)螺旋體結構Fig.2.Stress-strain curves of NPS with different relative densities:(a)Cube structure;(b)diamond structure;(c)gyroid structure.

圖2(a)—(c)分別為不同相對密度立方體結構、金剛石結構和螺旋體結構納米多孔銀在單軸拉伸載荷下的應力應變曲線.曲線由三個主要部分組成,第一階段為彈性形變區域,占整個應變過程較小一部分,應力隨著應變的增加而急劇升高直至極限應力,應力應變呈現線性關系,斜率為模型的楊氏模量Es;第二階段曲線進入塑性變形階段,應力隨著應變的增加而迅速降低,呈近似線性下降;最后階段,應力隨應變的增大而降低,下降速率減緩,此時,孔棱發生頸縮現象直至斷裂.

對于同一結構,隨著相對密度ρ的增加,極限應力σu不斷增大.如圖2(a)所示,立方體結構相對密度ρ從0.28增大到0.50時,極限應力σu從0.47 GPa增大到1.01 GPa,提升了114.9%.對于同一結構,在彈性應變階段,隨著相對密度ρ的增大,應力應變曲線不斷上移,表明楊氏模量不斷增加.如圖2(b)所示,金剛石結構相對密度ρ從0.30增大到0.50時,楊氏模量Es從7.86 GPa增長到19.17 GPa,增長了143.9%.分析可知,納米多孔銀與宏觀孔棱結構的多孔材料類似,基本力學性能在很大程度上依賴于相對密度.

3.2 變形行為

圖3—圖5分別為三種結構拉伸過程中拉伸方向的切片圖,可以看出三種結構的拉伸變化過程大體相似.為探討納米多孔銀的變形特征,以相對密度ρ=0.40時金剛石模型的切片為例,研究單個模型的變形行為,如圖4所示,其中原子按照共同近鄰原子法染色,灰色原子為表面原子,綠色原子為面心立方(face-centered cubic,FCC)原子,紅色原子為密排六方(hexagonal closepacked,HCP)原子.圖4(a)為模型初始狀態的形貌,經過平衡處理,模型中存在極少位錯.隨著應變的增加,開始產生少量位錯,HCP原子比例增加.在彈性階段,孔棱的變形是完全可逆的.圖4(b)中應變ε=0.062,此時存在大量HCP原子,納米孔洞的半徑開始增加,部分孔棱出現頸縮和層錯.但大部分孔棱依舊能夠承受載荷增長,此時材料表現為應力硬化行為,直至應力到達極限強度.應變ε=0.116時,HCP原子繼續增加,此時應力已經越過峰值,出現大量層錯及頸縮,模型即將從中間孔棱區域部分斷裂,如圖4(c)所示.隨著應變的增加,最弱的豎直孔棱首先被拉斷,導致模型凈截面積減小,孔棱的斷裂使應力重新分布,從而導致多孔材料連續變形和破壞.從圖4(d)可以看到,當應變達到0.221時,所有豎直的孔棱均有破壞.拉伸變形過程中,塑性變形主要由孔棱的屈服主導,破壞發生在孔棱區域.

圖3 立方體結構納米多孔銀單軸拉伸時原子的運動過程 (a)ε=0;(b)ε=0.062;(c)ε=0.209;(d)ε=0.391Fig.3.Atoms’movement in cube NPS under uniaxial tension:(a)ε=0;(b)ε=0.062;(c)ε=0.209;(d)ε=0.391.

圖4 金剛石結構納米多孔銀拉伸時的原子運動過程 (a)ε=0;(b)ε=0.062;(c)ε=0.116;(d)ε=0.221Fig.4.Atoms’movement in diamond NPS under uniaxial tension:(a)ε=0;(b)ε=0.062;(c)ε=0.116;(d)ε=0.221.

圖5 螺旋體結構納米多孔銀拉伸時原子的運動過程 (a)ε=0;(b)ε=0.062;(c)ε=0.209;(d)ε=0.310Fig.5.Atoms’movement in gyroid NPS under uniaxial tension:(a)ε=0;(b)ε=0.062;(c)ε=0.209;(d)ε=0.310.

圖6為螺旋體結構納米多孔銀拉伸過程的切片示意圖.圖6(a)為初始狀態,兩螺旋狀孔棱間夾角為111.5°;圖6(b)為應變ε=0.138時的切片圖,孔棱間夾角為120.1°,在拉伸過程中夾角變大,表明納米多孔銀在單軸拉伸變形過程中螺旋狀孔棱逐漸被拉直.對比分析可以看出,螺旋體結構的高應力平臺持續時間更久(圖2(c)),塑性更好.此現象與螺旋體結構中螺旋狀的孔棱有關,在單軸拉伸的過程中,螺旋形式的孔棱在受力拉直過程中抵抗變形,表現出較好的塑性.

圖6 不同應變下螺旋體結構納米多孔銀螺旋狀孔棱示意圖 (a)ε=0;(b)ε=0.138Fig.6. Schematics of the typical spiral ligament in gyroid NPS under different strains:(a) ε =0;(b)ε=0.138.

3.3 力學性能的標度律

Gibson和Ashby[8]系統研究了多孔材料的力學性能,給出多孔材料的楊氏模量與相對密度之間的標度律:

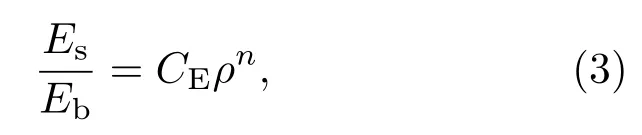
式中Es為多孔結構的楊氏模量;Eb為塊體模量,選用銀的塊體模量Eb=83 GPa[33];ρ為相對密度;CE和n為常數,大小取決于材料微結構,可以由實驗得到.由(3)式可知楊氏模量Es與相對密度ρ的關系為Es=aρn.

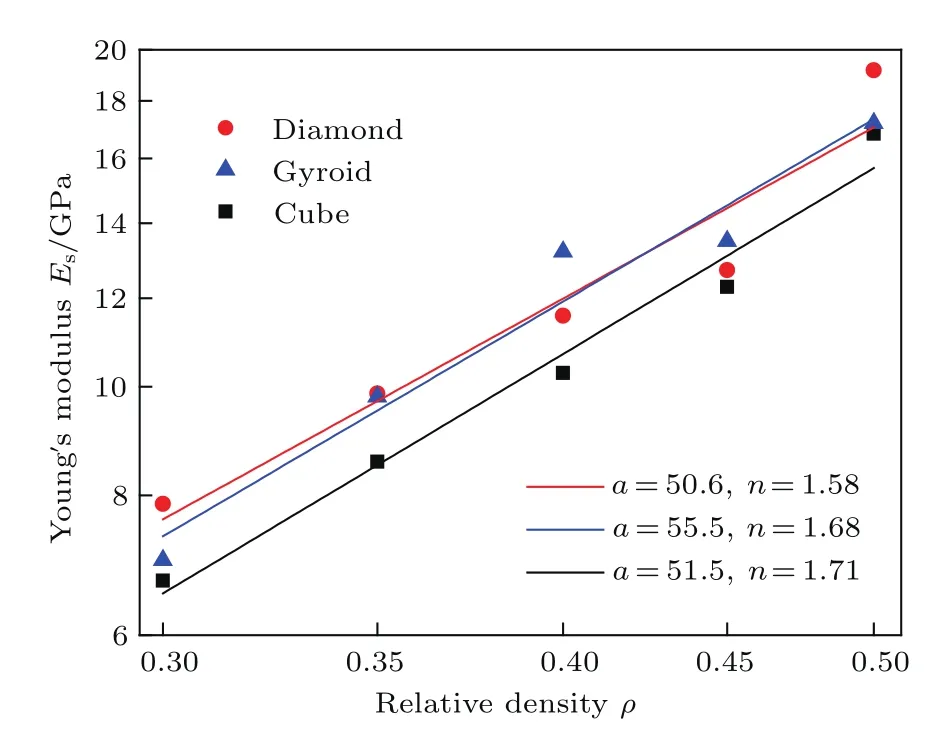
圖7 雙對數坐標下不同結構的楊氏模量與相對密度之間的擬合關系Fig.7.Fitting curves of Young’s modulus as a function of the relative density for different morphological architectures in double logarithmic plots.

圖7所示為三種結構在不同相對密度下楊氏模量Es的變化曲線圖,在雙對數坐標下,相對密度ρ與楊氏模量Es的擬合線為直線.根據擬合直線可得,立方體結構楊氏模量與相對密度之間滿足Es1=51.5ρ1.71;金剛石結構滿足Es2=50.6ρ1.58;螺旋體結構滿足Es3=55.5ρ1.68.Gibson-Ashby給出關于楊氏模量的標度律,只考慮彎曲變形不考慮拉伸的貢獻時,Es/Eb∝ρ2;考慮彎曲變形時,可以得到Es/Eb=(d/l)2,其中l為孔棱的長度,d為孔棱的直徑.同時,相對密度與孔棱的尺寸有幾何關系ρ∝(d/l)2,因此對于拉伸變形的貢獻有Es/Eb∝ρ.對于開孔多孔材料而言,當相對密度較低時,以彎曲變形為主導;相對密度較高時,主要是拉伸變形在控制.根據冪指數關系擬合了多孔銀模量與相對密度之間的關系,立方體結構的冪指數為1.71,金剛石結構的冪指數為1.58,螺旋體結構的冪指數為1.68,三者的值均介于1—2之間,表明在變形中既有彎曲變形也有拉伸變形.立方體結構和螺旋體結構的冪指數值較為接近,表明兩種結構變形過程中彎曲變形和拉伸變形的影響程度相近;金剛石結構的冪指數值較接近1,變形過程中拉伸變形的影響程度相對其他兩種結構稍大.由圖7可知,金剛石結構和螺旋體結構的擬合直線幾乎重合,兩者的楊氏模量大小和變化趨勢較為相似,原因在于兩者均由三重周期最小曲面構成,兩結構具有較高的相似性.同時,螺旋體結構和金剛石結構的楊氏模量大于立方體結構,主要是由于立方體結構簡單,孔棱形式單一,抵抗拉伸變形的能力較弱.由此可得出,同一相對密度下,拓撲結構是影響納米多孔銀楊氏模量的重要因素之一,孔棱分布復雜的結構比形式單一的結構抵抗變形的能力更強,模量更高.

圖8為不同模型的極限強度σu隨相對密度的變化曲線圖,強度與相對密度滿足線性關系.圖中直線為擬合直線,滿足公式σu=Bρ+C,其中B和C是待定常數.根據圖中擬合直線,立方體結構擬合參數B1=2.7,C1=?0.34;金剛石結構擬合參數B2=3.0,C2=?0.36;螺旋體結構擬合參數B3=2.4,C3=?0.31.對于單軸拉伸作用下的多孔材料,Gibson和Ashby指出其塑性變形主要來自兩種典型的變形機理,一是連接點處的塑性坍塌,二是孔棱的屈服.當連接點處的塑性坍塌主導時,強度與相對密度呈二次冪指數關系;當孔棱的屈服為主導時,強度與相對密度呈線性關系.三種模型的強度與相對密度呈線性關系,表明納米多孔銀的屈服行為主要為孔棱的屈服.從3.2節可以看出三種結構的納米多孔銀的塑性變形主要依賴于孔棱,破壞發生在孔棱處,這與上述擬合得到的結論一致.由圖8可以看出,在同一相對密度條件下,金剛石結構的極限強度最大,立方體結構次之,螺旋體結構最小.金剛石結構中存在大量相互交錯的孔棱,孔棱與孔棱之間形成類似三角骨架的結構,如圖9所示,該結構具有較好的穩定性,展現出相對高的極限強度.

圖8 不同結構的極限強度與相對密度之間的擬合關系Fig.8.Fitting curves of ultimate strength as a function of the relative density for different morphological architectures.

圖9 金剛石結構納米多孔銀三角骨架結構示意圖Fig.9.Schematic of triangular skeleton structure of diamond NPS.

4 結 論

納米多孔銀的極限強度和楊氏模量均隨相對密度的增大而增大.極限強度與相對密度近似為線性關系,塑性變形和破壞主要依賴于孔棱;楊氏模量與相對密度近似為冪指數關系,孔棱變形過程中不僅包含彎曲變形,還存在拉伸變形.

納米多孔銀的力學性能與拓撲結構具有緊密的相關性.螺旋體結構和金剛石結構均由三重周期最小曲面構成,結構存在一定的相似性,抵抗變形的能力相近,表現為模量值接近;立方體結構的孔棱形式單一,分布形式簡單,模量值較小.金剛石結構的孔棱交錯排列,形成類似三角骨架結構,塑性變形過程中具有一定的穩定支撐作用,表現出相對較高的極限強度.

螺旋體結構因存在螺旋形式的孔棱,在受力拉直的過程中抵消部分變形,表現出更好的塑性.

[1]Zhai X,Ding Y 2017Acta Phys.-Chim.Sin.33 1366(in Chinese)[翟蕭，丁軼2017物理化學學報 33 1366]

[2]Wittstock A,Zielasek V,Biener J,Friend C M,B?umer M 2010Science327 319

[3]Zhang L,Chang H,Hirata A,Wu H,Xue Q K,Chen M 2013ACS Nano7 4595

[4]Detsi E,Onck P R,de Hosson J T M 2013Appl.Phys.Lett.103 193101

[5]Ding Y,Zhang Z 2016Nanoporous Metals for Advanced Energy Technologies(Berlin:Springer Cham)pp83–131

[6]Ye X L,Liu F,Jin H J 2014Acta.Metall.Sin.50 252(in Chinese)[葉興龍,劉楓,金海軍2014金屬學報50 252]

[7]Jin H J,Wang X L,Parida S,Wang K,Seo M,Weissmüller J 2010Nano Lett.10 187

[8]Gibson L J,Ashby M F 1997Cellular Solids:Structure and Properties(2nd Ed.)(Cambridge:Cambridge University Press)

[9]Liu P S 2010Acta Phys.Sin.59 8801(in Chinese)[劉培生2010物理學報59 8801]

[10]Liu P S 2010Acta Phys.Sin.59 4849(in Chinese)[劉培生2010物理學報59 4849]

[11]Diwu M J,Hu X M 2015Acta Phys.Sin.64 170201(in Chinese)[第伍旻杰，胡曉棉 2015物理學報 64 170201]

[12]Jin H J,Weissmüller J 2011Science332 1179

[13]Liu L Z,Ye X L,Jin H J 2016Acta Mater.118 77

[14]Zabihzadeh S,van Petegem S,Holler M,Diaz A,Duarte L I,van Swygenhoven H 2017Acta Mater.131 467

[15]Volkert C A,Lilleodden E T,Kramer D,Weissmüller J 2006Appl.Phys.Lett.89 061920

[16]Mangipudi K R,Epler E,Volkert C A 2016Acta Mater.119 115

[17]Feng X Q,Xia R,Li X,Li,B 2009Appl.Phys.Lett.94 011916

[18]Huber N,Viswanath R N,Mameka N,Markmann,J,Wei?müller J 2014Acta Mater.67 252

[19]Pia G,Brun M,Aymerich F,Delogu F 2017J.Mater.Sci.52 1106

[20]Sun X Y,Xu G K,Li X,Feng X Q,Gao H 2013J.Appl.Phys.113 023505

[21]Li X,Gao H 2016Nat.Mater.15 373

[22]Abueidda D W,Al-Rub R K A,Dalaq A S,Lee D W,Khan K A,Jasiuk I 2016Mech.Mater.95 102

[23]Yoo D J 2011Int.J.Precis.Eng.Man.12 61

[24]Daw M S,Baskes M I 1984Phys.Rev.B29 6443

[25]Pavia F,Curtin W A 2015Model.Simul.Mater.Sc.23 055002

[26]Yuan F,Huang L 2012J.Non-Cryst.Solids358 3481

[27]Vu-Bac N,Lahmer T,Keitel L,Zhao J,Zhuang X,Rabczuk T 2014Mech.Mater.68 70

[28]Luo J,Shi Y 2015Acta Mater.82 483

[29]Shen X,Lin X,Jia J,Wang Z,Li Z,Kim J K 2014Carbon80 235

[30]Pedone A,Malavasi G,Menziani M C,Segre U,Cormack A N 2008Chem.Mater.20 4356

[31]Stukowski A 2010Model.Simul.Mater.Sc.18 015012

[32]Faken D,Jónsson H 1994Comp.Mater.Sci.2 279

[33]Smith D R,Fickett F R 1995J.Res.Natl.Inst.Stand.Technol.100 119