等邊單角鋼構件受彎橫向屈曲問題的探討

陳俊帆,曾二賢,吳海洋

(中南電力設計院有限公司，湖北 武漢 430071)

1 概述

角鋼構件由于受力明確、易安裝、便于加工運輸等優點，在通信塔、輸電線路、鋼結構廠房、橋梁以及桁架等多個領域得到了廣泛的應用。隨著特高壓鐵塔設計荷載越來越大，大規格、高強度角鋼得到了越來越多的研究和推廣應用。但對于角鋼作為受彎構件的橫向屈曲問題卻常被忽視。

我國的《鋼結構設計規范》(GB50017—2003)(以下簡稱鋼規)對軋制等邊角鋼的應用，給出了其作為軸心受力構件的軸心強度和受壓穩定性計算的相關條文，未提及其作為受彎構件橫向屈曲的問題。學者對于角鋼構件的研究多集中在壓桿的承載力和穩定計算，對角鋼受彎時的驗算尚鮮見于文獻。美國標準ASCE/SEI 10－15(以下簡稱美標)考慮外荷載偏心的不利影響會引起角鋼構件在側向發生橫向屈曲，對等邊單角鋼構件引入了橫向屈曲臨界彎矩的概念，考慮其作為受彎構件時的橫向屈曲驗算。

本文通過對不同規格的等邊單角鋼展開參數化分析，參考美標的屈曲彎矩驗算公式，引入橫向屈曲影響系數η，研究了考慮受彎橫向屈曲對角鋼構件臨界桿長的影響。并針對輸電鐵塔結構特點，給出了設計中考慮人重荷載時水平桿材的受彎驗算建議，供線路工程設計參考。

2 美標關于等邊單角鋼受彎的驗算

美標中認為由于外荷載未作用在角鋼截面的彎曲中心，當角鋼側向無支撐時應考慮其偏心引起的構件橫向屈曲問題，因此引入橫向屈曲臨界彎矩的概念，在等邊單角鋼構件的受彎驗算中同時給出了橫向屈曲和應力強度的驗算公式。下面對其計算原理進行介紹，圖1為等邊單角鋼截面的荷載作用示意圖。

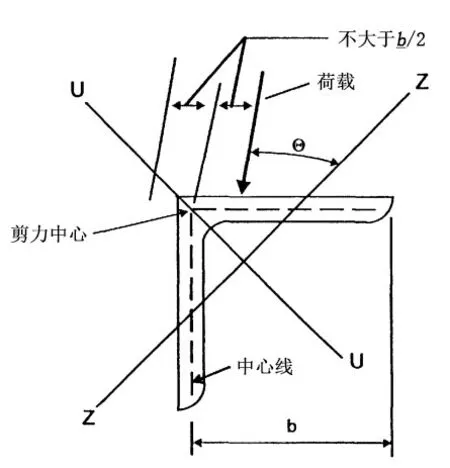
圖1 荷載作用于角鋼

2.1 橫向屈曲驗算

引入橫向屈曲臨界彎矩Mb：

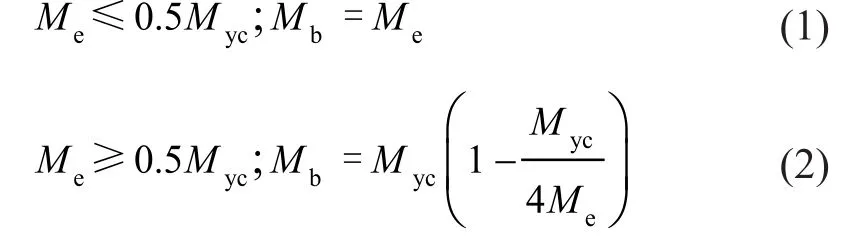
式中：Myc為截面端部最大屈服應力計算出的彎矩；Me為彈性臨界彎矩。

Me的取值，應按下式進行計算。對于荷載垂直于肢面的情況按式(3)計算：

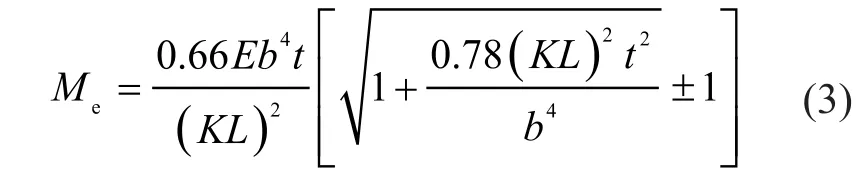
當荷載方向與Z軸夾角為θ時，按式(4)計算：

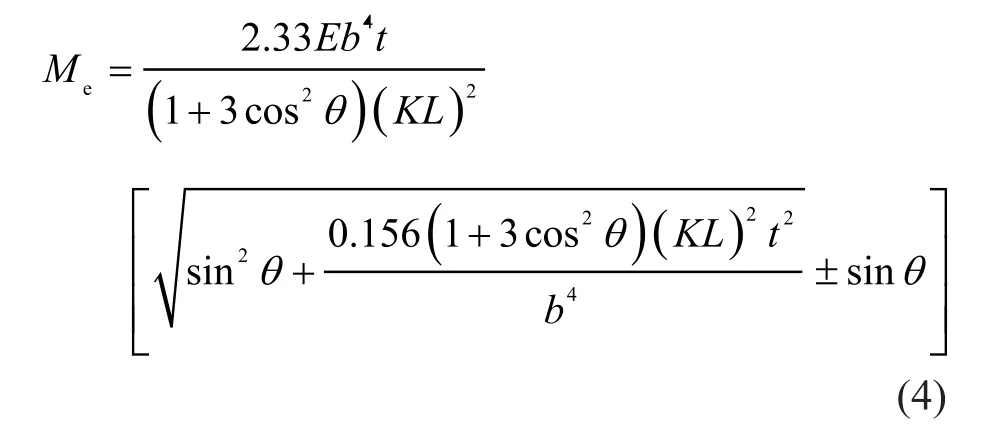
式中：E為彈性模量；b為肢寬－t/2；t為肢厚；L為側向無支撐長度；K為兩端簡支時，取1.0；兩端固結約束轉動時，取0.5。

式(3)、(4)中的±號，當荷載作用方向與圖1相同時，取“+”號；當荷載作用方向與圖1相反時，取“－”號。

2.2 強度驗算

肢跟處應力：

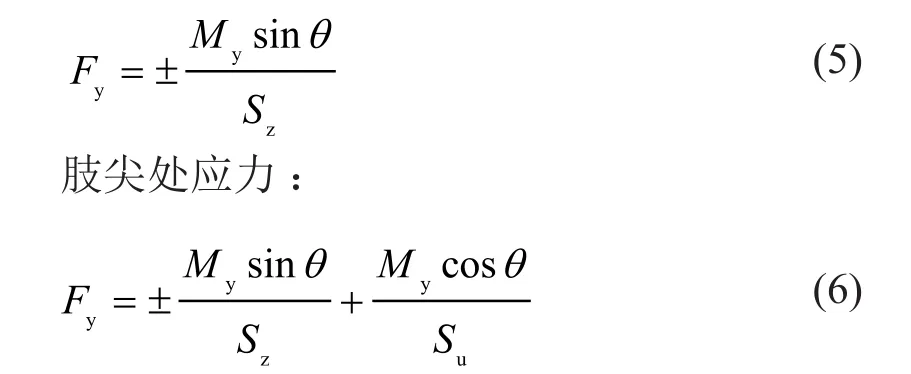
式中：Fy為鋼材的屈曲應力；Su和Sz分別為對于u軸和z軸的截面抵抗矩。其中±表示，拉應力為“+”，壓應力為“－”。截面抵抗矩按下式計算：

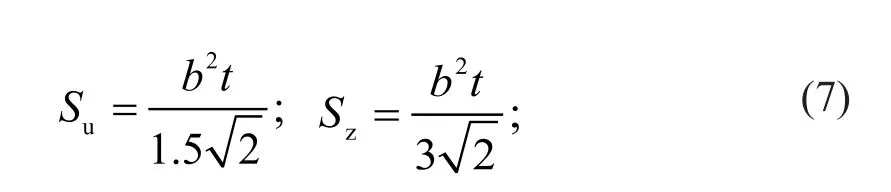
3 考慮橫向屈曲問題的影響

工程設計中，設計者通常只需驗算角鋼受彎考慮橫向屈曲后桿件的長度是否滿足要求。本文參考美標中對等邊單角鋼構件受彎的應力強度和橫向屈曲驗算，引入橫向屈曲影響系數η，參數化分析考慮橫向屈曲對臨界桿長的影響。在這里定義影響系數η：

其中，構件的臨界長度Lcr是指角鋼截面最大應力等于材料強度屈服值時對應的構件長度，考慮橫向屈曲的臨界長度可結合式(4)按下式計算得到：

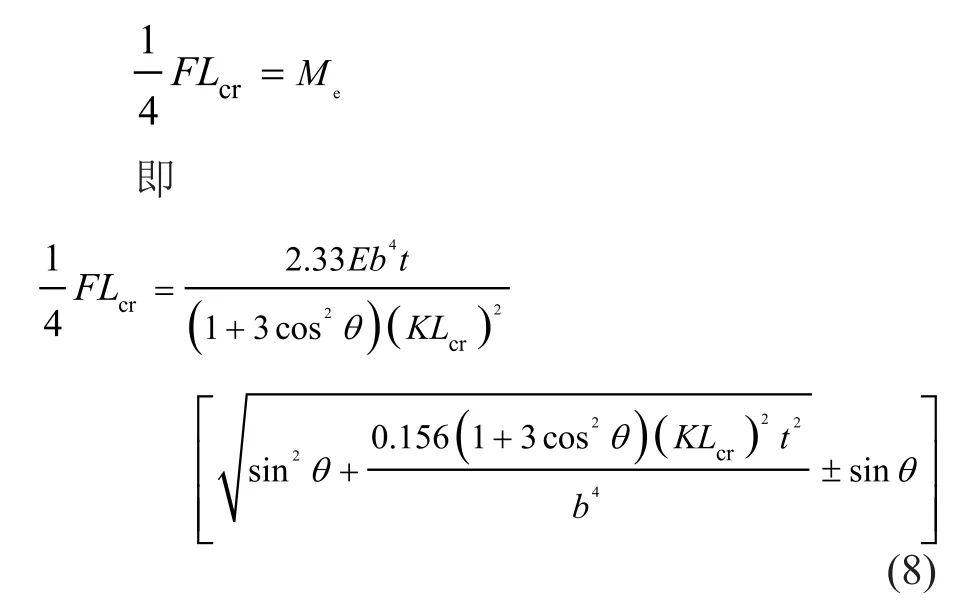
式中：F為集中外荷載。

需注意的是，對于給定的集中荷載，式(8)為一元多次方程，直接求解較為困難，本文建議采用迭代法進行臨界長度Lcr的求解。

算例分析中，角鋼構件按兩端簡支的等邊單角鋼考慮，鋼材強度按美標取材料強度的屈服值進行參數化分析。角鋼規格選取L40×3～L80×7，荷載方向按垂直于肢面考慮，即圖1中θ=45°，計算桿件臨界長度時，按集中荷載作用于桿長1/2處的最不利情況考慮。

3.1 集中荷載與影響系數η的關系

由于單角鋼構件在其U－U軸和Z－Z軸方向上的截面抵抗矩不同，因此強度驗算分別要求肢跟處和肢尖處截面的應力不超過鋼材的屈服強度，由此計算出的桿件臨界長度不同。為分析集中荷載對等邊單角鋼構件受彎橫向屈曲的敏感度影響，引入橫向屈曲影響系數η，計算對比了集中荷載分別取1000 N、1500 N和2000 N時橫向屈曲對臨界長度的影響趨勢，計算結果分別見表1～表3。

表1 集中荷載1000N時不同規格角鋼的臨界長度

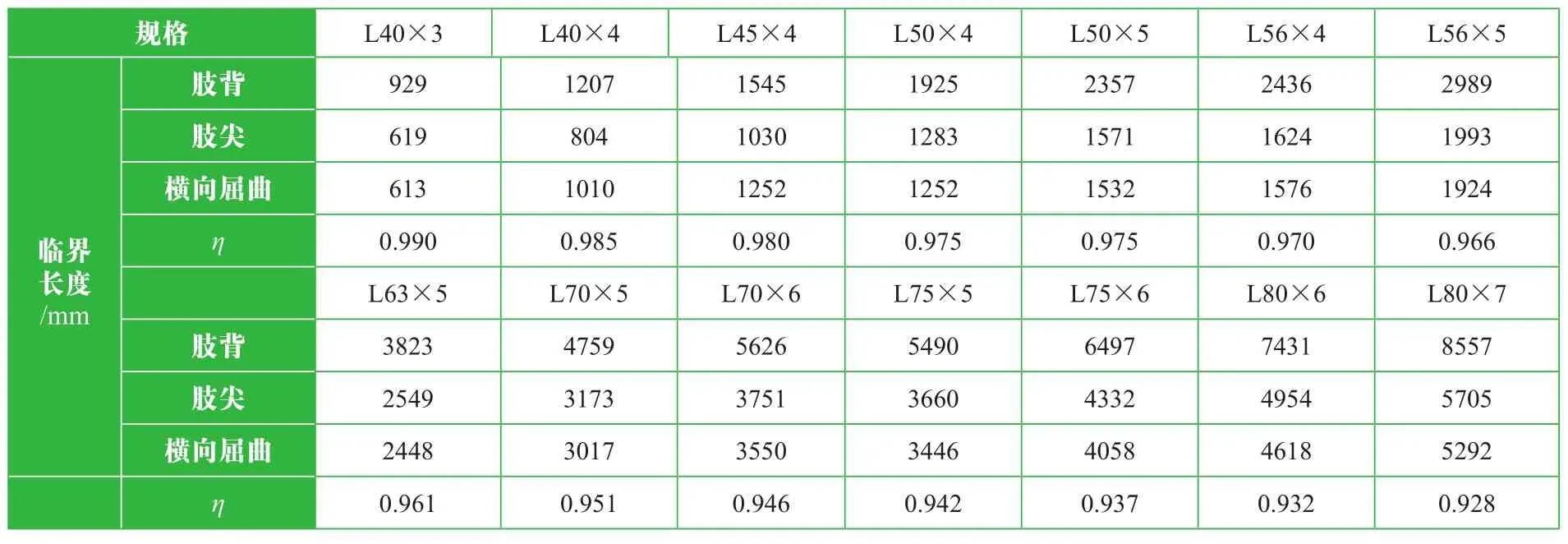
表2 集中荷載1500N時不同規格角鋼的臨界長度

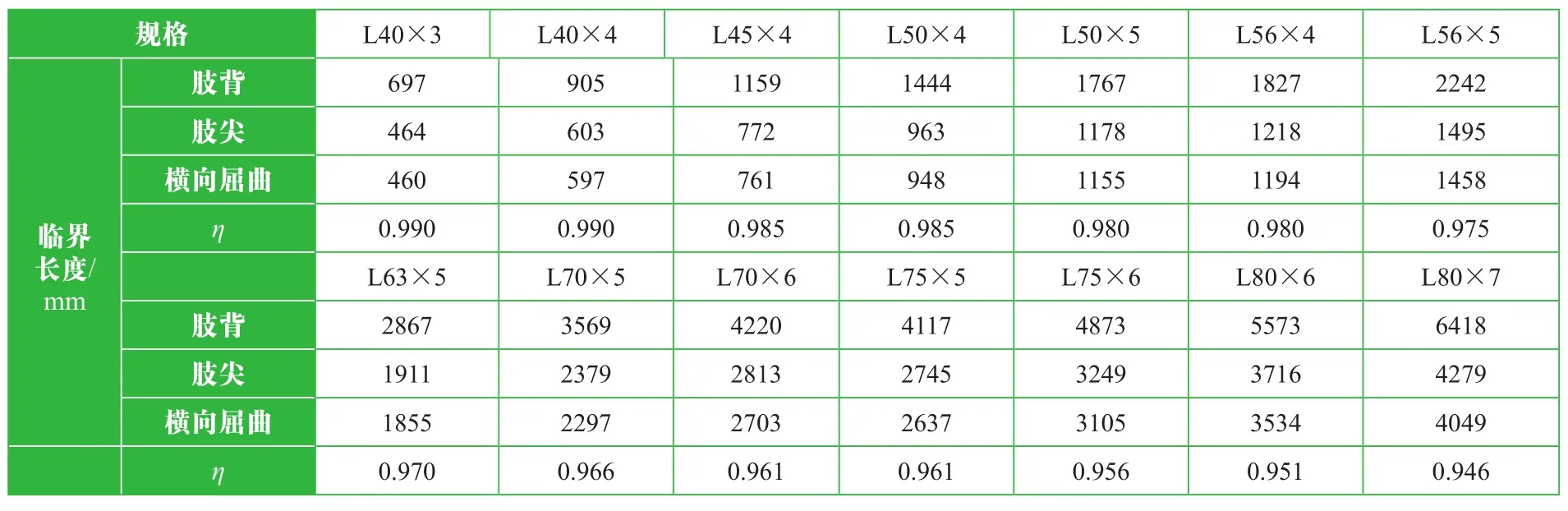
表3 集中荷載2000N時不同規格角鋼的臨界長度

從表中易看出，等邊單角鋼構件受彎強度驗算時，肢尖處的應力最大，會首先達到材料的屈服強度，其強度的臨界長度由肢尖處應力控制。考慮受彎的橫向屈曲后，臨界長度減小，且隨著角鋼規格的增加，其臨界長度折減越多。將作用不同集中荷載時，橫向屈曲影響系數與角鋼規格的關系進行對比分析，研究集中荷載對臨界桿長的影響，見圖2。

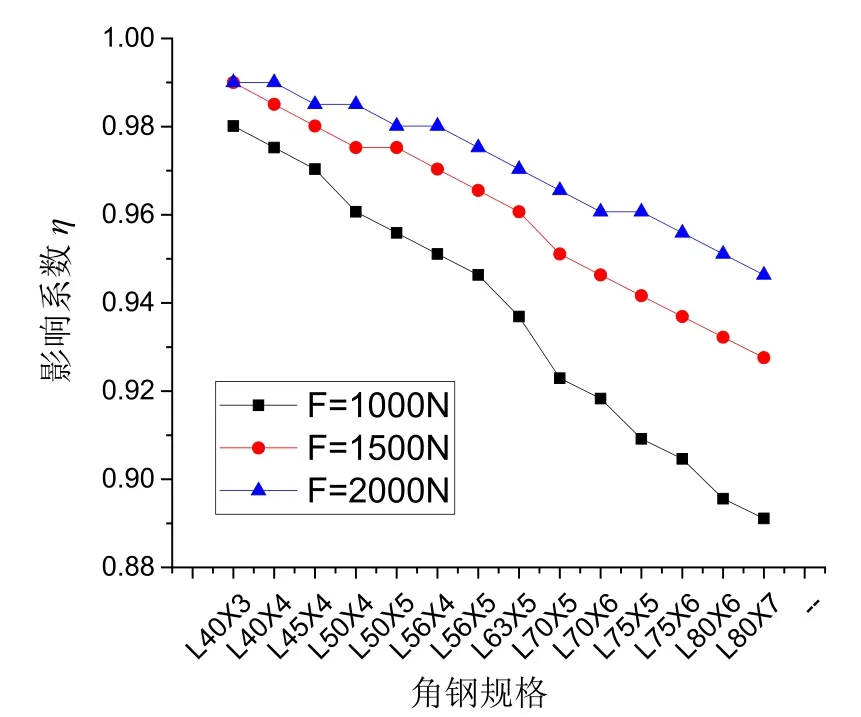
圖2 集中荷載對臨界桿長的影響

從圖2可以看出，隨著角鋼規格的變大，考慮橫向屈曲對構件臨界長度的影響越來越大。對于不同的集中荷載情況，橫向屈曲對角鋼構件臨界長度的敏感程度不同，集中荷載越小，曲線的斜率越大，其考慮橫向屈曲的臨界長度折減越多。其中L80×7角鋼對應集中荷載1000 N時，考慮橫向屈曲其臨界長度最多減小了11%。

3.2 鋼材強度與影響系數η的關系

針對高強度鋼材的應用越來越多，高強角鋼構件在實際工程中的應用也越發廣泛。下面考慮鋼材強度對構件臨界長度的影響，集中荷載取F=1000 N，此時等邊單角鋼構件的橫向屈曲問題較為顯著。

圖3 鋼材強度對臨界桿長的影響

從圖3可知，隨著鋼材屈服強度的提高，影響系數曲線下降斜率越來越大，等邊單角鋼構件的受彎橫向屈曲問題更為顯著。與Q235鋼材的影響系數曲線相比，Q345鋼材平均下移了約7%，Q460鋼材下移了約15.4%。其中Q460的L80×7規格角鋼桿件，在考慮橫向屈曲后臨界長度減小了約35%。因此，對于較大規格的高強度角鋼受彎驗算建議考慮橫向屈曲的不利影響，否則構件安全無法保證。

3.3 架空輸電線路設計的相關建議

在架空輸電線路中，格構式塔架廣泛采用等邊角鋼，在導地線掛點處的角鋼構件以及塔架結構中的部分構件考慮施工人重、設備等集中外荷載作用需進行受彎驗算。《架空輸電線路桿塔結構設計技術規定》(DL/T5154—2012)(以下簡稱國標)規定塔架中水平或接近水平(與水平面夾角不大于30°)的構件應在任意點考慮1000 N人和工具荷重，按集中荷載的簡支梁進行受彎驗算。此外，在實際工程及試驗中也多次證明，輔助材的屈曲會導致主材的失穩破壞，直接對鐵塔結構的安全性造成不利影響。

為研究橫向屈曲問題對架空輸電線路等邊單角鋼構件受彎驗算的影響，本文在按國標進行人重驗算時，增加了按美標考慮橫向屈曲驗算的對比研究，計算的臨界桿長見圖4。需注意的是，計算時國標采用材料強度設計值，美標采用材料強度屈服值。

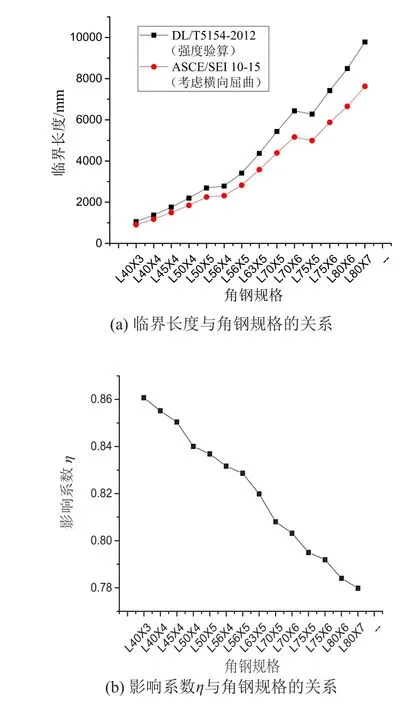
圖4 考慮橫向屈曲η對國標人重驗算的影響

在圖4給出的角鋼規格范圍內，進行等邊單角鋼構件人重受彎驗算時，即使國標在材料強度上考慮抗力分項系數取設計值，但按美標考慮橫向屈曲的不利影響后，臨界長度減小了14%～22%。設計實踐中表明，人重驗算通常對細長的輔助材起控制作用，而此類構件通常應力比較小，未能得到設計人員足夠的重視。

4 結論

通過計算分析等邊單角鋼構件的受彎橫向屈曲承載力，給出了考慮橫向屈曲對構件臨界長度的影響規律，重點考察了角鋼規格及材質、集中荷載大小等因素的影響。主要結論如下：

(1)角鋼規格越大，橫向屈曲影響系數η越小，在L40×3～L80×7角鋼規格范圍內，對應集中荷載為1000 N時，受彎驗算考慮橫向屈曲其臨界桿長最多折減11%。

(2)集中荷載越小，鋼材強度越高，單角鋼受彎臨界長度的橫向屈曲問題越顯著。

(3)對Q235級L80×7規格以下等邊單角鋼進行人重驗算時，按美標考慮受彎橫向屈曲后臨界桿長減小了14%～22%，對于架空線路工程中此類水平材設計的影響十分顯著，建議受彎承載力計算時考慮橫向屈曲的不利影響。

[1] 陳大斌，等．“十二五”期間電網工程大規格角鋼推廣應用數量及其經濟性預測分析[J]．電力建設，2012，33(2)．

[2] 余朝勝．高壓輸電線路大規格高強角鋼鐵塔應用研究[J]．電力與電工，2012，32(2)．

[3] GB 50017—2003，鋼結構設計規范[S]．

[4] ASCE/SEI 10－ 15，Design of Latticed Steel Transmission Structures [S]．

[5] 郭兵．單角鋼壓桿的屈曲及穩定計算[J]．建筑結構學報，2004，(06)．

[6] 徐震，等．中美桿塔規范角鋼穩定問題對比研究[J]．低溫建筑技術，2015，(05)．

[7] 李峰，等．輸電鐵塔設計中角鋼構件穩定計算問題的討論[J]．特種結構，2006，(02)．

[8] 徐彬，等．國內外輸電線路規范角鋼構件承載力的比較研究[J]．土木工程與管理學報，2013，(01)．

[9] R．narayanan．Axially Compressed Structures Stability and Strength[M]．Applied Science Publishers London and New York，1982．

[10] C．J．Earls．On the Notion Effective Length for Single Angle Geometric Axis Flexure[J]．Journal of Constructional Steel Research，2002，(58)．

[11] Cedric Marsh．Design of Single and Multiple Angle Columns and Beams[J]．Journal of Structural Engineering，1997，123(7)．

[12] Murray C．Temple．Design of Single－ Angle Compression Members According to the Canadian Standards[J]． Can．J．Civ．Eng，1996，(23)．

[13] DL/T 5154—2012，架空輸電線路桿塔結構設計技術規定[S]．