化繁為簡:優化我們的運算
朱勝強


解析幾何的本質特征是用代數方法研究幾何問題,就是將幾何問題轉化為代數問題來研究.這就使得許多過去看起來充滿技巧,沒有多少共性規律的問題的求解變得有章可循.
由于將幾何問題轉化為代數問題后,求解主要依賴于代數手段,因此,運算在解析幾何學習中所占分量極重,而運算的優化也顯得更為重要.下面讓我們來了解幾種較常見的優化方法.
1.合理建系
將幾何問題轉化為代數問題,一般需借助坐標系.當題中沒有給定坐標系時,則需建立坐標系.在不違反題意的前提下,適當選取坐標系,有時可以收到減少計算量的效果.
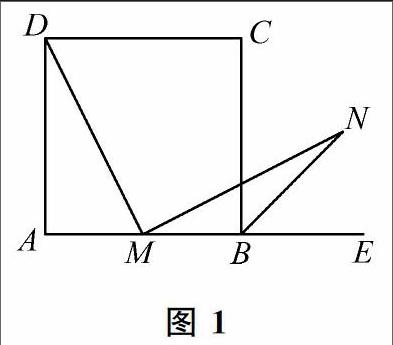
例1 如圖1,正方形ABCD中,M是以AB的中點,MN⊥MD,BN平分∠CBE,其中E在AB的延長線上,試用解析法證明:MD=MN.
證法一 如圖2,以A為坐標原點,AB所在直線為x軸,建立直角坐標系xAy.設正方形邊長為a,則A(O,0),B(a,0),D(O,a),M(a/2,o).
證法二 如果將坐標原點選為B,設正方形的邊長為a,建立如圖3所示的直角坐標系,則有D(-a,a),M(-a/2,o).
由于BN平分∠CBE,故可設N(m,m).由DM⊥MN,得kDM.kMN=-1.
從而有(a-0)/((-a-(-a/2))·(m-0)/((m-(-a/2))=-1,解得m=2.
再由兩點間距離公式,可證得MD=MN.
比較兩種不同的選取坐標系的方法,后一種運算量相對較小.事實上,在建立坐標系時,應認真觀察圖形,充分考慮圖形的一些基本特征.比如將圖形的對稱軸放在坐標軸上,對稱中心放在原點,特殊點盡可能多地放于坐標軸上等等.本題中,∠CBE的頂點相比較而言較為特殊,故放在原點,從而使角平分線條件變得更易于應用.
2.數形結合
雖然解析幾何是用代數方法來研究幾何問題,但并不排斥幾何方法在解決問題中的應用,思考問題時,若能將代數、幾何方法有機結合起來,會使原本復雜的計算變得簡潔得多.
例2 如圖4,已知點A(3,o)及圓O:x2+y2=25,以A為直角頂點作Rt△ABC,B,C在圓上.求BC的中點M的坐標滿足的關系式.
解 如圖4所示,設M(x,y),連結OC,OM,AM.在Rt△ABC中,因為M是BC的中點,所以MA=1/2BC=MC,OM⊥BC.在Rt△OCM中,MC2+OM2=0C2.所以AM2+OM2=0C2.
義因為MA2=(x-3)2+y2,OM2=x2+y2,OC2=25,
所以(x-3)2+y2+x2+y2=25.
所以點M的坐標滿足的關系式是:x2+y2-3x-8=0.
評注 這里利用了直角三角形斜邊上的中線等于斜邊長的一半及過弦中點的直徑與弦垂直等幾何性質.先發現動點的幾何特征,再將其化為代數關系,從而不必進行復雜的運算便將問題解決.
我們在初中學習過平面幾何,對直線及圓的幾何性質有一定的了解,因此,在遇到與它們有關的問題時,可以多想一想有沒有幾何方法可將問題先化簡,然后再進行必要的代數運算.
3.利用直線系方程
解析幾何中常常會遇到過兩已知直線(曲線)交點的問題.習慣的做法是先求出交點的坐標,再以此為條件作進一步思考.事實上,可用直線系方程來回避求交點,簡化計算.什么是直線系方程呢?
若l1:A1x+B1y+C1=0,l:A2x+B2y+C2=0表示的是兩條相交于點P的直線,則方程A1x+B1y+C1+λ(A2x+B2Y+C2)=o所表示的直線必定經過點P(這些直線中不包括直線l2).
例3 求過兩直線x-2y+4=0和x+y-2=0的交點,且分別滿足下列條件的直線的方程.
(1)過點A(2,1);(2)與直線3x-4y+5=0垂直.
解 (1)點A不在直線x+y-2=0上,則設所求的直線方程為(x-2y+4)+λ(x+y-2)=0.
再將(2,1)代入,可得2-2+4+λ(2+1-2)=0,解得λ=-4.
故所求直線方程為x+2y-4=0.
(2)將(1)中所設直線系方程整理為(1+λ)x+(λ-2)y+(4-2λ)=O,得此直線的斜率為k=(-1-λ)/(λ-2).
因為該直線與直線3x-4y+5=0垂直,所以-(1+λ)/(λ-2)·3/4=-1,
解得λ=11.故所求的直線方程為4x+3y-6=0.
如果將直線系中的直線改為網或其他曲線,也會得到類似的結論.
4.設而不求
在直線系方程中,我們通過合理地設直線方程,回避了求交點坐標.但有些問題中,可能需要用交點坐標來建立關系式,所以無法回避.此時可先將交點坐標設出來,但并不急于求出,只是讓其參與代數變形.有時甚至問題已經解決了,也沒有真的要求出交點坐標.這樣的簡化運算的策略稱為“設而不求”.下面我們以大家熟悉的點到直線距離公式的推導為例,看看此法的運用.
例4 求點P(x0,y0)到直線l:Ax+By+C=O的距離.
分析 如圖5,過點P作直線l1⊥l,垂足為Q,則線段PQ的長就是點P到直線l的距離.
因為l1⊥l,且過點(x0,y0),所以l1:B(x-x0)-A(y-y0)=0.
此時需注意,我們并不需要求得x,y的值,只需求得(x-x0)2和(y-y0)2的值.那么有什么簡單方法來得到它嗎?可將Ax+Bx+C=0,Bx-Ay-Bx0+Ay0=0改寫成A(x-x0)+B(y-y0)=-Ax0-By0-C,B(x-x0)-A(y-y)0=0
可以看出,設而不求的解題思路,需要在代數變形中充分關注結論的代數形式,主動地創造條件,實現條件與結論的聯通.
當然,只要我們做學習的有心人,在學習中一定會發現更多的優化運算的方法,運算是解析幾何學習乃至數學學習的不可或缺的基本功.簡化運算只能作為一種輔助手段.更重要的是在解析幾何的運算中能做到敢算、會算、善算,這樣才能真正學好解析幾何.endprint

