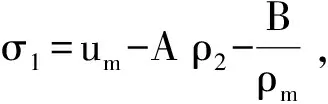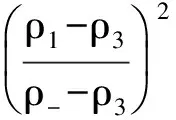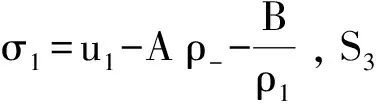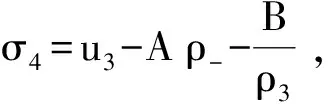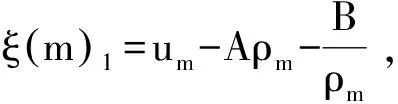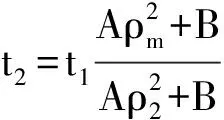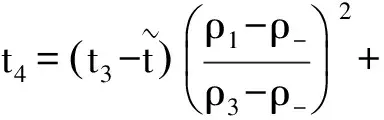修正Chaplygin氣體情形下AW-Rascle模型的Riemann問題及基本波的相互作用

王麗媛

(新疆大學(xué) 數(shù)學(xué)與系統(tǒng)科學(xué)學(xué)院，新疆 烏魯木齊 830046)

1 AW-Rascle 模型

AW-Rascle模型的方程組為

(1)

式中：u、ρ≥0、p分別表示速度、密度和壓強(qiáng). AR 模型是交通流的一個(gè)主要的流體模型，它具有較好的數(shù)學(xué)形式且廣泛用于描述交通事故及一些其它交通現(xiàn)象的形成及動力行為[1-2]. 為了抑制PW交通流模型表現(xiàn)出的氣體現(xiàn)象，2000 年，Aw和Rascle在文獻(xiàn)[3]中提出了AR模型并研究了多方氣體情形下此模型的Riemann 問題. 2009 年及2011年Sun分別在文獻(xiàn)[4]和文獻(xiàn)[5]中研究了在不包含真空和包含真空的情形下此模型基本波的相互作用.

本文研究修正Chaplygin 氣體

(2)

情形下方程組(1)的Rieman問題及基本波的相互作用. 修正Chaplygin氣體是多方氣體和Chaplygin氣體的一個(gè)線性組合，當(dāng)A=0，B=1時(shí)，式(2) 即為通常所說的Chaplygin氣體，它不僅是動力系統(tǒng)中具有負(fù)壓的等熵氣體的一個(gè)很好的數(shù)學(xué)表達(dá)，而且還可以描述一些宇宙中的暗能量模型 (參見文獻(xiàn)[6]).

2 方程組(1)和(2)Riemann問題的解

本文討論方程組(1)和(2)帶如下初始條件

ρ,u0,x=ρ±u±,±x>0

(3)

的Riemann 問題的解.

方程組(1)的特征根及對應(yīng)的右特征向量分別為

(4)

若ρ≠0，則λ1·r1≠0，λ2·r2≡0，故λ1真正非線性，λ2線性退化. 給定左狀態(tài)(ρ-,u-)，尋找其自相似解ρ,ut,x=ρ,uξ，ξ=x/t. 方程組(1)和Riemann 初值(2)在自相似的變換下化為

(5)

對于光滑解，方程組(5)的解或者為常狀態(tài)，即ρ,uξ恒為常數(shù)，或者為奇解，即

(6)

給定左狀態(tài)(ρ-,u-)，相平面上的疏散波曲線是所有可以從右邊用一個(gè)1-疏散波連接到左狀態(tài)的狀態(tài)組成的集合, 1-疏散波具有以下形式

(7)

對于間斷解, Rankine-Hugoniot 條件為

(8)

式中：ρ=ρ-ρ-；σ為間斷的速度. 由Lax熵條件有ρ-<ρ+，因此給定左狀態(tài)ρ-,u-，相平面上的激波曲線是所有可以從右邊用一個(gè)1-激波連接到左狀態(tài)的狀態(tài)組成的集合，1-激波有以下形式

(9)

因λ2線性退化，因此相平面上的接觸間斷曲線是所有可以從右邊用接觸間斷連接到左狀態(tài)的狀態(tài)組成的集合，接觸間斷表示為

Jρ-,u-：ω=u=u-

(10)

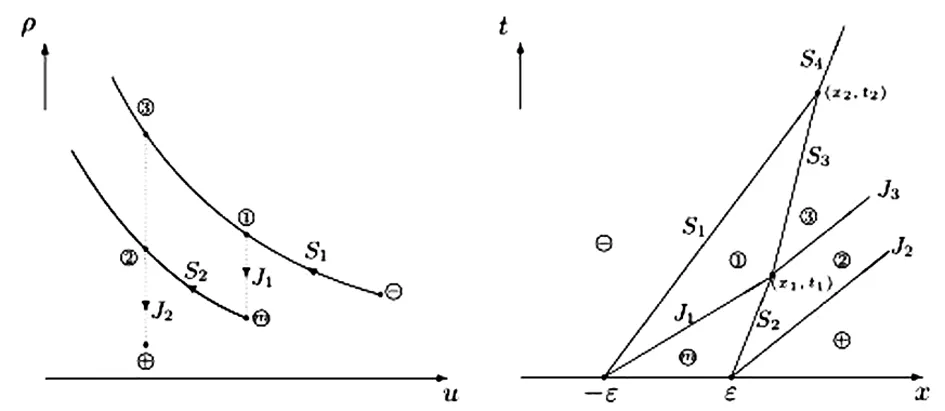
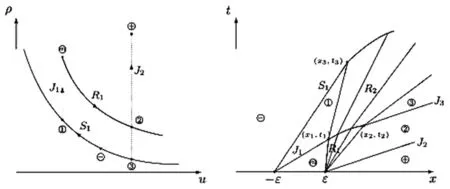
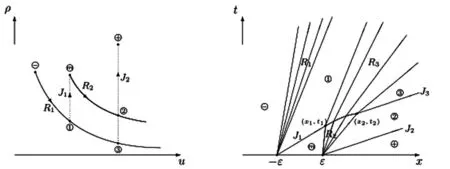
如圖1所示，ρ>0，給定左狀態(tài)ρ-,u-，過ρ-,u-畫出曲線(7)，(9)和(10)，這些曲線將相平面劃分為兩個(gè)區(qū)域：I=ρ,u|uu-. 當(dāng)右狀態(tài)ρ+,u+∈I∪II時(shí)，方程組(1)-(2)的解如下：

(1)ρ+,u+∈Iρ-,u-：R+J；

(2)ρ+,u+∈IIρ-,u-：S+J．

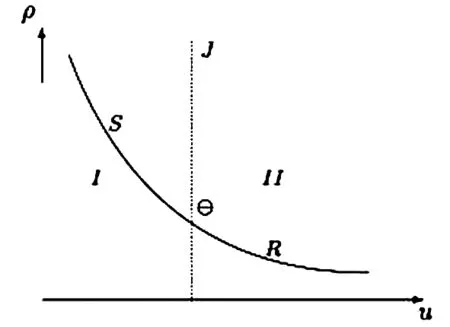
圖1 相平面和基本波曲線Fig.1 The phase plane and elementary wave curves

3 基本波的相互作用

考慮方程組(1)和(2)帶如下擾動初值

(11)

的基本波的相互作用，其中ε>0任意小. 下面我們分情況討論4種基本波的相互作用，

情形1R+J和S+J

如圖2所示，若u±

ρ-,u-+R+ρ1,u1+J1+ρm,um+

S1+ρ2,u2+J2+ρ+,u+

(a)相平面上解的結(jié)構(gòu) (b)坐標(biāo)平面上系統(tǒng)的特征線圖2 u±

(12)

在交點(diǎn)處形成新的Riemann問題，產(chǎn)生新的激波S2和接觸間斷J3.因J3和J2的傳播速度相同，故J3和J2不發(fā)生相互作用.

(13)

當(dāng)t>t2時(shí)，激波S2：x=xt滿足

(14)

由式 (14) 易得

(15)

因此S2左偏且當(dāng)ρ→ρ3時(shí)，t→.

故若ρ3<ρ-，當(dāng)t→時(shí)，S2不能穿出R，漸近線為其解為

ρ-,u-+R+ρ3,u3+J3+ρ2,u2+

J2+ρ+,u+

ρ-,u-+S2+ρ3,u3+J3+ρ2,u2+

J2+ρ+,u+

情形2S+J和S+J

如圖3所示，若u+

ρ-,u-+S1+ρ1,u1+J1+ρm,um+

S2+ρ2,u2+J2+ρ+,u+

(a) 相平面上解的結(jié)構(gòu) (b) 坐標(biāo)平面上系統(tǒng)的特征線圖3 u+

(16)

故當(dāng)t>t2時(shí)，其解可表示為

ρ-,u-+S4+ρ3,u3+J3+ρ2,u2+

J2+ρ+,u+

情形3S+J和R+J

如圖4所示，若u±>um，當(dāng)t足夠小時(shí)，初值問題(1)，(2)和(11)的解可表示為

ρ-,u-+S1+ρ1,u1+J1+ρm,um+

R1+ρ2,u2+J2+ρ+,u+

(a) 相平面上解的結(jié)構(gòu) (b)坐標(biāo)平面上系統(tǒng)的特征線 圖4 u±>umFig.4 u±>um

(17)

當(dāng)t>t1時(shí)，接觸間斷J1：x=xt表示為

(18)

由式 (18) 易得

(19)

(20)

當(dāng)t>t1時(shí)，S1：x=xt滿足如下方程組

(21)

類似情形1 可得

(22)

故S1右偏.

若ρ3<ρ-，當(dāng)t→時(shí)，S1有漸近線：其解為

ρ-,u-+R2+ρ3,u3+J3+ρ2,u2+

J2+ρ+,u+

ρ-,u-+S1+ρ3,u3+J3+ρ2,u2+J2+

ρ+,u+

情形4R+J和R+J

如圖5所示，若u-

ρ-,u-+R1+ρ1,u1+J1+ρm,um+

R2+ρ2,u2+J2+ρ+,u+

類似情形3，J1和R2相互作用產(chǎn)生R3和J3，R1和R3不會發(fā)生相互作用. 當(dāng)t→時(shí)，解為

(a) 相平面上解的結(jié)構(gòu) (b)坐標(biāo)平面上系統(tǒng)的特征線圖5 u-

ρ-,u-+R1+ρ1,u1+R3+ρ3,u3+

J3+ρ2,u2+J2+ρ+,u+

注：令擾動參數(shù)ε趨于零，交點(diǎn)將趨于原點(diǎn). 研究解的極限，進(jìn)一步將解的極限與Riemann解相比較，從而證明了Riemann 解的穩(wěn)定性.

[1]GREENBER J M, KLAR A, RASCLE M. Congestion on multilane highways[J]. SIAM Journal Applied Mathermatics, 2003, 63: 818-833.

[2]GARAVELLO M, PICCOLI B. Traffic flow on a road network using the Aw-Rascle model[J]. Communications in Partial Differential Equations, 2006, 31: 243-275.

[3]AW A, RASCLE M. Resurrection of 'second order' models of traffic flow[J]. SIAM Journal Applied Mathermatics, 2000, 60: 918-938.

[4]SUN M N. Interactions of elementary waves for the Aw-Rascle model[J]. SIAM Journal Applied Mathermatics, 2009, 69: 1 542-1 558.

[5]SUN M N. A note on the interactions of elementary waves for the AR traffic flow model without vacuum[J]. Acta Mathematica Scientia, 2011, 31: 1 503-1 512.

[6]CHAPLYGIN S A. On gas jets[J]. Scientific Memoirs, Moscow University Mathematic Physics, 1904, 21: 1-121.