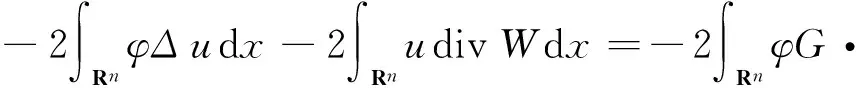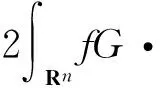Laplace方程在Lorentz-Sobolev空間上的估計
何少勇, 陳杰誠
(浙江師范大學 數理與信息工程學院,浙江 金華 321004)
0 引 言
設u是以下二維橢圓方程的解:
由奇異積分理論知,Riesz變換在L1(R2)上不是有界的,當h∈L1(R2)時,一般并不能推出u∈C0;但是,如果h可以分解成下面的形式:
h=
其中,f,g∈W1,2(R2),那么有Wente不等式[1]
‖u‖C0+‖u‖2≤C‖f‖2‖g‖2.
Bethuel[2]用對偶的方法證明了
‖u‖2≤C‖f‖L2,∞‖g‖L2.
(1)
這些不等式在偏微分方程的許多問題中起著重要的作用,具體可參閱文獻[3-5].
在Wente不等式中最關鍵的是基于以下事實[6]:
‖f⊥g‖H1≤C‖f‖2‖g‖2.
(2)
Coifman[7]指出,Hardy空間在研究偏微分方程解的正則性中起著重要作用,自此,很多學者致力于研究h在怎樣的分解形式下使得h∈H1.
‖G·f‖H1≤C‖f‖p‖G‖q.
(3)
則G·f∈H1.
本文將他們的結果推廣為如下更廣泛的形式:
定理1若f∈Lp1,q1(Rn),G∈Lp2,q2(Rn),在緩增分布意義下divG≡0,其中
則G·f∈Hr(Rn).進一步
‖G·f‖Hr≤C‖f‖Lp1,q1‖G‖Lp2,q2.
定理1中r可以小于1,從而推廣了文獻[8-9]中的結果.本文的證明依賴于極大算子在Lorentz空間上的有界性.
事實上,當r=1時,divG并不需要消失性,還可得到如下結果:
定理2如果f∈Lp1,q1(Rn),f∈Lp1,q1(Rn),G∈Lp2,q2(Rn)n,divG∈Lp2,q2(Rn),其中
那么div (fG)∈H1(Rn).進一步
‖div(fG)‖H1≤C(‖f‖Lp1,q1‖G‖Lp2,q2+‖f‖Lp1,q1‖divG‖Lp2,q2).
顯然,這個結果包含了文獻[8-9]中divG=0的特殊情形.對一般的r<1,這個結論不一定正確.
作為定理1的應用,得到下面的定理:
定理3如果u是以下橢圓方程的解:
在緩增分布意義下divG≡0,那么對于1 ‖u‖Lp,q≤C‖f‖BMO‖G‖Lp,q. 在定理3中,若取p=q=2,則‖u‖L2≤C‖f‖BMO‖G‖L2.根據一個重要的事實‖f‖BMO≤C‖f‖Ln,∞,容易看出定理2改進了一般化的Bethuel型不等式. 為方便起見,本文中出現的C表示可能依賴于pi,qi,n的正常數,在不同地方可能取不同的值. 首先介紹Hardy空間和Lorentz空間的基本定義及要用到的引理. 定義1[10]設0 Hardy空間Hp是由所有滿足下列性質的緩增分布f∈S′(Rn)所組成的空間: 定義2[11]當0 Lp,q(X,μ)={f∈(X,μ):‖f‖Lp,q<∞}. 其中: f*(t)=inf{λ:|{x∈Rn:|f(x)|>λ}|≤t}是(0,∞)上的非負遞減函數. 注1從Lorentz空間的定義可以看出,當p=q時,Lp,p=Lp,Lp,∞=弱Lp. 引理1[9]對s>0,定義依賴于s的極大算子Ms為 其中:M是Hardy-Littlewood極大算子;B(x,r)表示以x為中心、r為半徑的球.當p>s,0 (4) 取某一r2,使得 由式(4),并應用H?lder不等式和Sobolev嵌入定理得 CMr1(f)(x)Mr2G(x). (5) 因為r1 ‖G·*(G·f)‖Lr≤C‖Mr1(f)Mr2G‖Lr≤ C‖Mr1(f)‖Lp1,q1‖Mr2G‖Lp2,q2≤C‖f‖Lp1,q1‖G‖Lp2,q2. (6) 定理1證畢. (7) 對I,從定理1的證明可知 ‖I‖L1≤C‖f‖Lp1,q1‖G‖Lp2,q2. (8) 對II,由H?lder不等式得 CMr1f(x)Mr2(divG)(x). (9) 因為r1 ‖II‖L1≤C‖f‖Lp1,q1‖divG‖Lp2,q2. (10) 結合式(8)和式(10)得 C(‖f‖Lp1,q1‖G‖Lp2,q2+‖f‖Lp1,q1‖divG‖Lp2,q2). (11) 定理2證畢. 對于r<1,范數的三角不等式不一定成立,所以定理2的結論對r<1不一定成立. ‖udx. (12) 另一方面,通過Hodge分解得 V=φ+W; divW=0; ‖φ‖Lp′,q′+‖W‖Lp′,q′≤C‖V‖Lp′,q′=C. (13) 而u是以下橢圓方程的解: 其中,divG≡0.因此,利用定理1和H1-BMO對偶,結合式(12)和式(13)得 C‖f‖BMO‖G‖Lp,q‖φ‖Lp′,q′≤C‖f‖BMO‖G‖Lp,q. (14) 定理3證畢. [1]Wente H C.An existence theorem for surfaces of constant mean curvature[J].J Math Anal Appl,1969,26(2):318-344. [2]Bethuel F.A regularity result for solutions of the equation of surfaces of prescribed mean curvature[J].C R Acad Sci Paris Sr I Math,1992,314(13):1003-1007. [3]Li Jiayu,Zhu Xiangrong.Small energy compactness for approximate harmomic mappings[J].Commun Contemp Math,2011,13(5):741-763. [4]Rivière T.Conservation laws for conformally invariant variational problems[J].Invent Math,2007,168(1):1-22. [5]Zhu Xiangrong.No neck for approximate harmonic maps to the sphere[J].Nonlinear Anal,2012,75(11):4339-4345. [6]Müller S.Higher integrability of determinants and weak convergence inL1[J].J Reine Angew Math,1990,1990(412):20-34. [7]Coifman R R.Compensated compactness and Hardy spaces[J].J Math Pure Appl,1993,72(3):247-286. [8]Lemarié-Rieusset P G.A remark on the div-curl lemma[J].Studia Math,2012,210(1):77-92. [9]Zhu Xiangrong,Chen Jiecheng.Some remarks on Wente′s inequality and the Lorentz-Sobolev space[J].Appl Math J Chinese Univ,2016,31(3):355-361. [10]Stein E M.Harmonic analysis:Real-variable methods,orthogonality and ossillatory Integrals[M].Princeton:Princeton Univ Press,1993:88-91. [11]Grafakos L.Classical Fourier Analysis[M].New York:Springer,2009:44-48.1 一些定義及引理
2 定理1和定理2的證明
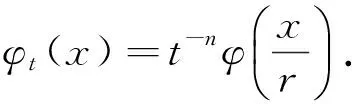

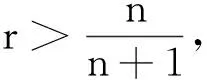
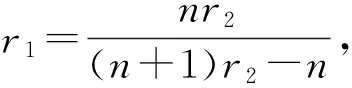
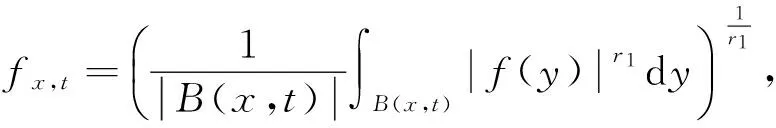
3 定理3的證明