基于數字全息術的實時光學全息顯微分辨率分析

蘇 娟, 王 輝, 吳 瓊

(浙江師范大學 信息光學研究所,浙江 金華 321004)

0 引 言

數字全息術是利用光電傳感器件記錄全息圖[1]，然后通過計算機模擬光學衍射過程來實現的被記錄物體數字再現像的過程和技術.眾所周知，光學全息技術最主要的特點是能夠三維成像.而數字全息，因為受到成像器件的分辨率限制，一般只能在微觀層面上對物體信息進行記錄和處理，很難用于宏觀物體的三維顯示.目前，數字全息的研究工作主要集中在記錄光路的設計、模擬再現像的算法和再現質量的改進上[2-5]，其在應用方面的研究涉及到實時測量、物體識別、圖像加密等領域[6-8].

由于數字全息的再現像是由計算機模擬重構的，它們通常顯示于計算屏幕上，顯然這不是光學意義上的三維顯示.利用數字全息圖實現光學三維顯示具有重要的學術和應用價值，目前這方面的研究也越來越受到重視.文獻[9]提出從數字全息圖中提取相位信息，然后利用相位空間光調制器顯示其相息圖,從而達到光學三維顯示的目的.由于需要進行相位信息的提取，故一般情況下很難進行實時顯示，同時因振幅信息的缺少也大大增加再現像的噪音;Onural 等[10]設計了一個基于數字全息的光學彩色三維視頻系統，代表著未來全息三維影視的重要發展方向，該顯示系統主要關注宏觀三維顯示的相關參數的設置，對于顯微三維顯示的特殊問題沒有給予關注；Stoykova等[11]同樣以宏觀三維顯示為目標，提出利用多個環形設置的CCD(charge-coupled device)和空間光調制器SLM(spatial light modulator)來實現宏觀場景的大視角數字全息圖的獲取和光學顯示.

本文針對基于數字全息實時光學顯微成像測量相關問題開展研究.原理是用CCD采集三維顯微物體的數字全息圖，然后將采集到的數字全息圖實時地載入空間光調制器SLM中，用激光照明SLM進行再現，對再現像的分辨率進行分析.筆者通過理論和實驗詳細研究了CCD分辨率、SLM分辨率、物體大小及再現像放大率等關鍵參量對再現像分辨率的影響，旨在為數字全息實時光學顯微再現的實際應用提供參考.

1 數字全息圖的記錄

數字全息圖的記錄原理與傳統光學全息圖原理完全相同，都是對物光波和參考光波干涉條紋記錄的過程，只不過全息圖采用了數字圖像器件記錄，因而全息圖被數字化.如圖1所示，從物體表面散射的物光波與參考光波在感光面相遇，由干涉形成的條紋光強分布被數字相機采集以數值矩陣的形式保存起來，如圖2所示.此數值矩陣所描述的圖像即為數字全息圖.

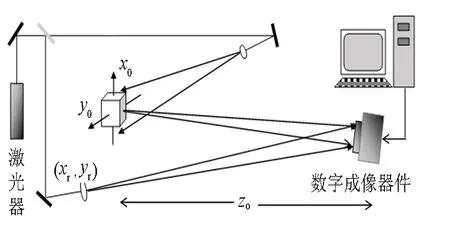
圖1 數字全息圖的記錄原理圖 圖2 成像器件結構及其參數

設記錄介質CCD靶面的物光波波前為

O(xh,yh)=O(xh,yh)exp[-jφ(xh,yh)],

(1)

參考光波波前為

R(xh,yh)=R(xh,yh)exp[-jφ(xh,yh)],

(2)

則物光波波前和參考光波波前干涉形成的光強分布為

(3)

該光強分布被成像器件記錄后得到了離散化的光強分布.設成像器件靶面的像素大小為aCCDx×aCCDy，像素間隔為dCCDx,dCCDy，感光面積為2Lhx×2Lhy，像素數為MCCD×NCCD.其中:2Lhx=NCCDdCCD，2Lhy=MCCDdCCD.則數字化全息圖可表示為[12 ]

(4)

圖3 離軸無透鏡傅里葉變換數字全息圖的記錄

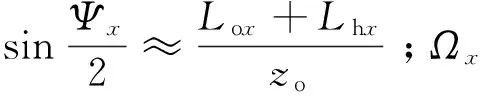
(5)

式(5)中，xr是參考光在x軸上的坐標.

2 數字全息圖的光學再現

所謂數字全息圖的光學再現指的是將光電成像器件記錄的全息圖輸入到空間光調制器中進行光學顯示.設空間光調制器像素間隔為dSLMx,dSLMy，像素數為MSLM×NSLM，像素大小為aSLMx×aSLMy.下面通過對全息圖的頻譜分析來確定光學再現像的性質.

設由式(4)表示的數字全息圖的像素與空間調制器的像素一一對應，輸入到空間光調制器后，顯示屏的振幅透射率正比于式(4).設再現時用于參考光共軛的光再現，僅考慮一維情況，則從空間光調制器出射的光復振幅分布為

(6)

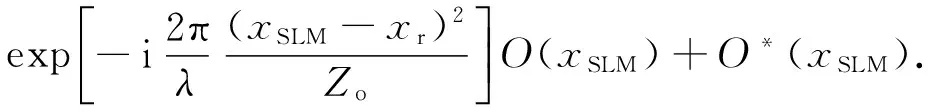
(7)

為了得到無透鏡傅里葉變換全息圖的再現像，對式(6)進行傅里葉變換,

(8)

F[IUc(xSLM)]=ZRO+R*×O+O*.

(9)

式(9)中:

(10)

ZRO是再現像的零級衍射光，R*×O和O*分別是正負一級再現像.式(8)中的梳狀函數comb(dSLM,fx)與F[IUc(xSLM)]的卷積結果形成多級像(見圖4),它是由于顯示器件像素的陣列結構引起的.

圖4 多級像譜

從圖4中可以分析出,若多級像不重疊，則可以得到對物體最大空間頻率的要求為

(11)

由圖3可以看出，物光波的邊緣光線最大空間頻率為

(12)

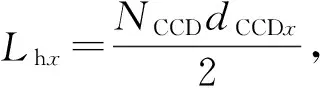
(13)

因此,若物體大小固定，則要求

(14)

把式(13)代入到式(5)，為了保證干涉條紋的分辨率不大于記錄器件的分辨率,對參考光要求為

(15)

在再現像和零級衍射光分離的條件下，對參考光的要求為

(16)

為了滿足式(15)和式(16)對參考光的要求，應該有

(17)

(18)

式(13)和式(14)可以指導數字全息光路的設計.基本原則是:如果需要關注的是再現像的分辨率，那么根據分辨率要求，利用式(13)限制物體的大小，然后根據式(14)設置物體與記錄器件的靶面距離.如果不進行這些設置和限制，那么超過記錄器件分辨率的光信息會被無效地記錄，這將會降低全息圖的信噪比，導致再現像質量下降.

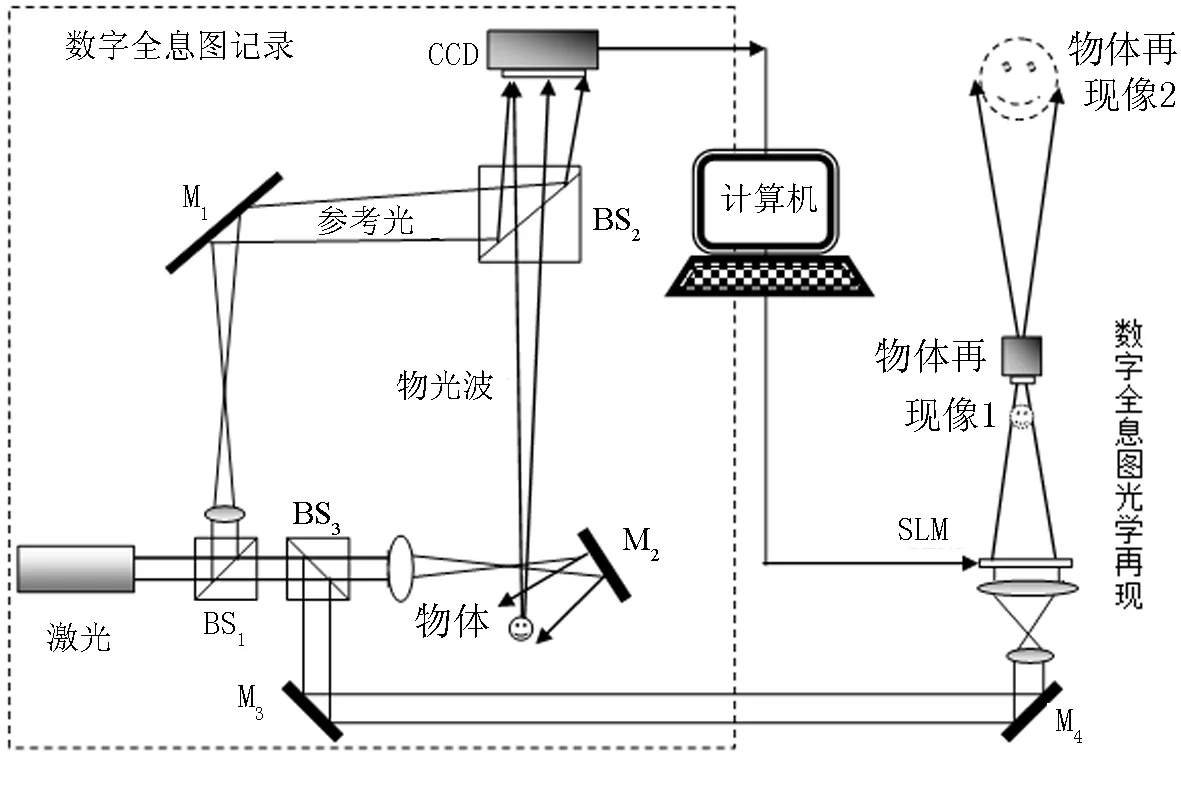
圖5 數字全息光學顯微系統光路示意圖

3 實驗系統設計及其實驗分析

本實驗的目的主要是驗證能夠記錄的物體大小與其分辨率之間的關系，即式(18).式(18)的意義為:如果希望記錄的物體大小為2Lox，那么所能記錄到的物體分辨率不大于fΩx max.

圖6 數字全息圖光學再現像照片

實驗光路如圖5所示，整個系統由2部分組成.圖5中虛框部分是數字全息圖的記錄光路.激光器發出的激光經過分光棱鏡 BS1后分為2束：其中一束經擴束后通過反射鏡M2照明樣品，由樣品反射的光形成物光O(x,y);另一束經擴束準直后作為參考光R(x,y)，經由反射鏡M1和分光棱鏡BS2入射到記錄靶面，O(x,y)與R(x,y)在靶面上干涉形成干涉條紋，最終由CCD記錄得到數字全息圖.

采用USAF 1951鑒別率板作為全息圖記錄物體.實驗時，將鑒別率板分成4個區域，它們分別是，0—7編組，2—7編組，4—7編組，6—7編組，通過光闌遮擋住不需要的部分，將4個區域分別作為記錄物體.實驗前首先測出每次編組區域的最大尺寸2Lox，然后根據式(14)調整鑒別率板與記錄靶面的距離zo.實驗中利用CCD記錄數字全息圖，其CCD的分辨率為NCCD=MCCD=2 000，像素間距為dCCDx=dCCDy=3.5×10-3mm，記錄波長為λ=0.632 8×10-3mm.

圖5虛框外部的光路是光學再現和顯微光路.由棱鏡分束器BS3分束的激光束，經由M3和M4反射鏡的反射，通過透鏡準直成為平行光照射空間光調制器SLM.由CCD記錄的數字全息圖通過計算機輸入到空間光調制器SLM，光束經SLM上的全息圖衍射后重構出實像.實驗中使用的空間光調制器SLM為振幅型的LCD(Liquid Crystal Display)，其參數為NSLM=1 920，MSLM=1 080，dSLMx=5.5×10-3mm.由CCD記錄的數字全息圖通過計算機輸入到LCD，在激光照明下可以再現出被記錄物體的實像，圖6是再現像的照片，圖7是與4個大小不同的記錄物體對應的記錄距離上全息圖的再現像,筆者逐一分析不同編組的情況.

圖7(a)是0—7編組再現像，其橫向寬度為2Lox≈12 mm，利用式(18)可以算出理論上最大分辨率為fΩx max≈13 lp/mm.根據USAF 1951鑒別率板編組號與其分辨率的關系，應該能夠分辨編組號3、元素5的單元，但從圖7(a)可以看出,實際只能分辨編組號3、元素2的單元(見圖中A點).圖7(b)是2—7編組再現像，橫向寬度為2Lox≈3.4 mm，理論分辨極限是fΩx max≈24 lp/mm.根據USAF 1951鑒別率板編組號與分辨率的關系，應該可以分辨編組號4、第4元素(B點)的像.從圖中可以看出，低于組號4、元素4的像都是比較清晰的，而高于組號4、第4元素的像都很模糊.圖7(c)是4—7編組，2Lox≈0.9 mm，理論最大分辨率fΩx max≈32 lp/mm，根據USAF 1951鑒別率板編組號與分辨率的關系可以分辨編組號5、第1元素，圖7(c)也顯示出恰好這一單元是可以被分辨的截止單元.圖7(d)是6—7編組，橫向寬度是2Lox≈0.24 mm，理論最大分辨率為fΩx max≈34 lp/mm，根據USAF 1951鑒別率板編組號與分辨率的關系知道,這一編組元素的分辨率都遠遠大于34 lp/mm，所以再現像無法分辨.

(a)Lox≈6.00 mm,zo≈421 mm (b)Lox≈1.70 mm,zo≈228 mm

(c)Lox≈0.45 mm,zo≈175 mm (d)Lox≈0.12 mm,zo≈160 mm

圖7 大小不同的記錄物體在對應不同的記錄距離上的全息圖的再現像

本文僅以實驗結果定性地證明再現物體的大小與其分辨率的制約關系，以上實驗由于光路設置存在誤差，以及光學再現激光噪音的影響，實際再現像的質量與理論有一定的差別.但總體來說實驗結果和理論分析是比較一致的，客觀的像質評價還有待進一步的研究.

4 結 論

分析了數字全息圖記錄和再現過程中影響再現像分辨率的因素.理論分析和實驗研究都證明了能夠記錄的物體大小和其分辨率之間的定量關系；并且給出了在全息圖干涉條紋空間頻率不大于記錄器件空間頻率的條件下，使再現像和零級衍射光分離的參考光的要求；同時，也給出了既能滿足記錄物體的最大分辨率又能使再現像和零級衍射光分離的最佳物距條件.對以上因素的研究，可為數字全息實時光學顯微再現的實際應用提供參考.

[1]Schnars U,Jueptner W P O.Digital recording and numerical reconstruction of holograms[J].Meas Sci Technol,2002,13(9):85-101.

[2]Qiu Peizhen,Wang Hui,Jin Hongzhen,et al.Study on the simplified phase-shifting digital holographic microscopy[J].Opt,2010,121(14):1251-1256.

[3]Ma Lihong,Wang Hui,Li Yong,et al.Partition calculation for zero-order and conjugate image removal in digital in-line holography[J].Optics Express,2012,20(2):1805-1815.

[4]Sha Bei,Liu Xuan,Ge Xiaolu,et al.Fast reconstruction of off-axis digital holograms based on digital spatial multiplexing[J].Optics Express,2014,22(19):23066-23072.

[5]Dimiduk T G,Perry R W,Fung J,et al.Random-subset fitting of digital holograms for fast three-dimensional particle tracking[J].Applied Optics,2014,53(27):177-183.

[6]Anand A,Chhaniwal V K,Javidi B.Real-time digital holographic microscopy for phase contrast 3D imaging of dynamic phenomena[J].Journal of Display Technology,2010,6(10):500-505.

[7]Christophe M,Thomas P,Gwenn C,et al.Fully automated digital holographic processing for monitoring the dynamics of a vesicle suspension under shear flow[J].Biomedical Optics Express,2014,5(5):1554-1568.

[8]Kim H,Kim D H,Lee Y.Encryption of digital hologram of 3-D object by virtual optics[J].Optics Express,2004,12(20):4912-4921.

[9]Matoba O,Naughton T J,Frauel Y,et al.Real-time three-dimensional object reconstruction by use of a phase-encoded digital hologram[J].Applied Optics,2002,41(29):6187-6192.

[10]Onural L,Yaras F,Kang H.Digital holographic three-dimensional video displays[J].Proceedings of the IEEE,2011,99(4):576-589.

[11] Stoykova E,Yaras F,Yontem A O,et al.Optical reconstruction of transparent objects with phase-only SLMs[J].Optics Express,2013,21(23):28246-28257.

[12]劉誠,朱健強.數字全息形貌測量的基本特性分析[J].強激光與粒子束,2002,14(3):328-330.