基于粒子群算法的激光位移傳感器參量優化

王曉蒙， 王會峰， 姚乃夫

(長安大學 電子與控制工程學院, 西安 710064)

引 言

激光三角測距法作為一種傳統的非接觸式光電檢測方法[1]，因其易實現、高精度、高效率以及優良的抗干擾能力和實時性等優點而被廣泛地應用在工業生產的很多領域[2]。根據激光三角測距原理可知,激光投射到被測物體表面，反射后成像于接收探測器光敏面[3],光敏面上光斑成像質量的好壞決定系統的準確性，故系統光學參量的選取至關重要。近年來，相關學者在激光三角測距傳感器的光學系統研究方面已經取得一定的成果,但在光學系統參量的獲取上仍延續著經驗選取和實驗論證的傳統方法[4],并未采用可行有效的算法，從而導致后期實驗任務冗重。

本文中對于光學系統參量選取問題，提出一種基于粒子群的優化算法。在激光三角測距傳感器數學模型的基礎上，闡明工作距、工作角、成像透鏡焦距、成像長度等參量對測量系統的影響規律,采用粒子群優化算法對參量進行優化,得到符合要求的參量值，即可縮短獲取參量時間，又可達到較高精度，為后期傳感器設計提供可靠的參考依據。

1 激光三角測距法數學模型

激光三角測距傳感器作為一種非接觸式光電檢測設備[5]，其基本原理如圖1所示。當被測物體放置在參考位置O時，激光器發射出激光通過聚光鏡，投射到被測物表面，反射后通過接收透鏡成像于電荷耦合器件(charge-coupled device，CCD)光敏面。當被測物體沿激光發射方向相對位置O移動y時，則成像于CCD接收面的光斑相對像方參考位置P移動x。x和y之間滿足透鏡成像規律。因此，通過CCD接收面得到光斑的精確位移值x，由x和y之間滿足的關系式即可得到被測物的精確位移值y，從而實現了測量待測物位移的目標。

Fig.1 Working principle and imaging model

由工作原理可知，工作距a與像距b應滿足近軸透鏡成像公式。工作角α與成像角β應滿足恒聚焦關系。則被測物的位移y與光斑位移x滿足關系式[6]：

(1)

由(1)式可得，當物體沿激光發射方向遠離激光器時，y>0mm，其最大值為可測量最遠距離，定義為ymax；當物體沿激光發射方向靠近激光器時，y<0mm，其最小值為可測量最近距離，定義為ymin，則系統的測量范圍為[ymin,ymax]。根據透鏡成像規律可知，與x向相反方向移動，故位移x與y滿足關系(2)式[7]。工作角α與成像角β滿足(3)式的恒聚焦關系[7]。

2 參量分析

2.1 接收探測器

本系統中選用的接收探測器為線陣CCD TCD1711，其有效像素數目為7450個，像素尺寸為4.7μm×4.7μm，則有效地成像長度為4.7μm×7450，即為35.015mm。

根據經驗可知，光斑若成像在CCD的邊緣位置會影響測量準確度，為了減小測量誤差，將CCD的邊緣部分有效像素舍棄，取像素數量的使用系數η=0.9，又假定測量原點在CCD中間，所以CCD成像像素空間為：(-7450×0.9/2,7450×0.9/2)，則CCD測量范圍為(-15.757mm,15.757mm)。

2.2 靈敏度

測量系統的測量靈敏度[7]為：

(4)

從(4)式可以看出，靈敏度的大小與參量(a,b,α,β,f)及被測物位移y有關。根據(4)式可以得出，靈敏度S的最小值發生在位移y取正值最大值即ymax處，把最小的靈敏度記為Smin，作為衡量測量系統精度的主要標準，在接下來的分析中提到的靈敏度均為Smin。

2.3 系統分辨力

系統分辨力由CCD兩相鄰像素中心距離大小決定，則本文中系統的分辨力為CCD中心位置的兩像素中心距離對應的被測物位移差[8]，即:

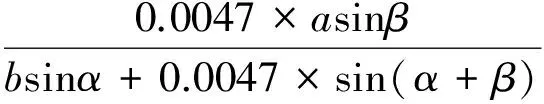
2.4 系統測量范圍

根據接收探測器CCD測量范圍可知，成像在CCD兩端的最大像點對應的被測物位移為：

(6)

由此可得系統的測量量程R=ymax-ymin。此外，系統的水平寬度L=(a+b)sinα，反映了系統體積的大小。

2.5 參量關系

2.5.1 系統指標與工作距的關系 當工作角α=30°和成像透鏡焦距f=40mm時，工作距a在(50mm，150mm)范圍內逐漸增大，可得各系統指標與工作距之間的關系，如圖2所示。

2.5.2 系統指標與工作角的關系 當工作距a=100mm和成像透鏡焦距f=40mm時，工作角α在(20°,60°)范圍內逐漸增大，可得各系統指標與工作角之間的關系，如圖3所示。

2.5.3 系統指標與成像透鏡焦距的關系 當工作距a=100mm和工作角α=30°時，成像透鏡焦距f在(20mm，60mm)范圍內逐漸增大，可得各系統指標與成像透鏡焦距之間的關系，如圖4所示。

綜合上述分析可知，接收探測器的靈敏度S與工作距的變化曲線趨勢相反，與工作角和透鏡焦距的變化趨勢相同，但對工作角及透鏡焦距取值時需考慮到實際物體體積，系統分辨能力的變化趨勢與靈敏度相同，與測量量程變化趨勢相反；水平寬度的變化趨勢則與變化量的變化趨勢完全相同，隨著工作距、工作角和透鏡焦距的變大，系統水平寬度均變大。

Fig.2 Relationship between each index and working distance

a—sensitivity b—resolution c—measurement range d—horizontal width

若使系統靈敏度和分辨力較好，根據其關系可知，工作角和透鏡焦距將取到較大值，但設計傳感器時為了操作方便，需將整個系統集成，故對工作角α和透鏡焦距f的取值不可過大。而系統分辨力的變化趨勢和測量量程相反；同時，系統水平寬度過大，則會造成系統體積過大。所以，在進行參量選取時，應根據自己實際需求，同時兼顧各個系統指標，選取合適的參量。

Fig.3 Relationship between each index and working angle

a—sensitivity b—resolution c—measurement range d—horizontal width

3 參量優化

激光三角測距傳感器的光學參量較多且相互牽制，目前大多數學者僅采用實驗方法選擇參量，參量選取精度較低，從而大大增加了后期實驗部分的工作。因此，本文中在對光學參量深入分析的基礎上采用粒子群優化算法(particle swarm optimization，PSO)，同時結合本系統所需，獲取符合要求的參量，為后期傳感器的設計提供指導依據。

Fig.4 Relationship between each index and focal length of image lens

3.1 粒子群算法-罰函數法

粒子群優化算法是一種新的進化算法[9]。首先對一群粒子進行隨機初始化，然后找到搜索空間的最優粒子并追隨，即不斷地更新迭代直到找到最優解[10]。在迭代時，粒子通過追尋兩個最優解來進行速度和位置更新，其更新公式如下所示[11]：

vij(t+1)=ω×vij(t)+c1×r1×[pij-xij(t)]+

c2×r2×[pg,j-xij(t)],

xij(t+1)=xij(t)+vij(t+1)(8)

式中,i為第i個粒子，i=1,2,…,N,其中N為粒子群的個數；j為第j維，j=1,2,…,d，其中d為粒子維數；pij為個體極值，為粒子個體本身所找到的最優解；pg,j為全局極值，為當前整個粒子群找到的最優解[12]，用于pg,j表示全局極值；t為迭代次數；ω為慣性權重；c1和c2為學習因子；r1和r2為0到1之間均勻分布的隨機數[13]。

由于本文中的激光三角測距傳感器的測量量程要求為10mm，故需在粒子群優化算法的基礎上加入測量量程的約束條件。目前罰函數法在處理約束問題時應用最廣泛，因此,本文中采用罰函數法來處理對測量量程的約束。

罰函數法所構造的廣義目標函數形式如下[14]：

F(x)=f(x)+h(k)H(x),(x∈Q?En)(9)

式中,f(x)是約束優化問題的原始目標函數；h(k)H(x)為懲罰項；h(k)為懲罰系數；H(x)是多級分配懲罰函數，Q為優化設計變量空間，E為實數集，n為優化設計變量個數。

3.2 參量優化及結果分析

基于罰函數的粒子群優化參量的計算流程如圖5所示。通過試算，確定粒子群算法的參量如下：粒子個數為20，粒子維數為3維，迭代次數為300，慣性權重[15]ω=0.6，學習因子c1=c2=1.7，初始懲罰系數h0=0.1，迭代中轉步為100，懲罰系數增大倍率m=1.4，確定參量工作距a優化空間為(50mm,150mm),工作角α的優化空間為(20°,40°)，焦距f的優化空間為(20mm，40mm)。根據(4)式定義原始目標函數：

Fig.5 Flow chart of parameter optimization

(10)

式中,β的參量關系由x1,x2,x3表示。

采用粒子群優化算法得到一組優化結果，函數迭代圖如圖6所示，所有參量結果如表1所示。

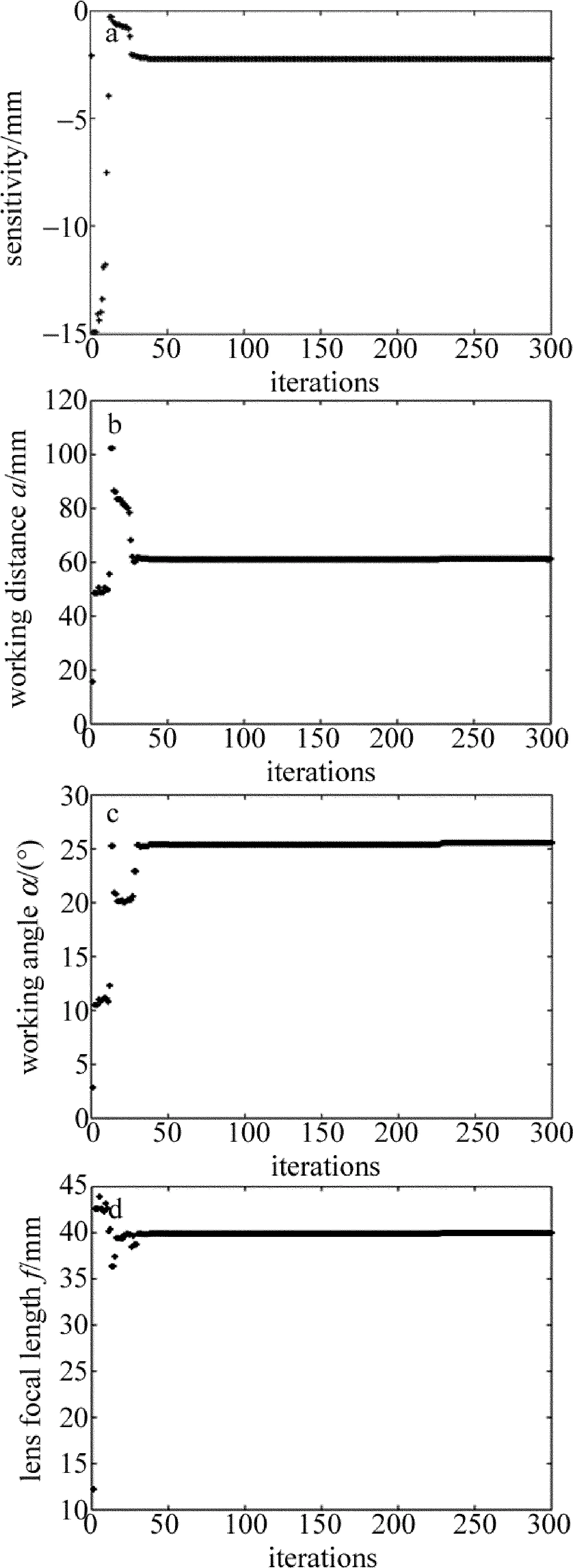
Fig.6 Function iteration graph

a—sensitivity b—working distance c—working angle d—lens focal length

Table 1 The optimized results

通過粒子群算法進行參量優化，在靈敏度最大和測量量程一定的要求下，確定粒子的搜索空間，得出滿足本系統所需的最優解。優化結果得出的最小靈敏度Smin達到2.2386mm時，系統分辨力可達2.8μm，由圖7可知，相對市場上的部分產品，利用粒子群優化得到的分辨力可達到較高水平，此時工作距a=61mm時，像距b=115mm。由于激光發射和成像部分要組裝到一起，像距過大會導致系統體積過大，因此在像距部分放置平面鏡，以光反射原理為基礎，使光斑成像在CCD接收面上，從而減小系統體積。工作角α角越大及透鏡焦距f越大，靈敏度越大，在考慮要同時兼顧靈敏度和系統體積的基礎上，取α=25°，取f=40mm，此時成像角β=14°。在所要求的搜索空間內，粒子群算法優化結果基本符合本系統要求，可作為后期實驗時的重要參考。

Fig.7 Comparison of resolution

4 結 論

從測量原理出發，對激光位移傳感器光學參量進行建模分析，并采用粒子群算法進行優化，獲取符合本系統要求的最優參量，通過MATLAB優化發現該算法在高精度高效率情況下能夠得到三角測距最優參考值，對激光三角測距法具有一定的指導意義。但整個分析實驗均為理想情況下，并未考慮器件、環境及人為等因素造成的誤差及影響。因此在進行實際測量時，需根據實際情況做適當調整，并采取相應手段盡可能消除干擾，補償器件造成的誤差。

[1] WU W，YAN L P.Laser displacement ranging system based on PSD [J].Microcontrollers & Embedded Systems,2016,16(1): 49-52(in Chinese).

[2] WANG X J, GAO J, WANG L. Survey on the laser triangulation[J]. Chinese Journal of Scientific Instrument, 2004, 25(4):601-604(in Chinese).

[3] WU J B, LUO Q M.Biomedical applications of laser triangulation [J].Laser Technology,2006,30(1):1-4(in Chinese).

[4] ZHU Y X， ZHAO J， WANG Y L. Model establishment and parameter optimization of high precision laser ranging system [J]. Machinery, 2016,54(7):68-71(in Chinese).

[5] DEMEYERE M，RURIMUNZU D，EUGENE C. Diameter measurement of spherical objects by laser triangulation inall ambulatory context[J]. IEEE Transactions on Instrumentation and Measurement,2007,56(3):867-872.

[6] JIN W Y, ZHAO H, TAO W. Modeling of laser triangulation sensor and parameters optimization [J].Chinese Journal of Sensors and Actuators, 2006, 19(4):1090-1093(in Chinese).

[7] SEN W X, FENG P, KE X,etal. Melt level measurement for the CZ crystal growth using an improved laser triangulation system [J]. Measurement, 2017,103(5):27-35.

[8] EHLERT D, HORN H J, AME R. Measuring crop biomass density by laser triangulation[J]. Computers and Electronics in Agriculture,2008,61(2):117-125.

[9] XIE Zh J, ZHENG L J, QU Zh G.Improved PSO algorithm based PID controller of permanent magnet synchronous motor [J].Modern Electronics Technique,2017,40(7):139-142(in Chinese).

[10] WANG D F, MENG L. Performance analysis and parameter selection of PSO algorithms [J].Acta Automatica Sinica,2016,40(10):1552-156(in Chinese).

[11] DAI C, WANG Y Q, XUE F. 3-D lidar echo decomposition based on particle swarm optimization [J]. Laser Technology,2016,40(2):284-287(in Chinese).

[12] RIWANTO B A, TIKKA T, KESTILA A. Particle swarm optimization with rotation axis fitting for magnetometer calibration[J].IEEE Transactions on Aerospace and Electronic Systems,2017，53(2):1009-1022.

[13] LIU Zh X, LIANG H.Parameter setting and experimental analysis of the random number in particle swarm optimization algorithm[J].Control Theory & Applications，2010，27(11):1489-1496(in Chinese).

[14] ZHANG L P, YU J H, HU Sh X. Optimal choice of parameters for particle swarm optimization[J]. Journal of Zhejiang University Science A(Science in Engineering),2005,6A(6):528-534.

[15] ZHANG G Y, WU Y J. Multi-constraint optimization algorithm based on multistage punish function and particle swarm optimization [J].Journal of Beijing Institute of Petrochemical Technology, 2008, 16(4):30-32(in Chinese).