求解VRP的一種改進模擬退火算法

李珊珊

【摘 要】建立車輛路徑問題（Vehicle Routing Problem， VRP）的數學模型，在傳統模擬退火算法的基礎上提出三方面的改進，通過算例驗證模型和改進算法的有效性。

【Abstract】The mathematical model of VRP is established， and 3 improvements are put forward on the basis of traditional simulated algorithm. The validity of the model and the improved algorithm are proved by an example.

【關鍵詞】VRP；數學模型；改進模擬退火算法

【Keywords】VRP； mathematical model； improved simulated annealing algorithm

【中圖分類號】F503 【文獻標志碼】A 【文章編號】1673-1069（2018）02-0147-02

1 引言

車輛路徑問題（Vehicle Routing Problem， VRP）由Dantzig等[1]提出后，便使運籌學理論和生產生活實際聯系在一起，因此很快便引起運籌學、數學、物流學、計算機應用等學科專家的廣泛關注。VRP問題的求解算法一直是國內外專家研究的重點問題，目前最主要的求解算法是啟發式算法[1]，包括：模擬退火算法、禁忌搜索算法、粒子群算法、蟻群算法和伊藤算法等。

Kirkpatrick等人發現數學中的組合優化問題和物理上固體退火過程之間所存在的相似性，于是他們把固體物理退火的思想引入組|合優化問題中，再基于Monte-Carlo迭代策略提出了模擬退火算法（Simulated Annealing， SA）。在計算過程中，SA能夠以一定的概率收斂至全局最優解，因此，SA在這種意義上說是一種全局優化算法，并善于求解高復雜度的問題，以上觀點已經在理論上被證明。SA求解效率快而且求解質量很高[2]，所以本文采用對傳統SA進行改進，并求解VRP問題。

2 VRP問題模型

VRP問題可描述為：一個配送中心，多位顧客，并且已知每位顧客的位置和需求量，用一定數量的車輛從配送中心出發，規劃車輛行駛路徑，滿足每位顧客的需求且每位顧客僅能由1輛車服務，不能超過車輛相關的約束，目標是使距離最短或者運輸費用最少[3]。

本文相關符號說明：

C：表示每輛車的最大裝載能力；

ci：表示顧客i的需求量，且max（ci）≤C（1≤i≤n）；

D：表示每輛車的最大行駛距離；

dij：表示顧客與顧客或者顧客與配送中心之間的距離；

n：表示配送過程中出現的顧客總數；

r：表示配送中心具有的車輛數；

hijk：表示車輛k從顧客i到j，經過為1，不經過為0；

gik：表示顧客i由車輛k服務，經過為1，不經過為0。

此問題數學規劃模型為：

式（1）為目標函數，表示所有配送車輛的總行駛路徑長度最短；式（2）表示每輛車的裝載能力約束；（3）表示每輛車的行駛距離約束；式（4）、（5）、（6）表示每個客戶僅能被1輛車服務1次；式（7）約束了所有車輛的起始點和終點都在配送中心；式（8）表示每輛車行駛的路徑軌跡恰好為一個簡單圈，式（9）、（10）分別為決策變量。

3 改進模擬退火算法

SA是一種隨機尋優算法，從某一較高初始溫度開始，隨著溫度參數的逐漸下降，結合概率突跳特性在解空間里隨機找尋目標函數的全局最優解[3]。

本文對傳統SA的改進包括以下三個方面：

①鄰域操作方法。傳統SA采取的鄰域操作是兩點置換法（也稱為2-swap交換法）。該方法的思想是：在每一次迭代中只交換兩個節點，這種鄰域操作方法簡單易行，但其對解空間的搜索能力不強[4]。因此在每一個溫度參數下，若要保證得到當前溫度參數下的一個優解，就需要比較長的時間對解空間進行搜索。隨著溫度參數的逐漸降低，外循環的次數增多，執行算法的時間便成倍增加，進而使得算法整體的搜索時間過長。本文將鄰域操作分為兩步：第一步先進行線路內交換，對線路內交換采用2-swap、2-opt及2-insert三種交換方法隨機協作的方式實施鄰域操作，產生一新的可行解。即基于概率論的方法來決定使用某一種具體的交換法來實施鄰域操作，這樣一來便大大增加了產生新解空間的隨機性，為算法跳出局部最優提高了可能性。第二步是在第一步線路內的節點交換產生可行解后，對產生的可行解進行線路間節點的交換，線路間節點的交換是引入Osman的λ-interchange交換思想，并規定每一溫度下鄰域操作的次數=λ，從而保證在一定的時間內，能夠獲得相對較高質量的優解。

②記憶裝置的設計。在改進SA中內嵌一個記憶數組，用來存儲各優解的值，從而構成一種具有記憶功能的SA，進而使得算法的輸出為本次搜索的最優解。

③終止準則的確定。采用混合停止準則，即當溫度低于某值時或者記憶數組連續γ次無變化時，算法終止。本文取γ=20，就能保證所獲得的值為本次計算的最優解。

4 結語

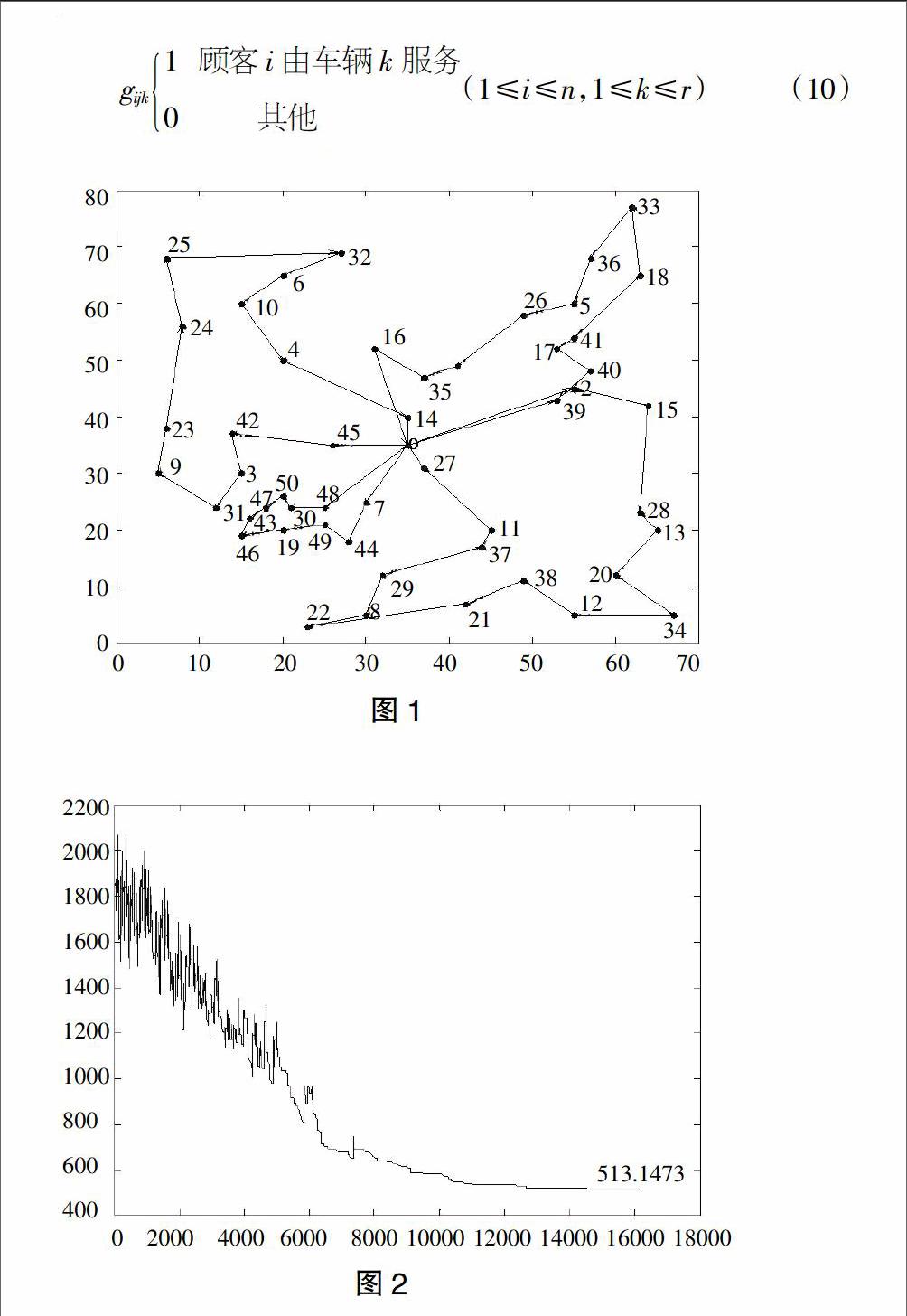
本文隨機選擇Solomon標準測試數據[5]中的R101中的50個顧客點進行了測試（如圖）。

如圖1所示，節點代表顧客的位置，線代表車輛路線，箭頭代表車輛行駛方向。圖2是增加了記憶數組存儲的每次迭代的各個解的值，記錄每次的數值，從而能夠保證最終輸出值為搜索解空間后本次計算的最優解。通過對算例進行求解，證明改進后的SA能較好的解決VRP問題，且求解質量較高，求解速度很快。

【參考文獻】

【1】Dantzig GB， Ramser JH. The truck dispatching problem[J]. Management Science， 1959， 6（1）： 80-91.

【2】辛振銘. 一種改進的模擬退火算法在TSP問題中的研究與應用[D].長春：東北師范大學，2010.

【3】K. Lund， O. B. C. Madsen， and J.M. Rygaard， Vehicle routing problems with varying degrees of dynamism. Technical report， Institute of Mathematical Modelling， Technical University of Denmark，1996.

【4】Chen， H.K.， Hsueh， C.F.， Chang， M.S. The real-time time-dependent vehicle routing problem[J]. Transportation Research Part E ，2006.42（5）：383-408.

【5】Solomon，M.M. Algorithms for the vehicle routing and scheduling problems with time window constraints[J].Operations Research ，1987.35（2）：254-265.endprint