機械臂神經網絡非奇異快速終端滑模控制

吳愛國 劉海亭 董 娜

(天津大學電氣自動化與信息工程學院， 天津 300072)

0 引言

近些年來，機械臂在自動化領域發揮著重要的作用。隨著現代工業的快速發展，它們已經被廣泛應用于眾多領域，其中許多任務需要高速度和高精度的軌跡跟蹤控制。然而機械臂的動力學模型普遍存在許多不確定性和外部擾動，難以建立精確數學模型，給機械臂的精確控制帶來一定的困難，所以研究機械臂高速度、高精度的軌跡跟蹤控制具有重要意義。

針對機械臂軌跡跟蹤控制問題已經提出了許多控制方法，比如PID控制[1]、迭代學習控制[2]、魯棒控制[3]、自適應控制[4]、反饋線性化控制[5]以及模糊控制[6]等方法，其中終端滑模控制由于其有限時間收斂特性、對參數攝動和外部擾動的強魯棒性，已被廣泛應用于機械臂軌跡跟蹤控制中。MAN等[7]首次提出終端滑模面的概念，相比線性滑模面，提高了系統在接近平衡點時的收斂速度，但該方法存在奇異性問題。為解決該問題，FENG等[8]提出非奇異終端滑模(NTSM)控制方法，并應用于機械臂軌跡跟蹤控制，證明其有效性。李升波等[9]在此基礎上提出了NFTSM控制方法，相比NTSM，提高了系統在遠離平衡點時的收斂速度，實現全局有限時間快速收斂。最近，XIAO等[10]提出了一種基于觀測器的串聯機械臂軌跡跟蹤控制方法，采用2個滑模觀測器分別估計不確定運動學和未知動力學，但其動力學觀測器是基于估計誤差的，導致該方法在實際工程中難以實現。文獻[11-12]采用RBFNN在線學習動力學建模誤差，結合自適應邊界技術估計學習誤差和外部擾動的邊界值，提高了控制精度。但以上這兩種方法都需要依賴于機械臂的模型，限制了其實際應用價值。文獻[13-14]研究了一種基于模型局部逼近的自適應終端滑模控制方法，采用RBFNN逼近被控對象模型矩陣的各個元素，實現無模型控制。但隨著機械臂自由度的增加，控制器計算量將會急劇增加，不利于系統的實時控制，并且控制律存在不連續項，容易引起抖振。GUO等[15]提出自由漂浮空間機械臂約束自適應RBF-NTSM控制方法，考慮致動器的實際物理約束，采用RBFNN補償有限的輸入，實現空間機械臂在軌操作。WANG等[16]提出了基于時延估計的機械臂連續分數階非奇異終端滑模控制方法，相比邊界層技術獲得更好的控制性能。但是該方法未考慮對估計誤差的補償，而是通過魯棒項加以抑制，這就使得所設計的控制器具有一定的保守性，需要更大的切換

控制力矩，容易引起抖振。

針對上述問題，本文提出一種基于徑向基神經網絡RBFNN的非奇異快速終端滑模(NFTSM)自適應軌跡跟蹤控制方法。

1 模型描述

基于拉格朗日方程的N關節機械臂的動力學模型表示為

(1)

M(q)——對稱正定有界慣性矩陣，M(q)∈Rn×n

G(q)——重力項矢量，G(q)∈Rn

τd——外部擾動信號，τd∈Rn

τ——控制力矩矢量，τ∈Rn

假設1：假設期望軌跡qd∈Rn是一個二次連續可微的函數。

控制目標：設計合適的控制器，使關節輸出q在有限的時間內跟蹤期望軌跡qd。

定義系統跟蹤誤差及其導數為

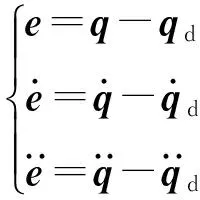
(2)

2 控制器設計

控制器的設計分為：①確定NFTSM滑模面，根據Lyapunov理論設計控制律。②設計合適的RBFNN逼近機械臂未知非線性動力學。控制系統的結構框圖如圖1所示。

圖1 控制系統結構框圖Fig.1 Block diagram of control system

2.1 控制律設計

為簡化表達式，定義

(3)

設計滑模控制系統，首先需要建立合適的滑模面，以確保產生理想的滑動模態，然后設計滑模控制律驅動系統從任意初始狀態到達滑模面。定義NFTSM滑模面為

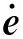
(4)

其中

α=diag(α1,α2,…,αn) (αi>0)

β=diag(β1,β2,…,βn) (βi>0)

式中r1、r2、r3、r4——正奇數，1r1/r2

李升波等[9]對式(4)進行了定量分析，從理論上證明其有限時間收斂性，本文在此只進行定性分析。當跟蹤誤差靠近平衡點時，即誤差|ei|≤1時，忽略e的高次項，式(4)近似為

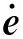
(5)

當系統處于滑模面，即s=0時，式(5)可表示為

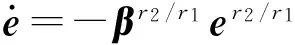
(6)

由于式(6)中e的指數小于1，則誤差導數的絕對值大于相同參數的線性滑模面，克服后者收斂速度慢的問題。

同理當跟蹤誤差遠離平衡點時，即誤差|ei|>1時，e的高次項起主要作用，此時式(4)近似為

(7)

由于式(7)中e的指數大于1，故收斂速度高于線性滑模面。

建立了合適的滑模面，下一步是設計控制律驅動系統到達該滑模面。式(4)對時間求導可得

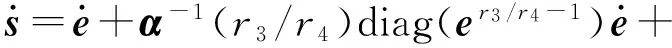
(8)

由式(1)和式(2)可知跟蹤誤差的二階導數可被重新表示為

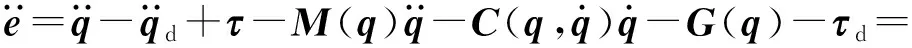
(9)

式中f——機械臂未知非線性函數

將式(9)代入式(8)，可得

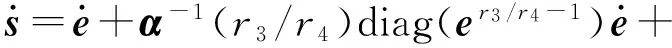
(10)

如果機械臂未知非線性函數f精確已知，可設計控制律為

τ=-f+τeq+τsmc

(11)

式中τeq——等效控制項τsmc——切換控制項

設計等效控制為

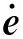
(12)

滑模控制系統利用切換控制律保證滑動模態的發生，傳統切換控制采用不連續控制項ksmcsign(s)，但需要不確定性和外部擾動的上界先驗知識。由于滑模系統只在滑動階段才對模型不確定性和外部擾動具有不變性，為加快趨近階段的速度，增強魯棒性，本文提出快速連續終端切換控制律即

τsmc=-β(r2/r1)(λ1s+λ2sr5/r6+λ3sr7/r8)

(13)

其中

r5/r6>1 0λ1=diag(λ11,λ12,…,λ1n)
λ2=diag(λ21,λ22,…,λ2n)
λ3=diag(λ31,λ32,…,λ3n)

式中λ1i、λ2i、λ3i——正常數

2.2 RBFNN設計

神經網絡具有學習和逼近任意非線性函數的能力，是控制許多復雜動力學系統的有力工具之一。相比多層感知器神經網絡，RBFNN是一種特殊的網絡結構，具有結構簡單、快速學習和更好的逼近能力，不僅可以減少神經網絡的參數調整的數目，還可以避免局部極小問題，滿足實時控制的要求。因此，為解決控制器依賴機械臂模型的問題，利用RBFNN逼近未知非線性函數。

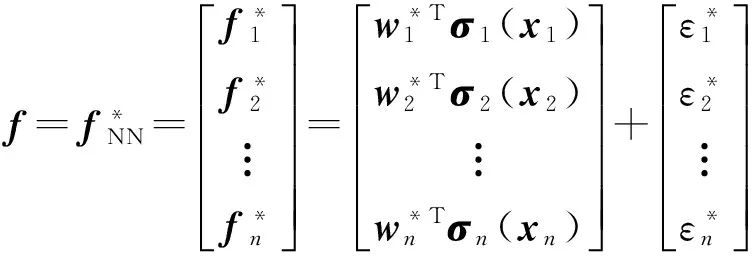
(14)

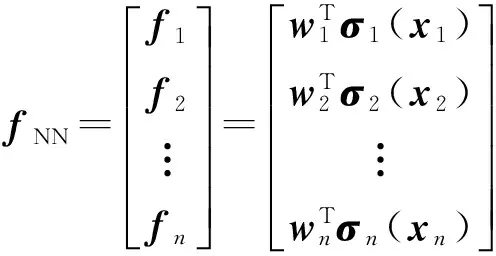
(15)

其中

wi=[wi1wi2…wiL]T

σi=[σi1σi2…σiL]T

式中fi——機械臂第i個神經網絡的實際輸出

σi——第i個神經網絡的高斯基函數

L——神經網絡隱含層的節點數

高斯基函數表達式為

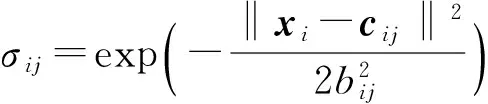
(16)

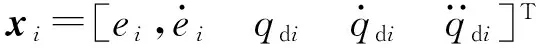
ci=[ci1ci2…ciL]
bi=[bi1bi2…biL]T

式中xi——第i個神經網絡的輸入向量

ci——第i個神經網絡的中心矩陣

bi——第i個神經網絡的基寬向量

由于神經網絡存在逼近誤差，傳統方法是增大切換增益加以抑制，但這種方法具有一定的保守性，容易引起抖振。本文設計一個神經網絡逼近誤差自適應補償項，進一步減小逼近誤差對系統的影響。

因此控制量的輸入可以被重新表示為

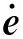
(17)

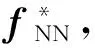
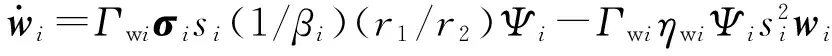
(18)

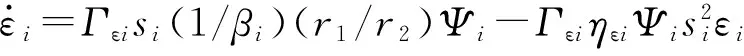
(19)

其中

式中Γwi、ηwi、Γεi、ηεi——正常數

3 穩定性分析

定理1：針對機械臂系統式(1)，當選用式(4)所示的NFTSM滑模面，式(17)的控制律和式(18)、式(19)的自適應更新律，則神經網絡的權重和誤差補償有界，閉環系統全局漸進穩定。

證明：取Lyapunov函數為

(20)

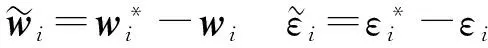
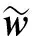
V對時間t求微分可得

(21)

將式(10)和式(17)～(19)代入到式(21)可得

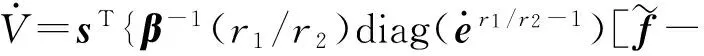
(22)

其中

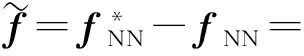
根據F-范數的性質可以得到

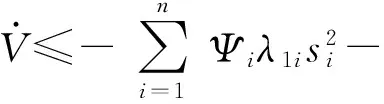
(23)

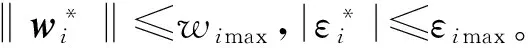
此時分以下3種情況考慮：

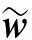
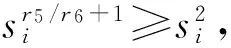
(24)

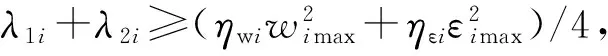
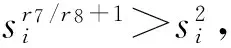
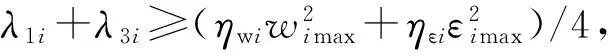
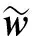
(25)

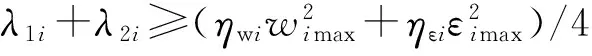
(26)

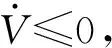
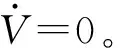
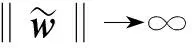
4 有限時間收斂性分析

證明：取Lyapunov函數為

(27)

Vs對時間t求微分可得

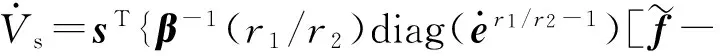
(28)

假設以下不等式成立

|ξi|≤βi(r2/r1)Kσi|si|

(29)

(30)

式中Kσi、Kεi——正常數

當滿足以下不等式時，可保證式(29)、(30)成立

(31)

(32)

由式(31)、(32)可知，取滑模函數s滿足

‖s‖≥max(Δ1,Δ2)=Δ3

(33)

將式(29)、(30)代入式(28)可得

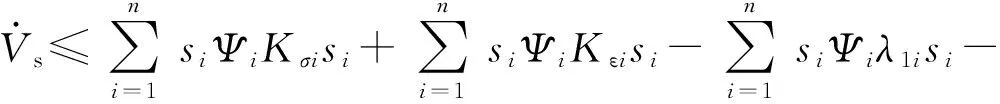
(34)

其中

λ1i>Kσi+Kεi

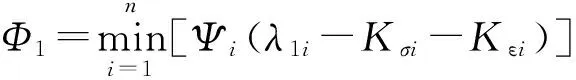
由文獻[17]可得

(35)

將式(27)、(35)代入式(34)可得

(36)

其中

υ=(r7/r8+1)/2

由文獻[17]可得有限收斂時間滿足

(37)

由式(37)可知，滑模函數s將在有限的時間內收斂到鄰域Δ3內。由式(31)、(32)可知，增大βi與r2的值或減小r1的值可使Δ3減小，Δ3越小跟蹤效果越好。

5 仿真

為了驗證本文所提的控制算法的有效性，選取6-DOF Denso 串聯機械臂的前3個關節作為控制對象，其余3個關節鎖死，并利用拉格朗日方程[18]建立該機械臂前3個關節的動力學模型，由于該模型方程比較復雜，在此沒有具體列出。通過Matlab軟件進行仿真研究，仿真采用式(17)控制律，記為NFT-T-RBF，采用式(18)、(19)自適應律，仿真參數如表1所示。

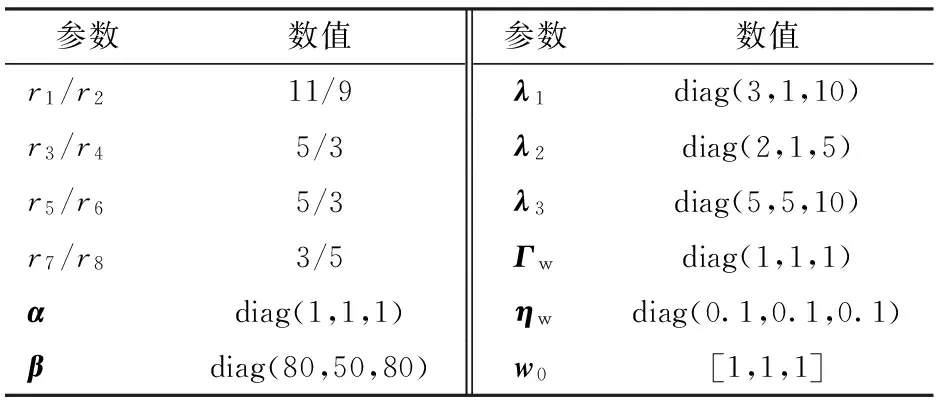
表1 NFT-T-RBF仿真參數Tab.1 Simulation parameters of NFT-T-RBF

為對比說明本文所提控制器的有效性，與以下3種控制方法的仿真結果進行對比。

控制器1：相比本文所提控制器，切換控制項采用不連續魯棒項，記為NFT-S-RBF，控制律為

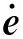
(38)

控制器1的仿真參數如表2所示。

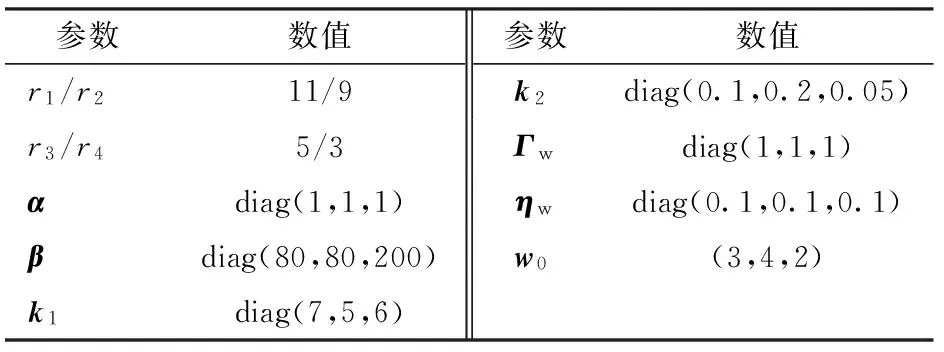
表2 NFT-S-RBF仿真參數Tab.2 Simulation parameters of NFT-S-RBF

控制器2：相比控制器1，不再引入RBF神經網絡估計系統未知非線性動力學，記為NFT-S，控制律為

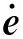
(39)

控制器2的仿真參數如表3所示。

表3 NFT-S仿真參數Tab.3 Simulation parameters of NFT-S

控制器3：相比控制器2，采用線性滑模面，記為SMC-S，該控制器的滑模面和控制律分別為

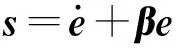
(40)

τ3=-k1s-k2sign(s)

(41)

控制器3的仿真參數如表4所示。

表4 SMC-S仿真參數Tab.4 Simulation parameters of SMC-S

機械臂3個關節的期望軌跡分別為

(42)

RBF神經網絡隱含層的節點數L=7。

為驗證所提控制算法的抗擾動性能，分別在3個關節通道的1、2、3 s時刻施加擾動，持續時間均為0.5 s，擾動值為對應關節控制量的限幅值的0.8倍，如圖2所示。圖3表示RBFNN對未知非線性函數的估計。圖4為3個關節的軌跡跟蹤曲線，期望軌跡均為正弦信號，其中前2個關節的期望軌跡的幅值為2π/3，第3個關節的幅值為5π/18。圖5為3個關節的軌跡跟蹤誤差曲線。圖6為各個關節的控制輸出力矩。由圖4和圖5可以看出，4種控制器最終都能實現軌跡跟蹤，但每個控制器的收斂速度、魯棒性等又各有不同。

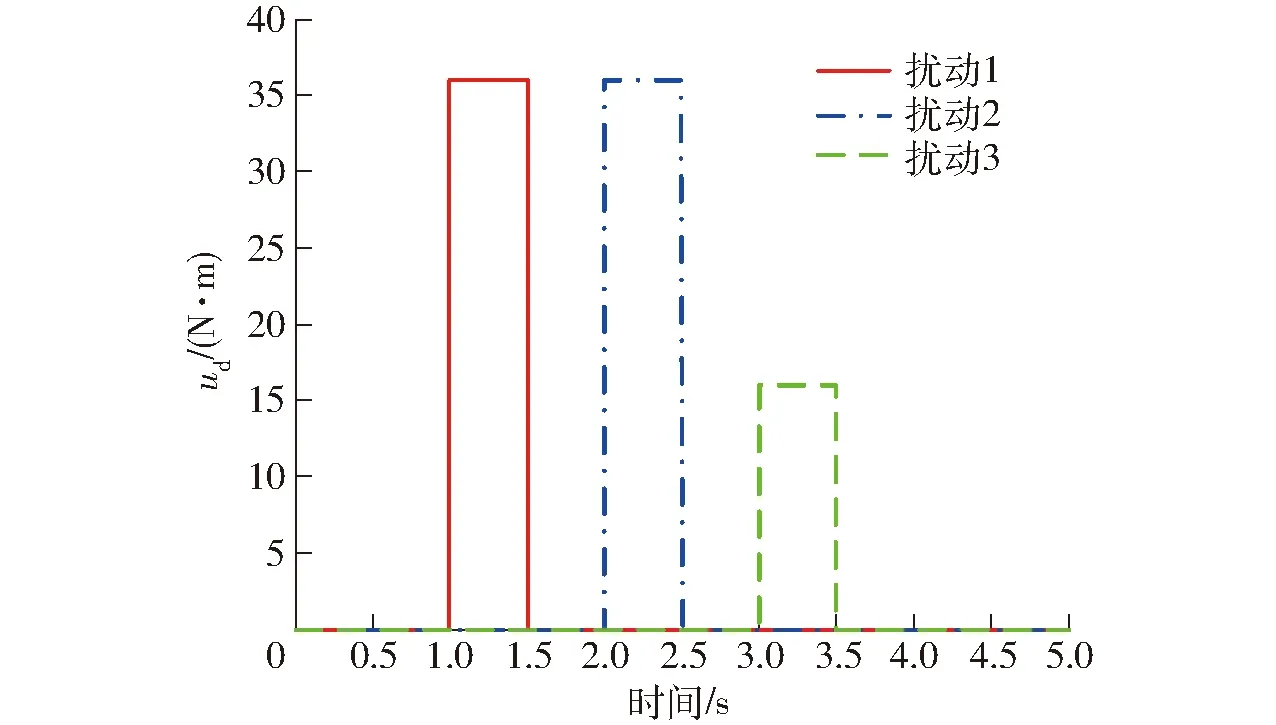
圖2 外部擾動Fig.2 External disturbance

圖3 不確定項估計Fig.3 Estimation of uncertainty

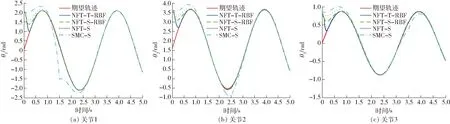
圖4 關節軌跡跟蹤曲線(仿真)Fig.4 Trajectory tracking curves of joints

圖5 關節跟蹤誤差曲線(仿真)Fig.5 Tracking error curves of joints

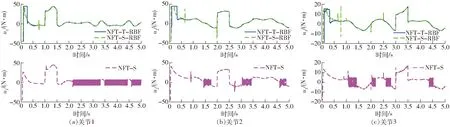
圖6 關節控制力矩(仿真)Fig.6 Control torques of joints

對比圖4、5中的NFT-S與SMC-S，兩者的主要區別是采用的滑模面不同，NFT-S控制器采用非奇異快速終端滑模面，SMC-S采用線性滑模面。由圖4可以看出，對于在1、2、3 s時刻施加的外部擾動，SMC-S控制器對擾動更為敏感。由圖5可看出，對于SMC-S控制器，外部擾動使3個關節產生的跟蹤誤差的峰值分別為1.8、0.4、0.2 rad，而對于NFT-S控制器，擾動產生的誤差均在0.1 rad以內，誤差峰值分別降低了94%、75%和50%。由圖5可以看出，SMC-S控制器的調整時間約為2 s，而NFT-S控制器的調整時間為1 s，相比前者降低了50%。以上分析表明，非奇異快速終端滑模控制方法提高了滑模運動階段的收斂速度，增強系統魯棒性。

對比控制器1與控制器2，即圖4～6中的NFT-S-RBF與NFT-S，NFT-S-RBF控制器利用RBF神經網絡對系統未知非線性函數進行實時估計和補償。由圖4和圖5可以看出，NFT-S-RBF控制器的抗擾動性能和系統收斂速度均略優于NFT-S控制器。由圖6可以看出，NFT-S控制器的控制力矩輸出產生了劇烈的抖振，這是由于切換控制項中的符號函數k2sign(s)造成的，而NFT-S-RBF控制器的輸出力矩則更為平滑。以上分析表明，引入RBF神經網絡估計系統不確定項能夠有效地削弱系統抖振。

對比本文所提控制器與控制器1，即圖4、5中的NFT-T-RBF與NFT-S-RBF，NFT-T-RBF控制器的切換控制項引入終端吸引子代替符號函數，使控制力矩輸出連續。由圖4和圖5中可以看出，NFT-T-RBF控制器的調整時間均在0.3 s以內，降低了系統響應時間，并且進一步提高系統的抗擾動性能。因此切換控制項引入終端吸引子能夠提高滑模趨近速度，增強魯棒性。

仿真結果表明，本文所提出的基于徑向基神經網絡的非奇異快速終端滑模控制方法能夠有效的提高系統控制性能，加快收斂速度，增強魯棒性，抑制系統抖振。

6 實驗

為了驗證本文所提的控制算法在實際應用中的控制性能，在Denso 6-DOF機械臂的前3個關節上進行軌跡跟蹤實驗，其余關節鎖死，該實驗平臺是Quanser公司開發的Denso 6-DOF機械臂控制系統，如圖7所示。其硬件系統主要包括Denso VP-6242G機械臂，伺服控制器，控制計算機。軟件系統為Quanser公司開發的能完全兼容Matlab的實時控制軟件Quarc，用戶可以在Simulink環境下調整內部控制器也可以獨立設計控制器，通過該軟件自動生成可執行文件。系統控制過程：編碼器測量6個關節電動機的角度位置，通過專用電纜傳送到伺服控制器的數據采集模塊，再通過以太網傳輸到計算機，通過上位機控制器計算輸出控制力矩，經數據采集模塊送到伺服驅動器，驅動機械臂關節電動機運動，完成機械臂控制任務。

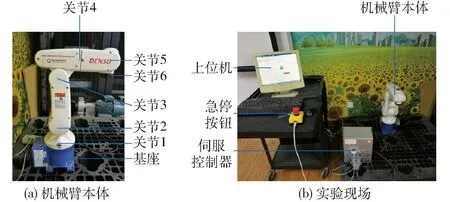
圖7 實驗平臺Fig.7 Experiment platform

機械臂控制系統的關鍵運行參數如表5所示。

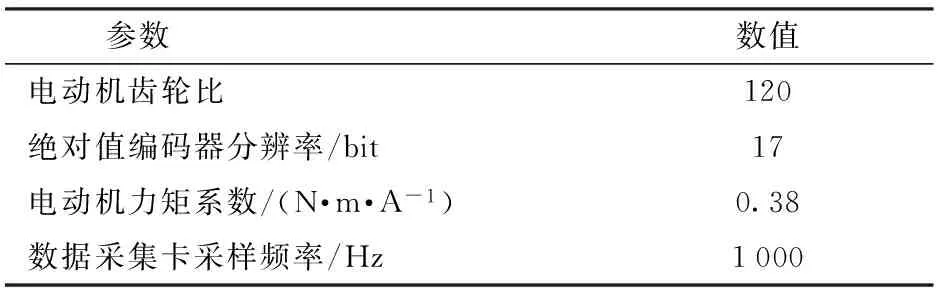
表5 關鍵運行參數Tab.5 Critical operating parameters

該實驗是依據本文所提的控制算法以及仿真研究，獨立設計控制器，實現機械臂軌跡跟蹤控制。由于實際系統中存在信號傳輸延時問題，該系統延時為6個采樣時刻，但在仿真中是不存在這種問題的，因此需要考慮系統延時對控制性能的影響，分析控制律式(17)可知，若滑模面的參數確定，其中等效控制τeq則為不可控的量。定義

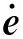
(43)

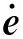
設某一次采樣時刻為t0時刻，則該時刻所需要的等效控制量為

τeq(t0)=-βΘ(t0)

(44)

然而由于傳輸延時的影響，控制量τeq(t0)將在t1時刻作用于機械臂，但t1時刻機械臂真正需要的控制量為

τeq(t1)=-βΘ(t1)

(45)

如果機械臂控制系統是漸進穩定的，則滿足

|τeq(t0)|>|τeq(t1)| (t1>t0)

(46)

這將會導致在t1時刻作用于機械臂的控制量的絕對值偏大，偏差量為

Δu=|τeq(t0)|-|τeq(t1)|=β[|Θ(t0)|-|Θ(t1)|]

(47)

偏差量Δu增大將會導致系統狀態在滑模面附近抖振，由式(47)可知，β與Δu成正比，但β與提高系統收斂速度和穩態精度也成正比，使得減小偏差量與提高系統性能相悖，為了減小每個采樣時刻的偏差量，削弱抖振，在實驗中將式(12)修改為

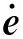
(48)

其中

φ=diag(φ1,φ2…,φn)(φi<βi)

實驗采用式(17)控制律記為NFT-T-RBF，式(18)、(19)自適應律，實驗參數如表6所示。

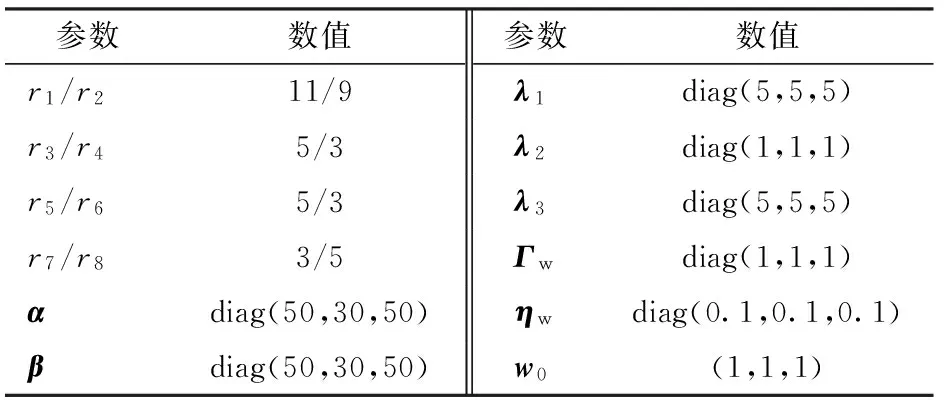
表6 NFT-T-RBF實驗參數Tab.6 Experimental parameters of NFT-T-RBF

為對比驗證本文所提控制方法的有效性，將實驗結果與WAN等[19]所提出的基于擴張狀態觀測器的滑模控制方法(PD-ESO-SMC)進行對比。PD-ESO-SMC控制方法采用擴張狀態觀測器對系統不確定項進行實時的估計和補償；滑模面采用線性滑模面，系統收斂速度慢，穩態精度低；切換控制引入sal函數，但該函數只能在滑模函數小于1時加快趨近速度，不能實現全局快速趨近。

PD-ESO-SMC方法所采用的滑模面和控制律分別為

(49)

τ=k2s+k3diag(|s|k4)sign(s)

(50)

PD-ESO-SMC方法的實驗參數如表7所示。

3個關節的期望軌跡分別為

(51)

表7 PD-ESO-SMC實驗參數Tab.7 Experimental parameters of PD-ESO-SMC

圖8為關節軌跡跟蹤曲線。圖9為關節軌跡跟蹤誤差曲線。圖10為各個關節的控制輸出力矩。圖11表示機械臂啟動的初始化時間為2.85 s，在初始化完成以后采用用戶獨立設計的控制器完成各個關節的軌跡跟蹤任務。由圖8可以看出，本文所提的控制方法比PD-ESO-SMC方法具有更快的收斂速度。由圖9可以看出，PD-ESO-SMC控制方法的誤差穩態精度在0.02 rad左右，而NFT-T-RBF控制方法的穩態精度在0.005 rad左右，顯著地提高了系統跟蹤精度。由圖10可以看出，輸出控制量有輕微的抖振，但是在允許的范圍之內。實驗結果表明，本文所提控制方法在實際應用中能夠提高系統收斂速度和跟蹤精度。

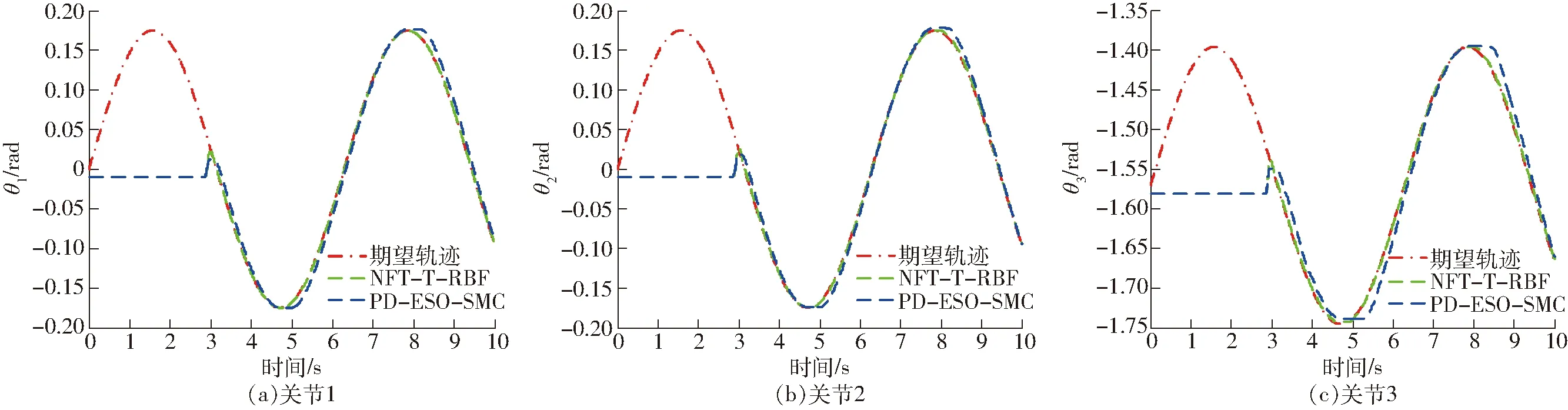
圖8 關節軌跡跟蹤曲線(實驗)Fig.8 Trajectory tracking curves of joints

圖9 關節跟蹤誤差曲線(實驗)Fig.9 Tracking error curves of joints

圖10 關節控制力矩(實驗)Fig.10 Control torques of joints

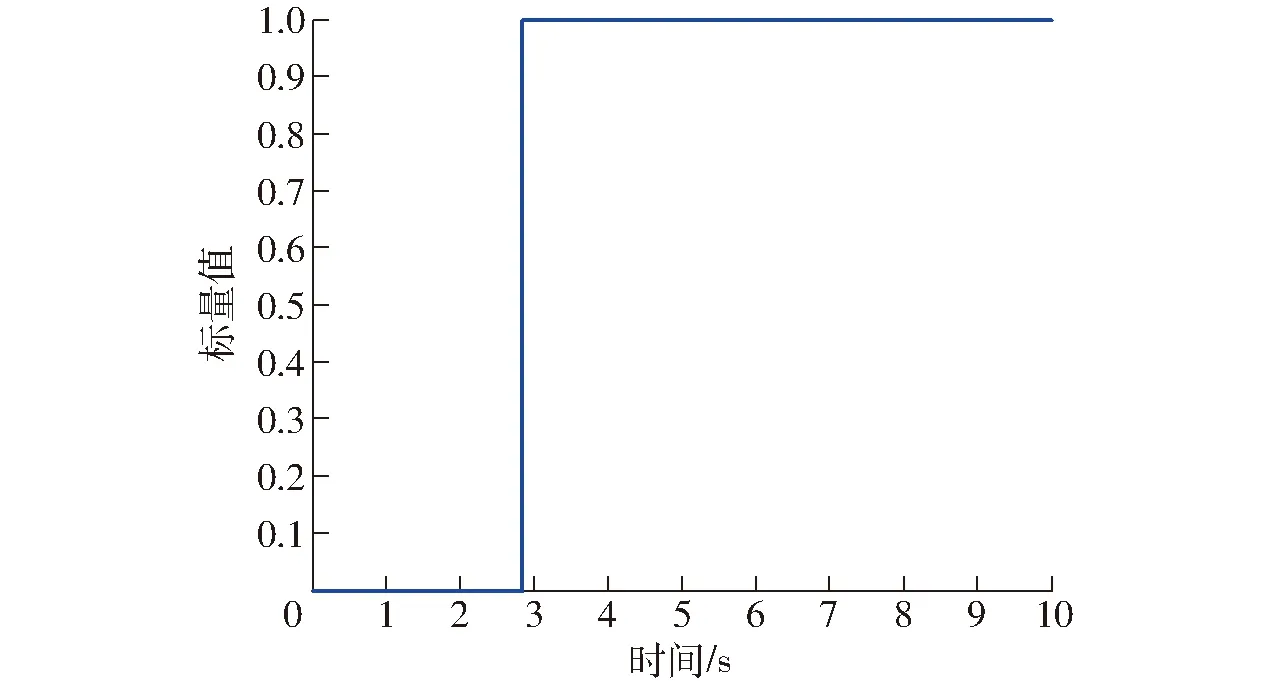
圖11 系統初始化時間Fig.11 System initialization time

為衡量整個控制系統的平均跟蹤精度，引入均方差的指標[20]比較兩者的控制性能，即

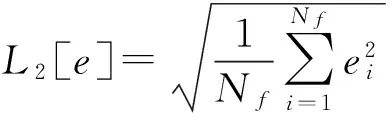
(52)

式中Nf——系統初始化完成以后的總采樣數

則系統均方差指標如表8所示。

由表8可以看出，NFT-T-RBF控制方法在3個關節的均方差比PD-ESO-SMC的均方差分別降低了51.2%、41.0%和70.3%，表明本文所提的控制方法能夠有效提高跟蹤精度。

表8 均方差Tab.8 Mean square deviation rad

7 結論

(1)針對具有不確定性和外部擾動的機械臂系統存在收斂速度慢、跟蹤精度低的問題，分析比較NFTSM和線性滑模的收斂性能，并結合RBFNN對系統未知非線性函數進行實時估計和補償，實現無模型控制，以及切換控制項引入快速連續終端吸引子，提出了一種基于RBF神經網絡的非奇異快速終端滑模控制方法，并證明了系統全局漸進穩定性和有限時間收斂特性。

(2)仿真結果表明，相比線性滑模，NFTSM使滑模運動階段收斂速度提升約50%，3個關節的擾動誤差峰值分別降低了94%、75%和50%，增強了系統魯棒性。RBFNN補償控制器在增強系統控制性能的同時有效地降低了系統抖振，使控制量輸出更平滑。快速連續終端吸引子縮短了滑模趨近階段的時間，進一步提高系統的抗擾動性能。

(3)實驗結果表明，相比PD-ESO-SMC控制方法，本文控制方法的均方差分別降低了51.2%、41.0%和70.3%，有效地提高了系統跟蹤精度。

1 ZHAO J B, WANG X Y, ZHANG G X, et al. Design and implementation of membrane controllers for trajectory tracking of nonholonomic wheeled mobile robots[J]. Integrated Computer Aided Engineering, 2015, 23(1): 15-30.

2 BOUAKRIF F, ZASADZINSKI M. Trajectory tracking control for perturbed robot manipulators using iterative learning method[J]. International Journal of Advanced Manufacturing Technology, 2016, 87:2013-2022.

3 HUANG D W, ZHAI J Y, AI W Q, et al. Disturbance observer-based robust control for trajectory tracking of wheeled mobile robots[J]. Neurocomputing, 2016, 198:74-79.

4 CUONG P V, WANG Y N. Adaptive trajectory tracking neural network control with robust compensator for robot manipulators[J]. Neural Computing and Applications, 2016, 27(2):525-536.

5 CAMBERA J C, FELIU-BATLLE V. Input-state feedback linearization control of a single-link flexible robot arm moving under gravity and joint friction[J]. Robotics & Autonomous Systems, 2017, 88:24-36.

6 FATEH M M, AZARGOSHASB S. Discrete adaptive fuzzy control for asymptotic tracking of robotic manipulators[J]. Nonlinear Dynamics, 2014, 78(3):2195-2204.

7 MAN Z H, PAPLINSKI A P, WU H R. A robust MIMO terminal sliding mode control scheme for rigid robotic manipulators [J]. IEEE Transactions on Automatic Control, 1994, 39(12):2464-2469.

8 FENG Y, YU X H, MAN Z H. Non-singular terminal sliding mode control of rigid manipulators [J]. Automatica, 2002, 38(12):2159-2167.

9 李升波, 李克強, 王建強, 等. 非奇異快速的終端滑模控制方法[J]. 信息與控制, 2009, 38(1):1-8.

LI S B, LI K Q, WANG J Q, et al. Nonsingular and fast terminal sliding mode control method[J]. Information and Control, 2009, 38(1):1-8. (in Chinese)

10 XIAO B, YIN S, KAYNAK O. Tracking control of robotic manipulators with uncertain kinematics and dynamics[J]. IEEE Transactions on Industrial Electronics, 2016, 63(10):6439-6449.

11 KUMAR N, PANWAR V, BORM J H, et al. Enhancing precision performance of trajectory tracking controller for robot manipulators using RBFNN and adaptive bound[J]. Applied Mathematics & Computation, 2014, 231:320-328.

12 YU L, FEI S, HUANG J, et al. Trajectory switching control of robotic manipulators based on RBF neural networks[J]. Circuits, Systems, and Signal Processing, 2014, 33(4):1119-1133.

13 TRAN M D, KANG H J. Adaptive terminal sliding mode control of uncertain robotic manipulators based on local approximation of a dynamic system[J]. Neurocomputing, 2017, 228:231-240.

14 PHAM C V, WANG Y N. Robust adaptive trajectory tracking sliding mode control based on neural networks for cleaning and detecting robot manipulators[J]. Journal of Intelligent & Robotic Systems, 2015, 79(1):101-114.

15 GUO S P, LI D X, MENG Y H, et al. Task space control of free-floating space robots using constrained adaptive RBF-NTSM[J]. Science China Technological Sciences, 2014, 57(4):828-837.

16 WANG Y Y, GU L Y, XU Y H, et al. Practical tracking control of robot manipulators with continuous fractional-order nonsingular terminal sliding mode[J]. IEEE Transactions on Industrial Electronics, 2016, 63(10):6194-6204.

17 YU S H, YU X H, SHIRINZADEH B, et al. Continuous infinite time control for robotic manipulators with terminal sliding mode[J]. Automatica, 2005, 41(11):1957-1964.

18 霍偉. 機器人動力學與控制[M]. 北京: 高等教育出版社, 2005.

19 WAN K G, WU A G, LIU H T, et al. Trajectory tracking of 3-DOF spatial robot manipulator[C]∥2016 12th World Congress on Intelligent Control and Automation. IEEE, 2016:3259-3264.

20 丁力, 馬瑞, 單文桃,等. 小型無人直升機航向線性自抗擾控制[J/OL]. 農業機械學報, 2017, 48(5):22-27.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20170502&flag=1.DOI:10.6041/j.issn.1000-1298.2017.05.002.

DING L, MA R, SHAN W T, et al. Linear active disturbance rejection control for yaw channel of small-scale unmanned helicopter[J/OL].Transactions of the Chinese Society for Agricultural Machinery,2017,48(5):22-27. (in Chinese)