基于無跡卡爾曼航空鋰電池的SOC估算系統

王順利，謝 非，陳 蕾，張 麗，王 露

（1.西南科技大學 信息工程學院/檢測研究所，綿陽 621010；2.西南科技大學 信息工程學院，綿陽 621010）

0 引言

當航空鋰電池處于放電情況下，電池的SOC是電池的一個重要參數，能夠清楚的表示電池的當前剩余電量，可以為電池管理系統提供控制策略依據。那么能否準確的估計電池的SOC就顯得至關重要。

國外在SOC估算方面的研究相對較成熟，美國的GregoyL.Plett考慮到電池參數存在的非線性特性，采用擴展卡爾曼濾波算法，用于SOC估算。他還提出了“sigma”點卡爾曼濾波算法，能夠更加準確地預測鋰電池組的SOC值。德國研究人員認為電池管理系統的功能應該包括均衡充電、估算電池荷電狀態以及健康狀況，并根據SOC和SOH以及電池溫度來控制電池的放電電流等。

在國內，也有大量高校、企業和科研院所對SOC估算方法進行了相關的設計研究。

鄧濤等人結合傳統的安時積分法和開路電壓法，充分考慮了電池充放電效率和電池使用溫度等因素，提出了一種帶有補償措施的基于安時積分法的SOC估算方法，使得SOC估算值的偏差在3%以內，該估算方法精確度較高，為電池SOC的在線實時估算和檢測提供了重要參考。

本文研究主從無跡卡爾曼濾波（UKF）對航空鋰電池的SOC進行估算，在simulink上建立航空鋰電池的等效電路模型，進行仿真實驗。仿真實驗表明該算法SOC估算精度誤差穩定在百分之五左右。

1 理論與方法研究

1.1 卡爾曼濾波技術研究

卡爾曼濾波是一種遞推線性最小方差估計的運算方法，該法利用系統觀測量從中提獲取所需要估算的系統狀態向量。該方法引入系統狀態向量和系統觀測向量理論，可以建立狀態方程和觀測方程，是一種最優化自回歸數據處理算法。卡爾曼濾波法用反饋控制的方法估計過程狀態。因此卡爾曼濾波法可以分為兩個部分：狀態方程和測量更新方程。

在式(1)中，k為離散時間，X（k+1）和X（k）分別為系統在k+1和k時刻的狀態，W(k)為輸入白噪聲。

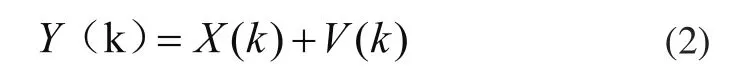
在式(2)中，k為離散時間，Y（k）為對應時刻的觀測狀態，X（k）為系統k時刻的狀態，V（k）為觀測噪聲。

由于航空鋰電池具有很強的非線性，普通的線性卡爾曼濾波算法并不能很好的保證精度。無跡卡爾曼濾波算法對非線性的系統具有良好的濾波效果。因此我們選擇了無跡卡爾曼濾波算法進行處理。

1.2 對Thevenin模型進行研究

根據對Thevenin模型的分析得到下面的式子：

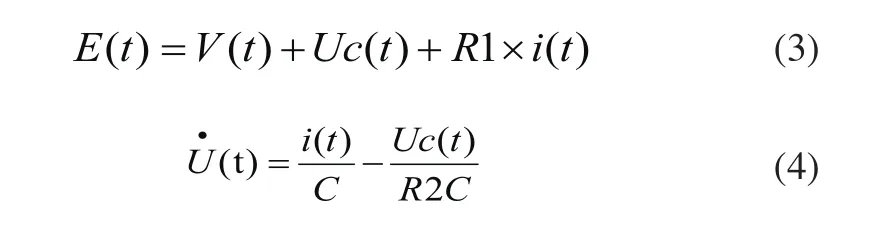
同時又因為E(t)為電源電動勢，它與SOC存在著非線性函數的關系式為E(t)=f(SOC(t))，再結合安時積分法

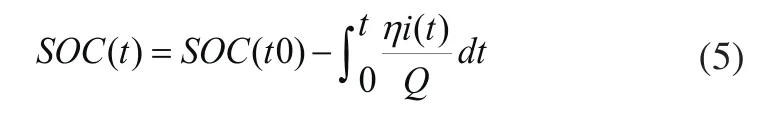
選擇SOC為系統狀態量，端電壓V（t）作為觀測量，i(t)作為系統輸入量，但由于我們這是個離散的系統，所以經過離散化處理后我們得到以下關系：

式(6)是系統狀態方程，S（k+1）和S（k）分別代表k+1以及k時刻系統的SOC值，Q是鋰電池的容量，ΔT是單位時間內（采樣時間），i（k）系統電流大小，V（k）為噪聲。

式(7)是系統測量方程，V（k）為k時刻電源電動勢的值，f（SOC(k)）為電壓與SOC之間的非線性關系，R1為歐姆內阻，i（k）為k時刻測得的電流值，Uc（k）為k時刻開路電壓值，V（k）為噪聲。

1.3 無跡卡爾曼算法研究

對于一個非線性系統來說，它的狀態方程和測量方程分別為：

k為當前所處時刻，f（XK-1，UK）為非線性系統狀態轉移方程，g（Xk-1）為非線性測量方程，Xk為狀態變量，Uk為已知的輸入，Yk為測量信號；Wk叫過程噪聲，Vk測量噪聲。我們假定Wk和Vk是不相關的均值均為零高斯白噪音，其協方差分別為Qw，Rv。具體過程如下：

1）初始值計算：

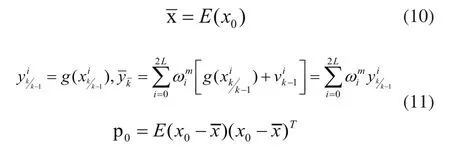
2）建立Sigma點：

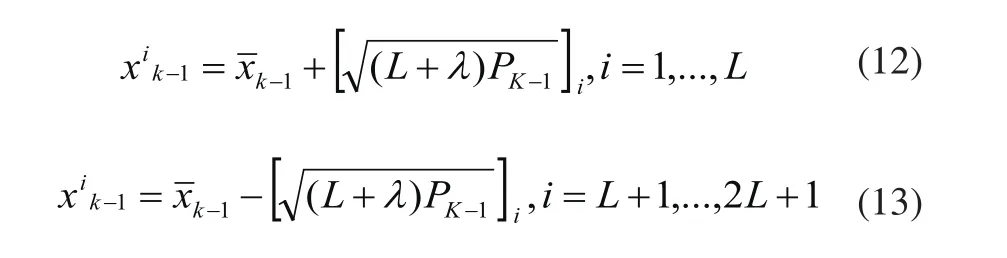
3）狀態更新方程如下：

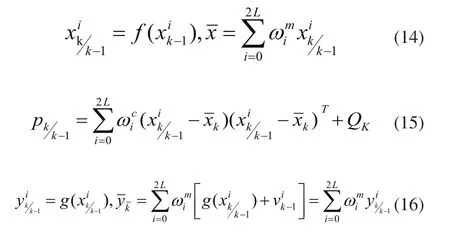
式子中的k/k-1為基于k-1時刻對k時刻的估計值。

4）測量更新方程如下：

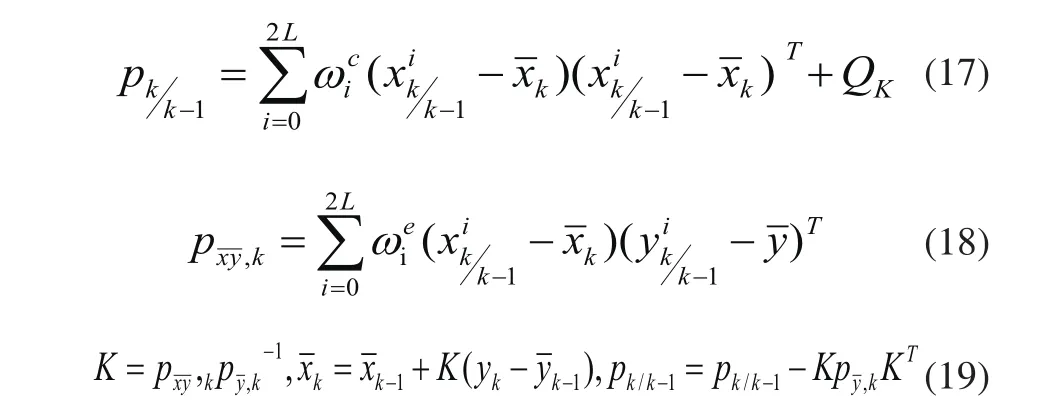
5）重復上面四個步驟。

由上述公式可知，只要給定初始條件X0和P0，根據k-1時刻的狀態值、k時刻獲得的輸入值和觀測值，就可以估算k時刻的狀態最優估計值Xk。

2 系統設計與實驗分析

2.1 電源等效電路模型的選擇

鋰電池等效電路模型的選擇對航空鋰電池的SOC估算系統來說十分重要。工程上比較常用而且易于實現的電池等效電路模型有Rint模型，RC模型，Thevenin模型和PNGV模型。Rint模型是一種理想狀態的簡單模型，U1來表示電池的開路電壓，R1來表示電池的內阻，但在實際中電池的電壓值、電流值都是隨時變動的，不是靜止不變的，故該模型誤差較大，不適合做高精度模型應用。

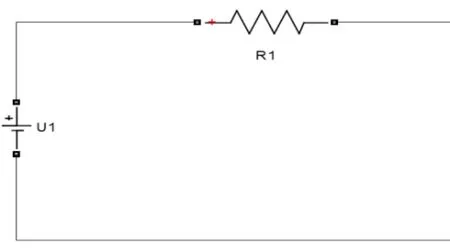
圖1 Rint模型

RC模型認為電池可由電容Cc和Cb，電阻R1、R2、Rc等效組成。Cc為一個取值非常的電容描述電池儲存的電量，Rc和Cc串聯作為儲能單元的計劃電阻；Cb表示電池極化電容；R1、R2表示電池內阻。

圖2 RC模型

Thevenin模型，該模型參數描述如下：Uc表示電池的開路電壓，R1表示電池歐姆電阻，R2表示電池極化電阻，C表示電池極化電容。

圖3 Thevenin模型

PNGV模型，該模型在Thevenin模型基礎上添加一個電容Cb，Cb表示負載電流的變化而產生的開路電壓變化也可用1/OVC表示，Ub表示電容Cb兩端的電壓。可知PNGV模型參數數學關系式：

在此，對選擇電池等效電路模型需要考慮兼顧以下三點要求：

1）模型最終是為了精確估算電池SOC值，因此需要盡可能準確的用各參數反映電池內部電壓、電流、內阻等特點；

2）電池需要適應動態充放電環境中，需要電池模型能準確的計算出電池在動態、變電流充放電電流的情況下，精確計算電池剩余電量；

3）電池模型結構盡量精簡易行，在不影響估算電池SOC精度前提下盡量精簡模型階數。

我們綜合考慮了本實驗的精度要求及模型的復雜程度，最終選擇了Thevenin模型。Thevenin模型的關系式如下：

2.2 實驗分析

圖4 soc-voc關系圖

為了驗證基于Thevenin模型的UKF算法的有效性。根據對航空鋰電池的實驗數據計算得到了電源電動勢與SOC的關系。

圖5為卡爾曼濾波系統框圖，描述了卡爾曼濾波算法的過程。

圖6為航空鋰電池電池部分的模型圖。

由圖7分析可知，卡爾曼濾波（紅色）得到的soc值非常接近于真實的soc值。達到誤差在5%之內的目標。

3 結束語

圖5 卡爾曼濾波系統框圖

圖6 電池模型

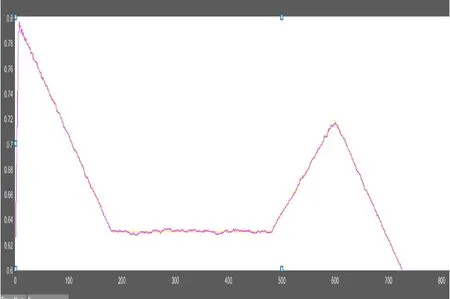
圖7 卡爾曼濾波波形圖

我們討論了關于航空鋰電池的等效電路模型及關于鋰電池的SOC的常用幾種估算方法，較為詳細的介紹了線性卡爾曼濾波及無跡卡爾曼濾波。動力電池等效模型對SOC估算具有重要意義。在建模方面，此處采用的Thevenin模型考慮了極化等因素對估算的影響，在算法上，在UKF中將比例修正法加入對稱采樣中 ，避免了局部效應問題；無跡卡爾曼在蓄電池的SOC估算系統中比擴展卡爾曼更容易實現，無跡卡爾曼并能實現更高的狀態估計精度。可以預見，基于適合的電池等效模型，無跡卡爾曼在其他各類蓄電池的估計方面也有著廣闊的應用空間，因此進一步實現基于的估算方法的工程化是很有必要的。

[1]黃小平,王巖.卡爾曼濾波原理及應用[M].電子工業出版社,2015.

[2]何志超,楊耕,盧蘭光.基于恒流外特性和SOC的電池直流內阻測試方法[J].清華大學學報,2015;55(5):532-537.

[3]Nejad S, Gladwin DT, Stone DAA systematic review of lumpedparameter equivalent circuit models for real-time estimation of lithium-ion battery states[J].Journal of Power Sources,2016,316:183-196.

[4]Barai A, Chouchelamane GH, Guo Y.A study on the impact of lithium-ion cell relaxation on electrochemical impedance spectroscopy[J].Journal of Power Sources,2015,280:74-80.

[5]Sun BX, Jiang JC, Zheng FD. Practical state of health estimation of power batteries based on Delphi method and grey relational grade analysis[J].Journal of Power Sources,2015,282:146-157.

[6]Yuan SF, Wu HJ, Ma XR. Stability analysis for li-ion battery model parameters and state of charge estimation by measurement uncertainty consideration[J].Energies,2015,8(8):7729-7751.

[7]Bazinski SJ, Wang X. Experimental study on the influence of temperature and state-of-charge on the thermophysical properties of an LFP pouch cell[J].Journal of Power Sources,2015,293:283-291.

[8]Marongiu A, Roscher M, Sauer DU. Influence of the vehicleto-grid strategy on the aging behavior of lithium battery electric vehicles[J].Applied Energy,2015,137:899-912.