基于點云數據算法的高程校準模型

(長江水利委員會 長江中游水文水資源勘測局，湖北 武漢 430010)

1 研究背景

在洪水風險圖繪制、涉河工程設計洪水計算、山洪災害分析評價等工作中，均需要獲得準確的地形高程數據，但實際往往難以實現。例如，長距離油氣管道工程可能需要穿越河流，而很多河流只有小比例尺的地形資料和少量岸上地形數據，缺乏穿越斷面實測水下地形或斷面高程數據，給穿越斷面的水位流量關系計算分析造成了不利影響；在洪水風險調查工作中一般僅進行溝道斷面測量和宅基地測量，很少開展地形測繪工作，測點數據無法保證洪水淹沒線(等高線)的準確勾繪，給風險等級評價及風險圖的準確繪制造成影響。為了解決上述問題，在現有的少量地形或高程成果數據基礎上，通過技術手段對其進行補充完善十分必要。

GoogleEarth軟件可提供全球任意區域的公開高程數據，但其平面坐標系統及高程基準和實際應用的不同，而且精度較低，尤其是絕對高程數據。本文通過相關算法，利用測區已有的少量測量數據關聯GoogleEarth的海量高程數據，進一步推求區內任意點的高程，并在此基礎上建立測區數字地面模型。

2 點云校正算法

通過七參數轉換模型可獲取GoogleEarth的平面坐標系統和實地坐標系統間的關系；通過相關下載工具(如91衛圖助手)等可獲取GoogleEarth的海量高程數據，因此，關于其平面坐標轉換和高程數據獲取問題本文不做贅述。但需說明，GoogleEarth獲取的海量高程數據并非實際測量中用到的正常高，需要進一步轉換。一般情況下，任意點的Google-Earth高程與正常高之間的高程轉換關系可用以下公式表示：

ζ=H-Hr

(1)

式中，H為GoogleEarth高程;Hr為正常高;ζ為GoogleEarth高程和正常高差值。

在測區選取同時具備GoogleEarth高程和正常高的測點, 利用二者的差值，根據高程差值與平面坐標的關系，用最小二乘法求出其高程轉換模型，再內插出測區任意點的高程差值, 從而推求出任意點的正常高。

針對目前高程擬合的研究現狀，通過兩種擬合方法的高程轉換模型即空間曲面函數法和數學曲面逼近法，實現對GoogleEarth點云數據的校正[1-5]。

2.1 空間曲面函數法

當測區已知點布設成一定區域面時，可以用空間曲面函數法求定任意點的正常高。假設測量區域內任意點的坐標為P(x，y)，GoogleEarth高程和正常高差值為ζ(x，y)，則其空間曲面函數為

(2)

式中，ai為待定參數，當測區已知點數量不小于參數個數時，可推求出參數ai，進一步求出測區任意點的GoogleEarth高程和正常高差值。

根據測區情況的不同，可選擇不同的參數轉換函數進行擬合。基于測區區域面大小，空間曲面函數法可概括為平面函數法和曲面函數法。

2.1.1 平面函數法

平面函數法即為線性內插，在小范圍區域內(本文一般為2 km以內)，可以認為GoogleEarth和正常高的起算面趨近于平面。此時，GoogleEarth高程和正常高的函數關系為

ζ(x，y)=ao+a1x+a2y

(3)

式中，ai(i=0,1,2)為未知參數，已知點的數量不少于3個。

四參數曲面函數和平面函數法類似，選用公式(2)的前3項和第5項進行擬合，函數曲面的表達式為

ζ(x，y)=ao+a1x+a2y+a3xy

(4)

式中，ai(i=0,1,2,3)為未知參數，已知點數量至少4個。

2.1.2 曲面函數法

當測區范圍較大時(本文一般為2 km以上)，為獲得高精度的轉換結果，應盡可能多的利用測區已有控制成果，求出相應的空間曲面函數。本文以6個未知函數參數為例，其曲面函數的數學模型可以表示為

ζ(x，y)=a0+a1x+a2y+a3x2+

a4xy+a5y2

(5)

若已知測區內高程差值點的個數不小于6個，則可根據最小二乘法VTPV=min求出以上未知參數ai(i=0,1,2，…，5)，由此根據公式(5)可推求出測區任意點的高程差值，再根據公式(1)即可求得任意點的正常高。

2.2 數學曲面逼近法

本文建立數學模型，用多個曲面高度逼近測量區域的高程差值，然后根據GoogleEarth高程來計算常規基準下的正常高。建立任意點和所有已知點函數關系，將這些函數的值迭加起來，獲取最佳的曲面擬合結果。根據上述思路，假設測區內任意點的坐標為P(x，y)，其高程差值為ζ(x，y)，則其數學曲面逼近法的數學模型為

(6)

式中，aj為未知參數，Q(x,y,xj,yj)為x和y的二次核函數，其中核心在(xj,yj)處，ζ可由二次式的和確定，故稱多面函數；(x，y)為高程差值待求點的坐標，(xj，yj)為高程差值已知的點的坐標。核函數一般可取[2-5]：

Q(x,y,xj,yj)=(x-xj)2+(y-yj)2+δk

(7)

式中，δ為光滑因子，k取值一般為1/2，-1/2，3/2。分別對應于以下3種類型：

正雙曲面型：

(8)

δ當其值為0時，正雙曲面退化為圓錐面。

倒雙曲面型：

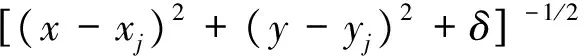
(9)

三次曲面型：

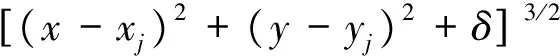
(10)

式(6)可表示為

ζ=Qa

(11)

未知參數a可根據已測點的垂直速率值按最小二乘法計算得到：

a=(QTQ)-1QTζ

(12)

于是任意點p的高程差值可求得：

ζp=Qpa=Qp(QTQ)-1QTV

(13)

再根據公式(1)便可求得任意點的正常高。

2.3 實例分析

本文以山洪災害調查工作中的一個沿河村落作為研究對象，研究區域內布設有4個控制點(G1～G4)、3個控制斷面以及相關的宅基地測量點，分布情況見圖1。

圖1 測區點位分布

由于研究區域河道長度大于2 km，本文分別采用曲面函數法和數學曲面逼近法進行高程模型的轉換，并在此基礎上進行精度分析。

(1) 沿河村落主要從4個控制點和3個斷面中選取已知點，4個控制點參與計算；選擇地勢平坦、測量精度較高的3個已知點參與計算，通過平面坐標基準轉換在GoogleEarth中讀取相應位置的GoogleEarth高程，從而完成7組同時具備Google-Earth高程和實測正常高程已知點的選擇。

(2) 分別通過曲面函數法和數學曲面逼近法計算7組已知點，求解未知參數，得到相應的高程轉換模型。

(3) 將已測量過的斷面和宅基地點分別代入2種高程轉換模型，得到其對應的正常高，利用所得的2種正常高與測量已知高程對比，來驗證兩種轉換模型的轉換精度，其精度對比如表1。

表1 部分測點兩種方法精度對比 m

從表1可以看出，兩種轉換模型都能滿足山洪災害調查測量的精度要求。總體而言，數學曲面逼近法的精度比曲面函數法的精度略高。其不足之處在于，對于地勢高差較大或者高程變化急劇時，曲面函數法精度損失較為嚴重；對于數學曲面逼近法，其核函數的選取，以及平滑因子都會對精度產生較大影響，要多次嘗試。

3 數字地面模型的建立

通過GoogleEarth點云數據校準實現了測區任意點的GoogleEarth高到正常高的改算，批量獲取研究區域內GoogleEarth點云的正常高；再利用MapGIS軟件調入點云數據，基于點云高程數據建立三角網和初設數字地面模型，并通過圖像分析系統把下載好的衛星影像轉換為MSI格式，再利用MSI文件裝入紋理文件可完成基于GoogleEarth的數字地面模型的建立，見圖2。

圖2 數字地面模型示意

4 結 語

本文提出了用空間曲面函數法和數學曲面逼近法兩種點云校正算法來實現從GoogleEarth高程到正常高的轉換。結合實例比較分析表明，空間曲面函數法和數學曲面逼近法都可滿足實際生產中的應用，但也存在其相應的局限性，實際生產中應根據測區的自然條件和已知點的分布等情況選擇合適的轉換模型；在GoogleEarth點云數據校正后可利用MapGIS軟件建立數字地面模型，實現測區高程可視化，為山洪災害調查評價或其他行業服務。

[1] 雷偉偉，鄭紅曉.二次曲面擬合法在區域似大地水準面精化中的應用[J].測繪與空間地理信息，2008，31(6)：38-42.

[2] 江在森.中國西部大地形變監測與地震預測[M].北京：地震出版社，2001.

[3] 劉萬林，王利，趙超英.GPS水準的有限元法與多面函數法的加權綜合模型[J].地球科學與環境學報，2004，26(3)：49-51.

[4] 張菊清，劉平芝.抗差趨勢面與正交多面函數結合擬合DEM數據[J].測繪學報，2008，37(4)：527-530.

[5] 黃立人，陶本藻，趙承坤.多面函數擬合在地殼垂直運動研究中的應用[J].測繪學報，2003，22(1)：25-31.