發動機懸上振動的敏感性仿真分析及應用

張志明 張繼明 王江濤

摘要：本文通過建立系統識別技術應用，對某發動機的懸置振動的敏進行激勵分析。首先利用AVL-EXOTE軟件，進行曲軸等各系統的動力學分析，得到發動機激勵力，包括缸壓、主軸軸承載荷、閥系力、活塞側向敲擊力等，然后進行征整機振動分析，輸出包括各懸上、發動機缸體等各向振動數據。通過系統識別技術應用，對各輸入的敏感性進行分析，得到主軸承座載荷最為敏感，以及該載荷到懸置振動的傳遞函數，確認支架、曲軸模態、主軸承座激勵等對懸置振動有著重要貢獻。

關鍵詞：發動機;懸上振動;系統識別;敏感度分析

引言

發動機開發中，NVH性能越來越引起大家的重視，同時發動機懸上振動作為整車振動的一個重要激勵源，不僅影響著整車舒適性，同時也會引起車內噪聲，所以在發動機NVH開發中，懸上振動的控制就顯得尤為重要。

然而發動機的工況負責，激勵較多，如各缸燃燒壓力，各主軸承座載荷，活塞側向力、閥系激勵等，要準確分析和識別懸置振動的敏感激勵，是懸上振動控制的重要內容。基于系統識別技術應用，可以快速有效識別敏感激勵，傳遞函數等，從而有效快捷的進行懸上振動改善。

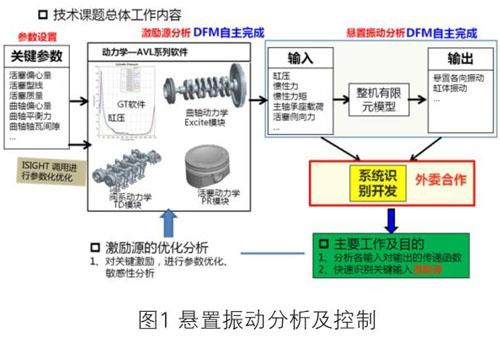
懸置振動的整體分析控制思路如圖1所示。

發動機的激勵眾多，如何快速識別發動機的敏感激勵，關鍵傳遞路徑，都成為發動機懸置振動控制的關鍵難點，如圖2所示。

本文旨在基于懸置系統識別，整機振動仿真分析，進行發動機懸置振動的預測分析，以及懸置振動敏感激勵的識別，為懸置振動的改善，提供重要的改進建議。分為以下三部分：

1.基于動力學、有限元分析的懸置振動預測。

2.利用系統識別算法，結合上述分析數據，進行輸入（激勵力）、輸出（懸置振動）之間的數學算法模型。

3.基數學模型，進行懸置振動各激勵力的敏感度分析。為懸置振動改進提供有限方向。

1 懸上振動仿真分析

基于AVL-EXCITE軟件，進行各系統動力學的分析，包括曲軸動力學、閥系動力學活塞動力學等，并將激勵力加載到整機有限元模型中，計算得到懸上振動。

1.1 多體動力學與有限元相結合的整機表面振動仿真

多體動力學（ MBD）與有限元（FEM）相結合的整機表面振動分析流程如圖3所示。缸內氣體壓力通過一維性能仿真得到。首先對發動機各運動機構進行動力學分析，得到機體受到的激勵載荷結果。然后建立整機有限元模型，并通過模態縮減法進行模型縮減，得到方便計算的整機縮減模型。最后將缸壓和發動機激勵加載到整機縮減模型上，建立整機強迫振動分析模型，得到整機振動結果。通過整機振動分析得到整機表面振動速度，進行邊界元分析，從而對發動機輻射噪聲進行分析計算^[4，5]。

整機激勵載荷分析過程說明如下：

1.缸壓激勵

發動機缸內壓力曲線可以通過一維性能仿真獲得。在有試驗樣機的情況下，通過試驗測試可以得到更為精確的缸壓激勵。

2.正時系統激勵

正時系統的激勵主要包括兩個部分：氣門落座的敲擊力、凸輪軸承對軸承座的載荷和氣門彈簧對彈簧座的激勵，正時鏈導板和張緊器的固定螺栓對缸體的激勵力。正時系統的激勵通過多體動力學仿真分析得到。

3.活塞敲擊力激勵

活塞敲擊力是在缸內爆發壓力的驅動下，活塞隨曲柄連桿機構產生的運動力去和由于問隙導致的拍擊力。為了精確計算活塞在氣缸內的運動，需要考慮活塞和缸套的輪廓以及熱變形。

4.曲軸主軸承載荷激勵

曲軸主軸承載荷是引起整機結構振動的主要激勵源。主軸承載荷不單獨計算，在進行整機振動計算時自動生成并加載在缸體軸承座對應的節點上。

整機有限元模型的建立及模態縮減是重要的一環。

整機有限元模型包括缸體、缸蓋、下缸體、油底殼、鏈殼、缸蓋罩、各個附件、變速箱殼體、懸置、進排氣歧管等。不包含曲柄連桿機構、配氣系統、前端帶系等運動件。整機有限元網格主要由實體單元和殼單元組成，主要連接螺栓用BEAM梁單元模擬。整機網格數90萬。

由于整機模型的網格數達到90萬，直接進行強迫振動分析計算量十分龐大。進行模態縮減不僅可以大大縮減計算的時間，同時能夠保證計算精度。模態縮減法基于模態綜合理論^[6]。

1.2 整機振動分析

結合動力學，有限元模型的建立，可以計算得到需求轉速、負荷下的懸置振動。論文中以5000rpm，全負荷的懸置振動輸出為例，進行系統識別及敏感性分析。

2 基于系統識別的懸置振動預測及驗證

基于以上的分析，即得到了主軸承座力、閥系激勵、活塞激勵等載荷共同作用下的懸置振動。

以激勵力作為輸入，懸上振動作為輸出，進行系統識別。

其中輸入48組，列舉主軸承座載荷、凸輪軸載荷，分別如圖5、圖6所示;輸出為懸置及缸體測點的振動等，共計21組，如圖7所示，均為時域數據。

2.1 系統識別技術應用

基于MATLAB的system identification功能，對上述輸入、輸出進行系統識別。

發動機懸上振動系統識別系統是本次測試的被測系統。該系統在MATLAB中結合系統識別工具箱（System Identification Toolhox）開發，該系統的主要功能為對給定的振動輸入輸出時程，選擇適當的系統模型進行識別。

工程應用中，通常要求戶提供的數據進行系統識別，系統的擬合度達到85%。

基于MATLAB軟件，利用simulink中system identification功能，進行系統識別程序的二次開發。分析界面如圖8所示。

該二次開發集成了數據輸入、系統識別，并支持線性、非線性等算法、求逆、敏感度分析等功能。本論文中，分析對象近似線性，故采用了線性系統識別算法，且進行了各輸入的敏感性分析。

目前關于系統識別技術原理比較成熟，如下。

（1）“線性輸入，輸出多項式模型（Linear input-output polynomial models）”是一類應用最為廣泛的多輸人多輸出線性系統模型。對與大多數線性系統都能得到較好的辨識結果。

采用算子形式，可以將輸入輸出多項式模型表示為如下的形式：

式子中，u_i（t）是第i個輸入，n_u是輸入變量的個數，y（t）是輸出，e（t）是噪聲，nk_i是第i項輸入的延遲，A、C、D、B_i、F_i是多項式，q是時移算子：q^-ny（t）=y（t-nT）。

最常用的線性輸入/輸出多項式模型是ARX模型，ARX是簡化的線性輸入輸出多項式模型，其噪聲模型具有1/A形式，噪聲與系統相互耦合，適用于使用高信噪比的數據進行識別。該模型表示為：

對于該模型，需要辨識的是多項式的系數。

（2）狀態空間模型使用狀態變量（SV）和一階差分（微分）方程組描述系統。狀態變量通過輸入輸出數據計算：

x（kT+T）=Ax（kT）+Bu（kT）+Ke（kT）

（4）

y（kT）=Cx（kT）+Du（kT）+e（kT）

（5）

x（0） =x₀

（6）

其中T是采樣周期，u（kT）是kT時間點的輸入，y（kT）是kT時間的輸出;x是一組狀態變量;A、B、C、D、K是矩陣需要識別的模型參數。

進行懸置振動的CAE預測分析時，是基于模態頻響算法，為線性分析，故本文中選擇state-spce狀態空間模型來進行識別。

2.2 算法精度驗證及效率提升

基于該算法，即實現了CAE的三維計算到O維公式算法，其精度保證，也是方法應用的重要前提。

系統識別中validation模塊，可以對預測精度進行初步確認。如圖9所示，紅線是系統是系統識別算法計算的懸置振動，與藍線有限元計算的結果幾乎重合，滿足工程應用。

同時從3維到0維算法后，計算效率大大提升，由之前的一個工況10個小時，縮短為3分鐘，為參數優化等分析提供了可行性。

3 懸置振動敏感度分析

基于MATLAB的system idenlificafion功能，對上述輸入、輸出進行系統識別。主要包括傳遞函數、貢獻度分析等，來評價各輸入的敏感性。

傳遞函數分析結果如圖10所示。橫坐標為頻率，縱坐標為為單位載荷下的振動響應。在650Hz左右，有明顯峰值，與懸置支架模態共振吻合，這也表明提高剛度，改善共振，對降低振動有著明顯的作用。

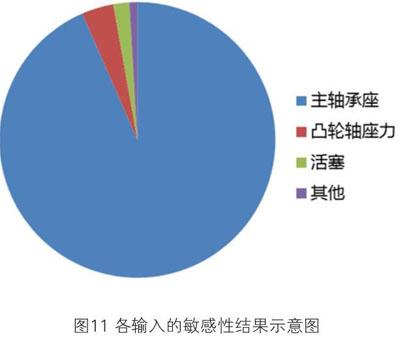
通過系統識別，可以得到各輸入的敏感性，見圖11所示，而后續懸置振動的控制，則需要結合曲軸動力學分析，進行主軸承座載荷的控制，同時盡量提高模態，來降低共振。

結合上圖可知，主軸承座載荷為懸置振動的主要激勵源，則缸壓、曲軸剛度等都是影響懸置振動的關鍵指標項，在分析中需予以管控。

4 改善效果

在機型開發中，通過曲軸剛度、懸置支架模態的提高，較好的改善了懸置振動，如圖12所示。200～800Hz懸置振動下降3～5dB左右，車內噪聲，下降1.3dB（ A）。

5 主要結論

1.建立了動力學計算激勵，在基于整機有限元模型，進行懸上振動的仿真方法。

2.建立了基于Matlab中system identification功能的系統識別程序開發，并且驗證了算法精度，滿足開發需求。

3.通過系統識別發現，主軸承座載荷是懸置振動的最敏感因素，而缸壓、曲軸的共振、懸置支架的共振均是懸置振動控制的關鍵因素。為懸置振動改進提供了重要參考。

參考文獻：

[1]徐兀，汽車發動機現代設計[M]北京：人民交通出版社，1995.

|2]榮海娜，張葛祥，金煒東等，系統辨識中支持向量機核函數及其參數的研究[J]，系統仿真學報，2006，18（11）：3204-3208.

[3]齊曉慧，田慶民，董海瑞等，基于Matlab系統辨識工具箱的系統建模[J]，兵工自動，2006，25（10）：88-90.

[4]龐劍，諶剛，何華汽車噪聲與振動一理論與應用[M]北京：北京理工大學出版社，2006

[5]舒歌群，馬維忍，梁興雨等柴油機薄壁件表面輻射噪聲的研究[J].內燃機工程，2009，30（1）：25-33.

[6]Daniela Siano， Noise Prediction of a Multi-Cylinder Engine Prototype Using Multi-Body Dynamic Simulation.SAE Technical Paper 2011， 24-0216.